GRUNDKURS EXPERIMENTALPHYSIK

Vorlesungsskript
GRUNDKURS EXPERIMENTALPHYSIK
Prof. Dr. Frank Richter
Skript angefertigt von cand. phys. Stefan Welzel
Technische Universität Chemnitz
Fakultät für Naturwissenschaften
Institut für Physik
Vorwort
VORWORT
Das vorliegende Skript basiert auf der Vorlesung in Experimentalphysik für Studenten des 1. und 2. Semesters des Diplomstudiengangs Physik. Die Vorlesung ist, anschließend an eine Einleitung, in vier große Teilbereiche gegliedert:
•
Mechanik
•
Thermodynamik
•
Elektrizitätslehre
•
Optik
Zur besseren Orientierung finden sich am Rand folgende Symbole:
!
Definitionen/Merksätze
n
Beispiele
u
Kommentare/Interpretationen/Diskussionen
SI
Definition von Einheiten nach dem SI-System
(..)
Gleichungsnummerierung
Nebenrechnung
Wird im Rahmen der Erläuterungen auf eine Gleichung aus einem vorangegangenen
Kapitel Bezug genommen, so geschieht dies durch Voranstellen der jeweiligen Kapitelnummer vor die entsprechende Gleichungsnummer (z.B. verweist die Angabe
„(11 - 6)“ auf Gl. (6) in Kapitel 11)
Desweiteren werden im Text wichtige physikalische Grundbegriffe gesondert hervorgehoben, die dann auch im Sachregister aufgelistet sind.
Weitere im Text verwendete Symbole sind:
⇒
<..>
{..}
Schlussfolgerungen
Verweis auf andere Kapitel
Quellenangabe
I
Inhaltsverzeichnis
INHALTSVERZEICHNIS
VORWORT...................................................................................................................I
INHALTSVERZEICHNIS.............................................................................................. II
A.
EINLEITUNG .................................................................................................... 1
1.
Einleitung........................................................................................................................... 2
1.1.
1.2.
1.3.
1.4.
1.5.
Was ist Physik ..................................................................................................................... 2
Die Rolle des Experimentes ................................................................................................ 2
Physikalische Modelle und Theorien .................................................................................. 4
Der „Stammbaum der Physik“ ............................................................................................ 5
Wichtige Größen und Maßeinheiten ................................................................................... 5
B.
MECHANIK ...................................................................................................... 8
2.
Kinematik........................................................................................................................... 9
2.1.
2.2.
2.3.
2.4.
2.5.
Ortsvektor............................................................................................................................ 9
Geschwindigkeit.................................................................................................................. 9
Beschleunigung ................................................................................................................. 10
Beschreibung der Kreisbewegung..................................................................................... 11
Überlagerung von Bewegungen........................................................................................ 13
3.
Dynamik ........................................................................................................................... 15
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
Trägheit ............................................................................................................................. 15
Kräfte ............................................................................................................................... 15
Kraft und Masse ................................................................................................................ 16
Die NEWTONschen Axiome............................................................................................... 17
Impulserhaltung................................................................................................................. 18
Einfache Bewegungen....................................................................................................... 19
Reibungskräfte .................................................................................................................. 21
4.
Arbeit und Energie.......................................................................................................... 23
4.1.
4.2.
4.3.
4.4.
Mechanische Energie ........................................................................................................ 23
Potentielle Energie ............................................................................................................ 25
Feldkraft und potentielle Energie...................................................................................... 26
Der Energiesatz der Mechanik .......................................................................................... 27
5.
Gravitation....................................................................................................................... 28
5.1.
5.2.
5.3.
Drehimpuls und Drehmoment........................................................................................... 28
Das Gravitationsgesetz...................................................................................................... 30
Potentielle Energie und Gravitationspotential .................................................................. 32
II
Inhaltsverzeichnis
5.4.
Planetenbewegung............................................................................................................. 32
6.
Schwingungen I ............................................................................................................... 34
6.1.
6.2.
6.3.
Der Federschwinger .......................................................................................................... 34
Das Pendel......................................................................................................................... 37
Gedämpfte Schwingungen ................................................................................................ 38
7.
Systeme von Massenpunkten; Stöße ............................................................................. 41
7.1.
7.2.
7.3.
7.4.
7.5.
7.6.
Der Schwerpunkt............................................................................................................... 41
Stöße: Grundlagen............................................................................................................. 42
Elastische Stöße im Laborsystem...................................................................................... 43
Stöße im Schwerpunktsystem ........................................................................................... 45
Inelastische Stöße.............................................................................................................. 45
Nichtzentrale Stöße ........................................................................................................... 46
8.
Bewegte Bezugssysteme .................................................................................................. 47
8.1.
8.2.
8.3.
8.4.
Vorbemerkungen............................................................................................................... 47
Bezugssysteme mit konstanter Relativgeschwindigkeit u << c........................................... 47
Linear beschleunigte Bezugssysteme................................................................................ 48
Rotierende Bezugssysteme................................................................................................ 49
9.
Der starre Körper; Rotation I........................................................................................ 52
9.1.
9.2.
9.3.
9.4.
9.5.
Einleitung .......................................................................................................................... 52
Kräfte und Drehmoment an starren Körpern .................................................................... 53
Trägheitsmoment............................................................................................................... 53
Dynamik bei der Rotation ................................................................................................. 55
Zusammenstellung wichtiger formaler Analogien............................................................ 58
10.
Rotation II........................................................................................................................ 59
10.1. Trägheitstensor.................................................................................................................. 59
10.2. Trägheitsellipsoid.............................................................................................................. 60
10.3. Symmetrischer Kreisel ...................................................................................................... 62
11.
Deformierbare Festkörper ............................................................................................. 65
11.1.
11.2.
11.3.
11.4.
Dehnung und Kompression............................................................................................... 65
Scherung............................................................................................................................ 67
Der gebogene Balken ........................................................................................................ 69
Inelastisches Verhalten...................................................................................................... 71
12.
Flüssigkeiten .................................................................................................................... 73
12.1.
12.2.
12.3.
12.4.
12.5.
12.6.
Einleitung .......................................................................................................................... 73
Statischer Druck ................................................................................................................ 73
Schweredruck.................................................................................................................... 75
Auftrieb und Schwimmen ................................................................................................. 76
Oberflächenspannung........................................................................................................ 77
Fest-flüssig-Grenzflächen ................................................................................................. 79
III
Inhaltsverzeichnis
13.
Gase .................................................................................................................................. 82
13.1. Kompressibilität ................................................................................................................ 82
13.2. Schweredruck in Gasen..................................................................................................... 83
14.
Strömende Flüssigkeiten und Gase ............................................................................... 85
14.1.
14.2.
14.3.
14.4.
14.5.
14.6.
Vorbemerkungen............................................................................................................... 85
Innere Reibung .................................................................................................................. 86
Beispiele für laminare Strömungen................................................................................... 87
Turbulente Strömungen, Ähnlichkeit, Strömungsgrenzschicht ............................................ 89
Reibungsfreies Fluid: BERNOULLIsche Gleichung............................................................ 92
Strömungswiderstand........................................................................................................ 95
15.
Schwingungen II.............................................................................................................. 97
15.1.
15.2.
15.3.
15.4.
15.5.
2D-Überlagerung von Schwingungen............................................................................... 97
Schwebungen .................................................................................................................... 97
Die FOURIER-Analyse........................................................................................................ 98
Gekoppelte Schwinger .................................................................................................... 100
Erzwungene Schwingungen ............................................................................................ 101
16.
Wellen............................................................................................................................. 104
16.1.
16.2.
16.3.
16.4.
16.5.
Einleitung ........................................................................................................................ 104
Wellengleichungen.......................................................................................................... 106
Arten von Wellen ............................................................................................................ 106
Wellenausbreitung in verschiedenen Medien ................................................................. 107
Überlagerung von Wellen; Gruppengeschwindigkeit..................................................... 110
17.
Wellenausbreitung ........................................................................................................ 113
17.1.
17.2.
17.3.
17.4.
17.5.
17.6.
17.7.
Streuung .......................................................................................................................... 113
Das HUYGENSsche Prinzip .............................................................................................. 113
Das FERMATsche Prinzip................................................................................................. 114
Beugung .......................................................................................................................... 115
DOPPLER-Effekt; MACHsche Wellen............................................................................... 116
Intensität einer Welle ...................................................................................................... 118
Reflexion und Transmission an einer Grenzfläche ......................................................... 119
18.
Akustik ........................................................................................................................... 121
18.1. Einleitung ........................................................................................................................ 121
18.2. Töne und Klänge ............................................................................................................. 121
18.3. Stehende Wellen; Musikinstrumente .............................................................................. 123
LITERATURLISTE...................................................................................................... V
QUELLENVERZEICHNIS ...........................................................................................VI
SACHREGISTER ...................................................................................................... VII
IV
Einleitung
A. EINLEITUNG
Einleitung
1.
Einleitung
1.1.
Was ist Physik
−
−
−
−
ϕυσιζ = Ursprung, Naturordnung, das Geschaffene lt. den griechischen Naturphilosophen, z.B. Aristoteles (384 - 322 v.d.Z.)
im Gegensatz zur Metaphysik (das, was im Aristoteleschen System nach der
Physik behandelt wird, also die gesamte ideelle Welt)
griechische Naturphilosophie:
·
Beginn des naturwissenschaftlichen Denkens; Entmythologisierung der Natur
·
Natur als (sehr komplizierter) Mechanismus, den man im Prinzip verstehen kann;
Gesetzmäßigkeiten statt undurchschaubares Wirken von Göttern und Dämonen
weitere Etappen:
·
klassische Physik
~ 1920
·
moderne Physik (Quantenphysik, Relativität)
−
„Verständnis der Natur“ = Erkennen von Gesetzmäßigkeiten
−
→ Naturbeobachtung ⇒ Schlussfolgerung (z.B. Gesetze der Planetenbewegung)
−
Bloßes Beobachten reicht oft nicht aus, da die Natur zu kompliziert ist (Überlagerung von Einflüssen), und man z.B. auch optischen Täuschungen zum Opfer
fallen kann
⇒
−
1.2.
−
(gezieltes) Experiment = „Frage an die Natur“
= Ausschluss störender Einflüsse, ggf. Verstärkung
des gewünschten/interessierenden Effektes
Mit dem Experiment eng verknüpft sind zwei weitere Komplexe:
·
physikalische Größen, Maßeinheiten, Messung, Messfehler (vgl. <1.2.>)
·
physikalische Modelle, Theorien, Rolle der Mathematik (vgl. <1.3.>)
Die Rolle des Experimentes
Wesen des Experimentes ist die Messung (= Vergleich zweier Größen)
Beispiel:
n
Physikalische Größe Länge hat Maßeinheit Meter (m). Vergleich einer gegebenen Distanz mit dieser Maßeinheit ⇒ „Distanz beträgt 1,54 m“
−
Maßeinheiten sind durch Normale oder Standards definiert; Messgeräte müssen
regelmäßig mit diesen verglichen (geeicht, kalibriert) werden
−
Die verwendeten Normale hängen vom Entwicklungsstand von Wissenschaft
und Technik ab.
2
Einleitung
n
Beispiel: Meter
–
−
1799:
1/10.000.000 des Erdquadranten
1875:
Urmeter (Pt-Ir-Stab mit Strichen)
∆x = 10 −3 mm
∆x
= 10 −6
x
1960:
über die Wellenlänge einer bestimmten
Strahlung, die Krypton-86-Atome aussenden
∆x
= 10 −8
x
1983:
(wegen der inzwischen erreichten enormen
Genauigkeit der Zeitmessung)
∆t
≈ 10 −14
t
Grundgrößen
â
Länge s
Zeit t
„1 m ist die Strecke, die das Licht im Vakuum
1
in
zurücklegt“.
299792458 s
!
Damit ist c keine Messgröße mehr und beträgt
definitionsgemäß 299.792.458 mžs-1!
!
und
}
abgeleitete Größen, z.B.
â
s
Geschwindigkeit v =
t
Über die Auswahl der Grundgrößen sind bestimmte Maßsysteme definiert. Seit
1960 in vielen Ländern verbindlich: SI-System (le Système International d‘ Unitès)
7 Grundgrößen
Länge
Zeit
Masse
elektrische Stromstärke
Temperatur
Stoffmenge
Lichtstärke
mit der entsprechenden SI-Basiseinheit
Meter
m
Sekunde
s
Kilogramm
kg
Ampere
A
Kelvin
K
Mol
mol
Candela
cd
Kommentar:
Alle anderen Größen sind aus den Grundgrößen abgeleitet, ebenso ihre
Maßeinheiten aus den Basiseinheiten. Allerdings haben manche abgeleiteten
Einheiten eigene Namen (N, J, W, V, ...)
·
Die Auswahl der Grundgrößen erfolgt nach Zweckmäßigkeit. Prinzipiell
würden drei Grundgrößen, z.B. Länge, Zeit, Masse reichen!
SI
u
·
3
Einleitung
·
–
Es gibt immer noch/immer wieder:
∗ SI-fremde Maßeinheiten, z.B. Torr, atm, cal, yard, inch, ...
∗ andere Maßsysteme
â
ggf. anderes Aussehen von Formeln;
z.B. tritt beim CGS-System (cm-g-sec) das 1/4πε0 in den Gleichungen
der Elektrodynamik
und
Messgenauigkeit
â
wie groß ist der maximal mögliche Fehler?
-reproduzierbarkeit
â
liefert Wiederholung der Messung zu anderer
Zeit und/oder anderen Bedingungen dasselbe
Ergebnis?
⇒ Dies nicht so wichtig für die Schauversuche der Vorlesung, jedoch sehr für
wissenschaftliche Arbeit.
⇒ siehe Praktikum!
1.3.
−
Physikalische Modelle und Theorien
Experimente meist so gestaltet, dass bestimmte Einflüsse deutlich messbar sind,
andere (störende) Einflüsse dagegen unterdrückt werden.
n
Beispiel:
Fallgesetz:
–
–
–
Körper mit hoher Massendichte
kein Wind u.a.
am besten Vakuumturm
⇒ Fall-Verhalten nur von Masse des Körpers abhängig, alle sonstigen Eigenschaften
(Dichte, Form, ....) sind unerheblich
⇒ Bild (Modell) der Punktmasse
−
Physikalische Gesetze, die in der Regel durch Formeln ausgedrückt werden,
sind den Vereinfachungen des Modells angepasst, d.h., Dinge, die in dem betrachteten Zusammenhang keine Rolle spielen, kommen nicht mehr vor.
⇒
−
Einfachheit und Klarheit. Man muss aber immer wieder überprüfen, ob die
Voraussetzungen des Modells im konkreten Fall gelten
Hypothesen
·
sind mehr oder weniger („Arbeitshypothese“) begründete Vermutungen
·
dienen oft dem Entwurf von Experimenten („Wenn ... so ist, dann müsste doch ...“)
·
sind die Vorstufen von Gesetzmäßigkeiten
Prinzipiell ist die Physik natürlich immer offen für unerwartete experimentelle
Ergebnisse, insofern ist keine Gesetzmäßigkeit „absolut“. Mit zunehmender
Vervollständigung des Bildes von der Welt, der zunehmenden Menge von zusammenpassenden und sich gegenseitig stützenden Befunden, steigt natürlich
4
Einleitung
das Zutrauen in die gefundenen Gesetzmäßigkeiten. Deshalb wird z.B. die Suche
nach einem perpetuum mobile als Zeitverschwendung abgelehnt.
−
Theorien sind die (überwiegend mathematische) Formulierung gefundener oder hypothetischer1 Gesetzmäßigkeiten. Sie beziehen sich auf ein bestimmtes physikalisches
Modell, d.h., bestimmte Bedingungen (z.B. das Fehlen von Reibung beim Fallgesetz).
·
wichtige Rolle der Mathematik und der Computertechnik
·
Arbeitsteilung Experimentalphysik - Theoretische Physik wegen des enormen Wissensvolumens (Kepler, Newton, Galilei waren nicht spezialisiert!)
·
„Experimente mit dem Computer“ = Herausfinden der wesentlichen Gesetzmäßigkeiten/Theoriebildung anhand experimentell überprüfter Konstellationen
und Berechnung experimentell praktisch unzugänglicher Konstellationen
1.4.
Der „Stammbaum der Physik“
Bedeutung der Mechanik:
grundlegend für vieles andere
·
beispielhaft (z.B. bezüglich
Modellbildung)
·
({1}, S. 14)
1.5.
Wichtige Größen und Maßeinheiten
1.5.1.
Länge: m
103
10-3
10-6
10-9
10-12
10-15
1
m
m
m
m
m
m
1 km
1 mm
1 µm
1 nm
1 pm
1 fm
Vorsilbe lt. SI-System
kilo
milli
mikro
→
nano
pico
femto
→
}
feinstbearbeitete Oberfläche
Atomkern-Durchmesser
Es gibt auch Theorien, die zunächst hypothetisch sind!
5
Einleitung
10-10 m
1Å
Angström
1 Lichtjahr
1 Parsec
1 Lj
1 pc
= 9,465 ž 1015 m
= 3 ž 1016 m
1.5.2.
→
Atom-Durchmesser
Zeit: s
Die Sekunde ist definiert als das 9.192.631.770-fache der Periodendauer eines bestimmten Übergangs zwischen Energieniveaus des 133Cs-Atoms.
5 ž 1017 s
1 ž 1017 s
Alter des Universums
Alter der Erde
2 ž 1013 s
Zeit seit der Entwicklung des ersten Menschen
10-3
10-6
10-9
10-12
10-15
1 ms
1 µs
1 ns
1 ps
1 fs
1.5.3.
s
s
s
s
s
→
→
→
Anregungsdauer eines Atoms
ultrakurzer Laserpuls; „Ultrakurzzeitphysik“
Periodendauer einer Lichtwelle
Masse: kg
Masse (zur Zeit noch) definiert über den in Paris aufbewahrten 1 kg-Pt-Ir-Zylinder
(früher: 1 dm3 H2O bei 4 °C).
Angestrebt:
!
Übergang zu Si-Einkristallkugel mit definierter Atomanzahl (= Anschluss an genauer messbare atomare Einheiten)
extreme Beispiele:
1.5.4.
!
Masse eines Elektrons:
Masse der Sonne:
Masse der Milchstraße:
10-30 kg
1030 kg
1042 kg
Temperatur: K
Ein Kelvin ist der 273,16te Teil der thermodynamischen Temperatur am Tripelpunkt
des Wassers. (Der Tripelpunkt des Wassers liegt bei 273,16 K = 0,01 °C.)
!
6
Einleitung
1.5.5.
Winkel
Im Alltag, in der
Geographie usw.:
1° =
zweckmäßig:
Bogenmaß =
1
Vollkreis
360
1° = 60‘
= 60 ž 60“
(Bogenminute) (Bogensekunde)
Dann ist der Vollkreis =
!
Bogenlänge L
Radius R
!
2πR
= 2π .
R
Streng genommen hat der Winkel im Bogenmaß auch eine Maßeinheit:
SI-Einheit: der Radiant; [α] = rad = m ž m-1
SI
Der Vollkreis ist also 2π rad ≈ 6,28 rad; 1 rad ≈ 57°
Der Physiker spricht aber von „Winkel 3/4π“ o.ä.
1.5.6.
Raumwinkel
Der Raumwinkel ist definiert über die eingeschlossene Fläche S auf der Kugeloberfläche, geteilt durch das Quadrat des Kugelradius.
Ω=
Der Vollwinkel ist daher Ω =
!
S
R2
4πR 2
= 4π .
R2
Kommentar:
− Die Fläche S ist ein beliebiger (in sich geschlossener) Teil der Kugeloberfläche.
− Der Raumwinkels u.a. wichtig für die Beschreibung von Strahlungsemission.
− SI-Einheit: der Steradiant; [Ω] = sr = m2 ž m-2
u
SI
7
Mechanik
B. MECHANIK
Mechanik - Kinematik
2.
Kinematik
... ist die Lehre von der Bewegung. Sie beschreibt Bewegungen, ohne nach den Ursachen zu fragen.
2.1.
−
!
Ortsvektor
Der Ort eines Massepunktes P zum Zeitpunkt t wird beschrieben durch den
r
Ortsvektor r ( t ) mit dem Ursprung 0:
!
Der Ursprung wird entsprechend dem physikalischen Problem zweckmäßig gewählt, z.B.: Abwurfstelle beim Wurf, Rotations-Mittelpunkt bei Rotation.
−
r r
Wenn sich P relativ zu 0 bewegt, ist r = r ( t ) . Die Gesamtheit der Endpunkte
r
von r heißt Bahnkurve:
−
r
Je nach dem physikalischen Problem wird man r in unterschiedlicher Weise in
Komponenten zerlegen:
·
im allgemeinen Fall entsprechend den kartesischen Koordinaten:
r
r
r
r
r = x⋅ i + y⋅ j + z⋅k
r r r
i , j, k ... Einheitsvektoren in x-, y-, und z- Richtung,
·
2.2.
−
!
(1)
bei einer Rotationsbewegung wird man oft Polarkoordinaten wählen (vgl. <2.4.>).
Geschwindigkeit
... ist die Änderung des Ortsvektors mit der Zeit:
!
9
Mechanik - Kinematik
r
r
r
r (t 2 ) − r (t1 ) ∆r
r
v(t 1 , t 2 ) =
=
t 2 − t1
∆t
−
r
v ist die mittlere Geschwindigkeit im Intervall (t1, t2). Beliebige Eskapaden innerhalb dieses Intervalls (siehe Abbildung) bleiben unbemerkt/unberücksichtigt!
⇒
Die Momentangeschwindigkeit zu einem bestimmten Zeitpunkt erhält
man durch Grenzübergang t2 → t1:
r
r
r
r (t 2 ) − r (t 1 ) dr
r
r
=
v( t 1 ) = lim
( t 1 ) = r& ( t 1 )
t 2 → t1
t 2 − t1
dt
2.3.
−
... ist die Änderung der Geschwindigkeit mit der Zeit
(„v ist Tangente an die Bahnkurve“):
!
r
Man sieht, dass sich v im Allgemeinen sowohl im Betrag als auch in der Richtung ändert! Die Beschleunigung ist ein Vektor.
!
m
s2
(4)
Analog zu Gl. (3) erhalten wir die (momentane) Beschleunigung zum Zeitpunkt t1:
r
r
r
r
r
v ( t 2 ) − v ( t 1 ) dv
r
d2r
a ( t 1 ) = lim
=
( t 1 ) = 2 ( t 1 ) = &r&( t 1 )
t 2 → t1
t 2 − t1
dt
dt
−
SI
mittlere Beschleunigung im Intervall (t1, t2):
r
r
r
r
v( t 2 ) − v( t 1 ) ∆v
a (t1 , t 2 ) =
=
t 2 − t1
∆t
−
(3)
Beschleunigung
Maßeinheit: [a] =
−
(2)
(5)
2 Grenzfälle der Beschleunigung (bzw. Komponenten im allgemeinen Fall):
a) Tangentialbeschleunigung (tangential zur Bahnkurve)
r
r
r
r r
a ~ ∆v wirkt parallel (oder antiparallel) zu v ( ∆v || v )
r
⇒ es ändert sich nur v , nicht die Richtung
10
Mechanik - Kinematik
b) Normalbeschleunigung (normal zur Bahnkurve)
r
r
r
r r
a ~ ∆v wirkt senkrecht zu v ( ∆v⊥v )
r
⇒ es ändert sich nur die Richtung, nicht v
n
Beispiel:
Auf der Erde unterliegt jeder nicht fixierte Körper einer Beschleunigung.
a ≈ 9,81 m · s-2 ≡ g ... Erdbeschleunigung
⇒
v nimmt zeitlinear zu:
dv
dt
m
s2
t
m
v( t ) = ∫ 9,81 2 dt ′
s
0
⇒
= 9,81
v( t ) = 9,81
m
⋅t
s2
Fallstrecke s:
ds( t )
dt
= v( t )
t
s( t ) = ∫ v( t ′) ⋅ dt ′ = 9,81
0
⇒
t
1s
2s
3s
2.4.
−
s( t ) =
t
m
∫ t ′ ⋅ dt ′
s2 0
9,81 m 2
⋅t
2 s2
v(t)
9,8 m·s-1
19,6 m·s-1
28,4 m·s-1
s(t)
4,9 m
19,6 m
44,1 m
(= 1 · 4,9)
(= 4 · 4,9)
(= 9 · 4,9)
Beschreibung der Kreisbewegung
Bei der Kreisbewegung ist der Abstand r konstant.
⇒ Einführung von Polarkoordinaten zweckmäßig
11
Mechanik - Kinematik
r2 = x 2 + y2
y
y
=
= sin ϕ
r
x 2 + y2





Transformationsgleichungen
{x, y} ↔ {r, ϕ}
⇒ Verallgemeinerung: Zylinderkoordinaten (für rotationssymmetrische Probleme)
{x, y, z} ↔ {r, ϕ, z}
r
Nun zur Kreisbewegung (hier ist r = r = const. !):
−
Winkelgeschwindigkeit ω
ω=
−
(6)
Winkelbeschleunigung α
α=
−
dϕ( t )
= ϕ& ( t )
dt
dω( t ) d 2 ϕ( t )
&&( t )
=
=ϕ
dt
dt 2
Zusammenhang mit Umlaufgeschwindigkeit, -beschleunigung:
s = r⋅ϕ
s& = v = r ⋅ ϕ& = r ⋅ ω
&s& = a = v& = r ⋅ ω
& = r⋅α
−
(7)





(8)
Bis hierher: Rotation in der Ebene. Im 3D betrachtet man ω und α zweckmäßigerweise als Vektoren.
Richtung
Beträge:
r
ω =ω
r
α =α
→
durch Rotationsebene festgelegt
lt. Gl. (6)
lt. Gl. (7)
12
Mechanik - Kinematik
Rechte-Hand-Regel!
−
r
α kann bei gegebener Rotationsrichtung nach oben oder unten zeigen:
r
r
α1 ~ ω
r
r
α 2 ~ −ω
−
→
→
Vektorschreibweise von Gl. (8) (dann stimmen Betrag und Richtung):
r r r
v = ω× r
r r r
a = α× r
2.5.
−
Beschleunigung
Abbremsung



(9)
Überlagerung von Bewegungen
Die Zusammenhänge zwischen Ort, Geschwindigkeit und Beschleunigung gelten für jede Komponente einzeln. Dies erleichtert vieles!
!
z.B. in kartesischen Koordinaten:
r
r
r
r
r
= x⋅ i + y⋅ j + z⋅k
r
r
v = &r
r
r
r
= x& ⋅ i + y& ⋅ j + z& ⋅ k
r
r
r
= vx i + vy j + vzk
r
r
a = v&
r
r
r
r
= &r& = &x& ⋅ i + &y& ⋅ j + &z& ⋅ k
r
r
r
= a x i + a y j + a zk
(1)







(10)
n
Beispiel:
Waagerechter Wurf
r
r
v0 = vx ⋅ i
Waagerecht findet eine gleichförmige Bewegung statt (vx = const.) und senkrecht eine
gleichmäßig beschleunigte Bewegung (freier Fall, d.h. a = g = const.), die sich überlagern.
13
Mechanik - Kinematik
Man kann natürlich auch für jeden Zeitpunkt Betrag und Richtung der resultierenden
Geschwindigkeit ermitteln:
r
v( t )
= v 2x ( t ) + v 2y ( t ) = v 2x + g 2 t 2
tan β =
vx
vy
14
Mechanik – Dynamik
3.
Dynamik
Jetzt fragen wir nach der Ursache der Änderung des Bewegungszustandes, also nach
der Ursache der Beschleunigung.
3.1.
!
Trägheit
Änderung des Bewegungszustandes heißt Änderung der Geschwindigkeit.
!
Schon Galilei (1564 - 1642) hat erkannt, dass eine geradlinig gleichförmige Bewer
gung, d.h. v = const. , von sich aus fortbesteht, also keiner besonderen Ursache bedarf. Ruhe ist ein Sonderfall davon.
Man bezeichnet dies als Trägheitsprinzip.
3.2.
−
Kräfte
Eine Änderung des Bewegungszustandes eines Körpers setzt eine Wechselwirkung voraus → Konzept der Kräfte
Änderung des Bewegungszustandes
}
↔
{
!
„am Körper greift
eine Kraft an“
Kräfte können die verschiedenartigsten Ursachen haben.
−
Eigenschaften von Kräften
·
Kräfte sind Vektoren, also bestimmt durch Betrag und Richtung
·
Bei mehreren Kräften überlagern sich alle Komponenten einzeln,
z.B. für kartesische Koordinaten:
r
r
Fges = ∑ Fi
i
r
r
Fx ,ges = ∑ Fx ,i
i
r
r
Fy,ges = ∑ Fy,i
i
r
r
Fz ,ges = ∑ Fz ,i
i
!









(1)
Auch hier gelten natürlich wieder (vgl. Gl. (2 - 10)) die
Zusammenhänge für jeder Koordinate einzeln!
−
r
Ein Körper oder Massepunkt mit Fges = 0 heißt „frei“, d.h., er ändert seinen Bewegungszustand nicht .
15
Mechanik – Dynamik
−
In vielen Fällen hängt die Kraft vom Ort ab, d.h.
r r r
F = F( r ) ,
also Betrag und Richtung der Kraft sind eindeutig dem Ort zugeordnet.
Eine solche jedem Raumpunkt zugeordnete Kraft wird als Kraftfeld bezeichnet.
n
Beispiel:
Gravitation/Erde
Also:
r
Jeder Punkt r in der Umgebung der Erde besitzt die Eigenschaft, auf eine ber r
stimmte Masse eine ganz bestimmte Kraft F( r ) auszuüben.
Diese Eigenschaft hat der Punkt auch dann, wenn keine zweite Masse dort ist.
3.3.
−
Kraft und Masse
Unterschiedliche Körper reagieren auf ein und dieselbe Kraft unterschiedlich.
z.B.:
−
⋅ Ziehen am Handwagen ⇔ an einem PKW
⋅ Abbremsen eines großen Schiffes
Die Eigenschaft, sich der Einwirkung der Kraft zu widersetzen und den alten
Bewegungszustand möglichst beizubehalten (Trägheit) wird durch die träge
Masse beschrieben. Es gilt:
r
r
r
r
F = m ⋅ a ( = mv& = m&r& )
!
!
(2)
Dies ist das NEWTONsche Aktionsprinzip.
− Es kann in dreierlei Weise interpretiert werden:
a)
u
r
r
r
F = m ⋅ a (Gl. (2)): Bestimmung von F ;
r
„Wenn ein Körper der Masse m eine Beschleunigung a
erfährt, wie groß ist dann die wirkende Kraft?“
(z.B.: Ermittlung der Erdschwerkraft aus Fallexperiment)
16
Mechanik – Dynamik
b)
c)
−
r
F
m = r :
a
Charakterisierung der Trägheit;
„Wie viel Kraft muss pro Beschleunigung aufgewandt
werden?“
r
&rr& = ar = 1 ⋅ F :
m
r
Bestimmungsgleichung für a . Damit kann letztlich bei
r
gegebener Kraft F( t ) für eine bestimmte Masse m die
r
Bahnkurve r ( t ) durch Integration bestimmt werden.
Lesart a) bzw. Gl. (2) führen zur Definition der Maßeinheit für die Kraft aus den
SI-Grundgrößen Masse, Länge und Zeit:
1 Newton = 1 N = 1 kg ⋅
−
m
s2
SI, (3)
r
m
Also: 1 N ist die Kraft, die einer Masse von 1 kg die Beschleunigung a = 1 2 verleiht.
s
m
Die Beschleunigung durch die Erdschwerkraft auf der Erdoberfläche beträgt g ≈ 9,81 2 .
s
⇒ 1 kg besitzt auf der Erdoberfläche die Gewichtskraft
r
m
FG = 9,81 kg ⋅ 2 = 9,81 N = 1 kp
s
Die Gewichtskraft darf nicht mit der Masse verwechselt werden.
Die Maßeinheit Kilopond ist über g definiert. Daher besser N verwenden!
3.4.
Die NEWTONschen Axiome
Die Grundgesetzmäßigkeiten der Bewegung von Körpern unter dem Einfluss von
Kräften hat Newton (1643 - 1727) in folgenden Axiomen formuliert:
1.
2.
(Trägheitsprinzip): Jeder Körper verharrt in Ruhe oder der gleichförmigen geradlinigen Bewegung, solange keine Kraft auf ihn einwirkt.
!
r
(Aktionsprinzip): Wenn eine Kraft F auf einen Körper mit der Masse m wirkt,
beschleunigt sie ihn mit:
!
r
r &r& F
a=r=
m
3.
(Reaktionsprinzip): Bei zwei Körpern, die nur miteinander wechselwirken ist
r
r
die Kraft F1 auf Körper A entgegengesetzt der Kraft F2 auf Körper B:
r
r
F1 = − F2
(4)
!
(5)
„Actio = Reactio“
17
Mechanik – Dynamik
Newton hatte 2. anders formuliert, und zwar unter Zuhilfenahme des Impulses:
r
r
p = m⋅v
(6)
r
Der Impuls ist ein Vektor ~ v .
Maßeinheit: [p] = kg ⋅
!
m
s
SI
r
Newton schrieb: Eine Kraft F ändert bei ihrer Einwirkung auf einen Körper dessen Impuls entsprechend.
r dpr d(m ⋅ vr )
F=
=
dt
dt
(7)
Anwendung der bekannten Differentiations-Regeln liefert:
r
r
r dm
dv
F = m⋅
+ v⋅
dt
dt
r
r
F = m⋅a
+0
⇒
Nur für konstantes m folgt Gl. (4)!
Als ob Newton die Relativitätstheorie geahnt hätte!
3.5.
−
Impulserhaltung
Das 2. NEWTONsche Axiom besagt:
⇒ Ein Teilchen, auf das keine Kraft wirkt, ändert seinen Impuls nicht.
Gegeben ist nun: System aus vielen Teilchen, keine Kraft von außen:
⇒ keine von außen aufgeprägten Impulsänderungen
−
Welche Rolle spielen innere Wechselwirkungen (zwischen den Teilchen)?
Betrachtung am Beispiel zweier Teilchen:
Teilchen 1 verursacht F1 auf Teilchen 2:
⇒
∆p 2 = F1 ⋅ ∆t
aber: Teilchen 2 verursacht ebenfalls eine Kraft, F2, auf Teilchen 1:
⇒
∆p1 = F2 ⋅ ∆t
Wegen des 3. NEWTONschen Axioms ist:
⇒
F1 = −F2
∆p1 = −∆p 2 , also
∆p1 + ∆p 2 = ∆p ges = 0
18
Mechanik – Dynamik
−
Fazit/Verallgemeinerung auf viele Teilchen:
In einem abgeschlossenem System, d.h. einem System ohne Wechselwirkung
mit äußeren Kräften, ist der Gesamtimpuls konstant:
r
r
p ges = ∑ p i = const.
!
(8)
i
Die Bedingung „abgeschlossenes System“ lässt Reibung ohne weiteres zu!
3.6.
Einfache Bewegungen
3.6.1.
−
Die gleichmäßig beschleunigte Bewegung
r
In der Nähe der Erdoberfläche ist g einigermaßen konstant ⇒ alle Wurfbewegungen sind gleichmäßig beschleunigt (Luftreibung vernachlässigt):
r r
a = g = const.
!
(Erdbeschleunigung)
n
Beispiel:
senkrechter Wurf nach oben mit:
r
r
r
↑ v ( 0) ≡ v 0 , ↓ g
→ skalare Schreibweise1:
−g =
dv
dt
t
⇒
v( t ) = ∫ − g ⋅ dt '
0
v( t ) = v 0 − gt
t
⇒
x ( t ) = ∫ v( t ' ) ⋅ dt '
0
x(t) = x 0 + v 0 t −
1
g 2
t
2
r
m
Unter g verstehen wir jetzt g = 9,81 2 . Das negative Vorzeichen entspricht der Tatsache,
s
dass g in die negative Koordinatenrichtung zeigt.
19
Mechanik – Dynamik
−
Wie hier nicht bewiesen werden soll, gelten für beliebige Richtungsbeziehungen
r
r
zwischen a = const. und v 0 = const. die analogen Vektorbeziehungen:
r
r
r
v( t ) = v 0 + a ⋅ t
r
r
r r
a 2
r ( t ) = r0 + v 0 ⋅ t + t
2
und
3.6.2.
−
(9)
(10)
Die gleichförmige Kreisbewegung
Wir hatten in <2.4.> die Winkelgeschwindigkeit eingeführt:
ω = ϕ&
−
Die Umlaufzeit T für eine Umdrehung, d.h. für ∆ϕ = 2π, ergibt sich wie folgt:
ω=
−
(2 - 6)
dϕ 2 π
=
dt
T
⇒
T=
2π
ω
(11)
Damit folgt für die Umdrehungsfrequenz ν (in 1/Zeiteinheit):
ν=
1
ω
=
T 2π
(12)
also ist
ω = 2π ⋅ ν
Die Winkelgeschwindigkeit (sogenannte „Kreisfrequenz“ ) ist also das 2π-fache
der Umdrehungsfrequenz (weil pro Umdrehung ein Winkel von 2π überstrichen
wird).
−
(13)
!
Welche Beschleunigung erfährt eine rotierende Masse?
Wir betrachten die Beträge:
r
r
r
r
r
r = r , v = v , a = a , ∆ r = ∆r , ∆v = ∆v
20
Mechanik – Dynamik
a=
dv
dt
(14)
Wegen der Ähnlichkeit der Dreiecke ist:
∆r ∆v
=
r
v
⇒
∆v =
v
⋅ ∆r
r
Dies in (14) eingesetzt ergibt:
⇒
a =
v ∆r
⋅
r ∆t
a = ω⋅ r ⋅ ω
∆r
dϕ
= r⋅
= r⋅ω
∆t
dt
v
=ω
r
(2 - 8)
a = ω2 ⋅ r
−
(15)
Um eine Masse m auf einer Kreisbahn zu halten, braucht man die Kraft:
F = m ⋅ a , d.h. mit Gl. (15)
r
r
F = −mω 2 r
(16)
Dies ist die Zentripetalkraft, die z.B. durch ein Seil aufgebracht werden muss,
um einen Körper auf einer Kreisbahn zu halten. (vgl. <8.4.>)
3.7.
Reibungskräfte
3.7.1.
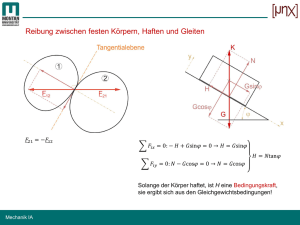
Reibung zwischen festen Körpern
!
Reibung hat negative und positive Seiten, wie jeder bei Glatteis merkt!
a) Gleitreibung:
empirisch findet man:
FR = µ ⋅ FN
µ ... Reibkoeffizient
Kommentar:
− µ gilt für bestimmte Materialpaarung
− Deutung: mikroskopische Oberflächen-Rauheit
− unabhängig von Auflagefläche/-druck
− unabhängig von Geschwindigkeit
(17)
u
} Näherung!
21
Mechanik – Dynamik
b) Haftreibung:
FH = µ H ⋅ FN ( µ H > µ )
µ H ... Haftreibungskoeffizient
(18)
Deutung: „Herausheben aus Anfangs-Verhakung“
Kommentar zur Reibung zwischen Festkörpern:
−
−
−
−
u
Reduzierung der Reibung durch Schmierung
Vermeiden der Reibung (Kugellager)
in der Realität beliebig kompliziert:
·
Luftsauerstoff ⇒ chemische Reaktionen,
·
Schmiermittel,
·
Oberflächengestalt.
Bezug zur Kontaktmechanik
3.7.2.
Reibung in Flüssigkeiten oder Gasen
−
Ein Körper, der sich durch ein zähes Medium bewegt, wird ebenfalls gebremst.
(vgl. <14.>)
−
Hier soll zunächst nur die Formel gegeben werden. Für eine Kugel gilt:
(Der Faktor 6πr ist spezifisch für die Kugel)
â
FR = −6πr ⋅ η ⋅ v
η ... Viskosität (Zähigkeit)
v ... Geschwindigkeit
Wichtig: FR ~ v
!
(19)
⇒ Sättigung der Geschwindigkeit bei konstanter Kraft
(z.B. freier Fall).
22
Mechanik – Arbeit und Energie
4.
Arbeit und Energie
4.1.
Mechanische Energie
−
Goldene Regel der Mechanik:
Was man an Kraft gewinnt, muss man an Weg zusetzen (und umgekehrt).
!
Offensichtlich ändert es das Ergebnis nicht, wenn sich Kraft und Weg ändern,
solange nur das Produkt aus Kraft und Weg konstant ist.
−
Definition: mechanische Arbeit
r r
∆W = F ⋅ ∆ r
−
(1)
Arbeit ist ein Skalar
!
entscheidend ist die Kraftkomponente in Wegrichtung:
r r r
r
F ⋅ ∆ r = F ⋅ ∆ r ⋅ cos γ
r
= Ft ⋅ ∆ r
Ft ... Tangentialkomponente
Kräfte ⊥ Wegelement (Fn) leisten keine Arbeit (sogenannte Zwangskräfte)
−
Für einen makroskopischen Weg erhält man statt (1) verallgemeinert:
W=
r
F
∫ ⋅ dr
(2)
Weg
−
Maßeinheit für die Arbeit ist das Joule: [W] = J
1 J = 1 Nm = 1 kg ž
m
s2
SI
žm
23
Mechanik – Arbeit und Energie
−
n
Beispiel: Beschleunigungsarbeit
r
F
r
dv
= m⋅
(2. NEWTONsches Axiom)
dt
Die Kraft ist der Trägheitskraft entgegengerichtet, die ihrerseits der Beschleunigung entgegengerichtet ist.
W
r r
= ∫ F ⋅ dr
r r
d r = v ⋅ dt
r
v2
W
r
dv r
= ∫ m ⋅ v dt
r
dt
v
W
mr
mr
= v 22 − v12 = ∆E kin
2
2
1
mit
m r2
v
2
Ekin ... kinetische Energie, Bewegungsenergie
E kin ≡
(3)
Die beim Beschleunigen des Teilchens aufgewandte Arbeit steckt als Änderung
der kinetischen Energie in der bewegten Punktmasse.
−
Beispiel: Hubarbeit
r
F
n
r
= −m ⋅ g
(Minuszeichen, weil die aufzuwendende Kraft der Erdschwerkraft entgegengerichtet ist!)
r
r2
W
r
= ∫ − m ⋅ g ⋅ dr
r
r1
h
skalar:
W
= ∫ m ⋅ g ⋅ dr
0
r
(Bei skalarer Schreibweise fällt das Minuszeichen weg, weil dr und g entgegengerichtet sind.)
W
= m ⋅ g ⋅ h = ∆E pot
(4)
∆Epot ... Änderung der potentiellen Energie (von 0 auf h)
24
Mechanik – Arbeit und Energie
4.2.
Potentielle Energie
−
r r r
gegeben: Kraftfeld lt. <3.2.>, also F = F( r )
−
r
r
Wenn man die Punktmasse quasistatisch mit der Kraft Fa gegen die Feldkraft F
verschiebt, wird die folgende Arbeit geleistet:
r
r r
r
dW = Fa ⋅ d r = −F ⋅ d r
(5)
r
r
Integration ergibt für den Weg r1 → r2 :
r
r
2 r
r r
r
W ( r1 , r2 ) = − ∫ F d r
r
r1
−
Es zeigt sich, dass diese Arbeit für wichtige Kraftr
r
felder unabhängig vom Weg r1 → r2 ist:
(6)
!
Solche Kraftfelder heißen konservative Kraftfelder oder Potentialfelder.
Beispiele dafür sind die Gravitations- sowie die
elektrostatischen Felder.
Beide gehören zu den Zentralfeldern:
r
r
r
F = f (r ) ⋅
r
å æ
r
F = f (r )
∃ nur Radialkomponente
(7)
Alle Zentralfelder lt. Gl. (7) sind konservativ, und zwar im Prinzip mit beliebigem f(r). In der Realität existieren aber eben nur bestimmte.
−
Wegunabhängigkeit heißt also:
r
r2
r
r
r1
I
r
r2
r
r1
II
r
r1
r r r2 r r
∫ F dr = ∫ F dr
⇒
−
r r
r r
(8)
r r
∫r F dr + r∫ F d r = ∫ F d r = 0
r1
I
(9)
r2
II
Definition: potentielle Energie, Epot
r r
dW = dE pot = − F ⋅ d r
(10)
25
Mechanik – Arbeit und Energie
bzw. in Integralform:
r
r2
r r
r
r
W = − ∫ F d r = E pot ( r2 ) − E pot ( r1 )
(11)
r
r1
r r
Vorzeichenwahl: Bewegung gegen die Feldkraft, d.h. F ⋅ d r < 0 führt zu ∆Epot > 0
bzw. W > 0.
r
r
Bemerkung: r1 und E pot ( r1 ) können dem Problem angepasst frei gewählt werden.
4.3.
−
Feldkraft und potentielle Energie
das totale Differential:
gegeben: Funktion z = f(x,y)
Es gilt:
−
analog im 3D ist Epot = Epot(x,y,z):
⇒
−
dz = (dz )1 + (dz )2
∂z
∂z
dz =
⋅ dx +
⋅ dy
∂x
∂y
á
á
(partielle Ableitungen)
dE pot =
∂E p
∂x
⋅ dx +
∂E p
∂y
⋅ dy +
∂E p
∂z
(12)
andererseits ist lt. Gl. (10):
dE pot = − Fx ⋅ dx − Fy ⋅ dy − Fz ⋅ dz
−
⋅ dz
(10‘)
Gleichsetzung von (10‘) und (12) liefert:
r
r ∂ r ∂ r ∂ 
F = − i
+ j + k E p
∂y
∂z 
 ∂x
r
F = −grad E p = −∇ E p
(13)
mit ∇ ... Nabla-Operator
26
Mechanik – Arbeit und Energie
4.4.
−
Der Energiesatz der Mechanik
r r
Multiplikation von Gl. (13) mit r& = v& :
r r
r
F ⋅ r& = −grad E pot ⋅ r&
 r ∂E pot r ∂E pot r ∂E pot   r dx r dy r dz 
= − i
+j
+k
+j
+k 
⋅ i
∂y
∂z   dt
dt
dt 
 ∂x
d
= − E pot
dt
mit (12):
−
andererseits ist nach dem 2. NEWTONschen Axiom:
r
r
F = m&r&
r r
r r
F ⋅ r& = m&r& ⋅ r&
−
r
| ⋅ r&
Es lässt sich leicht zeigen, dass:
(16)
Der Vergleich von (14), (15) und (16) liefert:
−
d
d
E pot = E kin
dt
dt
bzw.
d
d
E pot + E kin = 0
dt
dt
Die mechanische Energie (= Summe aus Ekin und Epot) ist in einem konservativen Kraftfeld (Potentialfeld) konstant.
−
(3 - 2)
(15)
d
d mr 
E kin =  r& 2 
dt
dt  2 
r r
r r
1
= ⋅ m ⋅ 2 ⋅ &r& ⋅ r& = m&r& ⋅ r&
2
−
(14)
(17)
!
Zur Rolle der Reibung:
Reibung verwandelt Ekin in Wärme (= ungeordnete Teilchenbewegung)
⇒ Verletzung des Energieerhaltungssatzes der Mechanik
!
(Wenn man die Wärmeenergie mit einbezieht, bleibt die Energie natürlich wieder erhalten.)
Reibung stört nicht die Impulserhaltung.
!
27
Mechanik – Gravitation
5.
Gravitation
5.1.
Drehimpuls und Drehmoment
−
Der Drehimpuls tritt bei Drehbewegungen an die Stelle des Impulses. Wir betrachten zunächst den Drehimpuls eines Teilchens (später werden wir den Drehimpuls auch für rotierende starre Körper betrachten):
−
Wir definieren als Drehimpuls bezüglich des Ursprungs 0:
(also:
−
r
r r
L = r×p
r
r r
r r
L = r ⋅ p ⋅ sin( r , p) )
!
(1)
Untersuchung der so definierten Größe:
r
L steht ⊥ auf der Ebene, in der die Drehung erfolgt.
!
„Davonfliegen", keine Drehung um
den Ursprung
r
r r
sin( r , p) = 0 ⇒ L = 0
r r r
r r
sin( r , p) = 1 ⇒ L = r ⋅ p
„maximale Drehung“
⇒
Größe hängt plausibel mit der „Intensität“ der Drehbewegung zusammen!
28
Mechanik – Gravitation
−
Drehimpuls ist eine allgemeine Größe und nicht an die Existenz einer Rotation
gebunden, z.B.:
!
Auch hier existiert ein (konstanter) Drehimpuls:
r r
r
r r
L = p Lok ⋅ r ⋅ sin( p, r )
14243
b
r
r
L = p Lok ⋅ b = const. !
−
r
Änderung von L :
r
r r
dL
d
m ⋅ r × r&
=
dt
dt
r r
r r
= m ⋅ r& × &r + m ⋅ r × &r&
r
r r r
dL
= r×F ≡ M
dt
(
mit:
)
(2)
(3)
M ... Drehmoment
Maßeinheit: [M] = N ž m
SI
Das Drehmoment ist der Kraft beim Impuls analog! Zur Erinnerung:
!
r
r
dp
=F
dt
(3 - 7)
r
Plausibilitätserklärung: M = Kraft × wirksamer Kraftarm
!
Untersuchung der Größe:
r
r r
r × F = 0 , d.h. L = const.
keine Änderung der
„Intensität der Drehung“
29
Mechanik – Gravitation
r r r r
r × F = r ⋅ F → max .
maximale Änderung!
−
Zentralfeld (z.B. Gravitation):
⇒
r r
F~ r
r
r r r
r
dL
= 0 , d.h. L = const.
M = r × F = 0 , d.h.
dt
r
Im Zentralfeld ist L = const. , sofern keine äußeren Drehmomente angreifen.
5.2.
!
Das Gravitationsgesetz
−
Newton 1665/66, „Apfel“
−
Wahrscheinliche Logik der Herleitung:
a) Beobachtung, dass alle Körper gleich schnell fallen
⇒ Beschleunigung, m&x& = Gravitationskraft ~ m des fallenden Körpers
b) Reaktionsprinzip
⇒ gegenseitige Anziehung; Gesetz sollte bezüglich m1 und m2 symmetrisch sein
c) Abstandsabhängigkeit? → Betrachtung der Mondrotation um die Erde:
Für den Mond muss die Gravitationskraft die notwendige Zentripetalbeschleunigung aufbringen;
Zentripetalbeschleunigung lt. Gl. (3 - 15):
2


2π
m
m
a=ω r=
⋅ 6,37 ⋅ 10 6 ⋅ 60 2 = 2,73 ⋅ 10 −3 2

s
s
 27,3 ⋅ 86 400 
â
â
(86400 s/Tag) (Erdradius = 6370 km)
2
r
m
Auf der Erdoberfläche ist g ≈ 9,81 2 , also 3600 Mal größer:
s
9,81
2,73 ⋅ 10
−3
= 3600 = 60 2
⇒
Gravitationskraft fällt mit
1
!
r2
30
Mechanik – Gravitation
⇒
Gravitationskraft
r
m ⋅m
FG = − γ ⋅ 1 2 2
r
r
r
⋅
r
(4)
γ ... Proportionalitätskonstante (Gravitationskonstante)
γ wird experimentell bestimmt (Drehwaage) zu:
γ = (6,6720 ± 0,0004) ž 10-11
−
Nm 2
kg 2
träge und schwere Masse:
Masse verkörpert
·
·
!
die Trägheit (Widerstand gegen Bewegungszustandsänderung) und
sie ist Gegenstand der Gravitationskraft
Dies zunächst zwei verschiedene Dinge!
Fallexperimente:
r
m ⋅M
F = γ ⋅ S 2 = m T ⋅ &x&
r
M ... Erdmasse
mS ... schwere Masse
mT ... träge Masse
Alle Körper haben (innerhalb von 10-12) gleiche Beschleunigung.
⇒
Träge und schwere Masse sind innerhalb dieser Grenzen gleich
(eigentlich proportional zueinander, entsprechende Festlegung von γ, s.o.)
Inzwischen hat Einstein die Gleichheit von träger und schwerer Masse postuliert
und als Grundlage der allgemeinen Relativitätstheorie genommen.
−
Obwohl Gravitation immer eine beiderseitige Anziehung ist, ist es oft zweckmäßig, für eine der Massen das Kraftfeld zu betrachten:
mit:
r
FG
r
r
 γ⋅M r 
= m ⋅− 2 ⋅  ≡ m ⋅G
r
 r
r
G
r
γ⋅M r
=− 2 ⋅
r
r
G ... Gravitationsfeldstärke







(5)
r
r
Also: Zu gegebenem G -Feld ergibt sich Gravitationskraft auf m einfach als m ⋅ G .
31
Mechanik – Gravitation
5.3.
−
Potentielle Energie und Gravitationspotential
Wir wählen in Gl. (4 - 11) r1 = ∞ und bilden:
r
r
r r
1
mM
W = − ∫ Fd r = γmM ∫ 2 dr = − γ
r
∞
∞r
r
(6)
Dies ist gleich Epot(r) - Epot(∞), vgl. (4 - 11).
−
Wenn wir vernünftigerweise Epot(∞) = 0 setzen, folgt
E pot (r ) = − γ
mM
r
(7)
für die potentielle Energie der Masse m im Schwerefeld der Masse M.
r
r
Gravitationspotential: Wir können analog zu FG → G auch Epot in eine munabhängige Größe umwandeln, das Gravitationspotential Φ
−
Es ist definiert:
Φ
also:
=
E pot
m
M
Φ(r ) = − γ
r
(8)
Darstellung:
5.4.
Planetenbewegung
Die KEPLERschen Gesetze (1609/21) lauten:
1.) Die Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne steht.
!
2.) Der Fahrstrahl überstreicht in gleichen Zeiten
gleiche Flächen.
!
3.) Die Quadrate der Umlaufzeiten der Planeten verhalten sich wie die dritten Potenzen der großen Halbachsen.
!
32
Mechanik – Gravitation
zu 1.) Ein Beweis soll hier nicht gegeben werden (geht mit Energiesatz).
Außerdem ist die Exzentrität der Planetenbahnen unseres Sonnensystems gering, die Bahnen sind in sehr guter Näherung Kreise.
Massenverhältnisse:
Erde/Sonne
~
Jupiter/Sonne ~
⇒
1
333 000
1
1 000
(schwerster Planet)
Sonne ruht praktisch
zu 2.) Dies folgt aus der Drehimpulserhaltung:
r
r
r r
r dr
dA
v
L = r × mv = m ⋅ r ×
= 2m ⋅
dt
dt
â
r r
r × d r = Fläche MABC = 2 ž dA
also: Schnell Bewegung in Sonnennähe, langsame in der Ferne
zu 3.) (vereinfachter Beweis für vernachlässigbare Exzentrität) Auch für die Planeten gilt
(analog dem Fall Erde – Mond, vgl. <5.2.>):
Zentripetalkraft ... mω 2 r = γ
mit ω =
mM
... Gravitationskraft
r2
2π
folgt:
T
T2
4π 2
=
= const.
γ⋅M
r3
33
Mechanik – Schwingungen I
6.
Schwingungen I
6.1.
Der Federschwinger
−
Eine Feder setzt ihrer Verformung eine Federkraft entgegen, die der Verformung proportional ist.
FF = −D ⋅ x
mit:
(1)
D ... Federkonstante
Maßeinheit: [D] =
−
!
N
m
SI
Eine an der Feder befestigte Masse wird nach dem Loslassen beschleunigt:
FF = m ⋅ a = m ⋅ &x&
(3 - 2)
⇒ mit (1):
- D ⋅ x = m ⋅ &x&
bzw.
D ⋅ x + m ⋅ &x& = 0
| :m
d2
D
⋅x + 2 x = 0
m
dt
(2)
Dies ist die Bewegungsgleichung des Federschwingers, eine lineare Differentialgleichung 2. Ordnung.
−
Gl. (2) beschreibt den dynamischen Vorgang der Bewegung der Masse. Sie gilt
zu jedem Zeitpunkt t, in allen „Stadien“, z. B. denen maximaler Geschwindigkeit der Masse (= l) oder maximaler Verformung der Feder (= u), aber auch
allen Zwischenstadien:
−
Mathematische Lösung für Gl. (2)? &x& ~ − x ⇒ Es kommen sin- oder cosFunktion in Frage.
!
34
Mechanik – Schwingungen I
⇒
x ( t ) = x 0 ⋅ cos ω0 t
x& ( t ) = − x 0 ω0 ⋅ sin ω0 t
⇒
&x&( t ) = − x 0 ω0 ⋅ cos ω0 t
Ansatz:
2





(3)





(4)
(3) in (2):
⇒
⇒
D
2
⋅ x 0 cos ω0 t − x 0 ω0 ⋅ cos ω0 t = 0
m
D
D !
2
= ω0 , d.h. ω0 =
m
m
Also ergibt sich als Lösung für Gl. (2)
x ( t ) = x 0 cos ω0 t
mit:
D
2π
= 2πν =
T
m
ν ... Frequenz
T ... Schwingungsdauer
ω0 =
ω lt. Gl. (4) ist plausibel:
·
·
straffe Feder/kleine Masse
weiche Feder/große Masse
→
→
schnelle Bewegung
langsame Bewegung
−
Gl. (3) ist auch bezüglich der Anfangsbedingungen x(0) = x0 gut gewählt. Die
Funktion x = x0 sinωt erfüllt die Differentialgleichung (2) ebenfalls, entspricht
aber nicht der Anfangsbedingung. Sie wäre richtig, wenn wir bei x = 0 mit einem „Schubs“ starten! Für „Schubs“ + Auslenkung brauchen wir die allgemeine
Lösung x(t) = x0 [c1 sinω0t + c2 cosω0t] (Linearkombination der beiden unabhängigen Lösungen), die lt. Mathematik hier eigentlich gilt.
−
kinetische Energie:
E kin =
m 2 m 2
v = x&
2
2
(4 - 3)
mit Gl. (4)
⇒
⇒
mit:
x& ( t ) = − x 0 ω0 ⋅ sin ω0 t
m
/
2 D
E kin = x 0
sin 2 ω0 t
2
m
/
E kin =
D 2
x 0 sin 2 ω0 t
2
ω0 =
D
m






(5)
35
Mechanik – Schwingungen I
−
potentielle Energie: vgl. Gl. (4 - 11)
x
W = − ∫ FF dx = E pot ( x ) − E pot (0)
(4 - 11)
0
(W ist die beim Verformen der Feder, also gegen die Federkraft geleistete Arbeit. Epot(0) wird zweckmäßiger Weise gleich Null gesetzt.)
Gl. (1) in (4 - 11):
x
⇒
E pot ( x ) = − ∫ (− D ⋅ x ') dx '
0
=
D 2
x
2
(6)
Gl. (4) in (6):
E pot ( x ) =
mit:
−
ω0 =






D 2
x 0 cos 2 ω 0 t
2
D
m
(7)
Wir haben also ein ständiges „Hin- und Herfluten“ von Ekin ↔ Epot. Die Gesamtenergie ist natürlich konstant:
E ges =
(
)
D 2
x 0 sin 2 ω0 t + cos 2 ω0 t
144424443
2
(6)
=1
−
Schwingungen in Systemen mit |Kraft| ~ Auslenkung (Gl. (1)), die also sinoder cos-Verlauf haben, heißen harmonische Schwingungen.
!
36
Mechanik – Schwingungen I
Sie haben große Bedeutung, weil bei ihnen ja Epot ~ Auslenkung2 ist und sich jedes Potentialminimum als Parabel annähern lässt. Jede Schwingung um irgendein Potentialminimum kann also in gewissem Maße durch eine harmonische
Schwingung angenähert werden.
Ein Beispiel für eine näherungsweise harmonische Schwingung ist das Pendel.
6.2.
−
Das Pendel
Gewichtskraft:
r r
r
G = G || + G ⊥
á á
spannt den Faden wirkt rücktreibend
(9)
Man erkennt leicht, dass
G ⊥ (ϕ) = −G ⋅ sin ϕ
mit G = m ⋅ g folgt
G ⊥ (ϕ) = −m ⋅ g ⋅ sin ϕ
−
Diese Kraft beschleunigt die ausgelenkte Masse:
&&(ϕ)
G ⊥ (ϕ) = m ⋅ &s&(ϕ) = m ⋅ l ⋅ ϕ
−
(11)
(10) und (11) ergibt:
&& = − m
m
/ ⋅l⋅ϕ
/ ⋅ g ⋅ sin ϕ
g
&& + sin ϕ = 0
ϕ
l
−
(10)
(12)
(12) ist nicht mehr exakt lösbar. Wir beschränken uns auf kleine Winkel, dann ist:
ϕ ≈ sin ϕ
und (12) wird zu:
&& +
ϕ
−
g
ϕ=0
l
(13)
Gl. (13) entspricht völlig Gl. (2), das Pendel für kleine ϕ (sogenanntes mathematisches Pendel) vollführt eine harmonische Schwingung mit der Kreisfrequenz:
ω0 =
g
2π
= 2πν =
l
T
(14)
37
Mechanik – Schwingungen I
Kommentar:
− Durch Messung von T und l ist g bestimmbar!
− ω0 ≠ f(m)!

l
 T = 2π ⋅

− langes Pendel ⇒ großes T

g 

6.3.
−
Gedämpfte Schwingungen
Bisher haben wir ungedämpfte Schwingungen betrachtet. In der Realität ∃ Reibung:
⇒ Außer der Federkraft wirkt auch noch eine Reibungskraft, d.h. wir müssen
das NEWTONsche Grundgesetz (Gl. (3 - 2)) ansetzen als:
Fges = FF + FR = m&x&
−
(15)
Die Reibungskraft FR setzen wir wieder v-proportional an lt. Gl. (3 - 19):
⇒
−
u
− D ⋅ x − k ⋅ x& = m&x&
An Stelle von Gl. (2) tritt also:
D
k
x + x& + &x& = 0
m
m
(16)
Exkurs:
Darstellung von Schwingungen mittels komplexer Zahlen
!
P
→ x + iy
x + iy = r[cos ϕ + i sin ϕ]
Betrachtet wird eine Rotation in
der komplexen Ebene
Physikalisch relevant ist natürlich nur der Realteil x(t), also die Projektion auf die x-Achse.
Warum macht man das so kompliziert? → In der komplexen Ebene ist jede Schwingung ist ein rotierender Vektor (Zeiger), die Überlagerung mehrerer Schwingungen
ist einfach die Addition mehrerer Vektoren (Zeiger) zu jedem Zeitpunkt). Haben die
überlagerten Schwingungen gleiches ω0, ergibt sich ein Summenvektor, der mit diesem ω0 rotiert. Wenn man die Addition in der komplexen Ebene vollzogen hat, muss
man auf den Realteil zurückgehen.
Man schreibt:
cos ϕ + i sin ϕ = e iϕ
(17)
38
Mechanik – Schwingungen I
−
Lösung von Gl. (16) auf diese Weise:
Wir setzen als Lösung für Gl. (16) an: x = x 0 e λt ⇒ x& = λx 0 e λt , &x& = λ2 x 0 e λt
Dies in Gl. (16) eingesetzt:
⇒
⇒
D k

x 0 e λt  + λ + λ2  = 0
m m

á
á
≠ 0 ∀t
q + pλ + λ2 = 0
(18)
Wir müssen nur die quadratische Gleichung lösen1 und erhalten:
2
λ1, 2 = −
−
k
D
 k 
± 
 −
2m
m
 2m 
(19)
Wir betrachten den Fall relativ geringer Dämpfung (d.h., es soll überhaupt noch
eine Schwingung stattfinden). Dann ist der Radikand negativ:
2
D
 k 
 − <0

m
 2m 
Umformung entsprechend dem physikalisch allein sinnvollen ω2 > 0 ergibt:
λ1, 2 = −
 D  k 2 
k
2
± − −
  = −δ ± − ω
m
2
m
2m

 

(20)
⇒
λ 1 = − δ + iω
⇒
x̂ = x 0 e ( − δ+iω) t
(21a)
⇒
λ 2 = − δ − iω
⇒
x̂ = x 0 e ( − δ−iω) t
(21b)
Beide Gleichungen führen, wenn wir den Realteil bilden, auf dasselbe, nämlich
x = x 0 e −δt ⋅ cos ωt
(22a)
Anders als Gl. (4) klingt die Schwingung mit e-δt ab, wobei lt. Gl. (20) gilt:
δ=
k
2m
(22b)
D.h. schnelles Abklingen für großes k, also großes FR, sowie kleines m!
1
Lösungsformel:
λ 1, 2 = −
p
±
2
p2
−q
4
39
Mechanik – Schwingungen I
Ferner ist
ω=
D
− δ2 ,
m
d.h., die Frequenz ω ist gegenüber der Frequenz ω0 =
−
(22c)
D
reduziert.
m
Im Grenzfall verschwindet die Wurzel in Gl. (20), d. h.:
2
D
 k 
 − =0

m
 2m 
Dadurch vereinfacht sich die Lösung zu:
⇒
λ 1 = λ 2 = −δ
Es lässt sich zeigen, dass die allgemeine Lösung dann lautet:
x = x 0 (1 + δ ⋅ t ) ⋅ e −δt
Dies ist der sogenannte aperiodische Grenzfall, d.h. das schnelle Einschwenken
in die Nulllage.
−
(23)
!
Für noch stärkere Dämpfung folgt entsprechend:
2
D
 k 

 − >0
m
 2m 
Hier kann man von Schwingung nicht mehr sprechen. Die Auslenkung geht
ebenfalls asymptotisch gegen Null, aber langsamer als lt. Gl. (23). Dies ist der
sogenannte Kriechfall
!
40
Mechanik – Systeme von Massenpunkten; Stöße
7.
Systeme von Massenpunkten; Stöße
7.1.
Der Schwerpunkt
−
r
Wir definieren den Schwerpunkt rs eines Systems:
r
∑ m i ri
r
rs = i
∑ mi
=






r
1
m i ri
∑
M i
i
mit:
M = ∑ m i ... Gesamtmasse
i
(1)
Veranschaulichung:
r 1 r
r
rs = ( r1 + 2 r2 )
3
−
aus (1) folgt:
⇒
r
r
M ⋅ rs = ∑ m i r
|
i
r
r
r
r
M ⋅ r&s = p s = ∑ m i r&i = ∑ p i
i
d
dt
(2)
i
Der Gesamtimpuls des Systems ist das Produkt aus Gesamtmasse und Schwerpunktgeschwindigkeit.
−
!
nochmalige Differentiation von (2) ergibt:
⇒
r
r
r
r
r
M ⋅ &r&s = p& s = Fs = ∑ m i &r&i = ∑ Fi
i
i
(3)
Der Schwerpunkt bewegt sich so, als wenn dort die Summe aller Einzelkräfte an
der Gesamtmasse angreifen würde.
!
r
r
Also: Keine äußere Kraft, d.h. Fs = ∑ Fi = 0 ⇒ Schwerpunkt bewegt sich
!
i
gleichförmig, oder (Sonderfall) ruht.
Mit anderen Worten: Gesamtimpuls im abgeschlossenen System = const.
41
Mechanik – Systeme von Massenpunkten; Stöße
r
oder: ∃ äußere Kräfte Fi , dann ergänzen sich diese in ihrer Wirkung so, als ob
r
r
Fs = ∑ Fi am Schwerpunkt angreifen würde.
!
Beispiel:
n
i
Geworfene Hantel:
Letzteres gilt auch dann, wenn innere Kräfte auftreten:
Beispiel:
n
Explodierende Granate:
Die inneren Kräfte zwischen den Bruchstücken ergänzen sich jeweils zu Null
(Actio = Reactio!), der Schwerpunkt folgt seiner eigenen Trägheit sowie der
Erdbeschleunigung und bewegt sich weiter auf der Wurfparabel.
7.2.
Stöße: Grundlagen
−
Stöße = gegenseitige Ablenkung von sich bewegenden Teilchen
−
hier: Experimente meist mit harten Kugeln
−
Bedeutung der Stöße jedoch besonders wichtig für die Atomphysik, wo die Ablenkung entsprechend dem Kraftfeld bzw. dem Wechselwirkungs-Potential allmählich erfolgt.
Beispiel:
!
n
Coulombablenkung eines e- an einem Atomkern
42
Mechanik – Systeme von Massenpunkten; Stöße
r
dann: Betrachtung der asymptotischen Größen p , Ekin weit vor bzw. weit nach
der Wechselwirkung
−
Im abgeschlossenen System1 gilt beim Stoß von 2 Partnern:
r r
r r
p1 + p 2
=
p1′ + p′2
m1 r 2 m 2 r 2
m1 r 2 m 2 r 2
v1 +
v2 =
v1′ +
v ′2 + Q
2
2
2
2
(vor)
(nach)
Impulssatz
(4)
Energiesatz
(5)
Q ist die gegebenenfalls anderweitig verbrauchte Ekin (z.B. Verformungsenergie)
⇒ elastischer Stoß, Ekin bleibt erhalten,
⇒ inelastischer Stoß, Ekin, ges wird durch Stoß reduziert.
Q=0
Q>0
7.3.
Elastische Stöße im Laborsystem
−
Laborsystem = das Bezugssystem, in dem wir uns befinden (also eigentlich das
naheliegende)
−
Wir betrachten zunächst zentrale Stöße
(⇒ 1D-Problem)
−
Zur Beschreibung dient die Impulserhaltung (Gl. (4))
und die Energieerhaltung (Gl. (5) mit Q = 0)
−
Wir betrachten den Sonderfall, dass der gestoßene Körper vor dem Stoß ruht:
m1 v1 = m1 v1/ + m 2 v 2/
m 1 2 m1 / 2 m 2 / 2
v1 +
v2
v1 =
2
2
2
!
(4′)
(5′)
Umordnung von (4′) und (5′):
⇒
m 2 v 2/ = m1 ( v1 − v1/ )
⇒
2
m 2 v 2/
(5' ' )
( 4' ' )
⇒
bzw.
1
= m 1 ( v1 2 −
2
v1/ )
(4″)
= m1 ( v1 − v1/ )( v1 + v1/ )
(5″)
:
v1 + v1/ = v 2/
v1/ = v 2/ − v1
(6 )
(6′)
d.h., wenn man alles einbezieht, was dazu gehört.
43
Mechanik – Systeme von Massenpunkten; Stöße
(6) in (4′):
⇒
⇒
m1 v1 = m1 v1/ + m 2 ( v1 + v1/ )
m − m2
v1/
= 1
⋅ v1
m1 + m 2
(7)
(6′) in (4′):
⇒
⇒
m1 v1 = m1 ( v 2/ − v1 ) + m 2 v 2/
2m1
v 2/
=
⋅ v1
m1 + m 2
(8)
Sonderfälle:
(1)
m1 = m2
⇒ v1/ = 0 ;
−
v 2/ = v1
(2)
m1 = 2m2, also stoßender Körper doppelt so schwer
1
4
⇒ v1/ = v1 ; v 2/ = v1
3
3
stoßender Körper läuft gestoßenem (langsamer) hinterher
(3)
m1 = m2/2, also stoßender Körper halb so schwer
1
2
⇒ v1/ = − v1 ; v 2/ = v1
3
3
stoßender Körper läuft rückwärts!
(3′)
m1 << m2, also „Stoß gegen die Wand“
⇒ v1/ = − v1 ; v 2/ ≈ 0
Trotzdem bleibt der Gesamtimpuls unverändert = m1v1, d.h., m2 bewegt
sich schon in v1-Richtung, aber eben sehr langsam. Dennoch ergibt sich
wegen des großen m2 der richtige Impuls.
Energieübertrag auf m2: Ist für m1 = m2 maximal, d.h. vollständig, für alle anderen Fälle geringer. Genauer mit (8):
(Terminologie: E ′kin , 2 ... kinetische Energie von m2 nach dem Stoß)
m 2 / 2 m 2 ( 2m 1 ) 2
v2 =
⋅ v1 2
2
2
2 ( m1 + m 2 )
m
4 m1 ⋅ m 2
= 1 v1 2 ⋅
223 (m1 + m 2 ) 2
1
E ′kin , 2 =
E ′kin , 2 = E kin ,1
⋅
4 m1 ⋅ m 2
( m1 + m 2 ) 2
(9)
44
Mechanik – Systeme von Massenpunkten; Stöße
⇒
⋅
Verhältnis der Massen entscheidend (m1 = n ž m2 und
1
ž m2 liefern
n
gleiches Ergebnis)
⋅
−
7.4.
Übertragung beliebig klein:
1
bzw. 2
2
1
bzw. 100
100
⇒ 89 %
⇒ 4%
Wichtig für Teilchenphysik (Abbremsung), z.B. Neutronenmoderierung
Stöße im Schwerpunktsystem
−
Schwerpunktsystem = System, in dem der Schwerpunkt ruht. Günstig, wenn die
gestoßene Masse vor dem Stoß nicht ruht.
−
Gl. (2) war:
r
r
r
M ⋅ vs = ps = ∑ pi
(2)
i
r
Wenn der Schwerpunkt also ruht ( v s = 0 ) muss
!
r
∑ p i = 0 sein.
i
n
Beispiel:
elastischer Stoß zweier Teilchen
vorher:
p1 + p 2 = 0
nachher:
p 1′ + p ′2 = 0
p1′ = − p1
p ′2 = − p 2
−
Also: Problem im Schwerpunktsystem einfach zu behandeln!
−
Man muss natürlich alle Bewegungen wieder ins Laborsystem zurücktransformieren. Da sich aber in abgeschlossenen Systemen der Schwerpunkt geradlinig
gleichförmig bewegt, ist das einfach.
7.5.
!
Inelastische Stöße
−
Ein Teil der Ekin wird aufgezehrt (Wärme, Verformung, ...) → keine EkinErhaltung mehr
−
Dennoch wird die Abbremsung begrenzt, da der Impuls erhalten bleiben muss.
45
Mechanik – Systeme von Massenpunkten; Stöße
⇒ Was ist das Maximum der Umwandlung von Ekin in Q?
Schwerpunktsystem: Im Schwerpunktsystem ist die Summe aller Impulse = 0
(s.o.). Dies kann auch erfüllt werden, indem alle Teilchen
im Schwerpunktsystem zur Ruhe kommen.
vorher:
p1 + p 2 = 0
nachher:
p1′ + p ′2 = 0
r
r
Der Gesamtimpuls ist nach wie vor der des Schwerpunktes, also M ⋅ v s = p s lt. Gl. (2)!
⇒
Die maximal mögliche Abbremsung, ohne den Impulssatz zu verletzen, ist
das völlige Zur-Ruhe-Kommen im Schwerpunktsystem.
!
Mit anderen Worten:
Alle beteiligten Teilchen bleiben aneinander kleben und bewegen sich mit
einer gemeinsamen Geschwindigkeit, der des Schwerpunktes.
7.6.
Nichtzentrale Stöße
−
... bringen physikalisch nichts grundsätzlich Neues, man muss das Problem lediglich mehrdimensional (es ist 2D) lösen. Beispiel Stoß in x-Richtung:
−
α ist geometrisch determiniert:
sin α =
−
d
r1 + r2
(r1, r2 ... Kugelradien)
β stellt sich so ein, dass pges,y weiterhin gleich Null ist, d.h.
p ′2, y − p1′, y = 0
−
r
r r
Ansonsten muss der Gesamtimpulses erhalten bleiben ( p1 = p1′ + p′2 ) sowie gegebenenfalls (elastisch - inelastisch) die kinetische Energie.
46
Mechanik – Bewegte Bezugssysteme
8.
Bewegte Bezugssysteme
8.1.
Vorbemerkungen
−
Die grundlegenden Gesetze der Mechanik haben wir bisher ohne Bezug auf ein
spezielles Bezugssystem definiert. Grundgesetze sollen ja auch unabhängig
vom Bezugssystem gelten!
−
Wir betrachten im Folgenden:
·
Bezugssysteme mit konstanter Relativgeschwindigkeit u << c
·
Linear beschleunigte Bezugssysteme
·
Rotierende Bezugssysteme
−
Die Relativitätstheorie ist nicht Gegenstand dieses Kapitels.
8.2.
−
−
Bezugssysteme mit konstanter Relativgeschwindigkeit u << c
−
}
< 10-4 ž c
betrachtet werden nun die Systeme S und S‘:
Ortsvektor in S‘:
Ortsvektor in S:
−
n
Beispiel:
Mach-3-Düsenjäger 3600 km ž h-1
=
1 km ž s-1
Erdsatellit
=
8 km ž s-1
u << c bedeutet also in der Regel keine ernste Einschränkung!
r
r′
r
r
r r
r
= r0 + u ⋅ t + r ′
r
Transformation mit konstantem u ≡ Galilei-Transformation
Geschwindigkeit in S‘:
Geschwindigkeit in S:
r
v
r
v′



(1)
!
r
r
d r0 d (u ⋅ t ) r&
=
+
+ r′
dt
dt
r
r
r
=0 +u
+ r& ′
47
Mechanik – Bewegte Bezugssysteme
bzw.
r
v
r r
= v′ + u
r
p
r r
= p′ + u ⋅ m



(2)
Also einfacher additiver Zusatzterm, der Impulserhaltung nicht beeinträchtigt.
−
Beschleunigung in S‘:
r
a′
Beschleunigung in S:
r
a
also
r
r
d 2 r ′ dv ′
=
dt
dt 2
r
2r
d r dv
= 2 =
dt
dt
r
r
dv′ du
=
+
dt
dt
r
dv ′
=
+0
dt
=
r
a
r
dv ′ r
=
= a′
dt
(3)
r
F′
r
r r
= m ⋅ a = m ⋅ a ′ = F′
(4)
⇒ Alle Galilei-transformierten Systeme sind in der Beschreibung der physikalischen Gesetze äquivalent. Die Gesetze der klassischen Mechanik sind Galileiinvariant. Die Gesamtheit der Galilei-transformierten Systeme heißt Inertialsysteme.
8.3.
−
!
Linear beschleunigte Bezugssysteme
r
System S‘ bewege sich nun beschleunigt mit a s relativ zum S:
Ortsvektor in S‘:
Ortsvektor in S:
r
r′
r
r
r
r as 2 r
r
= r0 + t + u ⋅ t + r ′
2
−
wir fragen nach den Beschleunigungen in beiden Systemen:
−
Beschleunigung in S‘:
Beschleunigung in S:
bzw.
r
a′
r
a
r
= &r&′
r
= &r&
r
r
r
d 2 r0 d 2 (u ⋅ t ) d 2  a s 2  &r&
= 2 +
+ 2  t  + r′
dt
dt 2
dt  2 
r
r
=0
+0
+ as
+ a′
r
a
r r
= a s + a′
r
a′
r r
= a − as



(5)



(6)
48
Mechanik – Bewegte Bezugssysteme
−
multipliziert mit m:
r
r
r
m ⋅ a′ = m ⋅ a − m ⋅ a s
â
â
r
r
r
F′
= F + Ftr
r
r
Ftr = − ma s ... Trägheitskraft
− Kraft in S‘:
mit:



(7)
Die Trägheitskraft spürt man nur im beschleunigt bewegten System. Für sie ist
dort keine materielle Ursache (wie z. B. Feder, Gravitation, Triebwerk) zu err
kennen, sie rührt nur von a s her.
Man muss sie aber berücksichtigen, damit im beschleunigten Bezugssystem (wo
dieses Beschleunigung nicht existiert) "die Mechanik wieder stimmt". Ohne diese „Scheinkräfte“ wäre dies nicht der Fall.
⇒ Beschleunigte Bezugssysteme sind keine Inertialsysteme.
Beispiel:
startendes Flugzeug:
8.4.
ruhender Beobachter
Beobachter in Kabine
→
→
!
n
Triebwerk "schiebt"
keine Ursache für die Kraft!
Rotierende Bezugssysteme
−
Beobachter B (ruhend):
−
Beobachter A (mitbewegt): Für ihn ruht die Masse! Sie wird durch eine für ihn
unerklärliche Kraft nach „außen“ gezogen, welche
durch die Federkraft kompensiert werden muss, weil
sonst die Masse an die Außenwand geschleudert
würde.
−
Diese „unerklärliche Kraft“, die nur im rotierenden Bezugssystem wirkt, ist die
Zentrifugalkraft. Sie ist betragsmäßig
gleich der Zentripetalkraft (lt. Gl. (3 - 15)),
r
aber nach außen gerichtet (~ r ).
r
r
FZF = mω 2 r
Auf m wirkt ständig die Federkraft FF, die die Masse
auf die Kreisbahn zwingt, indem sie eine ständige
r
Änderung der Richtung von v hervorruft (Zentripetalkraft, -beschleunigung (vgl. <3.6.>)).
!
(8)
49
Mechanik – Bewegte Bezugssysteme
Im allgemeinen Fall, d. h. „r nicht ⊥ ω“,
erhält man:
r
r r r
FZF = m ⋅ ω × ( r × ω)
(8‘)
Zentripetalkraft bewirkt eine Beschleunigung im Laborsystem, Zentrifugalkraft
kompensiert im rotierenden System (wo es keine Bewegung gibt) die Federkraft.
n
Beispiel:
Gezeitenkräfte
−
Erdrotation um sich selbst ist hier unerheblich, da sie die „Normalgestalt“ der Erde
(Abplattung, usw.) bestimmt.
−
Erde und Mond rotieren um den gemeinsamen Schwerpunkt S, der noch innerhalb der Erde liegt:
·
·
·
·
Für M kompensieren sich Anziehung durch den Mond und Zentrifugalkraft genau.
Bei A ist Anziehungskraft kleiner und Zentripetalkraft größer ⇒ „Wasserberg“
Bei B ist Anziehungskraft größer und Zentripetalkraft kleiner ⇒ „Wasserberg“
Wenn „Anziehung des Mondes“ alleinige Ursache wäre, dürfte bei A kein Flutberg
auftreten!
−
Wir kehren zur rotierenden Masse zurück und knipsen jetzt die Feder durch:
−
ruhender Beobachter :
Masse fliegt geradlinig gleichförmig weiter (A‘, B‘, C‘, ...)
50
Mechanik – Bewegte Bezugssysteme
−
−
bewegter Beobachter:
Masse fliegt radial nach außen (A → A‘, B → B‘), da
ja nun die Gegenkraft der Feder fehlt - zunächst!
genauere Betrachtung:
Masse fliegt nicht geradlinig, sondern die Bahnkurve ist im
rotierenden Bezugssystem gekrümmt (C → C‘, D → D‘, ...)
Im rotierenden Bezugssystem muss man die Krümmung der Bahnkruve auf eine
Kraft zurückführen, damit die Mechanik wieder stimmt ⇒ Corioliskraft
r
r r
Fc = 2m ⋅ (v′ × ω)
r
v ′ ... Geschwindigkeit im bewegten System!
−
!
(9)
Bei einem „Schuss || zur Drehachse“ ist die Corioliskraft also Null.
51
Mechanik – Der starre Körper; Rotation I
9.
Der starre Körper; Rotation I
9.1.
Einleitung
−
bisher:
(Systeme von) Punktmassen
−
jetzt:
Betrachtung ausgedehnter Körper, über die die Masse gleichmäßig
verteilt ist (keine Atome!). Körper soll sich unter äußerer Kraft nicht
verformen → starrer Körper
−
Dichte ρ:
ρ=
Maßeinheit:
−
∆m
∆V
[ρ] =
(1)
kg
m3
SI
Gesamtmasse M:
M = ∑ ρ i ∆Vi
i
M=
∫ ρ dV
Vol
−
!






(2)







(3)
r
Ortsvektor des Schwerpunktes S rs :
analog zu Gl. (7 - 1) schreiben wir:
r
r
1
rs =
r dm
∫
M Masse
r
1 r r
rs =
∫ r ⋅ ρ(r ) dV
M Vol
52
Mechanik – Der starre Körper; Rotation I
9.2.
−
Kräfte und Drehmoment an starren Körpern
Wiederholung zum System mehrerer Punktmassen (vgl. <7.1.>):
r
Kraft F greife an Schwerpunkt S eines starren Körpers der Masse M an:
⇒ Bewegung des Körpers gemäß:
r
r
F = M⋅a
−
(3 - 2)
r
Kraft F1′ greife nicht am Schwerpunkt S an:
r
r
r
F1 = F2 = F3
r
r
F2 + F3 = 0
r r r r r
F1′ = F1 = F1 + F2 + F3
123
(4)
â â
Kräftepaar Kraft, die an Schwerpunkt angreift
⇒ Translation, kein Drehmoment
−
Kräftepaar = Paar zweier entgegengesetzt gleicher Kräfte, die an zwei verschiedenen Punkten (hier: S, P) angreifen ⇒ Drehmoment, und zwar:
r r
r
M = rsp × F1
(M hier bezogen auf S)
!
(5)
⇒ „Nicht-Schwerpunkt-Kraft“ bewirkt Translation und Rotation!
„Reines Kräftepaar“ bewirkt nur Rotation.
−
9.3.
r
r
Damit ein Körper in Ruhe bleibt, müssen sowohl Fges = 0 als auch M ges = 0
sein. Dann gibt es weder Translation noch Rotation.
!
Trägheitsmoment
−
gegeben: um bestimmte Achse rotierender Körper
−
gesucht: Ekin der Rotation
53
Mechanik – Der starre Körper; Rotation I
−
kinetische Energie eines Volumenelementes ∆Vi im (senkrechten) Abstand ri
von der Achse ist
∆m i 2
⋅ vi
2
â
Tangentialgeschwindigkeit von mi
∆E kin =
∆m i = ρ i ∆Vi
v i = ω ⋅ ri
â
Winkelgeschwindigkeit
m 2
v gilt natürlich weiterhin. Wir formen nur zweckmäßig um und erhalten
2
ρ i ∆Vi 2 2
⋅ ω ri
2
ω2
=
⋅ ∑ ρ i ∆Vi ri2
2 i
∆E kin =
E kin
bzw. in Integralform:
=
E kin
−
ω2
2
∫r
2
⋅ ρ dV
(6)
Volumen
Die Größe
J
=
∫r
2
ρ dV
(7)
Volumen
heißt Trägheitsmoment.
−
Mit J ergibt sich Ekin dann als
E kin =
J 2
ω
2
(8)
{v} → {ω}
{m} → {J}
−
Analogien:
−
Rotierender Körper lässt sich schwer in Drehung versetzen (d.h. ist träge) bzw.
hat drehend viel Energie, wenn J groß ist, d.h. die gegebene Masse „außen sitzt“.
−
Beispiel:
n
Berechnung von J für homogenen Zylinder (ρ = const.) mit der Länge L:
dV = ds ⋅ dr ⋅ dz
ds = r ⋅ dϕ
54
Mechanik – Der starre Körper; Rotation I
aus (7) folgt damit:
R
J = ρ∫
0
2π
L
∫ ∫r
0
2
⋅ r dr dϕ dz
0
R4
⋅ 2π ⋅ L
4
M = ρ ⋅ V = ρ ⋅ πR 2 L
J =ρ⋅
mit:
1
MR 2
2
MV 1
J =
⋅
2π L
J =
bzw.
Also:
−
(9)
(9‘)
Bei gegebener Masse bzw. (ρ = const!) Volumen kann über R bzw. L das J beliebig zwischen 0 und ∞ eingestellt werden (Draht bis „∞ ausgedehnte Platte“)!
STEINERscher Satz:
gegeben: J um Achse, die durch den
Schwerpunkt geht (≡ Js)
gesucht: J um Achse, die um die
Strecke a von S entfernt ist
(≡ Ja)
Ja = Js + M ⋅ a 2
(10)
Plausibilitätserklärung:
Rotation um „a-Achse“ ⇒ Bewegung des
Schwerpunktes um diese + Rotation des
Körpers um die Schwerpunktachse
9.4.
Dynamik bei der Rotation
9.4.1.
Bewegungsgleichung
−
Für die Translation war (vgl. <3.3.>):
r
dp
=
dt
(3 - 6)
r
r
r
r
F = m ⋅ a = m ⋅ v& = m ⋅ &r&
(3 - 2)
r
F
bzw.
55
Mechanik – Der starre Körper; Rotation I
−
Analog ergibt sich für die Rotation:
r
M
r
dL
=
dt
(5 - 3)
bzw. für J = const. unter Verwendung von α, ω, ϕ (vgl. <2.4.>):
r
r
r&
&r&
M = J⋅α = J ⋅ω
= J⋅ϕ
−
(11)
In völliger Analogie zur Translation gibt es nun die verschiedenen Bewer
gungstypen, z.B. gleichmäßig beschleunigte Drehbewegung mit konstantem M
r
r
und α (was zu linear ansteigendem ω führt), usw.
9.4.2.
Drehschwingungen (1D)
−
...ist dem Federschwinger völlig analog (vgl. <6.1.>)
−
Verformung eines Torsionsstabes führt zu entgegenwirkendem Drehmoment
M T = −D* ⋅ ϕ
mit:
Maßeinheit:
−
(12)
D* ... Richtmoment, [D*] = N m
[D*] = N ž m (= Federkonstante)
SI
(12) in (11) liefert als Bewegungsgleichung:
&& = − D * ⋅ ϕ
J⋅ϕ
(13)
völlig analog zur Gl. (6 - 2) für den Federschwinger!
−
Als Lösung folgt, wieder analog (diesmal zu Gl. (6 - 4)):
ϕ( t ) = ϕ 0 cos ω0 t
mit:
ω0 =





D*
2π
= 2πν =
J
T
Also: steifer Stab/kleines J
nachgiebiger Stab/großes J
(14)
→ schnelle Schwingung
→ langsame Schwingung
Diese Torsionsschwingung ist harmonisch.
−
Auch die gedämpfte Schwingung ist völlig analog.
56
Mechanik – Der starre Körper; Rotation I
9.4.3.
−
Drehimpulserhaltung
Drehimpuls eines Volumenelementes eines rotierenden Körpers:
r
L
r r
= r×p
(5 - 1)
r
r r
∆L = ∆m ⋅ r × v
Wegen v ⊥ r rechnen wir skalar weiter:
∆ L = ∆m ⋅ r ⋅ v
v
= ω⋅ r
∆m = ρ∆V
∆ L = ωr 2 ρ∆V
−
(15)
Gl. (15) gilt für ein Volumenelement eines Körpers. Für den Gesamtkörper müssen wir aufsummieren:
L = ω∑ ri2 ρ i ∆Vi
i
bzw. integrieren:
L =ω
∫r
2
ρ dV
(16)
Volumen
â
≡J
Vergleich mit (7) zeigt, dass (wir schreiben wieder als Vektoren)
r
r
L = ω⋅ J
−
r
Natürlich ist weiterhin gültig, dass für M = 0
System), und zwar
wegen
−
(17)
ist.
r
L = const. ist (abgeschlossenes
r
r
dL
M =
dt
Dies gilt, analog zur Impulserhaltung, unabhängig von eventuellen inneren Reibungskräften.
!
(5 - 3)
!
57
Mechanik – Der starre Körper; Rotation I
9.5.
Zusammenstellung wichtiger formaler Analogien
−
Ortsvektor:
r
r
Drehwinkel:
ϕ
−
Geschwindigkeit:
r r
v = r&
Winkelgeschwindigkeit:
r
ω
⋅ Betrag
ω = ϕ&
⋅ Richtung
Drehachse (Recht-Hand-Regel)
−
Beschleunigung:
r r
a = v&
Drehbeschleunigung:
r r&
α=ω
−
kinetische Translationsenergie:
m
E trans = v 2
2
kinetische Rotationsenergie:
J
E rot = ω 2
2
−
Masse:
m
Trägheitsmoment:
J = ∫ r 2 ρ dV
−
Kraft:
r
F
Drehmoment:
r
M
−
Impuls:
r
r
p = m⋅v
Drehimpuls:
r
r
L = J⋅ω
−
Bewegungsgleichung:
r v
r
F = p& = m ⋅ v&
Bewegungsgleichung:
r r&
r&
M = L = J⋅ω
−
r
r
Im abgeschlossenen System bleiben p und L erhalten
58
Mechanik – Rotation II
10.
Rotation II
10.1.
Trägheitstensor
−
bisher:
r
r
L = J⋅ω
mit:
J
(9 - 17)
= ∫ r 2 ρ dV
(9 - 7)
r r
J war bezogen auf eine bestimmte Achse (mit Abstand r von dieser) und skalar, L ~ ω .
Achse war
fest zum Körper („aufgespießt“) (a), und
fest im Raum („gelagert“)
(b).
−
Jetzt werden (a) und (b) in Frage gestellt.
−
Aufhebung v. (a): freie Rotation eines Quaders →
∃ stabile + instabile Achsen
r
Aufhebung v. (b): Fahrradkreisel ∧ Momentanstoß → Präzession von ω ,
r
L weiter const.
Illustration Handel ⇒ J = f(Achsenrichtung)!
−
weiter mit Plausibilitätserklärung:
Es zeigt sich, dass es nicht ausreicht, einfach nur für jede Achsenrichtung ein
anderes (skalares) J zu nehmen. J ist kein Skalar mehr, auch kein richtungsabhängiger!
!
Im allgemeinen Fall ist J ein Tensor: J
!
r
r
L = J⋅ω
−
(1)
Multiplikation eines Tensors mit einem Vektor ergibt einen neuen Vektor:
r
r
Dies ist eine Transformation bezüglich Betrag und Richtung, d.h. ω und L sind
nicht mehr proportional!
−
!
verwendete Komponentenschreibweise in kartesischen Koordinaten:
r
r
r
r
r
r
r
L = L x + L y + L z = L x i + L y j + L z k ≡ (L x , L y , L z )
In dieser Schreibweise wird (1) zu:
 J xx

(L x , L y , L z ) =  J yx

 J zx
J xy
J yy
J zy
J xz   ω x 
  
J yz  ⋅  ω y 

J zz   ω z 
(2)
59
Mechanik – Rotation II
−
zum Glück ist J ein symmetrischer Tensor:
J xz 

J yz 

J zz 
(3)
Wenn wir das Bezugssystem auf den Körper beziehen (körperfestes Bezugssystem) lässt sich immer eines finden, in dem sich der Tensor noch mehr vereinfacht (In diesem System gelten statt x, y, z die Achsen 1, 2, 3):
!
 J xx

J =  J xy

 J xz
−
 J1

J =0
0

J xy
J yy
J zy
0
J2
0
0

0
J 3 
(4)
Diejenigen Achsen, für die das gilt, heißen Hauptträgheitsachsen.
J1, J2, J3 heißen Hauptträgheitsmomente.
!
Im Allgemeinen sind die Hauptträgheitsmomente ungleich. Wir setzen: J1 ≤ J2 ≤ J3.
10.2.
−
Trägheitsellipsoid
Erot war:
E rot =
−
(9 - 8)
wenn J ein Tensor ist, müssen wir schreiben:
E rot =
−
1 2
Jω
2
r
1r
ω⋅ J ⋅ω
2
â
r
≡ L (lt. Gl.(9 - 14))
(5)
r
Wir beziehen jetzt auch ω auf das körperfeste Bezugssystem mit den Achsen 1, 2, 3:
r r
r
r
r
r
r
ω = ω1 + ω 2 + ω3 = ω1e1 + ω 2 e 2 + ω3 e 3 ≡ (ω1 , ω 2 , ω3 )
(6)
Aus (5) folgt damit:
E rot
 J1

1
= (ω1 , ω 2 , ω3 ) ⋅  0
2
0

0
J2
0
0   ω1 
  
0  ⋅  ω2 
J 3   ω3 
(7)
60
Mechanik – Rotation II
ausmultipliziert folgt:
E rot =
−
)
(8)
Gl. (8) ist die Bestimmungsgleichung für ein Ellipsoid! (8) lässt sich umformen:
E rot =
a=
mit:
−
(
1
J1ω12 + J 2 ω 22 + J 3 ω32
2
1









1  ω12 ω 22 ω32 
+
+
2  a 2 b 2 c 2 
, b=
1
, c=
1
J1
J2
J3
a, b, c ... Hauptachsen des Ellipsoids
(9)
Anschaulich: Der Ellipsoid gibt bei gegebenen Trägheitseigenschaften (d.h.
r
gegebenem Trägheitstensor) für jede Richtung an, wie groß ω sein muss, um
einen bestimmten konstanten Erot-Wert zu erreichen.
!
Beispiel:
n
Rotation um 3 hat großes J (J3 = Jmax) ⇒ ω3 kann klein sein
Rotation um 1 hat kleines J (J1 = Jmin) ⇒ ω1 muss groß sein



für bestimmtes Erot
−
(In der Regel wird versucht, die Form des Ellipsoids aus den Trägheitseigenschaften heraus zu erklären. Dies ist aber ziemlich verwickelt wegen
1
a , b, c =
).
J1, 2,3
−
Also: ∃ 3 ausgezeichnete Achsen, davon einem mit Jmax, eine mit Jmin, diese ⊥
aufeinander. Für alle anderen Richtungen hochsymmetrisches Verhalten,
r
so, dass alle ω für ein bestimmtes Erot ein Ellipsoid formen.
!
Dies gilt für alle starren Körper! (anschaulich schwer einleuchtend)
−
r
r
Wir bilden L = J ⋅ ω in Komponentenschreibweise lt. Gl. (7), multiplizieren aus
und erhalten
r
r
r
r
L = J 1ω1 + J 2 ω 2 + J 3 ω3
(10)
61
Mechanik – Rotation II
r r
⇒ Für unterschiedliche J1, J 2, J3 kann L ~ ω nur erreicht werden, wenn
Rotation um eine der drei Hauptachsen erfolgt
−
Also:
Entweder
oder
oder
−
r r
ω = ω1
⇒
r
r
L = J1 ⋅ ω
r r
ω = ω2
r r
ω = ω3
⇒
r
r
L = J2 ⋅ ω
r
r
L = J3 ⋅ ω
⇒
Dabei ist die Rotation um die Achse mit:
maximalem J (hier J3)
→ stabil
·
minimalem J (hier J1)
→ mäßig stabil
·
mit mittlerem J (hier J2) → instabil
!
·
−
r
r
Wenn ω und L nicht mehr || sind, gibt es Probleme:
r
r
a) freie Rotation: L = const. ⇒ ω ändert sich ständig (relativ zum Körper)
b) Rotation mit
r
r
fixierter Achse: ω = const ⇒ L ändert sich ständig und erzeugt ein
Drehmoment, das die Lager beansprucht:
r
r
dL
M =
>0
dt
⇒ Unwucht
10.3.
Symmetrischer Kreisel
−
Kreisel = rotierender Körper, symmetrisch1, Rotation erfolgt um Achse durch
Schwerpunkt, Lagerung reibungsfrei2. (Dies ist keine strenge Definition!)
!
−
kardanisch gelagerter Kreisel = reibungsfrei im Schwerpunkt gelagert (Geronimo Cardano, 1501 - 1576).
!
−
Nutation: Wir betrachten einen Kreisel, der um seine Figurenachse, die das
maximale J besitzt, rotiert:
!
r r
FA || L || ω ≡ z-Achse
Für den Drehimpuls gilt:
r r
r
r
L = L z = J || FA ⋅ ω z = J max ⋅ ω z
1
2
(11)
Damit sich Symmetrie des Trägheitsellipsoids auch äußerlich zeigt, also Figurenachse existiert.
Damit Gesetzmäßigkeiten gut erkennbar sind.
62
Mechanik – Rotation II
−
Nunmehr lassen wir für eine bestimmte Zeit ∆t ein zusätzliches Drehmoment
r
M x wirken (= Momentenstoß):
r
r
r
M x ∆t = L x = J ⊥ FA ⋅ ω x
(12)
Durch den Stoß wird der Drehimpuls des
r
Kreisels um L x verändert und beträgt
nunmehr:
r r
r
r
r
L = L z + L x = J || FA ⋅ ω z + J ⊥ FA ⋅ ω x = const.
(13)
r
r
Dieser neue Gesamtimpuls L bleibt nunmehr erhalten. ω bleibt nicht erhalten,
r
r
r r
r
weder ω x , noch ω z , noch ω = ω x + ω z !
−
Wir betrachten Erot (lt. Gl. (5))
E rot =
r 1r r 1
1r
ω ⋅ J ⋅ ω = ω ⋅ L = ω|| L ⋅ L = const.
2
2
2
(14)
r r
⇒ Die Komponente von ω || L (≡ ω|| L )
ist konstant, die ⊥ dazu rotiert:
−
r
r
Beachte: ω ist das „Gesamt- ω “ (momentane Drehachse)
−
Was ins Auge springt, sind zwei andere Dinge: Die Rotation um die Figurenachr
se und deren Umlauf um die L -Achse (≡ Nutation).
−
r r
Es lässt sich zeigen, dass beim symmetrischen Kreisel ω , L und Figurenachse
in einer Ebene liegen:
63
Mechanik – Rotation II
−
Präzession: Nunmehr setzen wir den Kreisel einem ständigen Drehmoment
aus, am einfachsten durch Lagerung entfernt vom Schwerpunkt:
r
r
dL
Ma =
dt
!
(5 - 3)
r
r
r
r
r
⇒ M a = R × m ⋅ g bewirkt also Rotation von L um Achse || g (senkrechte Achse).
−
Betrag von ωp (Präzessionsbewegung):
dϕ dL 1
=
⋅
dt
dt L
ωp ... Präzessionsfrequenz
ωp =
(15)
mit (5 - 3) ist:
r
r
dL dL
=
= Ma
dt
dt
⇒
ωp =
Ma
L
Präzessionsfrequenz bei gegebenem Kreisel (d.h. Ma = const) ~
also: schnelle Rotation → kleine ωp, usw.
(16)
1
;
L
Beispiele:
n
r
(1) L = const ⇒ Stabilität beim Diskus- bzw. Speerwerfen.
(2) „ansatzweise“ Präzession beim freihändigen Radfahren: Kippen nach rechts führt
automatisch zum Lenken nach links (vgl. Abbildung oben).
(3) atomare Kreisel: magnetische Momente ∧ äußeres Magnetfeld ⇒ Präzessionsbewegung
64
Mechanik – Deformierbare Festkörper
11.
Deformierbare Festkörper
→ „Segen der Verformung“ (kippelnder Stuhl, usw.)
11.1.
Dehnung und Kompression
−
Hier steht die Kraft ⊥ auf der Bezugsfläche!
−
In Experimenten zeigt sich:
1 l⋅F
⋅
E A
E ... Elastizitätsmodul (materialspezifisch)
∆l =
mit:
Umformung ergibt:
∆l 1 F
= ⋅
l
E A
ε ... Dehnung
ε≡
mit:
Mit
(1)
F
Kraft
=
= σ ... (Normal-)Spannung
A Fläche
folgt schließlich:
ε=
1
⋅ σ bzw. ε ⋅ E = σ
E
Also: Dehnung ~ Spannung; HOOKEsches Gesetz (gilt innerhalb bestimmter
Grenzen)
Betrachtungsweisen:
!
⋅ bestimmtes aufgeprägtes σ induziert ε
⋅ bestimmtes aufgeprägtes ε induziert (inneres) σ
Maßein- [E] = N ≡ Pa ... Pascal
heit:
m2
⇒
(2)
SI
E hat Dimension einer Spannung, also Kraft/Fläche
65
Mechanik – Deformierbare Festkörper
Konvention: Zug →
Druck →
−
σ > 0, ε > 0
σ < 0, ε < 0
der gezogene/gestauchte Körper versucht, sein Volumen konstant zu halten
⇒ Querverformung / „Querkontraktion“: b → b - ∆b
!
POISSON[sche Querkontraktions]zahl µ
µ≡
−
∆b
b
∆l
l
(3)
Es zeigt sich, dass
∆V σ
= (1 − 2µ)
V
E
(4)
u
Diskussion
Für Zugspannungen (σ > 0) ist ∆V ≥ 0 ⇒ µ ≤ 0,5
Extrema: µ = 0,5 ⇒
µ=0
⇒
∆V = 0
(keine Volumenänderung; ∆l wird voll
durch ∆b ausgeglichen)
∆V maximal (keine Querverformung)
reale FK haben häufig µ = 0,2 ... 0,3
−
allseitiger Druck ∆p ⇒ jede der drei Dimensionen trägt
∆V
lt. Gl. (4) bei!
V
∆V
3 ⋅ ∆p
=
(1 − 2µ)
V
E
Erläuterung:
Schreibweise ∆p (nicht p) deshalb, weil in der
Praxis der hydrostatische Druck in der Regel
zum stets vorhandenen Luftdruck hinzukommt.
Vorzeichenkonvention: „Druck nach innen“ = p > 0 (anders als bei σ!):
∆V
3 ⋅ ∆p
=−
(1 − 2µ)
V
E
mit:
∆V
∆p
=−
V
K
E
K≡
... Kompressionsmodul
3(1 − 2µ)
∆V
hängt also von E und µ ab!
V
(5)
(6)
!
66
Mechanik – Deformierbare Festkörper
11.2.
Scherung
−
Im Gegensatz zu <11.1.> liegt hier der
Kraftvektor in der Bezugsfläche!
−
Ansonsten gilt völlig analog zu Gl. (1):
1 l⋅F
⋅
G A
G ... Schermodul (materialspezifisch)
∆l =
mit:
(7)
Mit
F
= τ ... Scherspannung
A
folgt schließlich:
−
−
⇒
∆l 1
= ⋅τ
l
G
⇒
α=
1
⋅ τ bzw. G ⋅ α = τ
G
α ... Scherwinkel
Kommentar:
Der Schwerwinkel α beschreibt die spezifische Veformung bei der Scherdeformation und tritt an die Stelle der Dehnung ε in <11.1.>.
(8)
u
!
Es lässt sich zeigen, dass auch zwischen G und E eine Beziehung besteht (analog Gl. (6)):
G≡
−
∆l
= tan α ≈ α (für kleine α)
l
E
2(1 + µ)
Kommentar:
·
·
(9)
u
Von den vier Konstanten E, G, K, µ sind nur jeweils zwei unabhängig (vgl.
die Gl. (6), (9) und analoge Zusammenhänge).
Wir haben hier Spezialfälle betrachtet! Im allgemeinen Fall gilt:
τ, σ
→
Spannungstensor
ε, α
→
Verzerrungstensor
µ, E, K, G →
Elastizitätstensor
67
Mechanik – Deformierbare Festkörper
−
Wichtige Anwendung der Scherung: Drillung (vgl. <9.4.>)
ϕ ... Torsionswinkel
Der Scherungwinkel α für ein
bestimmtes Volumenelement des
Materials nimmt mit r zu!
Für kleine α gilt:
α = r⋅
ϕ
L
(10)
Wir betrachten einen dünnen Hohlzylinder:
Seine Verdrillung liefert ein Rückstellmoment1
dM = r ⋅ dF
(11)
r
Die Kraft dF = dF wird durch die Scherspannung τ aufgebracht. Es gilt:
τ=
dF
= G ⋅α
dA
(8)
mit dA = 2πr ⋅ dr sowie Gl. (10) folgt für dF:
dF = G ⋅ r ⋅
ϕ
⋅ 2πr ⋅ dr
L
(12)
Damit erhalten wir für das Rückstellmoment dM(r) des Hohlzylinders mit dem
Radius r:
dM (r ) =
1
2π ⋅ G ⋅ ϕ 3
r ⋅ dr
L
(13)
Wir rechnen jetzt mit Beträgen!
68
Mechanik – Deformierbare Festkörper
Wenn wir alle Teil-Hohlzylinder aufintegrieren, folgt:
R
M = ∫ dM (r ) =
0
mit:
π
R4
⋅G ⋅
⋅ ϕ ≡ D* ⋅ ϕ
2
L
(14)
R ... Radius des Vollzylinders
D* ist das Richtmoment lt. Gl. (9 - 12)!
r
In <9.> hatten wir nur gesagt, dass M = D * ⋅ ϕ .
Jetzt wissen wir, wie D* von Geometrie (R, L) und Material (G) abhängt!
11.3.
Der gebogene Balken
Der Krümmungsradius R
ändert sich längs des Balkens,
wir betrachten ein kurzes
Stück, für das R ≈ const. ist.
Wir nehmen an, dass die neutrale Faser in der Mitte liegt,
dort sei z = 0.
∆l(z) = l(z) − l 0 = l 0 ⋅
−
Es gilt
l( z ) z + R
=
l0
R
⇒
l( z ) = l 0 ⋅
z+R
R
z
R
(15)
In einer Faser im Abstand z von der neutralen Faser baut sich also die folgende
Spannung auf:
σ( z ) = E ⋅ ε = E ⋅
∆l(z)
l0
Mit (15) folgt:
σ( z ) = E ⋅
z
R
(16)
69
Mechanik – Deformierbare Festkörper
Kommentar:
Oberhalb der neutralen Faser herrscht Zugspannung, unterhalb Druckspannung,
vergleiche Vorzeichenkonvention in <11.1.>, die auch hier gilt.
−
u
Blick auf einen Balkenquerschnitt:
Das Flächenelement dA = dz ž dy erfährt
eine Kraft
dF = σ(z) ⋅ dA
Mit (16) erhält man:
dF = E ⋅
z
dz ⋅ dy
R
(17)
Diese Kraft bewirkt ein Drehmoment:
dM = z ⋅ dF
dM =
E 2
⋅ z dz ⋅ dy
R
(18)
Das gesamte in der Querschnittsfläche wirkende Drehmoment folgt als:
M =
E
2
⋅
∫∫ z dz'⋅dy'
R gesamte
Quer −
schnittsfläche
I
mit:
=
∫∫ z
2
dz'⋅dy'
gesamte Quer −
schnittsfläche
I heißt Flächenträgheitsmoment.
Es gilt:
M =
E
E
⋅ I bzw. R = ⋅ I
R
M














Kommentar:
·
Ein äußeres Drehmoment biegt den Balken; andererseits wird durch eine
von außen aufgeprägte Biegung ein inneres (entgegengerichtes) Drehmoment induziert.
·
I ist formal analog zum Trägheitsmoment bei der Rotation. Es beschreibt
die Steifigkeit des Balkens (Beispiel: Doppel-T-Träger!)
(19)
u
70
Mechanik – Deformierbare Festkörper
·
Gl. (19) zeigt: großes M und/oder kleines I (= kleine Biegesteifigkeit) bewirken kleines R, d.h. große Biegung.
·
Das Gleichgewicht des durchgebogenen Balkens ist wieder gekennzeichnet durch:
∗ Kräftegleichgewicht
und ∗ Drehmomentengleichgewicht
11.4.
−
r
r
 Wenn nicht Fges = 0 und M ges = 0 wären,

 würde Translation oder Rotation bewirkt.
Inelastisches Verhalten
Beispiel für ein reales Spannungs-Dehnungs-Diagramm (dennoch schematisch):
σP ... Proportionalitätsgrenze (HOOKE)
σE ... Elastizitätsgrenze
σF ... Festigkeitsgrenze
Kommentar:
·
für σP < σ < σE keine Linearität mehr, aber noch keine bleibenden Verformungen (gegebenenfalls dauert es eine Weile, bis alles zurückgeht)
·
für σ > σE bleibende Verformungen, die bei Entlastung nicht mehr vollständig zurückgehen
·
Die ε-Werte in der Abbildung sind typisch für viele Metalle.
−
u
elastische Nachwirkung / elastische Hysterese:
71
Mechanik – Deformierbare Festkörper
Kommentar:
·
0A reiche schon in den inelastischen Bereich.
·
B ... Restverformung trotz σ = 0
·
C ... notwendige „Gegenspannung“, um ε = 0 zu erreichen
·
Fläche innerhalb der Kurve repräsentiert die bei einem Umlauf durch die
Verformung verbrauchte (= in Wärmeenergie umgewandelte) Energie W:
dW = F ⋅ dx
⇒
dW = A ⋅ σ ⋅ l ⋅ dε
u
F = σ⋅A
 ∆l 
dx = d (∆l) = l ⋅ d  = l ⋅ dε
 l 
dW = Vol. ⋅ σ ⋅ dε
−
Zeiteffekte
⋅
„richtige Festkörper“ sind Einkristalle. Sie haben definierte Grenzen für die
Verformung, ∃/ Zeiteinfluss.
⋅
Viele feste Körper sind ungeordnet (amorph). Bei ihnen hängt die Verformung auch von der Zeitdauer der Einwirkung der Spannung ab:
⇒ kurze Einwirkung: elastisches bzw. sprödes Verhalten
lange Einwirkung: plastisches Verhalten
72
Mechanik – Flüssigkeiten
12.
Flüssigkeiten
In diesem Kapitel werden ruhende Flüssigkeiten behandelt (sogenannte Hydrostatik).
12.1.
−
Einleitung
Wir reden über „richtige“ Flüssigkeiten, keine „amorphen Festkörper“!
⇒ Atome sind frei gegeneinander verschiebbar, an der Oberfläche einer Flüssigkeit können keine Tangentialkräfte auftreten.
Eine freie Flüssigkeits-Oberfläche stellt sich senkrecht zur Resultierenden aller
Kräfte ein.
!
Beispiel: beschleunigt bewegter Trog
n
M. a. W.: Der Schubmodul einer idealen Flüssigkeit ist gleich Null.
!
Beispiel:
n
Gestalt von Flüssigkeitsoberflächen bei Rotation
tan α =
2
∆m
/ ⋅ ω x dz
=
∆m
dx
/ ⋅g
dz
... Steigung der OF-Kurve
dx
Kurve ist eine Parabel!
ω2 2
⇒
z=
⋅x
2g
12.2.
Statischer Druck
⇒ Druck in der Flüssigkeit: p =
Maßeinheit:
1
F
A
N
= 1 Pa = 10-5 bar1
2
m
(1)
SI
zum Vergleich: 1 atm = 1013 mbar = 760 Torr
73
Mechanik – Flüssigkeiten
−
Der Druck in einer Flüssigkeit ist allseitig, d.h. wirkt in alle Richtungen gleich.
−
Kompressibilität: in völliger Analogie zu Gl. (11 - 6) bildet man
1
1 dV
=− ⋅
K
V dp
κ ... Kompressibilität
K ... Kompressionsmodul
κ≡
(2)
Es zeigt sich, dass für fast alle Flüssigkeiten κ so klein bzw. K so groß ist, dass faktisch keine Komprimierbarkeit besteht. „Flüssigkeiten sind praktisch volumenstabil.“
−
!
!
hydraulische Presse, Heber, o.ä.:
Felsbrocken mit Masse M
⇒
⇒
p=
F1 = M ⋅ g
F1 M ⋅ g
=
A1
A1
wegen Allseitigkeit des Druckes muss nun auch gelten
⇒
p=
m⋅g
A2
m=
A2
⋅M
A1
n
Beispiel
1000 kg (Felsbrocken) ∧ A2/A1 = 1/1000 ⇒ Masse m = 1 kg hält die Waage!
−
Ist der Energiesatz verletzt?
Wir erhöhen m um ein sehr kleines ∆m, so dass sich der kleine Kolben um ∆h2
nach unten senkt.
⇒ geleistete Arbeit:
mit:
Win = ∆h 2 ⋅ F2
Win = ∆h 2 ⋅ A 2 ⋅ p
F2 = p ⋅ A 2
(1)
∆h 2 ⋅ A 2 = V ... Flüssigkeitsvolumen
74
Mechanik – Flüssigkeiten
Das Flüssigkeitsvolumen V strömt in den dicken Kolben und hebt diesen um ∆h1
gegen die Kraft F1:
⇒ am Fels geleistete Arbeit:
Wout = ∆h 1 ⋅ F1
F1 = p ⋅ A1
(1)
Wout = ∆h 1 ⋅ A1 ⋅ p
Wobei wiederum
⇒
12.3.
−
∆h 1 ⋅ A1 = V ist.
Weil V in beiden Fällen gleich ist und p sowieso konstant, ist Win = Wout.
Hydraulik spart Kraft und braucht mehr Weg → Goldene Regel der Mechanik. Die Energie bleibt erhalten.
Schweredruck
Wir haben bis jetzt außer Acht gelassen, dass sich in einer Flüssigkeit ein
Schweredruck aufbaut:
Gewicht einer Flüssigkeitssäule (Querschnitt A, Höhe h, Dichte ρ)
FG = A ⋅ h ⋅ ρ ⋅ g
(3)
⇒ Schweredruck p(h):
p( h ) =
−
FG
= h ⋅ρ⋅g
A
(4)
Schweredruck nimmt mit der Tiefe zu und hängt nur von der Tiefe ab, sofern ρ
druckunabhängig ist, d.h. Inkompressibilität besteht.
Beispiel: Wasser ( ρ ≈ 10 3
kg
)
m3
n
1
≈ 5 ⋅ 10 −10 Pa −1
K
⇒ In 10.000 m Tiefe (bei 1000 atm) ist Dichte nur um 5% erhöht!
⇒ 1 bar ≈ 1 atm pro 10 m Tiefe, Kompressibilität κ =
−
Schweredruck und statischer Druck wirken zusammen. Oft ist einer der beiden
vernachlässigbar:
!
⋅ Meer (s.o.) ⇒ statischer Luftdruck vernachlässigbar
⋅ Hydraulikanlage ⇒ Schweredruck vernachlässigbar
−
hydrostatisches Paradoxon: „Der Bodendruck ist unabhängig von der Form des
Gefäßes.“ (nur abhängig von der Höhe!)
!
75
Mechanik – Flüssigkeiten
Alle diese Gefäße haben
gleichen Bodendruck!
Wenn wir die Gefäße unten verbinden (z.B. ein bereits gefülltes Verbindungsstück anfügen), wird sich wegen des einheitlichen Drucks in Bodennähe nichts ändern.
⇒ kommunizierende Gefäße haben gleiches Flüssigkeitsniveau!
n
Beispiele:
⋅ Wasserstandsanzeiger:
⋅ Schlauchwaage
12.4.
−
Auftrieb und Schwimmen
quaderförmiger Körper in einer Flüssigkeit, Höhe H, Grundfläche A:
Schweredruck der Flüssigkeit in der Tiefe h beträgt:
p = h ⋅ ρ Fl ⋅ g
⇒
auf obere Fläche wirkt Kraft
auf untere Fläche wirkt
(5)
F1 = h 1 ⋅ ρ Fl ⋅ g ⋅ A nach unten
F2 = h 2 ⋅ ρ Fl ⋅ g ⋅ A nach oben
In der Summe erfährt der Körper die Auftriebskraft FA
= Volumen V! (h1 - h2 = H)
á
64748
FA = F2 − F1 = ρ Fl ⋅ g ⋅ A ⋅ (h 2 − h 1 )
FA = g ⋅ ρ Fl ⋅ V
Die Auftriebskraft entspricht dem Gewicht der verdrängten Flüssigkeitsmenge.
−
(6)
!
Die o.g. Herleitung ist zwar vereinfacht, Gl. (6) gilt aber für beliebig geformte Körper.
76
Mechanik – Flüssigkeiten
−
r
r
Das Verhalten des Körpers wird von FA + FG bestimmt:
!
r
r
FA < FG ⇒ Sinken; Körper ist schwerer
r
r
FA = FG ⇒ Körper schwebt
r
r
FA > FG ⇒ Körper schwimmt,
r
r
d.h. er taucht nur soweit ein, wie nötig ist, damit FA = FG ist:
Also:
Gewicht der verdrängten Wassermenge
= Gesamtgewicht des Schiffes
−
Stabilität:
Schwerpunkt S des Schiffes = Angriffspunkt der Schwerkraft
Schwerpunkt SF der verdrängten Flüssigkeit = Angriffspunkt der Auftriebskraft
⇒
12.5.
völlige Kentersicherheit nur, wenn S tiefer liegt als SF (schwerer Kiel); ansonsten existieren unterschiedliche kritische Kippwinkel
Oberflächenspannung
−
Experimente zeigen: Flüssigkeiten sind bestrebt, ihre Oberfläche klein zu halten
−
Deutung: ∃ gegenseitige Anziehung der Moleküle
der Flüssigkeit, wodurch diese zusammengehalten wird.
Moleküle an der Oberfläche erfahren resultierende
Kraft in die Flüssigkeit hinein → „Gummihaut“
2 Seiten einer Sache!
á
â
−
Energiedeutung: Ausbildung einer chemischen Bindung bedeutet Energieminimierung (Bindungsenergie wird frei!). Moleküle an der Oberfläche sind unvollständig
abgebunden ⇒ Oberfläche ist energetisch benachteiligt (∃ zusätzliche Wob)
⇒ Streben nach Minimierung der Oberfläche
−
Oberflächenenergie Wob ist proportional zur Oberfläche:
Wob = σ ⋅ A
Wob
A
σ ... spezifische Oberflächenenergie
σ
=





(7)
77
Mechanik – Flüssigkeiten
−
Maßein- [σ] = J (Energie pro Fläche)
heit:
m2
SI
Die spezifische Oberflächenenergie heißt auch Oberflächenspannung.
!
Experiment: Aufspannen eines Flüssigkeitshäutchens mittels Drahtbügel:
Die mechanische Arbeit
∆W = F ⋅ ds
(8)
vergrößert die Oberflächenenergie um
∆Wob = σ ⋅ ∆A
∆A = 2 ⋅ b ⋅ ds
â
2 Oberflächen!
∆Wob = σ ⋅ 2 ⋅ b ⋅ ds
(9)
Gleichsetzung von (8), (9)
⇒
⇒
F ⋅ ds = σ ⋅ 2 ⋅ b ⋅ ds
F
σ
=
2b
(10)
Wir können σ also auch als Zugkraft pro Länge (in der Oberfläche), also als sogenannte Linienspannung auffassen:
Maßeinheit: [σ] =
−
N N⋅m
=
... (Kraft/Länge)
m
m2
J
= 2 ... (Energie/Fläche), also identisch zu Gl. (6)!
m
SI
Der Innendruck in einer Seifenblase:
Eine Verkleinerung des Radius um dr reduziert die Oberfläche OF einer Seifenblase um
dOF
⋅ dr
dr
dOF = 8πr dr
dOF =
(
)
d 4πr 2
= 8πr
dr
(11)
Die Seifenblase hat eine äußere und eine innere Oberfläche, daher ergibt das
dOF lt. Gl. (11) eine Reduzierung der Oberflächenenergie um
dWob = 16πr dr ⋅ σ
(12)
78
Mechanik – Flüssigkeiten
Bei r-Reduzierung muss aber gegen den Innendruck mechanische Arbeit geleistet werden:
dW = F ⋅ dr
F = Kugeloberfläche ⋅
â
4πr 2
Kraft
Kugeloberfläche
â
p
dW = 4πr 2 ⋅ p ⋅ dr
(13)
Im Gleichgewicht haben sich r und p so eingestellt, dass dW = dWob ist.
⇒ Gleichsetzung von (12) und (13) liefert
p=
4σ
r
(14)
u
Kommentar:
·
·
·
p ist der in der Blase gegenüber der Umgebung herrschende Überdruck
p wächst mit zunehmendem σ und abnehmendem r!
Entsprechend Gl. (14) herrscht auch in jeder einfachen, nach außen mit Radius r gekrümmten Oberfläche ein Druck:
p=
12.6.
2σ
r
(15)
Fest-flüssig-Grenzflächen
12.6.1. Benetzung
−
Wir betrachten jetzt 3 Phasen:
·
·
·
Festkörper,
Flüssigkeit,
Gasphase (Luft + Dampf der Flüssigkeit + Dampf des Festkörpers).
Einstellen des Gleichgewichts an einer senkrechten Wand in einer Flüssigkeit bedeutet
Einstellung eines Randwinkels θ so, dass
σ ffl + σ fld ⋅ cos θ = σ fd
(16)
(YOUNGsche Gleichung)
−
Der gezeichnete Fall ist der der Benetzung (θ < 90° ≡ σfd > σffl)
79
Mechanik – Flüssigkeiten
−
andere Möglichkeit: Nichtbenetzung
(θ > 90° ≡ σfd < σffl)
−
Wenn nun selbst θ = 0 nicht reicht, um σfd zu kompensieren, gilt
σ fd > σ fld + σ ffl
Dann findet vollständige Benetzung statt, d. h. die Flüssigkeit kriecht als sehr
dünne Schicht ganz die Wand hoch; θ = 0°; σfd ist unendlich groß.
−
ähnlich beim Tropfen auf einer Oberfläche:
−
Benetzung ist wichtig!
·
·
·
·
Waschmittel (Reinigungswirkung)
Spülmittel („ohne abzutrockenen“)
Gefieder der Wasservögel
selbstreinigende Oberflächen






Benetzung
Nichtbenetzung
12.6.2. Kapillarität
−
In sehr dünnen Röhren steigen Flüssigkeiten höher als in ihrer Umgebung.
!
Zur Deutung nehmen wir vereinfachend
an, dass vollständige Benetzung vorliegt,
d.h. θ = 0° ist. (Ansonsten tritt dieser Effekt auch auf, aber nicht so ausgeprägt.)
−
verschiedene Deutungen möglich (mehrere Seiten derselben Medaille):
a) Die zusätzliche Flüssigkeitssäule mit
FG = πr 2 h ⋅ ρ ⋅ g
hängt an ihrer Randlinie (Länge 2πr) mit der Linienspannung σ fest.
⇒ Infolge dieser Spannung tritt eine „Haltekraft“ F auf:
F = 2πr ⋅ σ
80
Mechanik – Flüssigkeiten
Die Haltekraft kompensiert das Gewicht der zusätzlichen Flüssigkeitssäule:
πr 2 hρg = 2πrσ
2σ
h =
rρg
(17)
Also: Effekt umso größer, je größer σ ist und je kleiner r und ρ sind.
b) Der Schweredruck der Zusatzsäule ist
ps =
Gewichtskraft πr 2 hρg
=
= hρg
Grundfläche
πr 2
Er wird kompensiert durch den negativen Druck (d.h. Zug) der hier konkav
gewölbten Oberfläche lt. Gl. (15), also
2σ
= hρ g
r
â
Gl. (15)
≡ Gl. (17)
c) Man erhält ebenfalls das gleiches Ergebnis, wenn man alle Energien betrachtet (Oberflächenenergien, Epot der Säule, usw.) und das Minimum sucht.
− Im nichtbenetzendem Fall (z.B. Glas/Hg) tritt Kapillardepression auf:
81
Mechanik – Gase
13.
Gase
13.1.
Kompressibilität
−
Experiment:
−
Ergebnis:
p ⋅ V = const. (bei konst. T)
(Gesetz von BOYLE-MARIOTTE)
bzw.
V=
(1)
const.
p
nach Ableitung folgt
dV
const
V
=− 2 =−
dp
p
p
1 dV
1
⋅
=−
V dp
p
1
= − = −κ
K
Also:
−
Kompressibilität ... κ =
|:V
(12 -2)
1 1
= (plausibel!)
K p
(2)
gegeben: Gas der Masse M im Volumen V ⇒ für Massendichte ρ gilt
ρ=
M
V
mit Gl. (1)
⇒
1
p
=
V
const.
⇒
p
const.
ρ
ρ ~ p bzw.
= const
p
⇒
ρ = M⋅
(3)
82
Mechanik – Gase
13.2.
−
Schweredruck in Gasen
vgl. <12.3.>: Schweredruck in Flüssigkeiten (dort: Inkompressibilität!)
Bei Gasen ∃ jedoch Kompressiblität ⇒ Dichte in jeder Höhe
wird von der darüber liegenden
Säule bestimmt!
⇒ Gl. (12 - 4) gilt nur noch für
Säule mit infinitesimaler Höhe dh:
dp = −ρ(h ) ⋅ g ⋅ dh 1
−
(4)
ρ
= const ist.
p
Dies gilt gilt auch für die Erdoberfläche (Index 0) bzw. jede beliebige Höhe h:
Lösung der Differentialgleichung (4): Wir wissen aus Gl. (3), dass
ρ
ρ
ρ(h )
= const = 0 =
p
p 0 p( h )
(5)
Mit Gl. (5) wissen wir nun, dass
ρ( h ) =
ρ0
⋅ p( h )
p0
dp = −
ρ0
⋅ p(h ) ⋅ g ⋅ dh
p0
ist, also
(4‘)
Gl. (4‘) umgestellt liefert:
p(h )
∫
p0
h
ρ0
dp
=−
⋅ g ⋅ ∫ dh '
p( h ' )
p0
0
 p( h ) 
ρ ⋅g
 = − 0 ⋅ h
ln
p0
 p0 
p(h ) = p 0 ⋅ e
−
ρ0
⋅g⋅h
p0
(6)
Dies ist die barometrische Höhenformel.
1
Das negative Vorzeichen gilt wegen der p-Abnahme mit h-Zunahme. - In <12.> war dies
bedeutungslos!
83
Mechanik – Gase
Kommentar:
·
Wenn wir die richtigen ρ0, p0, g einsetzen, folgt, dass p(5500 m) ≈ 0,5žp0 ist.
Außerdem führt jede weitere Verdopplung von h zu einer Halbierung von p
u
( )
p
(Potenzgesetz a np = a n !).
·
·
Innerhalb der Höhenbereiche, in dem p faktisch = 0 wird, darf g = const.
betrachtet werden.
Gl. (6) gilt für T = const.
84
Mechanik – Strömende Flüssigkeiten und Gase
14.
Strömende Flüssigkeiten und Gase
14.1.
Vorbemerkungen
−
Es gibt viele Analogien zwischen Flüssigkeiten und Gasen (wegen der freien
Verschiebbarkeit der Teilchen); Hauptunterschied liegt in der Kompressibilität
jedoch:
Bei v << vSchall verhalten sich auch strömende Gase praktisch inkompressibel,
d.h. es erfolgt kein Aufbau von Druckwellen.
!
⇒ Daher im folgenden Annahme eines inkompressiblen Fluids.
−
Beschreibung von Strömungen nach EULER (1707 - 1783) anhand des Ger
schwindigkeitsfeldes v( r ) .
r
Sonderfall: v( r ) = zeitlich const. ⇒ stationäre Strömung
−
stationäres Strömungsfeld beschrieben durch Stromlinien:
Stromröhre = Bündel von Stromlinien
Tangente an der Stromlinie
r
→ Richtung von v
Dichte der Stromlinien
r
→ Betrag von v
−
Die Abbildung zeigt, dass pro Zeiteinheit ∆t ein strömendes Volumenelement
∆V an jeder Stelle der Stromröhre konstant ist
& = ∆V = A ⋅ v = const. (innerhalb der Stromröhre)
V
∆t
& ... Volumenstrom
V
(1)
Gl. (1) heißt Kontinuitätsgleichung: Wenn in der Stromröhre kein Medium erzeugt oder vernichtet wird, muss I konstant bleiben und v sich entsprechend A
einstellen.
!
Kommentar:
Hier ist die Quellen- und Senkenfreiheit eigentlich fast selbstverständlich (ein
Beispiel für eine Ausnahme wäre eine chemische Reaktion im strömenden Gas,
die das Volumen verändert). In der Elektrodynamik ist das anders, obwohl ansonsten viele Analogien existieren!
u
85
Mechanik – Strömende Flüssigkeiten und Gase
14.2.
Innere Reibung
... in strömenden Medien
n
Beispiel: Löffel aus Honig herausziehen
⇒ Geschwindigkeitsübergang...
von v = 0 (entfernt vom Löffel)
auf v = vLöffel (an der Löffel-Oberfläche)
−
Es zeigt sich, dass für die Reibungskraft FR gilt
dv
dx
A ... Wechselwirkungsfläche
FR ~ A ⋅
mit:
dv 1
dx
η ... Viskosität, dynamische Zähigkeit
FR = η ⋅ A ⋅
mit:
FR
dv
= η⋅
A
dx
τR ... Reibungs-Schubspannung; viskose Schubspannung
τR =
Maßein- [η] = N ⋅ s
heit:
m2
(2)
(3)
SI
Gl. (2), (3) heißen NEWTONsches Gesetz der inneren Reibung.
n
Beispiele:
Substanz
Glycerin
H2O
Luft
H2
1
20°C
0°C
20°C
100°C
0°C
0°C
η in Nsm-2
1,53
0,0018
0,0010
0,0003
0,00002
0,00001
Vorzeichen in Gl. (2) stimmt, da



(typisch: Abnahme mit steigendem T!)
dv
< 0!
dx
86
Mechanik – Strömende Flüssigkeiten und Gase
−
Deutung:
Überwindung der Potentialhügel beim
Gegeneinander-Verschieben der Flüssigkeitsschichten
−
Strömungen, deren Verhalten durch die innere Reibung bestimmt ist, d.h., bei
denen sich nicht vermischende Schichten des Mediums gegeneinander verschoben werden, heißen laminare Strömungen.
14.3.
!
Beispiele für laminare Strömungen
14.3.1. Laminare Rohströmung
−
Die Flüssigkeit haftet an der Wand und
hat in der Mitte des Rohres maximale Geschwindigkeit
−
Wir betrachten nun einen Flüssigkeitszylinder um die Rohrachse:
−
An der Mantelfläche wirkt die Reibungskraft (mit Gl. (2))
FR = 2πrl ⋅ η ⋅
dv
dr
(4)
â
(= AMantel)
−
Auf seine Grund- und Deckflächen wirkt die Netto-Druckkraft
Fp = πr 2 (p1 − p 2 )
â
(= AGrund/Deck)
(5)
Fp treibt die Flüssigkeit voran und überwindet genau FR: Fp = FR.
87
Mechanik – Strömende Flüssigkeiten und Gase
⇒ aus (4), (5) erhalten wir
dv p1 − p 2
=
⋅r
dr
2η l
und nach Integration
v( r ) =
(
∆p 2
R − r2
4ηl
)
(6)
Dies ist ein parabolisches Geschwindigkeitsprofil v(r) = A - B ž r2, wie in der
Skizze schon gezeigt.
−
&
Interessant ist die Durchflussmenge V
(Volumen/Zeit) bei gegebenen ∆p, η, R.
Wir betrachten einen Hohlzylinder mit
der Dicke dr:
Der Volumenstrom im Querschnitts-Flächenelement dA ist
dV
dt
Fl.− Element
(dz ž dA = dV!)
á
dz
=
⋅ dA = v(r ) ⋅ 2πr dr
dt
Gesamt-Volumenstrom im Rohr durch Integration über alle Flächen-Elemente:
R
& = v(r ) ⋅ 2πr dr
V
∫
0
mit v(r) lt. Gl. (6) folgt
& = π ⋅ ∆p ⋅ R 4
V
8ηl
(7)
Dies ist das HAGEN-POISEUILLEsche Gesetz.
u
Kommentar:
Radius geht mit 4. Potenz ein!


Gl. (7) stellt das „OHMsche

Gesetz für die laminare Roh- 

strömung“ dar:

I =
& =
V
U
R
Triebkraft
∆p
=
(Strömungs −)Widerstand  8ηl 


 πR 4 
88
Mechanik – Strömende Flüssigkeiten und Gase
14.3.2. Laminares Umströmen einer Kugel
−
An diesem Beispiel soll eine in der Strömungsmechanik häufig verwendete, sehr
nützliche Betrachtungsweise erläutert werden: die Unterteilung in einen Nahbereich,
in dem das Fluid anhaftet, und den unbeeinflussten Außenbereich der Strömung.
−
Experiment: Wir ziehen eine Kugel mit der Geschwindigkeit v durch eine Flüssigkeit.
·
Nahe Kugel-Oberfläche ist Strömungsgeschwindigkeit = v
(Anhaften der Flüssigkeit)
·
In einiger Entfernung von der Kugel
ruht die Flüssigkeit („merkt nichts“)1
dv v
≈ ; Wechselwirkungs-Fläche A = Kugel-OF = 4πr2
dr r
⇒
Damit ergibt sich für Gl. (2)
dv
v
= η ⋅ 4πr 2 ⋅
dx
r
FR = −4πrηv
FR = η ⋅ A ⋅
Die ungleich schwierigere korrekte Herleitung lieferte
FR = −6πrηv
14.4.
(3 - 19)
Turbulente Strömungen, Ähnlichkeit, Strömungsgrenzschicht
−
Experiment zeigt: Bei bestimmter Geschwindigkeit bricht laminare Strömung
zusammen: Wirbelbildung; Nichtlinearität, chaotisches Verhalten = Turbulenz
−
Es zeigt sich, dass vkrit in Abhängigkeit von
·
ρ
... Dichte
·
η
... Viskosität
·
l
... Abmessung (z.B. Kugel-Durchmesser)
!
unterschiedliche Werte annehmen kann
−
also: entscheidend ist nicht v, sondern eine Größe Re
ρ⋅v⋅l
η
Re... REYNOLDsche Zahl
Re ≡
!
(8)
1
Die hier betrachete "r-Umgebung" ist nicht identisch mit der Grenzschichtdicke in <14.4>.
89
Mechanik – Strömende Flüssigkeiten und Gase
l ist eine typische Abmessung des strömenden Systems.
Re ist dimensionslos:
Maßeinheit:
[Re] =
kg m m m ⋅ s
⋅ ⋅ ⋅
=1
m 3 s 1 kg
SI
Re hat die physikalische Bedeutung des Quotienten aus kinetischer Energie und
Reibungsenergie.
−
Bei einem bestimmten Re schlägt die Strömung um. Der Übergang ist jedoch
nicht scharf, sondern ein Bereich (z.B. Re = 1000 - 2000)1
!
Gründe:
·
Einfluss der Oberflächen-Rauheit, u.ä.
·
Strömung kann „instabil-laminar“ sein (gewisse Analogie zur unterkühlten
Flüssigkeit)
−
Strömungen mit gleicher Re sind ähnlich → Modellierung im Wind- oder
Strömungskanal
!
kleines l (Schiffsmodell) ⇒ Anpassung von v sowie gegebenenfalls ρ, η damit
gleiches Re herauskommt.
−
Strömungsgrenzschicht: Fluid haftet an umströmten Oberflächen (Kugel,
Rohrwandung), d.h. v = 0, und gleicht sich dann allmählich an die in einiger
Entfernung herrschende „ungestörte Strömung“ an.
Beispiel:
⋅
Fluid an einer Wand
⋅
Herausziehen einer Platte aus
ruhendem Fluid
n
Die beiden dargestellten Fälle sind völlig analog!
1
Deswegen ist die Frage „Was ist die typische Länge bei einer bestimmten unregelmäßigen
Form?“ auch nicht so kritisch!
90
Mechanik – Strömende Flüssigkeiten und Gase
−
Übergangsbereich wird durch Grenzschicht definierter Dicke D mit linearem
Geschwindigkeitsübergang angenähert (s. Abbildung zur bewegten Platte):
x

v ( x ) = v 0 ⋅ 1 − 
 D
=0
für x < D
für x ≥ D





(9)
Mit Gl. (9) vereinfacht sich das NEWTONsche Reibungsgesetz (Gl. (2)) zu
v0
D
â
dv
(= )
dx
FR = −η ⋅ A ⋅
(10)
Um die Platte herauszuziehen, muss stetig eine Kraft F = - FR aufgewandt werden. Diese führt lt. Gl. (3 - 6) zu einem Impulsübertrag an das Fluid:
F=
dp
dt
(3 - 6)
⇒ Wenn F = - FR die Zeit ∆t lang wirkt, wird übertragen:
( v 0 ⋅ ∆t = l ... herausgezogene Länge)
á
v0
∆p = F ⋅ ∆t = − FR ⋅ ∆t = +η ⋅ A ⋅
⋅ ∆t
D
(11)
∆p findet sich im Fluid wieder, das - in seinen einzelnen Schichten
unterschiedlich – beschleunigt wurde: Aufintegration des im Fluid
steckenden Impulses:
D
∆p = ∫ v( x ) ⋅ dm
dm = ρ ⋅ dV = ρ ⋅ A ⋅ dx
0
D
∆p = ρ ⋅ A ⋅ ∫ v( x ) dx
0
x

v ( x ) = v 0 ⋅ 1 − 
 D
lt. Gl. (9)
D
x

∆p = ρ ⋅ A ⋅ v 0 ⋅ ∫ 1 −  dx
D
0
D
∆p = ρ ⋅ A ⋅ v 0 ⋅
2
(12)
91
Mechanik – Strömende Flüssigkeiten und Gase
Wegen der Impulserhaltung müssen (11) und (12) gleich sein
⇒
mit
l
D
= ρ ⋅ A ⋅ v0 ⋅
D
2
2ηl
D=
ρv 0
η⋅ A ⋅
(13)
D ist die Dicke der (PRANDTLschen) Strömungsgrenzschicht.
u
Kommentar:
·
·
·
Gl. (13) ist eine Näherung, gibt die Tendenz der Abhängigkeit von η, l, ρ, v0.
l hat die Bedeutung einer charakteristischen Länge.
Die Annahme, dass v(x) linear ist, gilt natürlich besonders für D << l, wenn
„das Fluid nur eine große ebene Wand sieht“:
D=
2ηl
<< l
ρv 0
2η l
<< l 2
ρv 0
ρv 0 l
2 <<
= Re
η
|[
]2
|⋅
ρv 0
η
≡ (8)
Also: Die Näherung des linearen v(x)-Verlaufs gilt für große Re, wo unter Umständen bereits Turbulenz auftritt.
−
Bedeutung der Strömungsgrenzschicht
a)
als Modell:
b) physikalisch: Durch das „Anhaften“ der Strömung wird der Transport beeinflusst: Feuchtigkeit, Wärme usw. müssen durch D hindurch diffundieren; die Möglichkeiten des zwangsweisen Anoder Abtransports enden am Grenzschichtrand.
Jedoch: großes v0 ⇒ kleines D ⇒ Transport erleichtert!
14.5.
−
Reibungsfreies Fluid: BERNOULLIsche Gleichung
Wir betrachten jetzt ein reibungsfreies Fluid, d. h. eine existierende Druckdifferenz (p1 ≠ p2 ) wird nicht zur Aufrechterhaltung der Strömung benötigt.
92
Mechanik – Strömende Flüssigkeiten und Gase
−
Das Rohr weise eine Verengung auf:
Wegen der Gültigkeit der Kontinuitätsgleichung (Gl. (1)) ist
& = ∆V = A ⋅ v = A ⋅ v = const.
V
1
1
2
2
∆t
(1‘)
⇒ Im Beispiel lt. Abbildung nimmt v zu!
Ebenfalls verändert sich an der Verengung der Druck von p1 auf p2:
Druckarbeit links:
∆W1 = p1A1 ⋅ ∆x 1 = p1 ⋅ ∆V
â
(= F1)
Druckarbeit rechts:
∆W2 = p 2 A 2 ⋅ ∆x 2 = p 2 ⋅ ∆V
â
(= F2)
∆W1 wird zum Teil verwendet, den Druck p2 zu überwinden, also W2 zu leisten.
Der Rest (= ∆W1 - ∆W2) wird zur Beschleunigung des Fluids aufgewendet:
∆W1 − ∆W2 = (p1 − p 2 ) ⋅ ∆V =
1
⋅ ρ ⋅ ∆V ⋅ ( v 22 − v12 )
2
â
(= ∆m)
(14)
nach Umstellung folgt
p1 +
ρ 2
ρ
v1 = p1 + v 22
2
2
verallgemeinert
p+
ρ 2
v = p ges = const.
2
(15)
Dies ist die BERNOULLIsche Gleichung.
93
Mechanik – Strömende Flüssigkeiten und Gase
ρ 2
v hat die Dimension eines Druckes1 und heißt Staudruck. p heißt statischer Druck.
2
u
Kommentar:
·
·
−
Für v = 0 ist p = pges, der (maximale) statische Druck. Mit zunehmendem v
sinkt p.
Bei p = 0 („druckloser Ausfluss“) wird der Staudruck maximal. Wird v reduziert, baut sich wieder zunehmender p auf.
Bisher betrachtet: Waagerechte Strömung, d.h. potentielle Energie im Erdschwerefeld war konstant. Wenn wir unterschiedliche Höhen
einbeziehen wollen, müssen wir noch den Schweredruck2
ρžgžh berücksichtigen und erhalten:
p+
ρ 2
v + ρ ⋅ g ⋅ h = p ges = const.
2
(16)
Dies ist die verallgemeinerte BERNOULLIsche Gleichung.
−
Die BERNOULLIsche Gleichung ist der Energiesatz (bezogen auf das Volumen)
für das Fluid. Diesbezügliche Bedeutung der einzelnen Glieder:
E pot
m
⋅g⋅h =
V
V
m
E
ρ 2
v = V v 2 = kin
2
2
V
A⋅x
Druckarbeit
p=
⋅p
=
V
V
ρgh =
−
(Staudruck)
(statischer Druck)





·
hydrodynamisches Paradoxon
Bunsenbrenner
Wasserstrahlpumpe
Zerstäuber
·
Kavitation: Wir betrachten Gl. (15) und formen um
·
·
⇒
2
(Schweredruck)
Beispiele zur BERNOULLIschen Gleichung
·
1
!
v=
2p ges
v>
2p ges
ρ
ρ
"v ↑ ⇒ p ↓"
entspricht p = 0
entspricht einem statischen Druck p < 0!
kg m 2
m 1
N
Kraft
⋅ 2 = kg ⋅ 2 ⋅ 2 = 2 →
!
2
m s
s m
m
Fläche
kg m
m 1
N
Kraft
Dimension von ρ ⋅ g ⋅ h : 3 ⋅ 2 = kg ⋅ 2 ⋅ 2 = 2 →
!
m s
s m
m
Fläche
94
Mechanik – Strömende Flüssigkeiten und Gase
Dies unter Umständen leicht erreicht, z.B. bei H2O für v ≥ 14m ž s-1
⇒ Bildung von Dampf-/Gasbläschen (z.B. verdampfte Flüssigkeit)
die bei Reduzierung von v implosionsartig zusammenbrechen
⇒ Druckwellen → Materialzerstörung (Kavitation)
·
Dynamischer Auftrieb:
Infolge der Anfahrtswirbel entsteht Tragflächenumströmung:
vo > vu ⇒ po < pu ⇒ Auftrieb
14.6.
−
Strömungswiderstand
... kann über die BERNOULLIsche Gleichung verstanden werden:
a) langsame Strömung ⇒ völlig symmetrisches Bild
v-Verteilung vor und hinter der Kugel
gleich ⇒ keine resultierende Kraft
b) schnelle Strömung ⇒ Bildung von Wirbeln hinter dem Hindernis:
v hinter der Kugel erhöht (Die „unregelmäßige Richtung“ von v spielt keine
Rolle, die BERNOULLIsche Gleichung ist
eine Energieangelegenheit!)
⇒ statischer Druck p hinter der Kugel
ist reduziert
⇒ Kraft, die die Kugel mitreißen will
−
Diese „Druckwiderstandskraft“ ist dem Staudruck proportional.
(= Staudruck)
á
1 2
F = c w ⋅ ρv ⋅ A
2
A ... Querschnittsfläche
cw... Widerstandsbeiwert
Kommentar:
·
(17)
u
Wir sind wieder ein mal am Rand der Gültigkeit des Modells. Die Initiierung des Wirbelfeldes setzt natürlich Reibung voraus, wenn auch dann die
Argumentation wieder auf der BERNOULLIschen Gleichung beruht.
95
Mechanik – Strömende Flüssigkeiten und Gase
·
−
Deutung: Staudruckabhängigkeit (Staudruck korreliert mit Ekin, s.o.) deshalb, weil infolge Wirbelbildung diese Ekin der Kugel „nur von vorn, nicht
auch von hinten“ zugeführt wird ⇒ resultierende Kraft!
cw ist abhängig von der Körperform. Beispiele (Strömung von links):
1,35
!
1,12
0,40
0,056
(PKW
0,25 ... 0,50)
96
Mechanik – Schwingungen II
15.
−
Schwingungen II
vgl. hierzu auch <6.1.> Federschwinger
15.1.
2D-Überlagerung von Schwingungen
−
Wir wissen, dass die Gesetze der Mechanik für jede Dimension einzeln gelten
und sich die Bewegungen dann überlagern.
−
Beispiel: 2 Schwingungen mit ωx = ωy
·
ohne Phasenverschiebung (Kurve a):
x ( t ) = A ⋅ sin ωt
y( t ) = A ⋅ sin ωt
in x-Richtung:
in y-Richtung:
·
mit Phasenverschiebung
in y-Richtung:
−
mit beliebiger Phasenverschiebung: ⇒ alle Übergänge Linie → Ellipse → Kreis
Schwingungen nun mit ωx ≠ ωy:
ω
n
·
für rationales x = : geschlossene Kurven (LISSAJOUS-Figuren) oder in
sich zurücklaufende Linien (analog der Geraden
ωy m
(n, m natürliche Zahlen) für ωx = ωy)
·
15.2.
−
π
(Kurve b):
2
x ( t ) = A ⋅ sin (ωt + π 2)
= A ⋅ cos ωt
y( t ) = A ⋅ sin ωt
in x-Richtung:
·
n
für irrationales
ωx
:
ωy
vollständiges Überstreichen der Fläche
Schwebungen
Überlagerung zweier gleich gerichteter Schwingungen mit nahezu derselben
Frequenz:
x̂ ( t ) = x̂ 1 ( t ) + x̂ 2 ( t ) = A1 ⋅ e iωt + A 2 ⋅ e i (ω+ ε) t
iεt
x̂ ( t ) = (A1 + A 2 ⋅ e ) ⋅ e
â
Â
i ωt
!
(1)
(2)
⇒ Eine Schwingung mit Frequenz ω und einer zeitlich veränderlichen komplexen
Amplitude Â!
97
Mechanik – Schwingungen II
−
Realteil der Schwingung:
x ( t ) = Re{x̂ ( t )}
−
Beispiel: 2 Schwingungen mit gleicher Amplitude bei nahezu gleicher Frequenz
⇒
−
−
n
x 1 ( t ) = A ⋅ cos ωt
x 2 ( t ) = A ⋅ cos(ω + ε) t
x ( t ) = 2A ⋅ cos (ω + ε 2) t ⋅ cos (ε 2) t = x 1 ( t ) + x 2 ( t )
Realisierung:
15.3.
(3)
z.B. Überlagerung zweier fast gleich hoher Töne (schlecht gestimmtes Instrument)
Die FOURIER-Analyse
gegeben: Schwingung = beliebiger zeitlich periodischer Vorgang, d.h.
x ( t ) = x (t + T)
T ... Periodendauer
Die Abbildung zeigt den allgemeinen Fall. Nicht alle Schwingungen sind harmonisch!
!
!
98
Mechanik – Schwingungen II
−
FOURIER (1822): Jede zeitlich periodische Funktion mit der Periodenlänge T lässt
sich aus harmonischen Schwingungen aufbauen (FOURIER-Reihe).
2π
T
x ( t ) = x 0 + x 1 ⋅ cos (ωt + ϕ1 ) + x 2 ⋅ cos (2ωt + ϕ 2 ) + K
x ( t ) = x ( t + T ) ; ω = 2πν =
∞
x ( t ) = ∑ x n cos (nωt + ϕ n )
n =0







!
(4)
bzw. in komplexer Form:
∞
x̂ ( t ) = ∑ x̂ n e inωt
(4‘)
n =0
Beispiel:
n
Gleiche Töne bei unterschiedlichen Musikinstrumenten unterscheiden sich in ihren
Obertönen, d.h. den Gliedern der Fourierreihe mit n > 1.
99
Mechanik – Schwingungen II
15.4.
−
Gekoppelte Schwinger
z.B. gekoppelte Pendel oder gekoppelte Federschwinger (Luftkissenbahn):
Gegeben sind:
2 Federschwinger im entsprechenden Zustand + Verbindungsfeder
passender Länge, so dass alle 3 Federn gleichzeitig entspannt sind:
−
ohne Verbindungsfeder gilt z.B. für m1:
D ⋅ x1 + m ⋅
d2
x1 = 0
dt 2
(6 - 2‘)
nunmehr noch zusätzliche Federkraft, die von x2 - x1 abhängt1:
F* = ( x 1 − x 2 ) ⋅ D *
(5)
Wenn x1 = x2 ist, hat die Feder ihre Gleichgewichtslänge und übt keine Kraft aus!
⇒ Differentialgleichungen
für m1:
für m2:
d2
D ⋅ x1 + D ⋅ (x 1 − x 2 ) + m ⋅ 2 x1
dt
d2
*
D ⋅ x 2 + D ⋅ (x 2 − x1 ) + m ⋅ 2 x 2
dt
*






=0
=0
(6)
Dies ist ein System von gekoppelten Differentialgleichungen.
−
−
1
Beschreibung der Lösung: ∃ 2 Fundamentallösungen
a) beide Federn schwingen parallel, Feder wird
nicht beansprucht (wie beim Einzelpendel!):
b) beide Federn schwingen gegeneinander (diese
Schwingung ist schneller, wegen der Zusatzfeder):
ω0 =
D
m
ω0 =
D + 2D *
m
Allgemeiner Fall = Linearkombination beider Lösungen („mathematische Aussage“)
Vorzeichen: Für x2 < x1 ist x1 - x2 > 0 ⇒ F* wirkt in gleicher Richtung („drückt“) wie F1 bei x1 > 0
100
Mechanik – Schwingungen II
⇒ Nun sehen wir uns die Physik an:
·
·
∃ Hin- und Herfluten der Schwingungsenergie! → Schwebung
Dies beeinflusst von der Stärke der Kopplung, d.h. D* <> D
Für verschwindende Kopplung erhält man eine Lösung, die <15.2.> entspricht. (Dort hatten wir ja die Überlagerung zweier unabhängiger Schwingungen betrachtet!)
15.5.
−
Erzwungene Schwingungen
Die Differentialgleichung für den freien gedämpften Schwinger lautete:
D ⋅ x + k ⋅ x& + m ⋅ &x& = 0
å
â
æ
Feder-1 Reibungs- Trägheitskraft
−
(6 -16‘)
Jetzt versuchen wir, diesen Schwinger durch eine periodische äußere Kraft F
zum Schwingen anzuregen:
F = F0 ⋅ cos ωt
(7)
⇒ damit folgt für Gl. (6 - 16‘):
D ⋅ x + k ⋅ x& + m ⋅ &x& = F0 ⋅ cos ωt
−
Man könnte vermuten, dass das System bestrebt ist, mit der Frequenz ωGS des
gedämpften Schwingers zu schwingen:
ωGS =
−
(8)
D  k 
−

m  2m 
2
(6 - 22)
Erfahrung zeigt jedoch: nach gewisser Zeit (Einschwingzeit) erfolgt Schwingung
gemäß:
x = x 0 ⋅ cos (ωt − α)
(9)
Also: Mit Anregungsfrequenz ω, aber gegenüber F um α pasenverschoben.
−
(9) in (8) liefert:
Dx 0 cos (ωt − α) − kωx 0 sin (ωt − α) − mω 2 x 0 cos (ωt − α) = F0 cos ωt
1
(10)
allgemein: Rückstellkraft
101
Mechanik – Schwingungen II
−
Betrachtung von Gl. (10): |sin| und |cos| sind stets ≤ 1 ⇒ welche Glieder von Bedeutung sind, wird durch die Vorfaktoren entschieden.
D
. Für diesen Fall folgt aus Gl. (10):
m
a) ω <<
Dx 0 cos (ωt − α) = F0 cos ωt
x0 =
⇒
F0
; α=0
D
D
. Für diesen Fall folgt aus Gl. (10):
m
b) ω >>
− mω 2 x 0 cos (ωt − α) = F0 cos ωt
x0 =
⇒
F0
mω 2
; α = π (weil cos (ωt − α ) = − cos ωt ist)
c) Wir betrachten α =
π
. Für diesen Fall ist:
2
π

x& = −ωx 0 sin  ωt − 
2

= + ωx 0 cos ωt
~ F!
x& und F sind in Phase ⇒ maximaler Energieeintrag!
Also:
Leistung: Arbeit/Zeit
dA F ⋅ dx
=
= F ⋅ x&
dt
dt
J
[P] = ≡ W ... Watt
s
P=
(11)
SI
102
Mechanik – Schwingungen II
Die äußere Kraft leistet:
Pa = F ⋅ x&
F = F0 ⋅ cos ωt
x& = ωx 0 cos ωt
Pa = F0 ωx 0 cos 2 ωt
⇒
(12)
Die Reibungskraft verbraucht an Leistung:
PR = FR ⋅ x&
mit der Beziehung
FR = k&x
folgt
PR = kω 2 x 02 cos 2 ωt
(13)
Für Pa = PR folgt aus (12) und (13):
F0 ωx 0 = kω 2 x 02
π F

x0 α =  = 0
2  kω

⇒
(14)
Für diesen Fall sind das Reibungsglied und das Glied der äußeren Kraft in
Gl. (10) einander gleich, d.h., das Trägheits- und Rückstellglied müssen sich
zu Null ergänzen. Aus Gl. (10) folgt dann:
π
π !


Dx 0 cos  ωt −  − mω 2 x 0 cos  ωt −  = 0
2
2


π

ω α =  =
2

⇒
D
= ω 0 (Frequenz des ungedämpften Schwingers!)
m
(15)
Also war auch das ω in Gl. (14) identisch mit ω0
F
π

x0 α =  = 0
2  kω0

⇒
Diskussion:
·
·
π
Für ω = ω0 ist α = ⇒ maximaler Energieeintrag, maximales x0(ω)
2
Dieses maximale x0 steigt mit verringerter Dämpfung → Resonanzkatastrophe!
(14‘)
u
103
Mechanik – Wellen
16.
Wellen
16.1.
Einleitung
−
Beispiele:
gekoppelte Pendelreihe
Wellenmaschine
Seilwelle (hin und her)
n
·
Das schwingende Medium/Teilchen bewegt sich nicht fort,
sondern schwingt um eine Ruhelage.
!
·
Was sich fortbewegt/ausbreitet, ist der Schwingungszustand.
·
·
·
−
Was passiert?
⇒ experimentelles Modell:
⇒ Welle = räumliche Ausbreitung eines Schwingungszustandes
−
!
Welle in x-Richtung:
vPh = Geschwindigkeit der
Bewegung der Wellenberge, -täler usw.
−
Wie drückt man das mathematisch aus? Offenbar ist
y = f ( x, t )
und zwar genauer
y( x , t ) = f ( x − v Ph ⋅ t )
vPh ...Phasengeschwindigkeit, die Ausbreitungsgeschwindigkeit der Welle
(1)
Plausibilitätserklärung:
1.
Momentaufnahme bei t = 0:
2.
Zustand zum Zeitpunkt t = t1:
Also: Für jeden Punkt x ist y jetzt
so, „wie vorher um vPh ž t1
weiter links“!
104
Mechanik – Wellen
Der Schwingungszustand y(x, t) ist also nicht von x und t einzeln abhängig, sondern
von der Kombination x - vPh ž t. Dies ist die Phase der Welle, sie bestimmt y eindeutig.
!
(Eigentlich ist dies einfach Ausdruck der Tatsache, dass sich der Schwingungszustand mit vPh bewegt und dabei nicht verändert.)
−
Gl. (1) beschreibt eine Welle allgemein. Diese können auch nichtperiodische
Wellen sein (z. B. Seilwelle, Stoßwelle)!
−
Die größte Bedeutung haben harmonische Wellen (sin, cos), auf die wir uns
im Folgenden konzentrieren:
−
vPh für eine harmonische Welle ist
λ
= λ⋅ν
T
λ
=
⋅ω
2π
v Ph =
v Ph
!
ω = 2πν
(2)
Man definiert die Wellenzahl k
k=
2π
λ
(3)
(3) in (2) liefert somit
v Ph =
−
ω
k
(4)
Wie gleich plausibel gemacht wird, lautet die Wellenfunktion für eine harmonische Welle in x-Richtung
y( x , t ) = y 0 sin (ωt − kx )
(5)
Plausibilitätserklärung:
Offenbar ist der Schwingungszustand eindeutig festgelegt durch ωt − kx .
·
Dann muss das aber auch der Fall sein für
·
−
1
ω
⋅ (ωt − kx ) = x − ⋅ t
k
k
= x − v Ph ⋅ t
⇒ Das Argument der Sinusfunktion (Gl. (5)) drückt dasselbe Wechselspiel
zwischen räumlicher und zeitlicher Bewegung aus wie Gl. (1)!
105
Mechanik – Wellen
16.2.
−
Wellengleichungen
Wie sieht die Differentialgleichung aus, der eine Welle gehorcht?
Im eindimensionalen Fall, also für y = f(x, t), lautet sie:
∂2y
∂2y
2
=
v
⋅
Ph
∂t 2
∂x 2
(6)
Dies ist die d’ALEMBERTsche Wellengleichung.
−
Diese Gleichung wird von jeder Funktion y = f(x ± vPh t), also von jeder allgemeinen Wellenfunktion nach Gl. (1) erfüllt, nicht nur von Funktionen lt. Gl. (5)
für harmonische Wellen!
−
Andeutung des Beweises:
∂f ( x ± v Ph ⋅ t ) ∂f ( x ± v Ph ⋅ t ) ∂ ( x ± v Ph ⋅ t )
=
⋅
∂ ( x ± v Ph ⋅ t )
∂t
∂t
∂f ( x ± v Ph ⋅ t )
⋅ (± v Ph )
=
∂ ( x ± v Ph ⋅ t )
∂f ( x ± v Ph ⋅ t ) ∂f ( x ± v Ph ⋅ t ) ∂ ( x ± v Ph ⋅ t )
⋅
=
∂x
∂x
∂ ( x ± v Ph ⋅ t )
â
=1
(7)
(8)
aus (7) und (8) folgt somit
∂f
∂f
= ± v Ph ⋅
∂t
∂x
(9)
Leitet man Gl. (9) auf beiden Seiten noch einmal ab, erhält man Gl. (6).
16.3.
Arten von Wellen
–
Schwingung quer zur Ausbreitungsrichtung
→ Transversalwellen (z. B. bestimmte elastische Wellen in Festkörpern; elektromagnetische Wellen)
–
Schwingung längs zur Ausbreitungsrichtung
→ Longitudinalwellen (z. B. bestimmte
elastische Wellen in Festkörpern; Schallwellen in Gasen und Flüssigkeiten)
−
Transversalwellen: Die Formulierung „Schwingung ⊥ Ausbreitungsrichtung“ ist
nicht eindeutig!
!
106
Mechanik – Wellen
Entscheidend ist die Lage der Schwingungsrichtung/-ebene:
·
konstante Lage ⇒ linear polarisierte Welle
·
gleichmäßige Drehung ⇒ zirkular (elliptisch) polarisierte Welle
·
ansonsten: nicht polarisierte Wellen
−
Wellen sind eine sehr allgemeine Erscheinung (definiert über Gl. (1), (6)):
Seilwellen, Wellen in Membranen, .... Meist jedoch betrachtet: Wellen im Volumen (Festkörper, Gas, Flüssigkeit, Vakuum).
Physikalische Natur der Wellen kann verschieden sein: elastische Wellen,
Schallwellen, elektromagnetische Wellen, ...
−
Oberflächenwellen in Flüssigkeiten:
·
Teilchen bleiben praktisch
am Ort, was sich bewegt,
ist der Bewegungszustand
(also wie bei allen Wellen!)
·
Wasserteilchen führen kreisende Bewegung aus
Im Prinzip sehr komplexe Erscheinung, da beeinflusst von
·
·
·
−
der Wassertiefe,
dem Wind,
der Oberflächenspannung!
Oben: Teilchengeschwindigkeiten in der Wasserwelle, die der mitfahrende Beobachter feststellt.
Mitte: Teilchengeschwindigkeiten, die der ruhende
Beobachter in seinem System konstruiert.
Unten: Orbitalbewegung der Teilchen an der Oberfläche. ({2}, S. 184)
Unterteilung der Wellen nach der Geometrie ihrer Ausbreitung
(geometrischer Ort der Punkte gleicher Phase = Wellenfront):
·
ebene Welle
·
Zylinderwelle/Kreiswelle
·
Kugelwelle
16.4.
Wellenausbreitung in verschiedenen Medien
16.4.1. elastische Longitudinalwelle im Festkörper
−
Elastische Welle ist ein ständiges Wechselspiel von Dehnung (Auslenkung) und
Spannung.
Koordinate: x
Auslenkung: ξ = ξ(x)
107
Mechanik – Wellen
Wenn sich zwischen x und x + dx die Auslenkung ändert (d.h. ξ + dξ), heißt das,
dass dort eine elastische Spannung herrscht:
∂ξ
∂x
â
≡ ε (vgl. <11.1.>)
σ = E⋅
−
(10)
Wir betrachten ein Volumenelement im Festkörper:
Hinweis: Wir kümmern uns nicht
um Querkontraktion, betrachten
also eine sogenannte ebene Welle,
die „unendlich breit ist“.
σ( x + dx ) = σ( x ) +
∂σ
⋅ dx
∂x
(11)
Auf das Volumenelement dV = A ž dx wirkt nur die Differenz der Spannungen
bzw. Kräfte!
also:
links wirkt
Fl = σ( x ) ⋅ A
rechts wirkt
Fr = σ( x + dx ) ⋅ A = σ( x ) ⋅ A +
∂σ
⋅ dx ⋅ A
∂x
(11‘)
Die wirksame Nettokraft ist:
dF =
∂σ
⋅ dx ⋅ A
∂x
â
= dV
bzw. mit Gl. (10)
dF = E ⋅
∂ 2ξ
⋅ dV
∂x 2
(12)
Die Kraft führt zu einer Beschleunigung der in dV verkörperten Masse dm = ρ ž dV:
dF = dm ⋅
bzw.
dF = ρ ⋅
∂ 2ξ
∂t 2
∂ 2ξ
⋅ dV
∂t 2
(3 - 2‘)
(13)
108
Mechanik – Wellen
−
Gleichsetzung von (12) und (13):
⇒
∂ 2ξ E ∂ 2ξ
= ⋅
∂t 2 ρ ∂x 2
(14)
Dies ist der hier gültige Sonderfall von Gl. (6)!
−
Vergleich mit Gl. (6) liefert:
E
ρ
⇒
v Ph =
mit:
vPh ... Geschwindigkeit der longitudinalen Schallwelle im Festkörper
also:
Großes E / kleines ρ bedeutet große Schallgeschwindigkeit!
(15)
!
16.4.2. elastische Transversalwelle im Festkörper
−
Herleitung völlig analog zu <16.4.1.>, aber wegen Querdeformation ist G statt
E zu verwenden:
⇒
v Ph =
G
ρ
(16)
16.4.3. Schallwelle in Gasen (oder Flüssigkeiten)
−
... ist stets longitudinal ("Schermodul G = 0“)
−
Hier wiederum (weitgehend) analoge Herleitung, wobei anstelle von E der
Kompressionsmodul K zu verwenden ist. Man erhält:
⇒
−
K
=
ρ
1
κ⋅ρ
(17)
Aus Gl. (13 - 2) wissen wir, dass für Gase K = p ist (je größer p, desto schwerer ist
Gas komprimierbar). Nur für Gase (und nicht für Flüssigkeiten!) gilt deswegen1:
⇒
1
v Ph =
!
v Ph =
p
ρ
(17‘)
Das Problem der adiabatischen Zustandsänderung bei Gasen wird hier zunächst vernachlässigt (Gl.
(17‘) liefert eigentlich für v ≥ 1 kHz um einen Faktor
7 5 zu geringe Werte, vgl. <20.4.>).
109
Mechanik – Wellen
−
n
Beispiele:
Material
H2
Luft
Wasser
Al
Ti
Pb
(0°C)
(0°C)
(0°C)
(20°C)
(20°C)
(20°C)
Diamant
16.5.
−
vPh
1284
332
1402
(longitudinal)
m ž s-1
æ
( 14,4 ž 332 = 1260!)
m ž s-1
ä
m ž s-1
(4facher Wert von Luft!)
6420 m ž s-1
6070 m ž s-1
1960 m ž s-1
≈17000 m ž s-1
(ρ =2,7 g ž cm-3)
(ρ =4,5 g ž cm-3 ∧ größeres E)
(ρ =11,3 g ž cm-3 ∧ geringes E)
Spitzenwert!
Überlagerung von Wellen; Gruppengeschwindigkeit
Wellen überlagern sich ungestört (ungestörte Superposition). Mathematisch
„steckt das in der Linearität der d’ALEMBERTschen Wellengleichung (Gl. (6))“:
y1(t) ist Lösung
y2(t) ist Lösung



(6)
Linearität
 von
Gl.

→
y1(t) + y2(t) ist auch Lösung!
−
Voraussetzung: Auslenkung gering genug, damit die physikalischen Voraussetzungen noch stimmen, z.B. σ ~ ε (Gl. (10)), also HOOKEsches Verhalten, o.ä.1
−
Wellen können sich beim Überlagern verstärken oder schwächen (gegebenenfalls auslöschen).
Beispiele:
·
·
·
−
n
Chladnische Klangfiguren
Rubenssches Flammenrohr
Kundtsches Rohr
Stehende Wellen: Überlagerung hin- und herlaufender Wellen so, dass sich der
Schwingungszustand gar nicht mehr räumlich ausbreitet2.
!
Wenn man aber - auch bei einer transversalen stehenden Welle - „etwas dazwischenschiebt“, bricht die Welle ab. Es ist eben doch ein Hin und her, wenn auch ein
sehr spezielles!
Stehende Wellen haben große Beduetung: Akustik, Laser, Quantenmechanik ...
1
2
berühmte Ausnahme: Wechselwirkung sehr intensiver Laserstrahlung mit Materie
Die stehenden Wellen sind spezielle Lösungen der Wellengleichung unter gegebenen Randbedingungen
110
Mechanik – Wellen
−
−
Gruppengeschwindigkeit:
Eine harmonische Welle (ein ω!) überträgt kein Signal.
!
Ein Signal, z.B. ein Licht- oder Funkimpuls, ist aus vielen harmonischen Wellen
aufgebaut vorstellbar (FOURIER-Reihe!)
!
Beispiel (Modell): Überlagerung nur zweier harmonischer Wellen
n
a) ω; k
b) ω + ∆ω; k + ∆k
Sie überlagern sich konstruktiv, wenn ihre Phasen übereinstimmen, d.h. für
kx − ωt = (k + ∆k ) ⋅ x − (ω + ∆ω) ⋅ t
= kx + ∆kx − ωt − ∆ωt
⇒
!
∆kx = ∆ωt
(18)
(19)
Die Erfüllung der Bedingung (19) sichert also die Bildung und Erhaltung einer
Art „Mini-Impuls“:
·
·
bei t = 0 gilt dies für x = 0
∆ωt 1
bei t = t1 gilt dies für x1 =
∆k
⇒ Die Wellengruppe („Mini-Impuls“) bewegt sich also mit
v=
−
x 1 ∆ω
dω
=
→
t 1 ∆k
dk
Dies ist die Gruppengeschwindigkeit:
v Gr =
−
(20)
Wir hatten bereits kennengelernt
v Ph =
−
dω
dk
ω
, also ω = k ⋅ v Ph
k
(4), (4‘)
Wenn vPh für alle Wellenlängen (d.h. alle k) bzw. für alle Frequenzen den gleichen Wert hat, liefert Gl. (4‘)
111
Mechanik – Wellen
v Gr =
dω d (k ⋅ v Ph )
=
= v Ph
dk
dk
(21)
Dann sind also vGr und vPh gleich!
Beispiele dafür sind:
·
·
−
n
elektromagnetische Wellen im Vakuum
Schall in Luft
Oft ist aber vPh = f(ω) bzw. f(k), d.h. ω ~ k (Gl. (4‘)) gilt nicht mehr!
⇒ ∃ Dispersion!
Wellenpakete (Impulse) zerfließen / „dispergieren“, da jede harmonische
Elementarwelle ihre eigene Geschwindigkeit hat.
Beispiele für Dispersion:
·
Licht in Glas ⇒ vPh = f(ω), d.h. die Lichtgeschwindigkeit hängt von der Farbe ab!
·
Schall im Festkörper (Eis) ⇒ hohe Töne laufen schneller ("Piúh")
!
n
112
Mechanik – Wellenausbreitung
17.
Wellenausbreitung
Im Folgenden werden einige allgemeine Prinzipien / Beschreibungsmöglichkeiten /
Verhaltensweisen / Eigenschaften von Wellen behandelt. Sie gelten für alle Wellen.
Bei konkreten Wellen (z.B. Schall, Licht, Funkwellen, ...) treten allerdings bestimmte dieser Erscheinungen in unterschiedlicher Weise in den Vordergrund. Dort1
werden sie gegebenenfalls auch noch vertieft.
17.1.
−
... ist die Wechselwirkung einer Welle mit einem Hindernis. Sehr vielfältig!
·
·
·
·
−
Streuung
!
Lichtwelle an einem Staubkorn in der Luft
elastische Welle im Festkörper an einem Hohlraum (Luftblase) im Festkörper
Schallwelle an einem Hindernis („Kind hinter einem Baum“)
Wasserwelle am Pfahl im Wasser
kleines Hindernis,
a << λ:
⇒ Kugel-Streuwelle
(liefert Information über
Existenz des Hindernisses,
nicht über seine Form)
−
Hier also:
−
Gegensatz: Hindernis gibt Wellenenergie verzögert ab ⇒ konstante Phasenbeziehung geht verloren → inkohärente Streuung
17.2.
Hindernis als Streuzentrum; gestreute Welle hat feste Phasenbeziehung mit der Primärwelle → kohärente Streuung
Das HUYGENSsche Prinzip
(HUYGENS-FRESNELsches Prinzip)
−
Man kann Wellenausbreitung sehr gut verstehen, wenn man sich vorstellt, dass
jeder Punkt, der von einer Welle getroffen wird, wieder zum Ausgangspunkt einer
Kugel- (3D) oder Kreiswelle (2D) wird.
−
Dies ist trivial für ungestörte Wellenausbreitung, z.B. ebene Welle:
−
Interessant und lehrreich wird es, wenn Hindernisse auftreten:
1
!
d.h. an entsprechender Stelle im Rahmen der Vorlesung
113
Mechanik – Wellenausbreitung
−
Reflexion:
⇒ Einfallswinkel = Ausfallswinkel
−
Übergang in ein Medium mit
anderer Ausbreitungsgeschwindigkeit (Phasengeschwindigkeit):
v Ph ,1 =
v Ph , 2 =
λ1
AB
λ2
AB
λ1
T
λ2
T
= sin α
= sin β






⇒






⇒
v Ph ,1
v Ph , 2
λ1
=
λ2
AB
⋅
AB
AB
AB
v Ph ,1
v Ph , 2
=
sin α
sin β
(1)
Dies ist das aus der Optik bekannte Brechungsgesetz, das für alle Wellen gilt!
17.3.
Das FERMATsche Prinzip
−
Eine Welle läuft zwischen zwei Punkten immer so, dass sie dazu möglichst wenig Zeit braucht.
−
Sehr allgemeines Prinzip! Reflexions- und Brechungsgesetz sind Sonderfälle davon.
!
A → P → B ist kürzester Weg, weil
A‘ → P → B auf einer Gerade liegen.
Jedes A → Q → B wäre länger,
weil A‘ → Q → B länger ist!
Plausibilitätserklärung:
Weg lt. Brechungsgesetz nutzt die
höhere Phasengeschwindigkeit
bestmöglich aus.
114
Mechanik – Wellenausbreitung
−
Beispiel: geologische Untersuchung
n
Kommentar:
u
Jede der drei Wellen folgt für sich dem FERMATschen Prinzip:
a) die direkte Welle, die sich geradlinig ausbreitet,
b) die Mintrop-Welle, die die schnellste nicht-direkte Welle ist,
c) die sogenannte regulär reflektierte Welle, die existiert, weil an der Grenzfläche A ↔ B nicht alle Intensität durchgehen darf und die („für sich optimiert“) dem Reflexionsgesetz folgt.
−
Woher wissen die Wellen den kürzesten Weg?
Dies ist nicht leicht vorstellbar. Oft ist es zu erklären mit dem Argument, dass
die nicht optimalen Wellen destruktiv interferieren und sich auslöschen.
17.4.
Beugung
−
... ist die Eigenschaft von Wellen, in gewissem Maße hinter Hindernisse gelangen zu können.
!
−
Nur Hindernisse a >> λ werfen scharfen Schatten.
!
Beispiel:
n
→ Man kann eine Person hinter einem Baum hören (a), aber nicht sehen (b):
a) Schallwellen (Beispiel Kammerton a): 440 Hz ∧ 330 m ž s-1
330 m ⋅ s
⇒ λ=
= 0,75 m
440 s
b) Wellenlängenbereich für sichtbares Licht:
⇒ λ = 400 ... 700 nm.
−
allgemeine Deutung der Beugung
mit HUYGENSschem Prinzip:
115
Mechanik – Wellenausbreitung
−
etwas anspruchsvollere Erklärung über die Überlagerung von Wellen:
Der Gangunterschied der Wellen
rechts und links vom Spalt beträgt:
d ⋅ sin α ≈ d ⋅ α
Die Wellen löschen sich gegenseitig
aus, wenn α so groß wird, dass gilt:
d⋅α =
α Grenz =
⇒
λ
2
λ
λ
→ 1
2d
d
Die Breite x des „Eindringbereiches“ beträgt:
x = D ⋅ tan α ≈ D ⋅ α
λ
x = D⋅
∧
x ≈ d (Näherung)
d
x = D⋅λ
⇒
⇒
(2)
n
Beispiel:
Hindernisbreite 0,5 m (Baum) ∧ Abstand 0,5 m
·
Kammerton a: x = 0,61 m ⇒ Wellenfront "längst wieder geschlossen"
·
Licht (0,5 µm): x = 0,5 mm = typische Unschärfe eines Schattens
17.5.
−
DOPPLER-Effekt; MACHsche Wellen
Wellenerzeuger bewegt sich mit Geschwindigkeit v relativ zum Medium.
⇒ Welle läuft um vPh ž T
Quelle läuft um v ž T
⇒ λ verringert sich von:
auf:



!
während der Periodendauer T
λ = v Ph ⋅ T
λ ′ = ( v Ph − v) ⋅ T
(3)
⇒ ν erhöht sich auf:
ν′ =
1
v Ph
v Ph
=
=
λ′
( v Ph − v) ⋅ T
1
v
1−
v Ph
⋅ν
(4)
Bei Beachtung weiterer Einflüsse ist diese Annahme „sicherer“.
116
Mechanik – Wellenausbreitung
−
Wenn sich Wellenerzeuger vom Beobachter wegbewegt, sinkt ν auf:
ν′ =
1
v
1+
v Ph
⋅ν
(5)
Die Frequenzverschiebung lt. Gl. (4) bzw. (5) heißt DOPPLER-Effekt.
⇒ Geschwindigkeitsschätzung anhand Tonumschlags möglich! (Feuerwehr, Hupe)
−
·
Gl. (3), (4) und (5) betreffen die Bewegung der Quelle relativ zum Medium
und zum (im Medium ruhenden) Beobachter.
·
Eine relativ zum Medium ruhende Quelle bei
bewegtem Beobachter führt (bei einer Bewegung
auf die Quelle zu (+) bzw. von ihr weg (-)) auf:
·
−
u
Kommentar:

v 
 ⋅ ν
ν ′ = 1 ±
v

Ph 
(4‘)
Bei Lichtwellen gibt es ein solches Medium nicht und die Formeln Gl. (4)
und Gl. (4‘) verschmelzen!
MACHsche Wellen:
Für v ≤ vPh wird die Welle
vor Quelle mehr oder weniger zusammengedrängt:
Für v > vPh "türmen“ sich
die Wellenfronten zum
Überschallkegel auf:
Für den Öffnungswinkel α
des Kegels gilt:
v Ph
1
=
v
M
M ... MACHzahl
sin α =
(6)
Die Machzahl gibt an, wieviel Mal v größer als die Schallgeschwindigkeit vPh
(Phasengeschwindigkeit des Schalls) ist.
!
Der Überschallknall ist das Überstreichen des Ortes des Beobachters durch den
Kegel, kein einmaliges „Durchstoßen der Schallmauer“!
!
117
Mechanik – Wellenausbreitung
17.6.
Intensität einer Welle
−
Wir betrachten nun die von der Welle (pro Zeit- und Flächeneinheit) transportierte Energie, d.h. die Energiestromdichte bzw. Intensität der Welle.
−
Die Betrachtung erfolgt am Beispiel elastischer Wellen, gilt aber praktisch allgemein.
−
Es findet ein ständiges hin und her von Ekin und Epot statt (analog <6.1.>):
Grenzzustände:
1.
⇒
2.
ξ = ξ 0 (Auslenkung maximal)
ξ& ≡ v = 0
ξ = v 0 (Geschwindigkeit maximal)
also ξ = 0 (Nulldurchgang)



Eges = Epot, Ekin = 0



Eges = Ekin, Epot = 0
Die hier verwendete Geschwindigkeit v ≡ ξ& ist die sogenannte Schallschnelle, die
Geschwindigkeit des Schwingens. Sie darf nicht mit der Ausbreitungsgeschwindigkeit des Schwingungszustandes, d.h. der Ausbreitungsgeschwindigkeit der Welle, verwechselt werden.
−
Da Eges sowieso konstant ist, nehmen wir Grenzfall 2 für die Ermittlung der Gesamtenergie ∆W eines Volumenelementes ∆V mit der Masse ∆m:
∆W =
=
⇒
1
∆m ⋅ v 02
2
∆m = ρ ⋅ ∆V
1
ρ ∆V ⋅ v 02
2
∆W
1
≡ w = ρ ⋅ v 02
∆V
2
(7)
Die Energiedichte w („Energieinhalt der Welle“) bewegt sich mit der Ausbreitungsgeschwindigkeit vPh der Welle. Damit ergibt sich für die Intensität I
I ≡ w ⋅ v Ph =
1
v Ph ρ ⋅ v 02
2
(8)
Aus Grenzfall 1 erhält man analog:
I=
−
1
v Ph ρ ⋅ w 2 ⋅ ξ 02
2
Dies ist allgemeingültig: Die Intensität der Welle ist immer proportional dem
Quadrat der Amplitude!
(8‘)
!
118
Mechanik – Wellenausbreitung
−
Ohne Beweis: Das Produkt vPh ž ρ heißt Wellenwiderstand Z.
Z = v Ph ⋅ ρ
−
(9)
u
Kommentar:
Gl. (9) ist plausibel, da mit zunehmender vPh und zunehmendem ρ die „pro
Zeiteinheit in Schwingungen versetzte Masse ansteigt“, was den Ausbreitungswiderstand der Welle (pro Volumeneinheit) erhöht.
17.7.
−
Reflexion und Transmission an einer Grenzfläche
Wir betrachten das Verhalten einer Welle an der Grenzfläche zweier Medien:
gegeben:
Medium 1
Medium 2
v Ph ,1
v Ph , 2
ρ1
ρ2
⇒ Z1 = v Ph ,1 ⋅ ρ1
⇒ Z 2 = v Ph , 2 ⋅ ρ 2
Indizes:1
e - einfallend
d - durchgehend
r -reflektiert
−
Energiesatz an der Grenzfläche:
Ie = Ir + Id
(10)
bzw. mit Gl. (8) und (9):
1
1
1
Z1 v e2 = Z1 v 2r + Z 2 v d2
2
2
2
(11)
Gl. (11) umgestellt liefert:
⇒
−
Z1 ( v e2 − v 2r ) = Z 2 ⋅ v d2
Damit nicht unendlich große Deformationen auftreten, muss die Welle an der
Grenzfläche stetig sein, d.h. Auslenkung ξ und Geschwindigkeit ξ& = v müssen
links und rechts gleich sein:
⇒ (u.a.) v e + v r = v d
å
æ
Geschwindigkeit links Geschwindigkeit rechts
1
(12)
(13)
Der Index „0“ wird der Einfachheit halber weggelassen, d.h. v0, e ≡ ve, usw.
119
Mechanik – Wellenausbreitung
−
Gl. (12) und (13) aufgelöst nach vd bzw. vr ergibt:
⇒
−
vd = ve ⋅
2Z1
Z1 + Z 2
vr = ve ⋅
Z1 − Z 2
Z1 + Z 2
à (b)
(14)
Daraus schließlich ermittelbar:
Id ≡
Z1 ⋅ Z 2
1
Z 2 ⋅ v d2 = 4I e ⋅
2
( Z1 + Z 2 ) 2
( Z1 − Z 2 ) 2 à (a)
1
2
I r ≡ Z1 ⋅ v r = I e ⋅
2
( Z1 + Z 2 ) 2






Diskussion:
a) Im Allgemeinen ∃ Reflexion und Transmission.
Für Z1 = Z2 geht die gesamte Welle durch, d.h. die Reflexion wird Null.
Für Z1 << Z2 bzw. Z2 << Z1 geht Id → 0 (vollständige Reflexion).
b) Bei Z1 > Z2 (Übergang ins dünnere Medium) ist das Vorzeichen von vr
gleich dem von ve, d.h. die Welle wird mit gleicher Phase reflektiert.
Bei Z1 < Z2 ist das Vorzeichen von vr entgegengesetzt dem von ve, d.h., bei
der Reflexion am dichteren Medium gibt es einen Phasensprung um π.
(15)
u
!
!
!
Dies sind allgemeingültige Aussagen, die für alle Wellen gelten.
120
Mechanik – Akustik
18.
Akustik
18.1.
Einleitung
−
Akustik ist bis zu gewissem Grad am Menschen orientiert:
ν ≤ 16 Hz
16 Hz ≤ ν ≤ 16 kHz1
v > 16 kHz
Infraschall
hörbarer Schall
Ultraschall
−
Problem der Lautstärke: ∃ riesiger Intensitätsbereich, den das menschliche Ohr
auch tatsächlich in starkem Maße (1 : 1013) überstreicht.
−
Lösung: Intensität der Wahrnehmung (d.h. die Lautstärke) hängt vom Logarithmus der Schallintensität ab.
 I 
L = 10 ⋅ log  
 I0 
L ... Lautstärke
I0 ... gerade noch hörbare Intensität, Hörschwelle
log ... dekadischer Logarithmus
Maßeinheit:
⇒
[L] ... Phon oder Dezibel (db)
I = I0
I = 102 I0
I = 105 I0
I = 1013 I0
⇒
⇒
⇒
⇒
L= 0
L = 20
L = 50
L =130
SI
Phon
Phon
Phon
Phon
Hörschwelle
Flüstern
normales Sprechen
Schmerzschwelle
Kommentar:
Das Ohr erfasst 13 Zehnerpotenzen! Die untere Grenze liegt nahe der „Hörbarkeit
der Brownschen Bewegung“
18.2.
u
!
Töne und Klänge
−
Ton
= reine Sinusschwingung
−
Klang
= realer Ton eines Instrumentes, d.h. Sinus + Obertöne lt. FOURIER
−
Geräusch = nichtperiodischer Vorgang
1
(1)
Angabe der oberen Hörschwelle ist ein Mittelwert. Die tatsächliche Hörschwelle kann von 4 kHz
(Greis) biz zu 20 kHz (Kind) reichen.
121
Mechanik – Akustik
−
Mehrere Klänge (reale Töne) gleichzeitig klingen dann besonders harmonisch,
wenn sie viele Obertöne gemeinsam haben.
⇒ besonders gut klingt es, wenn
−
!
ν1
= 2 : 1 ist → Oktave
ν2
Tonleiter = Unterteilung der Oktave in 7 Zwischenstufen, so „dass es gut klingt“
C-Dur-Tonleiter:
Ton
νx
νc
νx
1
ν x −1
c
d
e
f
g
a
h
c
1
9/8
5/4
4/3
3/2
5/3
15/8
2
9/8
10/9
16/15
9/8
10/9
9/8
16/15
2
(große) (große)
(große) (große)
Sekunde Terz Quarte Quinte Sexte Septime Oktave
Intervall
Dies ist die so genannte reine Stimmung. Sie führt zu Problemen bei Instrumenten
mit fest eingestellten Tönen (z. B. Klavier):
Beispiel C-Dur:
D-Dur:
2. Ton d − Taste 9
=
=
(Frequenzverhältnis)
8
1. Ton
c − Taste
á
â
e − Taste 10
=
=
9
d − Taste
Um Tasteninstrumente für alle Tonarten nutzbar zu machen, verteilt man die unvermeidlichen Abweichungen gleichmäßig (so genannte temperierte Stimmung).
−
Oktave
= 5 Ganztonschritte + 2 Halbtonschritte = 6 Ganztonschritte
bisher war (reine Stimmung):
Ganztonschritt =
9
Halbtonschritt = 16
8
bzw. 10
9
= 1,125 bzw. 1,111
= 1,067
15
nun ist (temperierte Stimmung):
⇒ Ganztonschritt = Faktor
Halbtonschritt = Faktor
1
2
6
2 ≈ 1,12246
12
2 ≈ 1,05946



also konstantes Frequenzverhältnis von
Ton zu Ton
relative Frequenz
Frequenzverhältnis zum Nachbarton
122
Mechanik – Akustik
18.3.
Stehende Wellen; Musikinstrumente
−
Stehende elastische Wellen lassen sich durch Mehrfachreflexion (Hin- und
Herlaufen) im elastischen Medium erzeugen.
−
Bestimmend ist das Verhältnis der Wellenwiderstände am Ende des Mediums.
·
Beispiel:
An einem Ende Übergang zum größeren, am anderen Übergang zum kleineren
Wellenwiderstand, also einmal ein Phasensprung von π, einmal nicht.
!
n
mögliche physikalische Realisierungen:
1) einseitig eingespannter Stab der Länge l
2) einseitig offene Röhre der Länge l
Phasensprung π
kein Phasensprung
Knoten
Bauch
⇒
νn =
v Ph (2n − 1) ⋅ v Ph
=
λn
4l
l=
1
⋅ λ1
4
l=
3
⋅ λ2
4
l=
5
⋅ λ3
4















l
=
(2n − 1)
⋅ λn
4
(mit n = 1, 2, 3, ...)
(2)
Die νn sind die Eigenschwingungen, die sich bei geeigneter Anregung erzeugen lassen bzw. die als Obertöne stets in gewissem Maße mitschwingen.
·
Bei beidseitig gleichem (offenem oder geschlossenem) Ende ergibt sich
analog zu Gl. (2)
⇒
νn =
v Ph n ⋅ v Ph
=
λn
2l
(mit n = 1, 2, 3, ...)
(3)
3
1

also l =  , 1, , 2, K ⋅ λ
2
2

123
Mechanik – Akustik
Je nachdem, ob die Enden beide fest oder beide lose sind, ergeben sich unterschiedliche Schwingungsformen:
Oben:
Grund- und Oberschwingungen eines an beiden Enden freien, longitudinal
schwingenden Stabes
Unten: Longitudinalschwingungen eines Stabes
a) an einem Ende fest, am anderen frei
b) an beiden Enden fest
Die Verschiebungen in Richtung der Stabachse sind senkrecht zum Stab gezeichnet. (Verschiebung nach rechts - nach oben, Verschiebung nach links - nach unten). ({2}, S. 172)
−
u
Kommentar:
·
mögliche Realisierungen:
a) beidseitig eingespannte Saite
b) einseitig geschlossene Röhren
c) effektiv beidseitig offene Röhren
·
konisches Ende „wirkt wie offenes“
124
Mechanik – Akustik
Beispiele
zu a) Geige
zu b) viele Blasinstrumente, z.B. Klarinette (gerade Obertöne fehlen zum
Teil - vgl. Gl. (2))
·
zu c) Oboe (alle Obertöne vorhanden - vgl. Gl. (3))
·
·
Instrumente besitzen in der Regel „Erreger“ (Lippen des Bläsers, Schilfrohr
bei Holzblasinstrumenten, Geigenbogen). Es erfolgt eine „Selektion“ und
Formung des Tons über Resonanz (Luftsäule, Geigensaite).
·
In Gl. (2) und (3) steht vPh! Dies hat Auswirkungen:
Bei Gasen war:
v Ph =
⇒
p ~N
ρ ~ N ⋅ M mol
⇒
ρ = ρ( T )
p
ρ
(16 -17‘)



⇒ Tonhöhe vom Gas abhängig!
(Beispiel Tonhöhen in He und O2)
!
⇒ Einfluss der Temperatur
125
Literaturliste
LITERATURLISTE
Titel
Autoren
Verlag
ISBN
DM
Physik
Gerthsen; Vogel
Springer
3-540-65479-8
129,-
Physik in Experimenten
und Beispielen
Paus, Hans J.
Hanser
3-446-17371-4
98,-
Experimentalphysik 1
Mechanik und Wärme
Demtröder, W.
Springer
3-540-57095-0
64,-
Experimentalphysik 2
Elektrizität und Optik
Demtröder, W.
Springer
3-540-56543-4
64,-
Physics Principles & Applications
Harris; Hemmerling; Mallmann
McGraw-Hill
0-07-026851-7
Physik (Teil 1)
Halliday, David;
Resnick, Robert
de Gruyter
3-11-010640-X
98,-
Physik (Teil 2)
Halliday, David;
Resnick, Robert
de Gruyter
3-11-013897-2
128,-
Physik und ihre Anwendungen
in Technik und Umwelt
Leute, Ulrich
Hanser
3-446-17232-7
58,-
Physik
Tipler, Paul A.
Spektrum
3-86025-122-8
128,-
Physik für Ingenieure
Lindner, Helmut
Fachbuch-Verlag
3-343-00772-2
48,-
Physik für Ingenieure
Hering; Martin;
Stohrer
Springer
3-540-62442-2
78,-
Mechanik, Akustik, Wärme; Bd. 1
Bergmann; Schae- de Gruyter
fer
3-11-012870-5
148,-
CD-ROM: CliXX Physik
Bauer; Benenson;
Westfall
Harri Deutsch
3-8171-1553-9
ca. 50,-
Taschenbuch der Physik
Stöcker
Harri Deutsch
3-8171-1556-3
58,-
Taschenbuch der Physik
Kuchling, H.
Fachbuch-Verlag
3-446-21054-7
40,-
V
Quellenverzeichnis
QUELLENVERZEICHNIS
{1}
Wolfgang Demtröder, Experimentalphysik 1, Berlin; Heidelberg; New York; London; Paris; Tokyo; Hong Kong; Barcelona; Budapest (Springer), 1994
{2}
Christian Gerthsen, Helmut Vogel, Physik, Berlin; Heidelberg; New York; London;
Paris; Tokyo; Hong Kong; Barcelona; Budapest (Springer), 17. Auflage 1993
VI
Sachregister
SACHREGISTER
A
abgeschlossenes System 19
Aktionsprinzip 16, 17
Akustik 121–5
aperiodischer Grenzfall 40
Arbeit 23–27
Beschleunigungs- 24
Hub- 24
mechanische 23
Auftrieb 76
dynamischer 95
Ausbreitungsgeschwindigkeit 104
B
Bahnkurve 9
barometrische Höhenformel 83
Benetzung 79, 80
BERNOULLIsche Gleichung 93
Beschleunigung 10
mittlere 10
Momentan- 10
Normal- 11
Tangential- 10
Beugung 115
Bewegung
geradlinig gleichförmig 15
gleichmäßig beschleunigt 19
Kreis- 11, 20
Bewegungsgleichung
Drehschwinger 56
erzwungene Schwingung 101
Federschwinger 34
gedämpfter Federschwinger 38
gekoppelter Federschwinger 100
mathematisches Pendel 37
Bezugssysteme
bewegte 47–51
körperfeste 60
Laborsystem 43
linear beschleunigte 48–49
mit konstanter Relativgeschwindigkeit 47
rotierende 49–51
Schwerpunktsystem 45
Brechung 114
C
Corioliskraft 51
D
Dehnung 65
Dichte 52
Dispersion 112
DOPPLER-Effekt 116
Drehimpuls 28, 57
Drehimpulssatz 30, 57
Drehmoment 29, 53
Drehschwingung siehe Schwingung
Druck
Schwere- 75
statischer 73, 94
Dynamik 15–22
E
Eigenschwingung 123
Elastizitätsmodul 65
Energie 23–27
kinetische 24, 35, 54
mechanische 23–24, 27
potentielle 24, 25, 32, 36
Energiedichte 118
Energiesatz
der Mechanik 27
Energiestromdichte 118
F
Federkonstante 34
Federkraft 34
Federschwinger 34
FERMATsches Prinzip 114
Flächenträgheitsmoment 70
FOURIER-Reihe 99
Frequenz 20
G
Galilei-Transformation 47
Geräusch 121
Geschwindigkeit 9
Gruppen- 111
mittlere 10
Momentan- 10
Gesetz
von BOYLE-MARIOTTE 82
Gleitreibung 21
VII
Sachregister
Goldene Regel der Mechanik 23, 75
Gravitationsfeld 31
Gravitationsgesetz 30
Gravitationskraft 31
Gravitationspotential 32
Gruppengeschwindigeit siehe Geschwindigkeit
H
Haftreibung 22
Haftreibungskoeffizent 22
HAGEN-POISEUILLEsches Gesetz 88
Hauptträgheitsachsen 60
Hauptträgheitsmomente 60
HOOKEsches Gesetz 65
Hörschwelle 121
HUYGENSsches Prinzip 113
Hysterese
elastische 71
I
Impuls 18
Impulserhaltung 19
Impulssatz 41
Inertialsysteme 48
innere Reibung 86–87
Intensität 118
K
Kapillarität 80
kartesische Koordinaten siehe Koordinaten
Kavitation 95
KEPLERsche Gesetze 32
Kinematik 9–14
kinetische Energie siehe Energie siehe Energie
Klang 121
Kohärenz 113
Kompressibilität 74, 82
Kompressionsmodul 66, 74
konservatives Kraftfeld siehe Potentialfeld
Kontinuitätsgleichung 85
Koordinaten
kartesische 9, 13
Polar- 11
Zylinder- 12
Kraft 15
Kräftepaar 53
Kraftfeld 16, 25
Kreisbewegung siehe Bewegung
Kreisel 62
Kreisfrequenz 20
Kriechfall 40
L
Laborsystem siehe Bezugssysteme
Länge 3
Lautstärke 121
Leistung 102
Linienspannung 78
LISSAJOUS-Figuren 97
Longitudinalwelle siehe Welle
M
MACHkegel 117
MACHsche Welle 117
MACHzahl 117
Masse 6, 52
Massepunkt 9
momentane Drehachse 63
N
Nabla-Operator 26
NEWTONsche Axiome 17
Normalbeschleunigung siehe Beschleunigung
Nutation 62, 63
O
Oberflächenenergie 78
spezifische 77
Oberflächenspannung 78
Oberton 99, 121
Ortsvektor 9
P
Paradoxon
hydrodynamisches 94
hydrostatisches 75
Pendel
mathematisches 37
Phase 105
Phasengeschwindigkeit 104
Phasensprung 120
Phasenverschiebung 101
Planetenbewegung 32
POISSONzahl 66
Polarisation 107
Polarkoordinaten siehe Koordinaten
Potentialfeld 25
potentielle Energie siehe Energie
Präzession 64
Präzessionsfrequenz 64
Punktmasse 4
VIII
Sachregister
Q
Querkontraktion 66
R
Raumwinkel 7
Reaktionsprinzip 17
Reflexion 114, 120
Reibkoeffizent 21
Reibungskraft 86
Resonanz 103
REYNOLDsche Zahl 89
Richtmoment 56, 69
Rotation 11, 52–58, 59–64
Rotationsenergie 54
S
Satz von STEINER 55
Schall 121
Schallgeschwindigkeit 109
Schallschnelle 118
Schermodul 67
Scherspannung 67
Scherwinkel 67
Schwebung 97, 101
schwere Masse 31
Schweredruck siehe Druck
Schwerpunkt 41, 52
Schwerpunktsystem siehe Bezugssysteme
Schwingung 34–40
Dreh- 56
erzwungene 101–3
Fundamental- 100
gedämpfte 38–40
gekoppelte 100
harmonische 36
Torsions- 56
SI-System 3
Spannung 65
Spannungs-Dehnungs-Diagramm 71
starrer Körper 52
statischer Druck siehe Druck
Staudruck 94
Stoß 42–46
elastisch 43–45
inelastisch 45
nichtzentral 46
zentral 43
Stoßparameter 46
Streuung 113
Stromlinien 85
Stromröhre 85
Strömung
ähnliche 90
laminar 87
stationär 85
turbulente 89
Strömungsgrenzschicht 90
Strömungswiderstand 95–96
Superposition 110
T
Tangentialbeschleunigung siehe Beschleunigung
Temperatur 6
Ton 121
Tonleiter 122
Torsion 68
Torsionsschwingung siehe Schwingung
Torsionswinkel 68
träge Masse 16, 31
Trägheit 15
Trägheitskraft 49
Trägheitsmoment 54
Trägheitsprinzip 15, 17
Trägheitstensor 59
Translationsenergie 24
Transmission 120
Transversalwelle siehe Welle
Ü
Überschallknall 117
Umdrehungsfrequenz siehe Frequenz
Umlaufbeschleunigung 12
Umlaufgeschwindigkeit 12
Umlaufzeit 20
V
Viskosität 22, 86
Volumenstrom 85
W
Welle 104
elastische 108, 109, 123
elliptisch polarisierte 107
harmonische 105
linear polarisierte 107
Longitudinal- 106, 108, 109
Schall- 109
stehende 110, 123
Transversal- 106, 109
zirkular polarisierte 107
Wellenfront 107
Wellengleichung 106
Wellenwiderstand 119
Wellenzahl 105
Widerstandsbeiwert 95
Winkel 7
Winkelbeschleunigung 12
Winkelgeschwindigkeit 12, 20
IX
Sachregister
Z
Zeit 6
Zentralfeld 25, 30
Zentrifugalkraft 49
Zentripetalkraft 21
Zylinderkoordinaten siehe Koordinaten
X