Grundrechnungsarten mit Brüchen Rettungsring Unechte Brüche

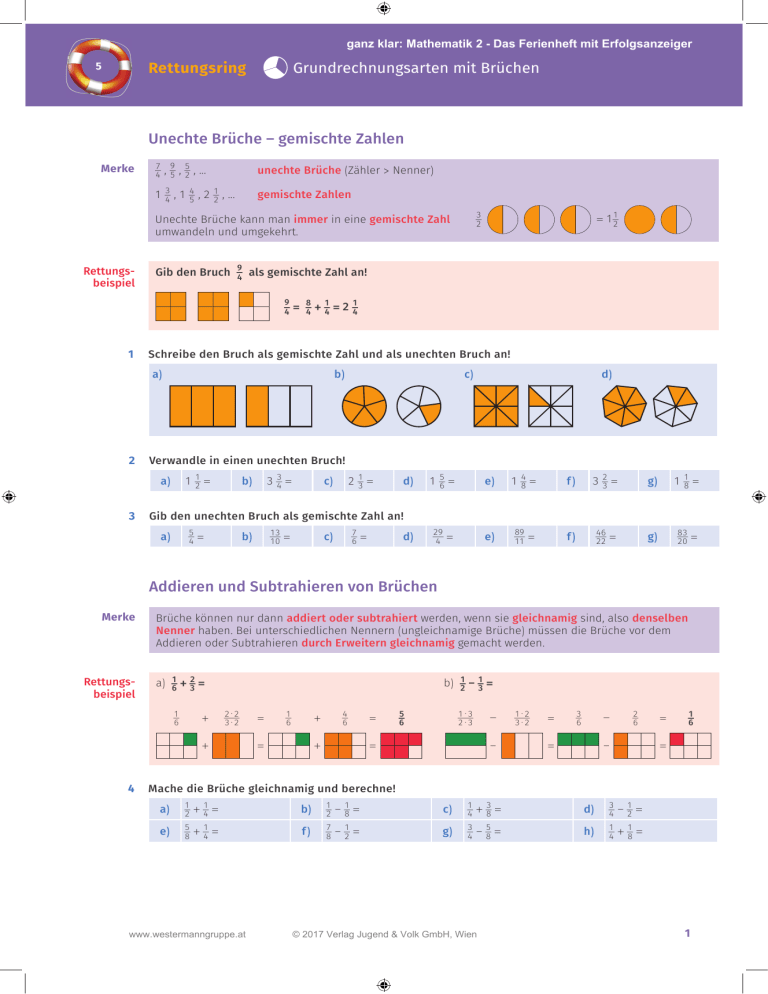
ganz klar: Mathematik 2 - Das Ferienheft mit Erfolgsanzeiger
Grundrechnungsarten mit Brüchen
Rettungsring
5
Unechte Brüche – gemischte Zahlen
Merke
9 _
5
7 _
_
4 , 5 , 2 , ...
unechte Brüche (Zähler > Nenner)
1 _34 , 1 _45 , 2 _12 , ...
gemischte Zahlen
3
_
Unechte Brüche kann man immer in eine gemischte Zahl
umwandeln und umgekehrt.
Rettungsbeispiel
Gib den Bruch _94 als gemischte Zahl an!
9
_
4
1
= _84 + _14 = 2 _14
Schreibe den Bruch als gemischte Zahl und als unechten Bruch an!
a)
2
b)
c)
d)
Verwandle in einen unechten Bruch!
1 _12 =
a)
3
= 1_12
2
3 _34 =
b)
2 _13 =
c)
d)
1 _56 =
e)
1 _48 =
3 _23 =
f)
1 _18 =
g)
Gib den unechten Bruch als gemischte Zahl an!
5
_
a)
4
=
13
_
b)
10
=
7
_
c)
6
=
d)
29
_
4
=
e)
89
_
11
=
46
_
f)
=
22
83
_
g)
=
20
Addieren und Subtrahieren von Brüchen
Merke
Rettungsbeispiel
Brüche können nur dann addiert oder subtrahiert werden, wenn sie gleichnamig sind, also denselben
Nenner haben. Bei unterschiedlichen Nennern (ungleichnamige Brüche) müssen die Brüche vor dem
Addieren oder Subtrahieren durch Erweitern gleichnamig gemacht werden.
a) _61 + _32 =
1
_
+
6
b) _21 – _31 =
2⋅2
_
3⋅2
+
4
=
1
_
4
_
+
6
=
6
+
=
5
_
1⋅3
_
6
−
2⋅3
=
–
1⋅2
_
3⋅2
=
3
_
−
6
=
2
_
6
–
=
1
_
6
=
Mache die Brüche gleichnamig und berechne!
a)
1
1
_
_
2 + 4 =
b)
1
_
– _18 =
c)
1
_
+ _38 =
d)
3
_
– _21 =
e)
5
_
f)
7
_
– _12 =
g)
3
_
– _58 =
h)
1
_
+ _18 =
8
+ _14 =
www.westermanngruppe.at
2
8
4
4
© 2017 Verlag Jugend & Volk GmbH, Wien
4
4
1
ganz klar: Mathematik 2 - Das Ferienheft mit Erfolgsanzeiger
Grundrechnungsarten mit Brüchen
Rettungsring
5
5
6
Achtung, hier müssen beide Brüche erweitert werden!
a)
1
_
+ _13 =
b)
2
_
– _38 =
c)
5
_
+ _35 =
d)
3
_
– _16 =
e)
1
_
3
+_
10 =
f)
1
_
+ _13 =
g)
6
_
– _12 =
h)
3
_
+ _14 =
2
4
3
5
6
7
4
5
Die Buchstaben der richtigen Lösungen ergeben ein Lösungswort!
1.
5
_
2.
2
_
3
– _19 =
3.
1
_
2
_
4.
3
_
5.
2
_
14
5
+
10
5
+ _17 =
6
–
+
=
1
_
8
1
_
3
=
=
6.
1
_
7.
7
_
8.
5
_
9.
5
_
10.
1
_
6
8
9
7
9
+ _38 =
11 H
_
1
+_
12 =
–
1
_
–
2
_
+
3
_
3
9
4
15
=
13
_
=
24
23
_
24
31
_
M
8
_
Ü
36
15
2
_
C
9
5 T
_
E
9
7
_
1
_
S
2
=
E
40
C
Addieren und Subtrahieren von gemischten Zahlen
Merke
Beim Addieren und Subtrahieren gemischter Zahlen werden
1
9
5
5
⋅4
4
_
_
_
_
_
3 _12 _
⋅4 + 1 8 = 3 8 + 1 8 = 4 8 = 5 8
1. die Brüche auf den gleichen Nenner gebracht,
2. die Ganzen addiert bzw. subtrahiert,
3. die Brüche addiert bzw. subtrahiert
4. und dann das Ergebnis vereinfacht.
Rettungsbeispiel
Von 4 _16 m Stoff werden 1 _23 m verkauft. Wie viel Stoff ist noch übrig?
1
3
7
⋅2
1
4
4
_
_
_
_
_
_
4 _16 – 1 _23 _
⋅2 = 4 6 – 1 6 = 3 6 − 1 6 = 2 6 = 2 2 m
Antwort: Es sind noch 2,5 m Stoff übrig.
7
8
9
2
Berechne und vereinfache die Ergebnisse so weit als möglich!
a)
5 _78 – 2 _18 =
b)
7 _57 + 1 _37 =
c)
3
1
_
5_
10 – 1 10 =
d)
7
7
_
4_
12 + 12 =
e)
2 _56 – 1 _16 =
f)
7 _49 + 3 _79 =
g)
10 _45 – 7 _35 =
h)
2 _56 + 4 _56 =
Berechne und vereinfache die Ergebnisse so weit als möglich!
a)
1 _13 + 2 _34 =
b)
2 _56 + _35 =
c)
4 _13 – _35 =
d)
1 _38 + 2 _31 =
e)
3 _27 + _34 =
f)
5 _34 – _16 =
g)
2 _35 – _78 =
h)
2
_
3
+ 1 _57 =
Ein Kübel Orangen wog 12 _12 kg, der leere Kübel _45 kg. Wie viel kg Orangen waren in dem Kübel?
www.westermanngruppe.at
© 2017 Verlag Jugend & Volk GmbH, Wien
31
_
63
K
ganz klar: Mathematik 2 - Das Ferienheft mit Erfolgsanzeiger
Grundrechnungsarten mit Brüchen
Rettungsring
5
Kürzen von Brüchen
Merke
Rettungsbeispiel
Durch das Kürzen wird ein Bruch mit kleineren Zahlen ausgedrückt.
Beim Kürzen werden Zähler und Nenner durch dieselbe Zahl (≠ 0) dividiert.
Der Wert des Bruches bleibt gleich.
5
Kürze den Bruch _
!
10
÷5
5
_
1
_
=
10
2
÷5
10
Durch welche Zahl wurde gekürzt?
÷
a)
6
_
=
10
÷
b)
3
_
10
_
5
15
÷
11
12
=
÷
c)
2
_
8
_
3
=
12
÷
÷
d)
4
_
25
_
6
35
÷
=
5
_
7
÷
Kürze die folgenden Dezimalbrüche!
a)
4
_
e)
12
_
i)
50
_
10
100
100
b)
6
_
f)
8
_
j)
25
_
100
10
1000
c)
4
_
d)
5
_
g)
25
_
h)
50
_
40
_
l)
125
_
k)
c)
14
_
d)
8
_
g)
48
_
h)
15
_
k)
32
_
l)
80
_
1000
100
1000
100
1000
1000
Kürze die Brüche so weit wie möglich!
a)
8
_
e)
32
_
i)
75
_
12
60
125
b)
16
_
f)
15
_
j)
42
_
12
35
60
24
42
120
36
60
120
Dividieren von Brüchen
Merke
Vertauscht man bei einem Bruch den Zähler mit dem Nenner, so erhält man den Kehrwert (reziproken Wert)
des Bruches.
3
5
5
3
3
_
5
5
_
3
5
_
3
ist der Kehrwert von _35 .
Brüche werden dividiert, indem man den ersten Bruch mit dem Kehrwert des zweiten Bruches multipliziert.
Rettungsbeispiel
9
Dividiere _
durch _35 !
10
9 _
3
_
10 ÷ 5
⋅3
⋅1
⋅2
⋅1
9 _
5
3
1
_
_
=_
10 ⋅ 3 = 2 = 1 2
www.westermanngruppe.at
d
Das bedeutet allgemein: _ba ÷ _dc = _ba ⋅ _
(b, c, d ≠ 0)
c
© 2017 Verlag Jugend & Volk GmbH, Wien
3
ganz klar: Mathematik 2 - Das Ferienheft mit Erfolgsanzeiger
13
14
15
Grundrechnungsarten mit Brüchen
Rettungsring
5
Berechne die Division!
a)
5
4 _
_
7÷9
=
b)
6 _
5
_
e)
1 _
4
_
=
f)
9 _
1
_
2÷5
7÷6
=
10 ÷ 4
=
c)
3 _
8
_
g)
5 _
2
_
9 ÷ 11
c)
8 _
4
_
g)
64 _
112
_
4÷5
d)
7 _
1
_
=
h)
5 _
3
_
12 ÷ 7
=
=
d)
9 _
3
_
=
h)
95
57 _
_
=
8÷6
=
Berechne und vergiss nicht zu kürzen!
a)
2 _
4
_
e)
25 _
5
_
3÷9
=
32 ÷ 8
=
b)
6 _
3
_
f)
3 _
27
_
5 ÷ 10
=
50 ÷ 120
=
14 ÷ 7
34 ÷ 119
=
10 ÷ 5
60 ÷ 108
=
Frau Sommer hat 16 _12 l Melissensaft zubereitet und füllt ihn in _34 -l-Flaschen ab. Wie viele dieser Flaschen
benötigt Frau Sommer zum Abfüllen des Melissensaftes?
Bruchteile berechnen
Merke
Rettungsbeispiel
Vom Ganzen zum Bruchteil
Vom Bruchteil zum Ganzen
3
_
von 6 cm = ?
4
2
_
von ? = 4 cm
3
Viertle das Ganze!
6 cm : 4 = 1,5 cm … 1,5 cm sind _14 des Ganzen!
Teile die Größe durch den Zähler!
4 cm : 2 = 2 cm … 2 cm sind _13 des Ganzen!
Nimm 3 Teile davon!
1,5 cm · 3 = 4,5 cm
Multipliziere mit dem Nenner!
2 cm · 3 = 6 cm
Eine „von“-Rechnung bei Brüchen ist
immer eine Multiplikation mit Brüchen.
3
_
4 ⋅6 = 4,5
Eine „sind“-Rechnung bei Brüchen ist
immer eine Division mit Brüchen.
4 ÷ _23 = 6
a) _34 von den 24 Kindern der Klasse sind Buben.
Wie viele Buben sind das?
Wie lang ist die Strecke insgesamt?
÷4
3
_
4 ⋅24
÷4
= _31 ⋅6 = 18
8,7÷_38 = 8,7⋅_83 = 23,2 km
A: In der Klasse sind 18 Buben.
16
17
4
b) 8,7 km sind _38 der Gesamtstrecke.
A: Die Strecke ist 23,2 km lang.
Berechne den Bruchteil!
a)
1
_
von 24 kg
b)
1
_
von 32 m
c)
1
_
von 27 cm
d)
1
_
von 45 t
e)
5
_
von 40 g
f)
2
_
von 60 l
g)
4
_
von 63 t
h)
1
_
von 72 h
sind 21 dag
2
8
4
5
3
7
5
3
Berechne das Ganze!
a)
1
_
sind 40 €
b)
1
_
sind 12 m
c)
1
_
sind 7 kg
d)
1
_
e)
7
_
sind 49 h
f)
4
_
sind 100 t
g)
4
_
sind 44 g
h)
6
_
2
8
www.westermanngruppe.at
3
5
4
9
© 2017 Verlag Jugend & Volk GmbH, Wien
6
11
sind 42 kg
ganz klar: Mathematik 2 - Das Ferienheft mit Erfolgsanzeiger
Grundrechnungsarten mit Brüchen
Rettungsring
5
Lösungen
1
a)
4
_
2
a)
3
_
2
b)
15
_
c)
7
_
3
d)
11
_
6
e)
12
_
f)
11
_
g)
9
_
3
a)
1 _14
b)
3
1_
10
c)
1 _16
d)
7 _14
e)
1
8_
11
f)
2
2_
22
g)
3
4_
20
4
a)
3
_
5
6
7
8
9
3
= 1 _13
b)
4
6
_
5
b)
3
_
e)
7
_
a)
5
_
e)
11
_
4
8
6
20
= 1 _15
c)
9
_
8
c)
5
_
f)
3
_
b)
7
_
= 1 _18
9
_
d)
8
7
= 1 _72
3
d)
1
_
g)
1
_
8
h)
3
_
c)
13
1_
30
d)
7
_
f)
8
_
15
g)
5
_
14
h)
17
_
8
8
24
8
4
8
12
20
Lösungswort: STECHMÜCKE
a)
3 _34
b)
9 _17
c)
4 _15
d)
5 _16
e)
1 _23
f)
11 _29
g)
3 _15
h)
7 _23
a)
1
4_
12
b)
13
3_
30
c)
11
3_
15
d)
17
3_
24
e)
1
4_
28
f)
7
5_
12
g)
29
1_
40
h)
8
2_
21
7
In dem Kübel waren 11 _
10 kg Orangen.
10
a)
2
b)
5
c)
2
d)
5
11
a)
2
_
b)
3
_
c)
1
_
250
d)
1
_
e)
3
_
25
f)
4
_
5
g)
1
_
4
h)
1
_
i)
1
_
j)
1
_
k)
1
_
l)
1
_
a)
2
_
b)
4
_
c)
7
_
d)
2
_
e)
8
_
f)
3
_
g)
8
_
h)
1
_
i)
3
_
j)
7
_
10
k)
4
_
l)
2
_
12
13
8
5
2
3
15
5
50
40
3
7
25
12
7
15
20
20
8
9
4
3
a)
1
1_
35
b)
1
1_
35
c)
15
_
32
d)
5 _14
e)
5
_
f)
3 _35
g)
1
3_
18
h)
35
_
8
www.westermanngruppe.at
© 2017 Verlag Jugend & Volk GmbH, Wien
36
5
ganz klar: Mathematik 2 - Das Ferienheft mit Erfolgsanzeiger
14
15
16
17
6
Grundrechnungsarten mit Brüchen
Rettungsring
5
a)
1 _12
b)
4
c)
1
d)
1 _12
e)
1 _14
f)
4
_
g)
2
h)
2
1_
25
15
Frau Sommer benötigt 22 Flaschen.
a)
12 kg
b)
8m
c)
9 cm
d)
9t
e)
25 g
f)
24 l
g)
36 t
h)
24 h
a)
80 €
b)
36 m
c)
28 kg
d)
126 dag
e)
56 h
f)
125 t
g)
99 g
h)
77 kg
www.westermanngruppe.at
© 2017 Verlag Jugend & Volk GmbH, Wien