5. Aufgabenblatt

INSTITUT FÜR ANGEWANDTE MATHEMATIK
DER UNIVERSITÄT ERLANGEN-NÜRNBERG
Prof. Dr. W. Merz
Erlangen, den 20.05.2009
5. Aufgabenblatt
zur Vorlesung “Mathematik für Ingenieure IV”
Info, CBI, LSE, EEI
Abgabe: In der Vorlesung der darauffolgenden Woche!
A17) Ein Mann und eine Frau vereinbaren ein Treffen zwischen 8 Uhr und 9 Uhr.
Die Eintreffzeiten seien gleichverteilt und hängen nicht voneinander ab. Der Mann
beschließt, 20 min auf die Frau zu warten, die Frau möchte höchstens 10 min warten.
Wie groß ist die Wahrscheinlichkeit, dass das Treffen zustandekommt?
6 Punkte
Lösungsvorschlag: Die Eintreffzeiten x des Mannes und y der Frau sind gleichverteilt
auf dem Intervall [0, 1], wenn man als Zeiteinheit eine Stunde nimmt. Der Ereignisraum
ist also Ω = [0, 1]2 . Das Treffen kommt zustande, wenn das Ereignis (x, y) die Bedingungen
x≤y
(der Mann kommt vor der Frau an) und
y − x ≤ 1/3 (die Frau kommt höchstens 20min später)
oder
y≤x
x − y ≤ 1/6
(die Frau ist zuerst da) und
(der Mann kommt höchstens 10min später)
erfüllt. Dies ist charakterisiert durch
(x, y) ∈ A := {(x, y) ∈ [0, 1]2 | − 1/6 ≤ y − x ≤ 1/3}.
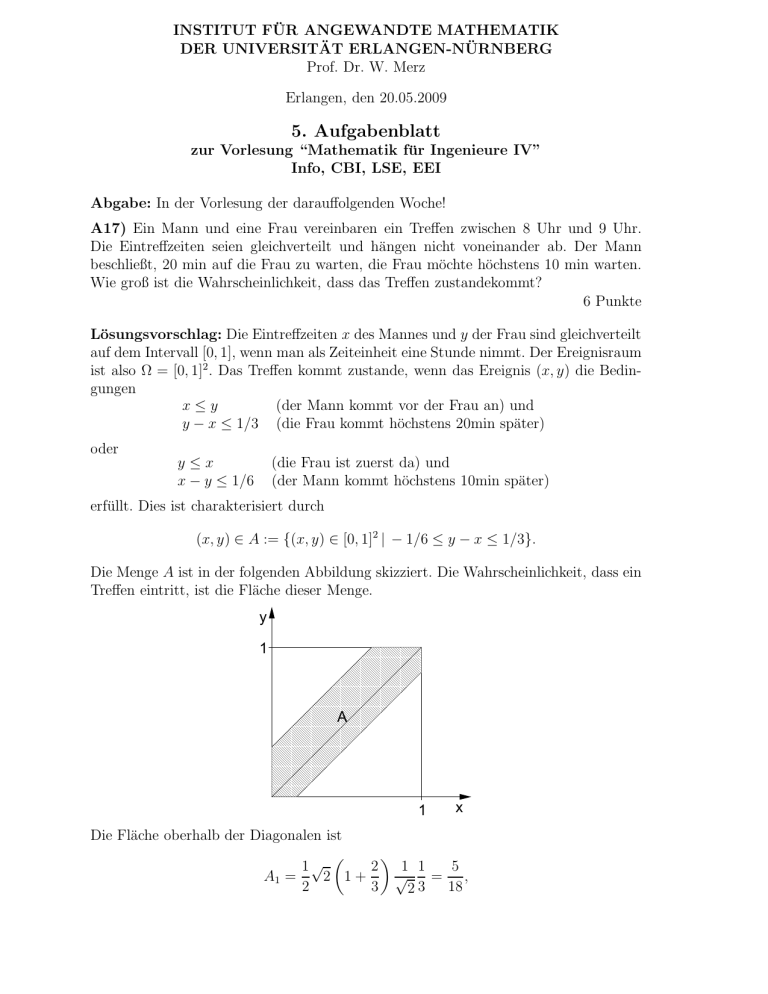
Die Menge A ist in der folgenden Abbildung skizziert. Die Wahrscheinlichkeit, dass ein
Treffen eintritt, ist die Fläche dieser Menge.
y
0000000000000000
1 1111111111111111
0000000000000000
1111111111111111
1111111111111111
0000000000000000
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
A
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
1
x
Die Fläche oberhalb der Diagonalen ist
2
1 1
5
1√
√
2 1+
= ,
A1 =
2
3
18
23
diejenige unterhalb der Diagonalen
1√
1 1
11
5
√
A2 =
= .
2 1+
2
6
72
26
Insgesamt hat man
p = |A| = A1 + A2 =
31
.
72
A18) Zwei reelle Zahlen x und y werden zufällig und unabhängig voneinander aus dem
Intervall [0, 1] ausgewählt. Berechnen Sie die Wahrscheinlichkeit des Ereignisses
“Der Abstand der Punkte beträgt höchstens t”
für t ∈ [0, 1].
6 Punkte
Lösungsvorschlag:
Das Experiment mit den Ergebnissen (x, y)
wird durch die uniforme Verteilung auf dem
Einheitsquadrat des R2 beschrieben und
die Wahrscheinlichkeit des Ereignisses, dass
der Abstand höchstens t beträgt, ist gleich
der Fläche der Menge At in der nebenstehenden Skizze oder gleich der Fläche des
Einheitsquadrats minus der Flächen der
beiden restlichen Dreiecke, was
P (At ) = 1 − 2
ergibt.
y
1
6
At
t
t
(1 − t)2
= 1 − (1 − t)2 = 2t − t2
2
1
-
x
A19) Berechnen Sie folgende Doppelintegrale:
Z
Z3 πx/2
y
cos
a) I1 =
dydx.
x
x=1 y=0
b) I2 =
Z∞ Z1
u=1 v=−1
c) I3 =
Z1 Zy2
(u − v) · e−u dvdu.
ex/y dxdy.
y=0 x=0
6 Punkte
Lösungen: In den Übungen.
A20) Berechnen Sie folgende Doppelintegrale mit Polarkoordinaten:
ZZ
a) I4 =
(1 + x + y) d(x, y), wobei A = K1 (~0).
A
b) I5 =
ZZ
B
(3 ·
p
x2 + y 2 + 4) d(x, y), wobei B = K3 (~0) \ K1 (~0).
Dabei bezeichne Kr (~0) ⊂ R2 den Kreis um den Nullpunkt mit Radius r.
Lösungen: In den Übungen.
6 Punkte