Experimente zur CP-Verletzung: B

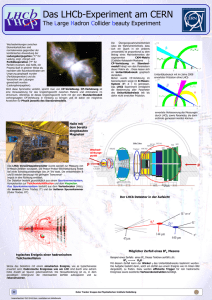
Experimente zur CP-Verletzung: B-Mesonen
Tobias Weber
Die Verletzung der CP-Symmetrie ist seit ihrer Entdeckung
durch J. Cronin, V. Fitch und R. Turlay im System der neutralen K-Mesonen von hohem Interesse für die Teilchenphysik.
Allerdings blieb das K-System lange Zeit das einzige Mesonensystem, in dem die CP-Verletzung nachgewiesen wurde.
Dies änderte sich erst zu Beginn des 21. Jahrhunderts, als die
CP-Verletzung mit hohem experimentellem Aufwand auch bei
den B-Mesonen bestätigt wurde. Die theoretische Erklärung im
Rahmen des Standardmodells wurde von M. Kobayashi und
T. Masukawa mit Hilfe der CKM-Matrix geliefert.
II. T HEORIE
Man unterscheidet 3 verschiedene Klassen der CPVerletzung.
•
•
•
CP-Verletzung im Zerfall (direkte CP-Verletzung)
CP-Verletzung in der Mischung (indirekte CPVerletzung)
CP-Verletzung in der Interferenz zwischen Mischung und
Zerfall
Diese 3 Effekte werden im Folgenden kurz diskutiert werden.
I. E IGENSCHAFTEN DER B-M ESONEN
Die B-Mesonen bestehen aus einem b-Quark oder einem
Anti-b-Quark und leichteren Quarks wie den u,d-Quarks bzw.
deren Antiteilchen. Sie haben eine Masse von ungefähr 5.3
GeV
c2 und können sowohl neutral (in Kombination mit einem
d-Quark) und als geladenen Teilchen (in Kombination mit
einem u-Quark) vorkommen. Ihre Lebensdauer liegt in einer
Größenordnung von 1.6 · 10−12 s.
Zur Erzeugung der B-Mesonen können 2 verschiedene
Prozesse genutzt werden.
• Sie entstehen beim Zerfall der Υ(4S) Resonanz des
Bottoniums bb̄. Diese Resonanz kann zum Beispiel in
Elektron-Positron-Collidern erzeugt werden. Der Vorteil
dieses Verfahrens ist, dass das Υ(4S) fast ausschließlich
in B-Mesonen zerfällt.
• Bei Kollision hoch-energetischer Hadronen können
virtuelle Gluonen entstehen, welche dann in ein BMesonenpaar zerfallen. Diese Methode wird beim LHC
zur Erzeugung von B-Mesonen verwendet werden.
CP-Verletzung im Zerfall
Zur leichteren theoretischen Beschreibung dieses Typs
definiert man zunächst du Zerfallsamplitude Af eines Zustands
M in den Endzustand f als:
Af = hM | H | f i
CP-Verletzung im Zerfall tritt nun auf, wenn verschiedene Zerfallsamplituden zum Zerfall beitragen und die beiden Gesamtamplituden des Zustands und des CP-Zustands verschieden
groß sind, d.h:


 Af 


 Ā  6= 1
f
CP-Verletzung in der Mischung
Analog zu den K-Mesonen kann man unter Zulassung der
CP-Verletzung auch im B-System zwei Superposition aus B 0
0
und B mit verschiedenen Massen definieren:
0
0
| BL i = p | B 0 i + q | B i, | BH i = p | B 0 i − q | B i
Diese beiden Superpositionen können nun zeitlich entwickelt
werden als:
| Bj (t)i =| Bj (0)ie−iMj t e−Γt/2
Abbildung 1.
Die Υ-Resonanzen bei
e+ e− -Kollision
Interessant für die Erforschung der CP-Verletzung wurden
die B-Mesonen 1986, als am ARGUS Detektor in Hamburg
eine Abweichung vom radioaktiven Zerfallsverhalten bei den
B-Mesonen gemessen wurde. Damit war ein weiteres Mesonensystem gefunden in dem CP-Verletzung möglich ist. Wegen
der größeren Masse der b–Quarks sollte diese außerdem
stärker auftreten als bei den K-Mesonen.
Diese Darstellung führt schließlich zu zeitlichen Oszillation
der beiden B-Mesonen untereinander:
1 −Γt
e (1 + cos(∆mt))
2
2
1 q −Γt
0
0
2
| hB | B (t)i | = e (1 − cos(∆mt))
2 p
| hB 0 | B 0 (t)i |2 =
2
Diese Oszillation ist für den Fall pq 6= 1 nicht mehr
symmetrisch was zur indirekten CP-Verletzung führt.
CP-Verletzung in der Interferenz zwischen Mischung und Zerfall
0
Diese Form der CP-Verletzung tritt auf, wenn B 0 und B in
gemeinsame CP-Eigenzustände zerfallen. Hierbei zerfällt der
Zustand M direkt in den Endzustand f, während M zunächst
zu M mischt und dann zerfällt. Zur besseren theoretischen
Beschreibung führt man zunächst die Asymmetrie der Zerfallsbreiten und den Parameter λ wie folgt ein:
λ = ηf
q Af
p Af
0
Af =
Γ(B 0 → f ) − Γ(B → f )
0
Γ(B 0 → f ) + Γ(B → f )
Es lässt sich zeigen, dass es zur CP-Verletzung kommt, wenn
gilt:
q Af
λ = ηf
p Af
Die Größe Af lässt sich dann schreiben als:
Af = −Im(λ) · sin(∆m · t)
III. DAS BA BAR -E XPERIMENT
Zur Zeit gibt es zwei große Experimente, die sich mit der
CP-Verletzung an B-Mesonen beschäftigen. Zum einen das
BaBar-Experiment am SLAC in Kalifornien und Belle am
KEK in Japan. Da beide beide Experimente in Aufbau und
Durchführung sehr ähnlich sind, werden wir uns im Folgenden
dem BaBar-Experiment widmen.
Das BaBar-Experiment ist eine Kolloboration von 500 Physikern und Ingenieuren. Die B-Mesonenpaare werden mit Hilfe
des PEP-II Speicherrings, einem asymmetrischen Collider
für Elektronen und Positronen, über den Zerfall des Υ(4S)
erzeugt, wobei ein verschränkter Zustand aus einem B-Meson
und einem Anti-B-Meson entsteht. Dabei werden die Elektronen auf eine Energie von 9.1 GeV und die Positronen auf eine
Energie von 3 GeV beschleunigt. Dieser Energieunterschied
wird benötigt um den entstehenden Teilchen einen “Boost” im
Laborsystem zu geben und so eine Messung der Wegstrecke
zwischen dem Zerfall der beiden B-Mesonen zu ermöglichen.
Ohne Boost wäre diese Messung nicht möglich, da die Ortsauflösung des Detektors zu gering wäre.
Der Zerfall der beiden B-Mesonen und deren Zerfallsprodukte
werden vom BaBar-Detektor nachgewiesen.
Als Beispiel für diesen Kanal wollen wir uns den Zerfall
B 0 → J/ΨKS beschäftigen, da dieser der geforderte CPEigenzustand ist und CP-Verletzung nur in der Interferenz
auftritt. Mit Hilfe einer Unitaritätsbedingung an die CKMMatrix (vgl. Vortrag V. Gülpers)
∗
Vud Vub
+ Vcd Vcb∗ + Vtd Vtb∗ = 0
und des entsprechenden Unitaritätsdreiecks findet man
Abbildung 3.
Der BaBar-Detektor
Der Detektor setzt sich aus folgenden Komponenten zusammen:
•
•
Abbildung 2.
Unitaritätsdreieck
•
schließlich, unter Beachtung von ηf = −1:
•
V ∗ Vtd
q
= tb ∗ = e2i(π−β)
p
Vtb Vtd
Af = −sin(2β)sin(∆m · t)
Die Untersuchung dieses Zerfalls würde also nicht nur CPVerletzung nachweisen, sondern auch eine Bestimmung des
Winkels β im Unitaritätsdreieck ermöglichen. Somit ist auch
die enge Verbindung der CP-Verletzung zur CKM-Matrix
(indirekt) gezeigt.
•
Ein Silicon Vertex Tracker zur Ortsbestimmung des Zerfalls
Eine Driftkammer zur Teilchenidentifikation über den
charakteristischen Energieverlust
Ein DIRC-Detektor zur Unterscheidung von π- und KMesonen
Ein elektromagnetisches Kalorimeter
Ein 1.5 T Magnet und der IFR zur Rückführung des
Magnetfeldes
Nach der Erzeugung zerfällt nun eines der beiden BMesonen in ein J/Ψ und ein KS . Diese beiden Teilchen
sind ebenfalls instabil und zerfallen schließlich in ihre charakteristischen Zerfallsprodukte. Diese Zerfallsprodukte werden
durch den BaBar-Detektor nachgewiesen und deren Energie
und Impuls bestimmt. Mit diesen Information kann nun ein
B-Meson rekonstruiert werden.
•
•
•
Abbildung 4.
Zerfall eines B-Mesonenpaares
Allerdings ist es noch nicht möglich eine Aussage darüber
0
zu treffen, ob ein B 0 oder B in das J/ΨKS zerfallen ist.
Daher wird eine Information über die Natur des zweiten
B-Mesons benötigt. Diese erhält man durch das sogenannte flavour tagging. Hierbei werden die flavourspezifischen
Zerfälle des zweiten B-Mesons in Elektronen,Myonen bzw.
geladene Kaonen nachgewiesen. Somit sind beide Zerfälle
rekonstruiert.
Nun wird noch die Zeitdifferenz zwischen diesen beiden
Zerfällen benötigt. Diese Information erhält man durch den
Silicon Vertex Tracker, der den Ort der beiden Zerfälle misst.
Dann erhält man die Zeit mit Hilfe des Weg-Zeit-Gesetzes
∆z
.
∆t = βγc
Mit diesen Messwerten kann nun die Asymmetrie der Zerfallsbreiten und damit sin(2β) bestimmt werden.
Abbildung 5.
Messergebnis der Interferenz zwischen Mischung und Zerfall
Man findet: sin(2β) = 0.681 ± 0.025. Also ein klarer
Nachweis der CP-Verletzung im System der B-Mesonen.
AUSBLICK
Für die Zukunft sind weitere Experimente zur CPVerletzung mit K-,B und D-Mesonen geplant. Im Bereich
der B-Meson Forschung ist vor allem das LHCb Experiment
am Large Hadron Collider zu nennen. Durch die höhere
Produktionsrate von B-Mesonen erhofft man sich eine höhere
Genauigkeit der Messungen bzw. mehr Statistik.
L ITERATUR
•
K. Kleinknecht (2003): Uncovering CP-Violation. Experimental Clarification in the neutral K Meson and B Meson
Systems. Springer-Verlag
C. Berger (2006): Elementarteilchenphysik. Von den
Grundlagen zu modernen Experimenten. Springer-Verlag
BaBar Documentation:
http://www.slac.stanford.edu/BFROOT/www/doc/
Vorträge von K. Schubert:
http://hep.phy.tu-dresden.de/~schubert/talks.html