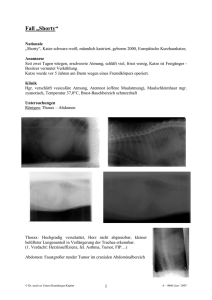
Statik und Dynamik von Flüssigkeiten und Gasen - Physik

Peter Robmann
Physik für
Oberstufenlehrpersonen
Statik und Dynamik von
Flüssigkeiten und Gasen
Physik-Institut der Universität Zürich
Die einzelnen Kapitel in dieser Vorlesung sind Auszüge aus dem Skript “Physik C für BiologInnen
und SekundarlehrerInnen” von Prof. P. Truöl. Ich bedanke mich bei meinem Lehrer und Kollegen
ganz herzlich für das Überlassen seiner Unterlagen.
Inhaltsverzeichnis
A Selbstlernteil Statik und Dynamik von Flüssigkeiten
und Gasen
A.1 Statik und Dynamik der Gase und Flüssigkeiten . . . . .
A.1.1 Hydrostatik . . . . . . . . . . . . . . . . . . . . . . . . . .
A.1.1.1 Beispiel zur Hydrostatik . . . . . . . . . . . . . .
A.1.1.2 Physiologische Anwendungen . . . . . . . . . . .
A.1.2 Dynamik der Flüssigkeiten . . . . . . . . . . . . . . . . .
A.1.3 Grenzﬂächen von Flüssigkeiten – Kohäsion und Adhäsion
iii
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A.1
A.1
A.1
A.2
A.7
A.11
A.30
Abbildungsverzeichnis
A.1 Wasser . . . . . . . . . . . . . . . . . . . . . . .
A.2 Hydrostatischer Druck . . . . . . . . . . . . . .
A.3 Tauchen . . . . . . . . . . . . . . . . . . . . . .
A.4 Blutdruckverteilung im Körper . . . . . . . . .
A.5 Blutdruckmessung . . . . . . . . . . . . . . . .
A.6 Stromlinien . . . . . . . . . . . . . . . . . . . .
A.7 Stromlinien bei einer Verengung der Flussröhre
A.8 Gauss’sche Fläche . . . . . . . . . . . . . . . .
A.9 Füssigkeitsreibung . . . . . . . . . . . . . . . .
A.10 Nicht-Newton’sche Flüssigkeiten . . . . . . . .
A.11 Ohm’sches Gesetz für Rohrsysteme . . . . . . .
A.12 Kirchhoﬀ’sche Kreise für Rohrsysteme . . . . .
A.13 Umströmung eines Flügelproﬁls . . . . . . . . .
A.14 Magnus-Eﬀekt . . . . . . . . . . . . . . . . . .
A.15 Menschlicher Blutkreislauf . . . . . . . . . . . .
A.16 Details zum Blutkreislauf . . . . . . . . . . . .
A.17 Tropfenbildung . . . . . . . . . . . . . . . . . .
A.18 Messung der Oberﬂächenspannung . . . . . . .
A.19 Grenzﬂächen . . . . . . . . . . . . . . . . . . .
A.20 Benetzung . . . . . . . . . . . . . . . . . . . . .
A.21 Kapillarität . . . . . . . . . . . . . . . . . . . .
A.22 Wasserläufer und Waschmittel . . . . . . . . . .
iv
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A.1
A.2
A.8
A.10
A.10
A.12
A.12
A.14
A.17
A.19
A.22
A.22
A.23
A.24
A.26
A.27
A.32
A.32
A.34
A.35
A.36
A.36
Tabellenverzeichnis
A.1
A.2
A.3
A.4
A.5
Blutdruckwerte . . . . .
Viskosität . . . . . . . .
Luftwiderstand . . . . .
Blutkreislauf . . . . . .
Oberﬂächenspannungen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
v
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
A.9
A.17
A.24
A.28
A.33
A
Selbstlernteil Statik und Dynamik von Flüssigkeiten
und Gasen
A.1
A.1.1
Statik und Dynamik der Gase und Flüssigkeiten
Hydrostatik
Gase und Flüssigkeiten sind Systeme, die im strömungsfreien, makroskopischen Gleichgewichtszustand keine Schubspannungen aufweisen (τ = 0). Während bei festen Körpern die Moleküle
durch intermolekulare Kräfte an Gleichgewichtslagen gebunden sind, um die herum sie thermisch angeregte Schwingungen ausführen, beﬁnden sich die Moleküle von Flüssigkeiten und
Gasen in regelloser, ungebundener Bewegung. Ihre mittlere kinetische Energie ist grösser als
die Bindungsenergie. Der Unterschied zwischen Flüssigkeit und Gas beruht auf der Grösse der
intermolekularen Kräfte. In Flüssigkeiten sind die Moleküle dicht gepackt (siehe Abbildung A.1.
Sie bilden Tropfen mit einer deﬁnierten freien Oberﬂäche. Die Kompressibilität ist klein. Gase
dagegen bilden keine Tropfen, sondern beanspruchen das ganze, ihnen zur Verfügung stehende
Volumen. Die Kompressibilität ist im allgemeinen gross.
fest
flüssig
gasförmig
H2O
Abbildung A.1: Die drei Zustandsformen von Wasser.
Der Spannungszustand eines ruhenden Gases oder einer Flüssigkeit ist durch eine einzige Spannung, den hydrostatischen Druck p = p(⃗r), eindeutig bestimmt. Um dies zu verdeutlichen kann
man das in Abbildung A.2 dargestellte Gedankenexperiment machen. In ein mit einer Flüssigkeit
gefülltes Gefäss wird am Ort ⃗r ein kleiner Drucksensor eingebracht. Dieser Drucksensor besteht
aus einem kleinen beweglichen Kolben mit der Fläche dA, der an einer Feder befestigt ist. Aufgrund der äusseren Kraft dF wird er in einem evakuierten Zylinder bewegt. Die Kraft dF bzw.
der Druck p = dF/dA kann aus der Deformation der Feder bestimmt werden. Der Drucksensor
(d. h. die Lage des Flächenelements dA) lässt sich am Ort ⃗r mit einem Mechanismus in jede
beliebige Richtung drehen. Es zeigt sich, dass der Druck p = p(⃗r) unabhängig von der Stellung
des Flächenelements dA ist, d. h. mit anderen Worten, dass der Druck im Gegensatz zur Kraft
eine skalare Grösse ist.
Ist die Substanz frei von irgendwelchen Volumenkräften, insbesondere gewichtslos, so ist der
Druck unabhängig vom Ort. Der Spannungszustand ist homogen. Man nennt dieses Erfahrungsgesetz auch Pascal’s Prinzip, denn der französische Mathematiker, Physiker und Philosoph Blaise Pascal (1623-1662) stellte 1652 fest, dass sich jede Änderung des Drucks, den man auf eine
eingeschlossene Flüssigkeit ausübt, unvermindert auf jeden Teil der Flüssigkeit und die Wände
des Behälters überträgt. Man kann Pascal’s Prinzip mit einem mit Wasser gefüllten Gefäss demonstrieren (Abbildung A.2), an dem ein Zylinder mit verschiebbarem Kolben der Fläche A1
angebracht ist. Drückt man diesen Kolben hinein, so strömt aus allen irgendwo angebrachten
A.1
Drucksensor
dF
dA
F1
x2
Drucksensor
p
p
Druck
p = dF
dA
x1
F2
Abbildung A.2: Links: Gedankenexperiment zum hydrostatischen Spannungszustand; mit einem
Druckmessgerät wird der lokale Druck in der Flüssigkeit gemessen. Rechts: Demonstration von
Pascal’s Prinzip mit einem mit Wasser gefüllten Kolben.
Löchern Wasser mit gleicher Intensität aus. Wenn eine solche Öﬀnung mit einem zweiten Zylinder mit Kolbenﬂäche A2 versehen ist, dann bewegt sich dieser Kolben beim Hereinschieben des
ersten hinaus. Da die Flüssigkeit inkompressibel ist, müssen die Volumenänderungen an den beiden Kolben einander kompensieren. Wenn der erste Kolben um die Distanz x1 hineingeschoben
wird, die Volumenabnahme also x1 A1 beträgt, muss sich der zweite Kolben um x2 herausbewegen, sodass gilt: x2 A2 = x1 A1 . Ausser der Volumenänderung muss noch die geleistete Arbeit an
beiden Kolben die gleiche sein: x2 F2 = x1 F1 . Damit ergibt sich
x1 F1
x2 F2
=
x2 A2
x1 A1
⇒
F2
F1
=
≡p
A2
A1
Der Druck ist der gleiche, wie wir dies postuliert haben.
Die Einheit des Drucks ist das Pascal. Andere gebräuchliche Einheiten sind Atmosphäre (atm),
Torr (zu Ehren von Evangelista Torricelli (1608-1647)) und bar:
1 Pascal = 1 Pa = 1 Newton/m2 = 10−5 bar,
1 atm = 760 Torr = 1.0133 bar = 1.0133×105 Pa, und
1 Torr = Druck einer 1 mm hohen Quecksilber-Säule (Hg) = 133.3 Pa;
zum Vergleich: Druck einer 1 mm hohen Wasser-Säule r (H2 O) = 9.8 Pa.
Die Druckverteilung und der Spannungszustand wird in dem Moment inhomogen, wenn sich
die Flüssigkeit in einem Kraftfeld beﬁndet, wie dies normalerweise der Fall ist. Es treten dann
Druckgradienten auf. Die freie Flüssigkeitsoberﬂäche wird dann zu einer Äquipotentialﬂäche des
Kraftfeldes, wo die potentielle Energie konstant ist und die Kräfte senkrecht zu diesen Flächen
wirken. Im Gravitationsfeld der Erde sind diese Flächen konzentrische Kugeln um den Erdmittelpunkt, im Nahbereich horizontale Ebenen, wie wir das von der Meeresoberﬂäche und der
Oberﬂäche von Seen her kennen. Die Meeresoberﬂäche ist nur dann eine ideale Kugeloberﬂäche,
wenn keine Schubspannungen auftreten, d. h. im statischen Fall. Im dynamischen Fall, z. B. bei
Sturm, muss dies nicht so sein.
A.1.1.1 Beispiele zur Hydrostatik:
In diesem Abschnitt werden ein paar, vorwiegend technische Beispiele aus der Hydrostatik behandelt, oder zum mindestens ihre physikalischen Grundlagen dargelegt.
A.2
Beispiel – hydraulische Presse oder Hebebühne: Man benützt hier die Konstanz des
hydrostatischen Drucks. Der Kolben (K2 ), der
zum Pressen oder zum Heben dient, hat eine grosF2
se Oberﬂäche (A2 ), bewegt sich aber um kleine
Distanzen (x2 ). Der Kolben (K1 ), der hineingeF1
drückt wird, macht grosse Wege, hat eine kleine Oberﬂäche (A1 ) und beansprucht eine kleinere
Kraft (F1 ).
K1 : F1 = pA1
A1
K2 : F2 = pA2
A2
p
A2 >> A1 ⇒ F2 >> F1 , x2 << x1
Beispiel – Druckverteilung in einer vertikalen Flüssigkeitssäule: Die Flüssigkeit beﬁndet sich im Erdfeld, ihre Oberﬂäche ist horizontal, d. h. eine Äquipotentialﬂäche
(mgh = U = const.). Auf die Flüssigkeit (Dichte ρ) drückt
von aussen die Luft mit dem Druck p0 . Bei jedem Volumenelement dV = dxdydz im Innern müssen sich Volumen- und
Oberﬂächenkräfte das Gleichgewicht halten.
Die Volumenkraft ist das Gewicht dG = gdm = gρdV . Die
Oberﬂächenkraft ist gegeben durch das Produkt der Normalspannung (Druck p) mit der Oberﬂäche des Volumenelements (dA = dxdy). Vom Druck wird angenommen, dass er
von der Tiefe (z) abhängt:
p
p0
p(z)
dV
dG
p(z+dz)
z
dG + p(z)dA = p(z + dz)dA ⇒ p(z + dz) − p(z) = ρg
ρ
dxdydz
dA
dp
= ρg
dz
Für eine inkompressible Flüssigkeit ist ρ konstant und wir erhalten durch Integration
dz → 0
⇒
p(z) = p0 + ρgz
Der Druck nimmt mit der Tiefe linear zu, bei Wasser z. B. um circa 1 atm pro 10 m (ρ =
1000 kg/m3 , dp/dz = 9810 Pa/m). Der eingangs erwähnte Unterschied zwischen Gasen und
Flüssigkeiten zeigt sich, wenn man mit den gleichen Ansätzen wie oben die Druckverteilung in
der Luft berechnet.
Beispiel – Druckverteilung in der Atmosphäre: Wir nehmen an, dass die Temperatur in
der ganzen Luftsäule die gleiche ist. Die Dichte der Luft hängt allerdings vom Druck ab. Diese
Abhängigkeit ergibt sich aus der Zustandsgleichung für ideale Gase pV = RT . Diese Gleichung
wird im Teil 2 Thermodynamik, Abschnitt 3.2.1 ausführlich diskutiert. Die Gleichung gibt den
Zusammenhang wieder zwischen dem Druck p, dem Volumen V und der Temperatur T eines
Mols eines idealen Gases, als das wir die Luft bei genügend kleinem Druck ansehen können.
R ist eine Konstante, die ideale Gaskonstante. Man erhält für die Masse eines Mols ρV = M
und damit p/ρ = RT /M = kT /m. m ist die Masse eines Moleküls (M = N0 m), N0 ist die
A.3
Avogadro’sche Zahl und k ist die Boltzmann’sche Konstante (k = R/N0 ). Bei fester Temperatur
ist das Verhältnis von Dichte und Druck konstant.
Die Gleichgewichtsbedingung ist wieder wie oben, nun allerdings mit z positiv nach oben gewählt,
daher das negative Vorzeichen für dp/dz
−
dp
mg
Mg
= ρ(z)g =
p=
p
dz
kT
RT
Wir erkennen wieder eine Gleichung, wo die Änderung einer Grösse (hier eine Abnahme des
Drucks mit der Höhe) proportional zur Grösse (hier Luftdruck) selber ist. Die Lösung der entsprechenden Gleichung ist dann eine Exponentialfunktion (siehe Teil 2 Mechanik, Abschnitt
2.5.4.2.3):
mgz
mgz
p(z) = p0 exp(−
)
⇒ ρ(z) = ρ0 exp(−
)
kT
kT
In dieser sogenannten barometrischen Höhenformel ist p0 der Druck auf der Bezugshöhe (z = 0).
Im Term mgz erkennen wir die potentielle Energie eines Moleküls der Masse m, kT hat daher
ebenfalls die Dimension einer Energie. Für Luft erhält man bei T = 288.15 K (150 C) mit p0 =
1.013 bar und ρ0 = 1.225 kgm−3 folgenden praktischen Ausdruck für die Barometerformel:
p(z) = 1.013 bar · exp(−
z
)
8432 m
Der Luftdruck fällt also in der Höhe
z1/2 = ln 2 · 8432 m = 5844 m
der sog. Halbwertshöhe, auf die Hälfte ab.
Der Exponent (−mgz/kT ) zeigt, dass der Druck für schwere Gase mit der Höhe schneller abnimmt als für leichte Gase. In der folgenden Tabelle sind einige Werte für den Partialdruck von
Sauerstoﬀ (O2 ) und Wasserstoﬀ (H2 ) bei 00 C (273 K) für verschiedene Höhen z zusammengestellt:
Höhe
z (m)
0
1000
5000
10000
Partialdruck von O2
pO2 (z)/pO2 (0)
1.00
0.87
0.50
0.25
Partialdruck von H2
pH2 (z)/pH2 (0)
1.00
0.99
0.96
0.92
Der Partialdruck von O2 fällt bei einer Höhenzunahme um 5000 m auf die Hälfte, der Partialdruck von H2 dagegen nimmt nur um ca. 4 % ab.
Für kleine Höhen z, d.h. für z ≪ p0 /(ρ0 g) ≈ 8000 m, kann die Barometerformel vereinfacht
werden, indem man die Exponentialfunktion entwickelt: exp(−x) ≃ 1 − x für x ≪ 1. Mit
x = ρ0 gz/p0 erhält man
p(z) ≃ p0 − ρ0 gz
Abgesehen vom negativen Vorzeichen (infolge Druckabnahme mit steigender Höhe) ist dieser
Ausdruck identisch mit dem Ausdruck für die Druckverteilung in einer vertikalen Flüssigkeitssäule.
A.4
In der Herleitung der Barometerformel wurde angenommen, dass die Atmosphäre isotherm sei.
Dies ist aber nicht der Fall. Für 1000 m Höhenzunahme sinkt die Temperatur um rund 6.50 C
und erreicht in einer Höhe von 11000 m einen Wert von −560 C. Bis etwa 20000 m bleibt die
Temperatur fast konstant und nimmt anschliessend wieder markant zu. Die Abweichungen des
tatsächlichen Druckverlaufs in der Atmosphäre von demjenigen entsprechend der Barometerformel betragen aber nur einige Prozent, so dass die Barometerformel als eine gute Näherung
betrachtet werden kann.
Auftrieb: Eine Konsequenz der Druckzunahme mit zunehmender Höhe der Wassersäule über
einem eingetauchten Objekt, ist der Auftrieb. Ein starrer Körper erfährt in einer Flüssigkeit
(oder in einem Gas) an seiner Oberﬂäche Druckkräfte, die, wie wir eben gesehen haben, mit der
Tiefe zunehmen. Ihre Resultierende, der sogenannte Auftrieb, ist daher nach oben gerichtet.
Um den Auftrieb zu berechnen, denken wir uns den Körper ersetzt durch die von ihm verdrängte
Flüssigkeit, das sogenannte Déplacement. Da es genau die gleiche Oberﬂäche hat wie der Körper,
erfährt es den gleichen Auftrieb. Da die Flüssigkeit ruht, ist das Déplacement im Gleichgewicht:
∫
⃗
⃗
⃗
⃗
A + GD = 0
⇒
A = −GD = − ρF l ⃗g dV
Der Auftrieb ist entgegengesetzt gleich dem Gewicht der verdrängten Flüssigkeit und greift wie
dieses im Schwerpunkt SD des Déplacements an. Dieses Gesetz ist als Archimedes’sches Prinzip
bekannt.
Auf den eingetauchten Körper beträgt die Gesamtkraft somit
∫
⃗
⃗
⃗
F = A + GK = (−ρF l + ρK )⃗g dV
Ist die Dichte des Körpers grösser als die
der Flüssigkeit, ρK > ρF l , so sinkt er auf
den Grund, ist sie kleiner, ρK < ρF l , so
steigt er solange, bis er teilweise auftaucht.
Weist die Flüssigkeit (oder das Gas) ein
Dichtegefälle auf, ρF l = ρF l (h), so schwebt
der Körper in der Höhe h, wo ρK = ρF l .
A
Wasser
mg
A
Stein
mg
A
Holz
mg
Beispiel – Suspensionen: In einer Flüssigkeit suspendierte Moleküle einer gelösten Substanz
oder Körner irgendeines Stoﬀs mit der Masse ms verhalten sich wie ein verdünntes Gas. (siehe
auch Osmose, Abschnitt 3.3.2 der Thermodynamik). Für die entsprechende Konzentrationsverteilung gilt im Schwerefeld ebenfalls die barometrische Höhenformel:
m′ gz
)
kT
Wegen des Auftriebs ist statt ms die eﬀektive Masse m′ einzusetzen:
∫
′
m = (ρs − ρF l )dV
ρ(z) = ρ0 exp(−
Ist m′ gzmax << kT , so ist die Suspension homogen. Ist m′ gz >> kT , sinken die suspendierten
Körner auf den Grund, für m′ gz < 0 steigen sie zur Oberﬂäche.
Beispiel – Torricelli’sches Ausflusstheorem: Fliesst aus einer Öﬀnung eines Gefässes Flüssigkeit, so hängt die Ausﬂussgeschwindigkeit von der Höhe des Flüssigkeitsspiegels über dem Loch
A.5
ab. Mit abnehmender Höhe nimmt auch die Ausﬂussmenge pro Zeiteinheit ab. In der Zeit dt
strömt die Menge dm = ρAdx = ρAvdt aus dem Loch mit Querschnitt A aus. Ihre kinetische
Energie ist
p0
v2
dT = ρAvdt
2
Diese kinetische Energie ist die Folge der Arbeit dW , die von
den Oberﬂächenkräften geleistet wird, hier von (p − p0 )A.
h
dW = (p − p0 )Adx = (p − p0 )Avdt = dT
v
p0
p
p − p0
ρgh
Mit p − p0 = ρgh ⇒ v = 2
=2
= 2gh
ρ
ρ
2
dV=Adx
Diese Formel hatten wir schon einmal angetroﬀen. Eine von
der Höhe h frei fallendes
√ Objekt erreicht den Boden mit der
Geschwindigkeit v = 2gh.
p0
Bei der sogenannten Mariotte’schen Flasche bleibt die Ausströmgeschwindigkeit konstant
√
v = 2gh′
h'
bis der Flüssigkeitsstand niedriger als h′ ist.
v
p0
Beispiel – Rotierende Flüssigkeit: Wenn ein Zylinder, der mit einer Flüssigkeit der Dichte
ρ gefüllt ist, mit konstanter Winkelgeschwindigkeit ω um seine vertikale Achse rotiert, die Flüssigkeit steigt gegen aussen hoch. Die Oberﬂäche, die, wie wir schon wissen, eine Äquipotentialﬂäche ist, nimmt die Form eines Rotationsparaboloids an. Beﬁnden sich in der Flüssigkeit
gelöste oder eingetauchte Substanzen, so wandern diese, wenn ihre Dichte grösser ist als die
des Wassers, nach aussen und wandern nach innen, auf die Drehachse zu, wenn ihre Dichte
kleiner ist. Dieser Eﬀekt wird in Ultrazentrifugen zur Trennung von Makromolekülen benutzt.
Beide Beobachtungen lassen sich auf die radiale Druckzunahme in der rotierenden Flüssigkeit
zurückführen.
Diese kann aus der Analyse der Kräfte auf ein Volumenelement der Flüssigkeit abgeleitet werden.
In vertikaler Richtung hatten wir vorher gefunden:
dp
= ρg wegen (p(z + dz) − p(z))dA = ρgdzdA
dz
Auf das Volumenelement dV = dzdA wirkt das Gewicht dG = gρdV , das durch den Druckunterschied in vertikaler Richtung (multipliziert mit der Oberfäche dA) aufgehoben werden muss.
In Funktion der Wassertiefe z nahm der Druck linear zu
p(z) = p(z = 0) + ρgz = p0 + ρgz
Rotiert das Volumenelement auf einer Kreisbahn mit Radius r mit Winkelgeschwindigkeit ω,
so ist die Zentripetalbeschleunigung v 2 /r = rω 2 . Die Zentripetalkraft muss von einem radialen
Druckunterschied (multipliziert mit der Oberﬂäche) geliefert werden:
(p(r + dr) − p(r))dA′ = rω 2 dm = rω 2 ρdrdA′ ⇒
A.6
dp
= ρω 2 r
dr
In radialer Richtung ist also die Druckzunahme proportional zum Abstand vom Drehzentrum,
der Druck selber nimmt quadratisch mit dem Radius zu bei festem z
1
1
p(r) = p(r = 0) + ρω 2 r2 = p0 + ρω 2 r2
2
2
Aus den Kräften lassen sich die entsprechenden Kurven der potentiellen Energie und umgekehrt berechnen
r
ω
(siehe Abschnitt 2.6.3)
U (z, r) = ρdV (gz +
ω2 r2
)
2
Für die Oberﬂäche ist U konstant, also
dA
dA'
ω2 r2
gz +
= const.
2
Setzt man für r = 0, z = z0 , so folgt
z = z0 −
dG
ω 2 r2
2g
z0
dZ
p(z)
p(r)
dV
z
dz
p(r+dr)
dr
p(z+dz)
Die Oberﬂäche hat wie behauptet die Form eines Paraboloids. Vergleicht man wieder die vertikale mit der radialen Richtung, so kann auch die Wirkung des sogenannten Zentrifugalauftriebs
erklärt werden nennt. In einer ruhenden Flüssigkeit nimmt der Druck mit der Tiefe zu. Die
resultierende Auftriebskraft zeigt nach oben und hat den gleichen Betrag wie das Gewicht des
Déplacements. In der rotierenden Flüssigkeit nimmt der Druck radial nach aussen zu, die Auftriebskraft zeigt daher nach innen und hat den gleichen Betrag wie die Zentripetalkraft auf das
verdrängte Wasservolumen:
∫
⃗r
⃗
ρF l rω 2 dV
AZ = −
r
Für ρK > ρF l bewegt sich das Objekt K nach aussen, für ρK < ρF l hin zur Drehachse.
Der Zentrifugalauftrieb führt in Zentrifugen zu einer Trennung von Teilchen verschiedener Dichte. Zentrifugen werden in Laboratorien und in technischen Betrieben eingesetzt, z. B. zur Abscheidung von Niederschlägen oder Bakterien, zur Abtrennung der Blutkörperchen vom Serum
oder zur Abtrennung des Fettes von der Milch. Mit sog. Ultrazentrifugen, mit denen man bis zu
20’000 Umdrehungen/s erreicht, ist es gelungen, bei Eiweissmolekülen und anderen makromolekularen Verbindungen den Sedimentationsprozess so detailliert zu verfolgen, dass man das Molekulargewicht und die Molekülform bestimmen konnte. Erfährt ein Mensch bei der Bewegung
auf einer gekrümmten Bahn extreme Normalbeschleunigungen (aN > g, z. B. Akrobatikﬂug,
Raumfahrt), so entsteht ein Druckgefälle im Blut, das je nach Richtung zu einem Über- oder
Unterdruck im Kopf führt.
A.1.1.2
Physiologische Anwendungen
Beispiel – Atmung beim Tauchen: Beim Tauchen muss sich der Druck im Körper (Blut,
Gewebe) dem zunehmenden, äusseren Druck anpassen, damit keine mechanischen Schäden auftreten. Zudem treten beim Tauchen wegen des erhöhten Umgebungsdruckes auf den Körper unter
Wasser Atmungsprobleme auf, welchen mit modernen Tauchgeräten begegnet werden kann.
A.7
Die von der Lunge eingeatmete Luft muss den Druck des umgebenden Wassers haben. Beim Tauchen knapp unter der Wasseroberﬂäche (ca. 40 cm) kann ein Schnorchel zur Atmung verwendet
werden. Die Länge des Schnorchels kann jedoch wegen des Wasserdrucks nicht beliebig lang
gewählt werden: Bei der Atmung kann nur ein Maximaldruck von ca. 11 mbar = 112 cm H2 O
erzeugt werden, so dass das Einatmen mit einem Schnorchel ab ca. 1 m Wassertiefe unmöglich
wird (hypoxämische Anoxie). Für grössere Tiefen (bis ca. 70 m) werden Tauchgeräte verwendet, die den Druck der Einatmungsluft aus einer Druckﬂasche automatisch auf den umgebenden
Wasserdruck einstellen. Damit wird eine Atmung fast wie bei normalen Luftdruckbedingungen
möglich, allerdings mit ein paar unangenehmen und zum Teil gefährlichen Nebenerscheinungen
(siehe Abbildung A.3): Mit zunehmendem Wasserdruck steigt auch der Partialdruck von Stickstoﬀ (N2 ) der eingeatmeten Luft, so dass mehr N2 in Blut und Gewebe aufgenommen wird als
unter Normaldruckbedingungen (in 60 m Tiefe etwa 7 mal mehr als an der Wasseroberﬂäche).
Tauchprofil
zu schnelles
Auftauchen !
Blut
N2
Tiefe (m)
N2 N2-Bläschen
30
3
20
2
10
1
0
N2
0
20
40
Zeit (min)
60
0
Stickstoff-Gewebepartialdruck (bar)
Gasembolie
nach Silbernagel und Despopoulos
Abbildung A.3: Illustrationen zur Atmung beim Tauchen.
Beim Auftauchen wird der Partialdruck von N2 wieder verkleinert und der beim Abtauchen
im Blut und Gewebe gelöste N2 muss wieder abgegeben werden. Beim langsamen und etappenweisen Auftauchen diﬀundiert der zusätzliche N2 in die Atemwege und wird ausgeatmet
(Dekompression). Bei zu raschem Auftauchen entstehen hingegen N2 -Gasbläschen in Blut und
Gewebe. Dies führt zur Depressions- oder Caissonkrankheit. Häuﬁge Symptome sind plötzliche
Bewusstlosigkeit, Krämpfe sowie Lähmungen. Ausserdem wirkt der unter hohem Druck eingeatmete Stickstoﬀ ab Tiefen von mehr als 40 m narkotisch und erzeugt Symptome ähnlich denen
einer Alkoholvergiftung (Tiefenrausch).
Bei Tauchtiefen ab ca. 75 m erreicht der Partialdruck von Sauerstoﬀ (O2 ) Werte, welche eine bedrohliche toxische Wirkung haben. Wird der O2 -Anteil im Gas in der Druckﬂasche nicht
entsprechend verkleinert, so kann zuviel O2 aufgenommen werden; es kommt zu einer SauerstoﬀVergiftung. Im schlimmsten Fall äussert sich eine O2 -Vergiftung in starken Krämpfen und Bewusstlosigkeit, die sogar zum Tod durch Ertrinken führen können.
Beim Tauchen werden gasgefüllte Räume im Körper (z. B. Lunge, Mittelohr) durch den erhöhten
Druck erheblich komprimiert (auf 1/4 des ursprünglichen Volumens in einer Tiefe von 30 m).
A.8
Blutdruck
systolischer Blutdruck
diastolischer Blutdruck
mittlerer Blutdruck
p(mm Hg)
120
80
100
p(mbar)
160
107
133
p(kPa)
16.0
10.7
13.3
Tabelle A.1: Am Oberarm gemessene Blutdruckwerte in den verschiedenen Phasen des Herzzyklus.
Beim Gerätetauchen wird der Druckausgleich zwischen Lunge und Umgebung automatisch hergestellt. Fehlt aber eine Verbindung zwischen Mittelohr und Rachen (z. B. bei Erkältung) kann
der Druckausgleich nicht hergestellt werden, und der Wasserdruck im äusseren Gehörgang kann
das Trommelfell zum Platzen bringen.
Beim Auftauchen dehnen sich diese Gasräume wieder aus. Wird zu schnell, ohne stetiges Luftablassen aufgetaucht, kann es zu einem Lungenriss mit tödlichen Blutungen und Luftembolien
kommen (z. B. rasches Auftauchen aus einem gesunkenen Schiﬀ). Weitere Informationen zu
diesem Thema ﬁndet man in einem Artikel von Moon, Vann und Bennett, Spektrum der Wissenschaft, Oktober 1995.
Beispiel – Blutdruck: Die Gesetze über die Druckverteilung in einer Flüssigkeitssäule gelten
auch für das Blut im Kreislaufsystem des Menschen. Unter dem Blutdruck versteht man den
arteriellen Blutdruck auf Herzhöhe.
Infolge der Herztätigkeit variiert
der Blutdruck bei jedem Herzschlag
Blutdruck (mm Hg)
zwischen einem Maximalwert (syAorta
stolischer Blutdruck) und einem Misystolischer Blutdruck
120
nimalwert (diastolischer Blutdruck)
um den zeitlichen Mittelwert (mittmittlerer Blutdruck
100
lerer Blutdruck). In Ruhe (sitzend
oder liegend) werden normalerweise
80
diastolischer Blutdruck
auf Herzhöhe (gemessen am OberZeit
arm) die in Tabelle A.1 angebenen
Werte beobachtet.
Würde man einem Menschen ein oﬀenes Manometer in die Aorta einsetzen, so würde das Blut
darin auf eine Höhe von ca. 130 cm ansteigen, da 133 mbar ungefähr 130 cm Blutsäule entsprechen (Dichte des Blutes ρB = 1.05 g cm−3 ). Beim aufrechtstehenden Menschen ist der mittlere
arterielle Blutdruck nicht überall gleich: bei einer Körpergrösse von h = 180 cm beträgt der
Druckunterschied zwischen Kopf und Füssen
∆p = ρB gh = 18.5 kPa = 185 mbar.
Der hydrostatische Druck hat grossen Einﬂuss auf den Blutdruck in verschiedenen Körperbereichen (siehe Abbildung A.4).
Die Druckverteilung im Körper hängt daher stark von seiner Lage ab: Erhöhter Blutdruck im
Kopf beim Bücken oder im Kopfstand, ”Blutleere” im Kopf bei raschem Aufstehen, gleicher
Blutdruck im ganzen Körper bei horizontalem Liegen. Daher wird der Blutdruck (sitzend oder
liegend) auf Herzhöhe gemessen. Der Blutdruck kann einfach mit Hilfe der unblutigen Methode
A.9
Blutdruck in verschiedenen Körperbereichen
(Angaben in cm Blutsäule)
(Angaben in mbar)
240
70 cm
60 cm
160
120 cm
200
250 cm
130 cm
Höhe (cm)
80
120
40
71 mbar
133 mbar
256 mbar
0 100 200 300
Blutdruck (mbar)
Abbildung A.4: Illustrationen zur Höhenabhängigkeit des Blutdrucks.
nach Riva-Rocci gemessen werden (siehe Abbildung A.5). Diese Methode wird routinemässig zur
Messung des Blutdrucks im Oberarm auf Herzhöhe verwendet.
Manschette
Druckkammer
P
Pumpe
Abbildung A.5: Blutdruckmessung.
Mit einer kleinen Luftpumpe wird eine Druckkammer aufgeblasen. Durch die um den Oberarm gelegte Manschette wird der von der Pumpe erzeugte Druck auf das deformierbare Gewebe
übertragen. Die Manschette wird soweit aufgeblasen, bis der Manschettendruck, ablesbar an
einem Manometer, grösser ist als der systolische Druck. Dadurch wird der Blutstrom in der
Arterie unterbrochen. Durch Tasten des Pulses (Palpationsmethode) oder durch Abhorchen mit
einem Hörrohr (Stethoskop) in der Ellenbeuge (Auskultationsmethode) kann das Verschwinden
der pulsierenden Strömung festgestellt werden. Nun lässt man die Luft langsam über ein Auslassventil entweichen. Ist der Manschettendruck etwas kleiner als der systolische Druck, beginnt
der Blutstrom wieder. Der Querschnitt ist jedoch noch eingeschränkt, so dass der Blutstrom an
A.10
der verengten Stelle infolge der erhöhten Strömungsgeschwindigkeit turbulent erfolgt (siehe Abschnitt A.1.2). Durch die Wirbelbildung im Blut entstehen charakteristische Geräusche, welche
mit dem Stethoskop hörbar sind. Die Geräusche setzen beim Erreichen des systolischen Drucks
ein. Durch eine weitere Druckerniedrigung in der Manschette wird schliesslich der diastolische
Druck unterschritten und der Strömungsquerschnitt ist wieder völlig oﬀen. Die Turbulenzen und
die damit verbundenen Geräusche verschwinden beim Erreichen des diastolischen Drucks. Die
Angabe des Blutdruckes erfolgt üblicherweise als Kombination des diastolischen und systolischen
Druckes: Im Normalfall beispielsweise 160/100 (angegeben in mbar).
Beispiel – Atmung in grossen Höhen: Die Druckverteilung in der Atmosphäre ist sehr wichtig für die Luft- und Raumfahrtmedizin. Auf Meereshöhe beträgt der Luftdruck pL = 1013 mbar,
der O2 -Partialdruck der Inspirationsluft (pIO2 ) ca. 213 mbar und der O2 -Partialdruck in den AlI
A
veolen (pA
O2 ) rund 133 mbar. Mit zunehmender Höhe nehmen pL , pO2 und pO2 entsprechend
der Barometerformel ab. Sinkt der für die Sauerstoﬀversorgung entscheidende Druck pA
O2 unter
den kritischen Wert von ca. 47 mbar, so kommt es zu Störungen der Gehirnfunktion (Hypoxie).
Bei normaler Atmung ist dieser Grenzwert in einer Höhe von ca. 4000 m erreicht. Durch sogenannte Mehratmung (O2 -Mangelatmung) kann pA
O2 ”künstlich” höher gehalten werden, so dass
eine Atmung ohne technische Hilfsmittel bis ca. 7000 m möglich wird. Grössere Höhen können
nur mit Sauerstoﬀatmung ab Druckﬂaschen erreicht werden. Der O2 -Partialdruck pIO2 ist dabei
fast so gross wie der äussere Luftdruck pL und folglich steigt auch der O2 -Partialdruck pA
O2 in
A
den Alveolen. Mit Sauerstoﬀmasken erreicht pO2 den kritischen Wert ohne Mehratmung bei ca.
12 km Höhe, mit Mehratmung sogar erst bei 14 km. Moderne Verkehrsﬂugzeuge ﬂiegen daher
unterhalb einer Höhe von 14 km, damit bei einem Druckabfall in der Kabine ein Überleben mit
Sauerstoﬀmasken möglich ist. Ein Aufenthalt in Höhen von über 14 km ist auch mit einer Sauerstoﬀmaske nur in einer Druckkabine oder einem Druckanzug möglich (Raumfahrt). Für Höhen
von mehr als 20 km würden ohne diese Schutzvorrichtung die Körperﬂüssigkeiten (z. B. Blut)
zu sieden beginnen, da der Luftdruck unter den Dampfdruck von Wasser bei 370 C absinkt.
A.1.2
Dynamik der Flüssigkeiten
Überlagert sich der statistischen, thermischen Bewegung von Gas- oder Flüssigkeitsmolekülen
eine korrelierte, d. h. geordnete Driftbewegung, so spricht man von einer Strömung. Sie kann
durch ein Stromlinienbild (Abbildung A.6) veranschaulicht werden. Die Stromlinien sind die über
die thermische Bewegung ausgemittelten Bahnen der einzelnen Teilchen oder eines Probekörpers,
der von der Strömung mitgeführt wird. Die Driftgeschwindigkeit ist somit tangential zu den
Stromlinien. Die Geschwindigkeitsvektoren einer Strömung bilden ein Vektorfeld ⃗v (⃗r, t). Die
Stromlinien sind die Feldlinien dieses Feldes.
Ist das Stromlinienbild zeitlich unveränderlich, so spricht man von einer stationären Strömung,
d.h. an einem bestimmten Ort ⃗r ist die Strömungsgeschwindigkeit ⃗v (⃗r) zeitunabhängig. Die Geschwindigkeit eines mit der Strömung mitschwimmenden Teilchens, das ja seinen Ort verändert,
braucht dabei keineswegs zeitlich konstant zu sein. Zeigt eine Strömung ein glattes Stromlinienbild, so nennt man sie laminar. Sind die Stromlinien verwirbelt, so nennt man die Strömung
turbulent. Bei realen Gasen und Flüssigkeiten erfolgt beim Überschreiten einer kritischen Geschwindigkeit vK bei der Um- oder Durchströmung eines Hindernisses ein Übergang von einer
laminaren zu einer turbulenten Strömung. Ursache der Turbulenz sind dynamische Schubspannungen als Folge der Viskosität. Im folgenden wollen wir uns auf laminare Strömungen beA.11
schränken.
v
Stromlinie
P
Abbildung A.6: Bild einer Flüssigkeitströmung um einen Zylinder herum, das mit Einfärbung
der Flüssigkeit sichtbar gemacht wurde (links). Der Geschwindigkeitsvektor der strömenden
Flüssigkeitsmenge ist immer parallel zur Stromlinie (rechts).
A1
v1
A2 v2
Abbildung A.7: Im engen Querschnitt unter der Brücke drängen sich die Stromlinien zusammen
(rechts). Dies bedeutet auch eine höhere Strömungsgeschwindigkeit, solange der Fluss überall
gleich tief ist, und die Oberﬂächenverteilung der Stromlinien den Vorgang beschreibt. Das gleiche
Bild und der gleiche Eﬀekt zeigen sich bei einer Verengung einer Wasserröhre (links).
Kontinuitätsgleichung für stationäre Strömungen: Wird die Anzahl der Stromlinien pro
Flächeneinheit grösser, die Stromdichte, wie wir diese Grösse nennen wollen, grösser, so entspricht dies auch einer grösseren Geschwindigkeit. Abbildung A.6 erinnert an eine uns vermutlich bekannte Beobachtung des Anwachsens der Strömungsgeschwindigkeit in der Nähe einer
Einschnürung des Flussbetts. Die physikalische Grundlage dieser Beobachtung ist die Erhaltung
des Gesamtﬂusses, die einﬂiessende Wassermenge pro Zeiteinheit muss gleich der ausﬂiessenden
sein. Bei kleinerem Querschnitt muss daher die Durchﬂussgeschwindigkeit grösser werden. Die
mathematische Form dieser Erfahrung ist die Kontinuitätsgleichung.
C
Für die mathematische Deﬁnition des Flussbegriﬀes betrachten wir eine sogenannte Stromröhre innerhalb einer stationären Strömung, d. h. einen durch Stromlinien begrenzten
B
Schlauch mit Eintrittsﬂäche A1 und Austrittsﬂäche A2 . In
A2
der Zeit dt ﬂiessen durch A1 und A2 die Wassermengen
A
1
dm1 = ρ1 v1 A1 dt und dm2 = ρ2 v2 A2 dt
A.12
Im stationären Fall muss wegen der Erhaltung der Materie bei A1 gleichviel hinein wie bei A2
hinaus ﬂiessen. Daher gilt die
Kontinuitätsgleichung : ρ1 v1 A1 = ρ2 v2 A2
Bei Flüssigkeiten kann ρ als konstant angenommen werden, ρ = ρ1 = ρ2 , so dass gilt
v1 A 1 = v2 A 2
d. h. der Fluss des ⃗v -Feldes längs einer Stromröhre ist konstant, bzw. der Fluss durch eine
geschlossene Fläche gleich Null. Wir haben hier die Ein- und Austrittsﬂäche senkrecht zur
Strömungsgeschwindigkeit gewählt, was einem Spezialfall entspricht. Für diesen Fall lautet dann
die Aussage der Kontinuitätsgleichung:
Die Geschwindigkeit längs einer stationären, laminaren Strömung ist umgekehrt proportional
zum Rohrquerschnitt.
In etwas allgemeinerer Form deﬁnieren wir als Fluss durch
⃗ ≡ n̂dA)
eine Fläche A (mit dA
∫
∫
∫
∫
⃗
Φ=
⃗v · dA ≡ (⃗v · n̂)dA =
vn dA =
v cos αdA
A
A
A
dA
α
A
n̂
v
Der Einheitsvektor n̂ steht senkrecht auf dem
Flächenelement dA, vn ist die Normalkomponente der
Geschwindigkeit ⃗v .
vcosα= v·dA
dA
Diese Deﬁnition des Begriﬀs Fluss (Φ) schliesst die Möglichkeit ein, dass die Geschwindigkeit
nicht an allen Orten der Fläche A gleich ist und ferner, dass die Fläche nicht notwendigerweise
normal zu den Flusslinien steht. Für A ∥ ⃗v (α = π/2) ist der Fluss minimal, für A ⊥ ⃗v (α = 0)
ist der Fluss maximal. Für eine beliebig gestellte Querschnittsﬂäche A der Stromröhre ist dann
der Fluss Φ konstant.
Diese Deﬁnition des Flusses kann auf beliebige Vektorfelder erweitert werden, anstelle des Ge⃗ das Magnetfeld B,
⃗ oder auch das
schwindigkeitsfeldes ⃗v tritt dann z. B. das elektrische Feld E,
Gravitationsfeld ⃗g .
∫
⃗: Φ≡
Fluss eines Vektorfelds S
∫
⃗ · dA
⃗=
S
A
Sn dA
A
Wählen wir als Fläche, für die wir für das Flussintegral auswerten, eine geschlossene Oberﬂäche
im Raum AV , dann ist der einkommende Fluss gleich dem ausgehenden Fluss, der Gesamtﬂuss
also gleich null, ausser wenn sich im Innern des Volumens V , das von der Oberﬂäche AV begrenzt
wird, eine Quelle beﬁndet.
I
I
⃗ · dA
⃗=
S
Quellenfreies Vektorfeld : Φ =
AV
Sn dA = 0
AV
⃗
Abbildung A.8 zeigt ein Vektorfeld (E−Feld
in diesem Fall), den oberen Teil einer solchen
geschlossenen Oberﬂäche AV (man nennt sie auch eine Gauss’sche Fläche) und einige Flächenelemente auf der Oberﬂäche zur Illustration wie der Fluss zu berechnen ist.
A.13
Gauss'sche Fläche
3
1
2
dA
θ
θ
dA
E
E
E
1
3
dA
2
Abbildung A.8: Eine beliebig geformte geschlossene Oberﬂäche (Gauss’sche Fläche), die in ein
⃗
Vektorfeld (hier das E−Feld)
hineingelegt wird. Drei ausgewählte Flächenelemente sind gezeigt,
die verschiedene Orientierungen des Feldvektors und der Fläche zeigen.
Bernoulli-Gleichung: Wir betrachten wieder die laminare, stationäre Strömung einer inkompressiblen, reibungsfreien und daher idealen Flüssigkeit in einer Röhre variablen
Querschnitts und dazu variabler Höhenlage. Diese Röhre
muss nicht notwendigerweise reell existieren, sondern kann
durch eine Gruppe von zusammengefassten Stromlinien gebildet werden. Die Eintrittsﬂäche A1 und die Austrittsﬂäche A2 sind senkrecht zur Strömung gewählt, und ferner
soll auch die Geschwindigkeit nicht über den Bereich der
Flächen variieren. Gemäss der Kontinuitätsgleichung erhaltem wir für die im Zeitintervall dt die Flächen passierende
Flüssigkeitsmenge dm
L
y
Eingang
v1
p1
y1
Ideale
Flüssigkeit
x
y
Ausgang
v2
p2
y2
x
dm = dm1 = ρv1 A1 dt = dm2 = ρv2 A2 dt
Wir wollen nun eine Energiebilanz aufstellen für den Zeitraum dt. Die vom Druck netto geleistete
Arbeit dW (Druck × Fläche × Weg) ist gleich der Zunahme von kinetischer und potentieller
Energie: dW = dT + dU .
dW = p1 A1 v1 dt − p2 A2 v2 dt
⇒
dT =
p1 − p2 = ρ(
dm 2
(v − v12 )
2 2
dU = gdm(y2 − y1 )
v22 v12
−
+ gy2 − gy1 )
2
2
A.14
ρ
ρ
⇒ p1 + v12 + ρgy1 = p2 + v22 + ρgy2
2
2
Da die Orte 1 und 2 völlig willkürlich gewählt waren, folgt die Konstanz dieses Ausdrucks längs
der ganzen Strömung (y ≡ h):
ρ
p + v 2 + ρgh = const.
2
Bernoulli′ sche Gleichung
Die vom Schweizer Physiker und Mathematiker Daniel Bernoulli (1700-1782) formulierte Beziehung gilt entlang der Stromlinien einer reibungslosen, inkompressiblen Flüssigkeit. Verläuft
die Stromlinie entlang einer Äquipotentialﬂäche der Gravitationskraft, so reduziert sich die Bernoulli’sche Gleichung auf den Ausdruck
ρv 2
+ p = const. ≡ p0
2
p ist der wirkliche, von einem in der Strömung liegenden Manometer gemessene Druck, der Term
ρv 2 /2 hat ebenfalls die Dimension eines Druckes und heisst dynamischer Druck oder Staudruck.
p0 bezeichnet man als den Gesamtdruck. In Worten lautet also die Bernoulli’sche Gleichung:
Statischer Druck (p) plus Staudruck (ρv 2 /2) ergibt den Gesamtdruck (p0 )
Die Bernoulli’sche Gleichung ist die Basis für das Verständnis verschiedener Alltagsphänomene
und technischer Instrumente. Einige von ihnen wollen wir nun näher betrachten.
Beispiel – Messung von Strömungsgeschwindigkeiten mit dem Pitot-Rohr:
v
Beim Pitot-Rohr handelt es sich um einen
B
ρLuft
stromlinienförmigen Hohlkörper, bei dem die
B
Druckdifferenz zwischen dem Staupunkt A
Staupunkt A
vorn und einer seitlichen Öﬀnung B gemessen
wird. In A ist die Strömungsgeschwindigkeit
h
null, bei der seitlichen Öﬀnung dagegen v. Es
ρ
gilt dann (ρA =Dichte der Luft, ρM = Dichte
der Manometerﬂüssigkeit)
A : v = 0, p0 = pA
B : p0 = pB +
ρA 2
v
2
ρA 2
v = ρM gh
2
√
√
2(pA − pB )
2ghρM
v=
=
ρA
ρA
pA − pB =
⇒
Hier haben wir den am Manometer abgelesenen Druckunterschied (Höhe h) bereits eingesetzt.
Beispiel – Hydrodynamisches Paradoxon: Strömt ein Gas
aus einer Druckﬂasche gegen eine bewegliche Platte, so wird diese angesaugt und nicht etwa weggeblasen. Infolge der hohen Geschwindigkeit des Gases zwischen den beiden Platten ist dort der
Druck kleiner als der Luftdruck aussen. Die beiden Platten werden
zusammen gepresst.
A.15
Beispiel: Druckverteilung in einem Venturi-Rohr:
Ein Rohr mit variablem Querschnitt schliesst eine stationäre Strömung ein. Der Druck p im Rohr variiert ebenfalls mit dem Querschnitt. Die Kombination von Kontinuitätsgleichung und Bernoulli’scher Gleichung liefert
v1
A2
=
v2
A1
p1
p2
p3
ρ 2
ρ
ρ
A1
v + p1 = v22 + p2 = v12 ( )2 + p2
2 1
2
2
A2
v
ρ
A2
⇒ p2 = p1 + v12 (1 − 21 ) < p1
2
A2
Mit A1 = A3 folgt p1 = p3 . Im Experiment, ob nun das Rohr
von Luft durchströmt oder von Wasser durchﬂossen wird,
sind die Drucke p2 und p3 kleiner als berechnet. Man beobachtet selbst bei einem Rohr mit unveränderlichen Querschnitt einen linearen Druckabfall. Dies kommt daher, dass
eine der Voraussetzungen der Bernoulli’schen Gleichungen,
nämlich die Absenz von Schubkräften und Reibung nicht
erfüllt ist.
Im Alltag verwendete Varianten des Venturi-Rohrs sind Zerstäuber (a), Wasserstrahlpumpe (b), und Bunsenbrenner
(c). An der Düsenöﬀnung (kleiner Querschnitt) ist die Geschwindigkeit gross, der Druck klein, so dass der Strahl eine
Saugwirkung ausübt. Der erreichbare Enddruck der Wasserstrahlpumpe ist nicht beliebig klein, sondern begrenzt durch
den Dampfdruck pD des Wassers (bei 20◦ C pD = 23 mbar).
Mit Öl- oder Quecksilber-Strahlpumpen bei tiefen Temperaturen können Enddrucke bis zu etwa 10−8 mbar erreicht werden. Beim Bunsenbrenner hilft der Unterdruck in der Nähe
des an der Düse austretenden Gases die für das Aufrechterhalten des Verbrennungsvorgangs notwendige Luft anzusaugen.
p1
p2
v1
p3
v2
v1
Düse
Düse
Luft
Luft
Gas
Zähe Flüssigkeiten: Bei der Einführung der Reibungskräfte im Teil 1 Mechanik, Abschnitt
2.5.3.2.1 haben wir bereits erwähnt und in verschiedenen Beispielen (Kugel im Öl, Schiﬀ) im Teil
1 Mechanik, Abschnitt 2.5.4.2.3 auch benützt, dass reale Flüssigkeiten nicht reibungsfrei sind.
Die Bremswirkung auf sich in der Flüssigkeit bewegende Objekte hing ab von der Zähigkeit
der Flüssigkeit einerseits – charakterisiert durch die Viskositätskonstante η – und der Form
und Beschaﬀenheit der Oberﬂäche andererseits. In einer realen Flüssigkeit treten also Schubspannungen auf, an den Oberﬂächen und im Innern zwischen einzelnen Flüssigkeitsschichten. In
einem Modell, wo man sich die Flüssigkeitsmoleküle durch harte Kugeln ersetzt denkt, wie in
Abbildung A.9 dargestellt, ist diese Reibung dadurch erklärbar, dass beim Gleiten der einzelnen
Schichten übereinander lauter kleine Potentialberge (siehe auch Teil 1 Mechanik, Abbildung
2.46) überwunden werden müssen. Beim Beispiel der rotierenden Füssigkeit im Schwerefeld, das
wir vorher behandelt haben, hätte die Rotation des Gefässes sich ohne Reibung gar nicht auf
die Flüssigkeit übertragen lassen.
A.16
x
2ε
W
Wη
Abbildung A.9: Wenn eine Flüssigkeitsschicht bestehend
aus den die Moleküle darstellenden Kugeln über die darunterliegende gleitet, hat sie Potentialberge der angegebenen Form zu überwinden. Von einer Schicht auf die
nächste wird dabei Impuls übertragen, und daher eine
Kraft ausgeübt. Die Höhe ϵ der Buckel bestimmt die Viskosität η der Flüssigkeit. Um eine Schicht ganz von der
Oberﬂäche abzulösen muss die Energie 2ϵ aufgewendet
werden.
Um den quantitativen Zusammenhang zwischen Reibungskräften
und der Viskosität einer Flüssigkeit zu erhalten, machen wir
einen Modellversuch. Zwischen zwei parallel gestellten Platten,
die sich mit der Geschwindigkeit v0 zueinander bewegen, beﬁndet sich ein Gas oder eine Flüssigkeit. Ist v0 unterhalb einer
kritischen Geschwindigkeit vK , so haften an beiden Platten die
Grenzschichten. Dazwischen stellt sich eine laminare Strömung
mit einer linearen Geschwindigkeitsverteilung v(x) = ax ein. Die
Schubspannungen und Reibungskräfte zwischen den benachbarten
Flüssigkeitsschichten sind, wie dies Newton erstmals formulierte,
proportional zum Geschwindigkeitsgradienten
τ =η
dv
dx
mit
Platte
v
F v
0
Wand
R
d
dv
v0
=a=
dx
d
Das Newton’sche Reibungsgesetz hat die gleiche Form wie die Diﬀusions- und Wärmeleitungsgleichung (siehe Teil 2 Thermodynamik, Abschnitte 3.3.1 und 3.3.2). Bei diesen Prozessen
handelt es sich ebenfalls um Transportphänomene. In der viskosen Flüssigkeit (und auch im
Gas) wird durch die innere Reibung Impuls transportiert. Wärmeleitung kommt durch Energieübertragung und Energietransport zustande, der bei den Stössen der Moleküle untereinander
sowohl in der Flüssigkeit wie im Gas auftritt. Diﬀusion bedeutet Materietransport. Für Gase
steigt, für Flüssigkeiten sinkt η mit zunehmender Temperatur. Für Gase ist η druckunabhängig.
Typische Werte der Viskositätskonstante η sind in Tabelle A.2 aufgeführt. Als Einheit der Viskosität wird normalerweise benützt
1 Poise = 0.1 Nsm−2
Substanz
Luft
H2 O
Rhizinusöl
Glycerin
0◦ C
0.00017
0.0179
17◦ C
Blut
Blutplasma
0.020
η [Poise]
20◦ C
50◦ C
0.00017
0.0101
0.0055
9.50
15.3
23◦ C
30◦ C
0.04
0.0173
0.015
100◦ C
0.00022
0.0028
37◦ C
0.013
A.17
Tabelle A.2: Viskositätskonstante für verschiedene Substanzen
Beispiel – Messung von η: Eine kleine Al-Platte wird durch ein mit Öl gefülltes Gefäss
gezogen. Bei konstanter Kraft, bestimmt durch das Gewicht der an dem Faden hängenden Masse,
lässt sich η aus der Geschwindigkeit der Platte bestimmen. Die Geschwindigkeit nimmt vom
Beginn der Bewegung zunächst exponentiell ansteigend zu (siehe Teil 1 Mechanik, Abschnitt
2.5.4.2.3), und erreicht dann die Grenzgeschwindigkeit, wo sich Antrieb und Reibung die Waage
halten.
Die Gleichgewichtbedingungen lauten
Faden : F − mg = 0
Platte : F − 2Aτ − m′ g = 0
dv
2v0 η
=
dx
d
′
m g ist das um den Auftrieb verminderte Gewicht der Platte, 2Aτ ist – Schubspannung × Fläche – die bremsende Reibungskraft. Es ergibt sich
m′ = d′ A(ρAl − ρÖl )
η=
τ =η
(m − m′ )g d
4A
v0
A
F
Öl
Al
τ
m
G
L
d'
G
d
d'<<d
Übergang zu Turbulenz: Die kritische Geschwindigkeit vK , bei der die laminare Strömung in
eine turbulente umschlägt, hängt auch von der Viskosität η ab, dazu von der Dichte ρ und einer
charakteristischen Länge L (Gefässdimension, Durchmesser des Hindernisses usw.). In unserem
Beispiel wäre L der Plattenabstand. Auf Grund empirischer Resultate ergibt sich
vK = Re
η
ρL
Re ist eine charakteristische Konstante, die dimensionslose Reynold’sche Zahl. Für glatte Rohre
ﬁndet man z. B. Re = 2300. Ist der Rohrdurchmesser L = 1 cm, so erhält man die folgenden
kritischen Geschwindigkeiten:
vK = 23 cm/s f ür Wasser
vK = 320 cm/s f ür Luft
Viele Flüssigkeiten erfüllen das Newtonsche Reibungsgesetz nicht, d. h. die Viskosität η ist
nicht konstant, sondern nimmt mit zunehmendem Geschwindigkeitsgradienten zu oder ab. Solche sogenannten Nicht-Newtonschen Flüssigkeiten sind z. B. Blut, Speichel, Dispersionsfarben,
Pasten, Salben, Gelee. Beispiele für die verschiedenen Flüssigkeiten sind in Abbildung A.10 angegeben. In den thixotropen Substanzen können auch im statischen Zustand (v = 0, dv/dz = 0)
Schubspannungen vorhanden sein, eine Eigenschaft, die im allgemeinen nur festen Körpern zugeschrieben wird. Es zeigt sich hier, dass die Grenze zwischen fest und ﬂüssig nicht scharf ist.
Dies kommt auch darin zum Ausdruck, dass gewisse Stoﬀe gleichzeitig viskoses und elastisches
Verhalten zeigen, d. h. viskoelastisch sind. Bei niedrigen Temperaturen weisen diese Stoﬀe elastische Eigenschaften auf, verlassen jedoch bei höheren Temperaturen den Gültigkeitsbereich
des Hooke’schen Gesetzes und verhalten sich dann wie hochviskose Flüssigkeiten. Viskoelastizität zeigen vornehmlich hochpolymere Substanzen wie Kautschuk und besonders Biopolymere.
Biopolymere dieser Art sind die Proteoglykane, die einen wesentlichen Anteil am Aufbau des
Binde- und Stützgewebes darstellen. Proteoglykane bestimmen die Struktur und Eigenschaften
von Knorpelgewebe. Zusammen mit dem Kollagen und dem Elastin bilden sie ein viskoelastisches
A.18
System. Dank dieser aussergewöhnlichen Eigenschaft kann der Gelenkknorpel bei der Bewegung
unter Druckbelastung grosse Verformungen schadlos ertragen. Mit einer Zerstörung der Struktur
dieser Biopolymere verliert das Knorpelgewebe seine Viskoelastizität und wird instabil.
Blut ist eine besonders komplizierte Flüssigkeit. Es ist eine Suspension von Blutzellen im Blutplasma. Das Blutplasma hat eine relativ hohe Viskosität (siehe Tabelle A.2), es verhält sich
angenähert wie eine Newton’sche Flüssigkeit. Für die Abweichung von einer Newton’schen
Flüssigkeit sind vor allem die roten Blutkörperchen verantwortlich. So ist bei der Polyzythämie
die Anzahl der roten Blutzellen erhöht, was zu einer Zunahme der Viskosität des Blutes ηB
führt. Dies ist auf die Wechselwirkung zwischen den roten Blutkörperchen zurückzuführen. Eine Zunahme der roten Blutkörperchen um 40-50% bewirkt eine Erhöhung von ηB um einen
Faktor 2-3. In diesem Fall muss das Herz seine Leistung erheblich erhöhen, um die gleiche
Strömungsgeschwindigkeit im Kreislauf aufrechtzuerhalten. Im umgekehrten Fall, bei der Anämie,
wird ηB im Vergleich zum Normalwert verringert. Damit der Blutdruck nicht abfällt, muss die
Durchﬂussmenge im Kreislauf entsprechend erhöht werden.
Abbildung A.10: Das Diagramm zeigt die
Abhängigkeit der Schubspannung vom
Geschwindigkeitsgradienten für verschiedene Flüssigkeiten. Der lineare Zusammenhang gilt nur für die Newton’schen
Flüssigkeiten. Die Steigung der Kurve ist
die Viskosität der Flüssigkeit.
Strömung und Geschwindigkeitsverteilung in einem zylindrischen Rohr: In vielen
Anwendungen triﬀt man auf die folgende Situation: Die Strömung einer Flüssigkeit durch ein
zylindrisches Rohr wird durch einen Druckunterschied an den beiden Enden des Rohrs aufrechterhalten. Die alltägliche Erfahrung lehrt, dass die Durchﬂussmenge vom Rohrdurchmesser
einerseits und vom Druck andererseits abhängt. Ferner ist die Geschwindigkeitsverteilung in dem
Rohr inhomogen. In der Mitte ist die Geschwindigkeit am grössten. Beide Befunde ﬁnden wir in
den Hagen-Poiseuille’schen Gesetzen ausgedrückt.
Für ein Rohr mit Radius R der Länge L, in dem durch einen Druckunterschied ∆p eine laminare
Strömung unterhalten wird, ﬁnden wir ein parabolisches Geschwindigkeitsproﬁl
v(r) =
1 ∆p 2
(R − r2 )
4 ηL
A.19
Die Durchﬂussmenge ergibt sich zu
Q=
v
p1
Fp
[m3 s−1 ]
Zum Beweis der beiden Beziehungen denken wir uns aus
der Flüssigkeit eine zylindrische Stromröhre mit Radius r
herausgeschnitten: Infolge des Druckunterschieds ∆p wirkt
auf diesen Zylinder eine Kraft in der Strömungsrichtung
Fp = πr2 (p1 − p2 ) = πr2 ∆p
R
r
π∆p R4
8ηL
Durch das radiale Geschwindigkeitsgefälle dv/dr an der
Mantelﬂäche eine entgegengerichtete Reibungskraft
Fτ = η2πr
dv
dr
Im stationären Fall herrscht Gleichgewicht
v0
dv
F⃗p + F⃗τ = 0 ⇒ πr2 ∆p + 2πrLη
=0
dr
⇒
dv
∆p
r2 ∆p
=−
r Integration : v(r) = −
+C
dr
2ηL
4ηL
p2
Die Integrationskonstante C erhalten wir aus der Randbedingung
v(r = R) = 0 ⇒ C =
R2 ∆
4ηL
Damit ist die erste Beziehung bewiesen.
Die Durchﬂussmenge berechen wir zunächst für einen Hohlzylinder mit gleichem Radius wie die
Stromröhre, aber mit der Wandstärke dr. In diesen Hohlzylinder tritt am Ende im Zeitintervall
t durch die Eintrittsﬂäche 2πrdr das Wasservolumen dV = 2πrdr v(r)t ein.
π∆p(R2 − r2 )
dV
= v(r)2πrdr =
rdr
t
2ηL
Was im gleichen Zeitintervall durch den gesamten Rohrquerschnitt eintritt erhält man durch
Integration:
∫
π∆p R 2
πR4 ∆p
V
=
(R − r2 )rdr =
Q≡
t
2ηL 0
8ηL
Die Wassermenge M ergibt sich aus Q durch Multiplikation mit der Dichte ρ. Bei einer konstanten mittleren Geschwindigkeit v wäre die Durchﬂussmenge Q = πR2 v. Setzen wir die wahre
Durchﬂussmenge Q gleich der mittleren Durchﬂussmenge Q so ergibt sich für die mittlere Geschwindigkeit
R2 ∆p
v=
8ηL
A.20
Damit die Strömung laminar bleibt, muss v < vK gelten. Überschreitet v die kritische Geschwindigkeit, so wird die Strömung turbulent. Bei einer turbulenten Strömung ist die Durchﬂussmenge
kleiner, die Reibung grösser als beim laminaren Fall.
Rohrsysteme – das Ohm’sche Gesetz für Flüssigkeitsströmungen: Für die Auslegung
von Rohrsystemen ist es nützlich das Gesetz von Hagen-Poiseuille etwas umzuformulieren und
den Strömungswiderstand RL einzuführen.
RL =
8ηL
[Nsm−5 ]
πR4
RL nimmt mit der Viskosität des strömenden Mediums linear zu, der Rohrradius geht allerdings
mit der vierten Potenz (RL ∝ 1/R4 ), die Querschnittsﬂäche A quadratisch ein (RL ∝ 1/A2 ).
Mit dieser Deﬁnition erhält man für den Volumendurchﬂuss
Q=
∆p
RL
Diese Form des Hagen-Poiseulle’schen Gesetzes erinnert sehr an das Ohm’sche Gesetz der Elektrizitätslehre
V
I=
RE
V ist hier die elektrische Spannungsdiﬀerenz, RE der elektrische Widerstand, und I der elektrische Strom. Diese formelle Analogie ist in Abbildung A.11 illustriert. Sie kann auf die Berechnung
von Rohrsystemen erweitert werden (Abbildung A.12), für die ähnliche Beziehungen gelten, wie
man sie von elektrischen Stromkreisen her kennt (Kirchhoﬀ ’sche Gesetze, siehe Teil 4 Elektrizität
und Magnetismus, Abschnitt 6.2.2).
In einem elektrischen Stromkreis ist eine Spannungsquelle nötig, z. B. eine Batterie, damit ein
Strom ﬂiesst, in einem Rohrsystem wird der Druckunterschied von einer Pumpe aufrecht erhalten. Schaltet man zwei Rohrsysteme hintereinander, so ergibt sich der gesamte Strömungswiderstand aus der Summe der Einzelwiderstände:
∑
Serie − Schaltung :
RL,tot =
RLi
i
Schaltet man mehrere Röhrensysteme nebeneinander, so erleichtert man den Fluss, und der
gesamte Strömungswiderstand verkleinert sich. Aus der Kontinuitätsgleichung (Flusserhaltung)
ergibt sich:
Q=
∑
i
Qi = ∆p
∑ 1
∆p
=
RLi
RL,tot
Parallel − Schaltung :
i
1
RLtot
=
∑ 1
RLi
i
Will man z. B. N identische parallele Rohre mit Innenradius R durch ein einziges√Rohr der
gleichen Länge mit Innenradius R0 ersetzen will, ergibt sich bei gleichem Fluss R0 = 4 N R. Ein
Rohr von 4 cm Durchmesser kann also 16 Rohre von 2 cm Durchmesser ersetzen.
Das Stokes’sche Reibungsgesetz: Für die Reibungskraft, die auf ein sich in einer Flüssigkeit
bewegendes Objekt wirkt, hatten wir gefunden
Rv ∝ v
⃗ v = −β⃗v
R
z. B. Kugel : β = 6πηr
A.21
Rohrwiderstand RL
elektrischer Widerstand RE
Q
I
Q= 1 ∆p
RL
I= 1 V
RE
∆p
V
V
∆p
R
R
ρW
η
I
Q
L
L
Geschwindigkeitsprofil
R
R
v
Rohr
v
elektrischer Leiter
Abbildung A.11: Äquivalente Grössen für Flüssigkeitsströmungen (links) und elektrische Ströme
(rechts).
Pumpe
Spannungsquelle
- +
V
ţp
RE2
RL2
RL5
RL3
RL1
RE5
RL4
RE3
RE1
RE4
RL6
RE6
RL7
RE7
Abbildung A.12: Äquivalenz zwischen einem geschlossenem Rohrsystem (links) und einem elektrischen Stromkreis (rechts).
A.22
Die gleiche Abhängigkeit ergibt sich für die Kraft Rv , die die strömende Füssigkeit auf die
Rohrwand ausübt.
Rv = 2πRLτ (r = R) = πR2 ∆p = 8πηLv
d. h. die viskose Reibung ist für Newton’sche Flüssigkeiten in der Tat proportional zu v, wie wir
dies angenommen hatten.
Weitere Kräfte in Strömungen – Dynamischer Auftrieb und Widerstand: Wird ein
Körper von einem Gas oder einer Flüssigkeit umströmt, so treten neben den schon behandelten
auch Kräfte auf, die proportional dem Quadrat der Anströmgeschwindigkeit sind.
Von einem Stromlinienbild, wie z. B. dem für ein Flügelproﬁl in Abbildung A.13, kann die Geschwindigkeitsverteilung (Kontinuitätsgleichung) und damit die Druckverteilung (Bernoulli’sche
Gleichung) der umströmenden Substanz abgelesen werden. Der aufgerichtete Flügel lenkt den
Luftstrom nach unten ab. Das Ablenken entspricht einer Kraft des Flügels auf den Luftstrom,
und nach dem 3. Newton’schen Prinzip übt der Luftstrom eine entgegengesetzt gleiche Kraft
auf den Flügel aus. Die vertikale Komponente (allgemeiner die Komponente normal zu ⃗v ) dieser
⃗ D , die horizontale Komponente (allgemeiner die
Kraft nennt man den dynamischen Auftrieb A
⃗ D . Da die Dichte der
Komponente parallel zu ⃗v ) nennt man den dynamischen Widerstand R
Stromlinien oberhalb des Flügels grösser ist als unterhalb, ist die Geschwindigkeit dort höher,
der Druck kleiner und die resultierende Kraft daher aufwärts gerichtet, wie es uns die Bernoulli’sche Gleichung lehrt. Der dynamische Auftrieb hat nichts mit dem statischen Auftrieb in
Gasen und Flüssigkeiten zu tun, auf den das Prinzip von Archimedes hinweist und der Ballone
ﬂiegen und Eisberge schwimmen lässt. Der dynamische Auftrieb entsteht nur, wenn Strömung
und umströmtes Objekt relativ zueinander in Bewegung sind.
Luftwiderstand
Auftrieb
v2
Anstellwinkel
v1
Abbildung A.13: Stromlinienverteilung für
einen Flugzeugﬂügel der gegenüber der Horizontalen leicht geneigt ist. Die resultierende Kraft hat eine vertikale Komponente
(dynamischer Auftrieb) und eine horizontale Komponente (dynamischer Widerstand).
In einer reibungsfreien Flüssigkeit wäre der dynamische Widerstand null, mit Reibung haben
wir eine Stoke’sche Reibungskraft proportional zur Geschwindigkeit. Diese Kraft genügt jedoch
nicht, um den dynamischen Widerstand zu erklären, der mit dem Quadrat der Geschwindigkeit
zunimmt.
RD = CR v 2
Die Ursache dieser Kraft ist die Wirbelbildung hinter dem umströmten Hindernis, d. h. diese
Kraft tritt erst dann auf, wenn der Übergang von der laminaren zur turbulenten Strömung
(v > vK ) schon vollzogen ist. Die sich an den Grenzﬂächen bildenden Wirbel tragen kinetische
Energie mit, die dem Flugobjekt entzogen wird. Der Koeﬃzient CR hängt sehr stark von der
Geometrie des Proﬁls ab. Welche Geometrie die günstigste ist lehrt uns die Natur, für einen
“stromlinienförmigen” Hai ist CR sicher kleiner als für einen Kugelﬁsch. In Tabelle A.3 sind die
Werte für verschiedene ﬂächengleiche Proﬁle miteinander verglichen.
A.23
Der dynamische Auftrieb macht sich auch bemerkbar bei der Bewegung von rotierenden Objekten. Ein rotierendes Objekt hat eine andere Flugbahn als ein Objekt, das sich nicht dreht.
Abbildung A.14 demonstriert die Ursache dieser Beobachtung, die man den Magnus-Eﬀekt nennt.
Der rotierende Ball nimmt die Luft an seiner Oberﬂäche mit, und erzeugt dadurch eine asymmetrische Geschwindigkeitsverteilung und eine entsprechende Kraft, die je nach Drehrichtung nach
unten gerichtet (top-spin, kürzere Flugbahn), noch oben gerichtet (bottom spin im Golf, slice
im Tennis, längere Flugbahn) oder, häuﬁg unerwünscht, wenn die Drehung nicht um eine horizontale Achse erfolgt, seitwärts gerichtet ist. In diesem Fall bekommt man in der horizontalen
Projektion gekrümmte Flugbahn.
v2
v1
Abbildung A.14: Die Stromlinienverteilung
für einen sich nicht drehenden Ball (oben)
ist symmetrisch bezüglich einer horizontalen
Achse. Für einen sich drehenden Ball führt
die Zähigkeit des Mediums zu einer Zirkulationsströmung um den Ball herum (Mitte).
Der anströmende Luftstrom wird durch die
Zirkulation abgelenkt und die entsprechende
Kraft ist für diese Drehrichtung aufwärts gerichtet (unten).
Luftwiderstand
F
Auftrieb
v1
v2
Widerstandskoeffizient CR
0.22
0.34
0.08
1.58
1.33
Tabelle A.3: Vergleich verschiedener ﬂächengleicher Proﬁle.
Blutkreislauf: Die folgende Diskussion ist dem Skript der Vorlesung Physik für Mediziner
entnommen. Bei der physikalischen Beschreibung des Blutkreislaufsystems können die Gesetze
aus Hydrostatik und Hydrodynamik angewendet werden. Allerdings muss man sich über einige
Einschränkungen im klaren sein. Das Blut ist, wie bereits betont wurde, keine Newton’sche
Flüssigkeit. Die Blutkörperchen geben Anlass zu komplizierten Strömungsverhältnissen in den
Blutgefässen, welche sich vor allem in den feinen Kapillaren bemerkbar machen. Ferner muss
berücksichtigt werden, dass die Arterien und Venen elastisch (keine starren Röhren) sind und
der Blutdruck im Kreislaufsystem örtlich und zeitlich variiert. Trotzdem können wir im Rahmen
A.24
der erarbeiteten Kenntnisse eine vereinfachte Betrachtung des Blutkreislaufsystems durchführen,
welche die wesentlichen Zusammenhänge recht gut beschreibt.
Wie äussert sich der nicht-Newton’sche Charakter des Bluts ? Blut besteht aus festen Bestandteilen mit verschiedenen Formen, die im Blutplasma suspendiert sind. Die roten Blutkörperchen
z. B. sind scheibenförmig. Bei kleinen Geschwindigkeiten sind sie zufällig orientiert, bei grossen
Geschwindigkeiten jedoch richten sie sich aus, um das Fliessen des Blutes zu erleichtern. Daher
nimmt die Viskosität von Blut ab, wenn die Strömungsgeschwindigkeit zunimmt.
Wie das nebenstehende Volumendurchﬂuss-Druckdifferenz-Diagramm für Blut
zeigt, ist die Viskosität und damit
der Volumendurchﬂuss vom Anteil der
Blutkörperchen (Hämatokrit) abhängig.
Q
50% Hämatokrit
20% Hämatokrit
∆p
Bei kleinen Druckdiﬀerenzen verhält sich Blut durchaus wie eine Newton’sche Flüssigkeit (gestrichelte Gerade in der Abbildung), aber bei höheren Druckdiﬀerenzen treten abhängig vom
Hämatokrit Abweichungen auf. Das Gesetz von Hagen-Poiseuille ist dann streng genommen
nicht mehr gültig. Es ist aber immer noch eine gute Näherung.
Das menschliche und tierische Herz-Kreislaufsystem (siehe Abbildung A.15) ist geschlossener
Stromkreis, bei dem das Herz als Pumpe das Druckgefälle aufrecht erhält. Der Druckunterschied
∆p bewirkt im Ruhezustand einen Blutﬂuss von circa 4–5 ℓ/min (Herzminutenvolumen). Durch
die periodische Pumptätigkeit des Herzens wird das Blut schubweise mit einer Frequenz von etwa
60 Herzschlägen pro Minute in die Aorta gepresst. Dabei variiert im gesunden Ruhezustand der
Blutdruck in der Aorta zwischen einem Maximalwert (systolischer Blutdruck) von circa 160 mbar
und einem Minimalwert (diastolischer Blutdruck) von circa 100 mbar (siehe Abschnitt A.1.1.2
und Abbildung A.16).
Durch die Pumptätigkeit des Herzens wird dem Blut kinetische Energie erteilt, welche durch zwei
Mechanismen im Kreislaufsystem dissipiert wird, nämlich durch Ausdehnung und Kontraktion
der Aorta (elastisches Gefäss) und durch innere Reibung des Blutes in den Gefässen. Wegen
der Dissipation werden die Blutdruckschwankungen in der Aorta und in den Arterien geglättet
und der mittlere Blutdruck im Kreislaufsystem nimmt zunehmend ab (Abbildung A.16). Der
Druckabfall in einem Blutgefäss kann mit Hilfe des Gesetzes von Hagen-Poiseuille abgeschätzt
werden. In Tabelle A.4 sind einige Angaben für die verschiedenen Abschnitte (Abbildung A.16)
des Blutkreislaufsystems zusammengestellt. Mit den Werten aus dieser Tabelle ergibt sich für
die Aorta mit einem Volumenstrom von QAorta = 7 · 10−5 m3 s−1 (= 4.2 l/min) und η = 5 ·
10−3 Nsm−3 ein Druckabfall von nur 0.36 mbar. Zum Vergleich wollen wir den Druckabfall im
Bereich der Arteriolen abschätzen. Unter der vereinfachten Annahme einer Parallelschaltung
von N Arteriolen ist der Volumenstrom durch eine einzige Arteriole QArteriole = QAorta /N ≃
2 · 10−12 m3 s−1 . In den Arteriolen verhält sich Blut nicht mehr wie eine Newton’sche Flüssigkeit.
Infolge der Ausrichtung der Blutkörperchen nimmt die Viskosität η ab. Mit einem geschätzten
Wert von η ≃ 3 · 10−3 Nsm−3 , QArteriole ≃ 2 · 10−12 m3 s−1 und den tabellierten Werten für R und
L erhält man für den Druckabfall im Bereich der Arteriolen ∆p ≃ 30 mbar. Dieser Wert ist 100
mal grösser als ∆p in der Aorta. Die Gesamtquerschnittsﬂäche im Kreislaufsystem nimmt mit
verfeinerter Verzweigung zu. Die Querschnittsﬂäche der herznahen Aorta ist etwa 3 cm2 und die
mittlere Strömungsgeschwindigkeit ist dort rund 30 cm/s. Der Gesamtquerschnitt der Kapillaren
beträgt hingegen etwa 1500 cm2 und die Strömungsgeschwindigkeit gemäss der Kontinuitätsgleichung v = 30 cm/s·(3 cm2 /1500 cm2 ) ≈ 0.06 cm/s. Diese Verlangsamung des Blutstromes
A.25
Gehirn
Gehirnkappilaren
Armaterie
Armvene
Lungenarterie
Aorta
Lungenvene
linker Vorhof
linke Herzkammer
obere Hohlvene
Lunge
rechter Vorhof
rechte Herzkammer
untere Hohlvene
Leber
Milz
Niere
Pfortader
Dünndarm
Beinvene
Beinarterie
Schematische Darstellung des Blutkreislaufsystems
rechte Vorkammer
Atrium
Vena cava
linke Vorkammer
Ventrikel
Herz
Venen
Venolen
Aorta
Arterien
Kapillaren
Arteriolen
Hochdrucksystem
Organe
Niederdrucksystem
Abbildung A.15: Der menschliche Blutkreislauf (oben, schematisch) und das dazugehörige physikalische Modellsystem (unten).
A.26
Blutdruck (mbar)
Verlauf des Blutdruckes im Kreislaufsystem
160
Systolischer Druck
Diastolischer Druck
80
0
Pumpe
Aorta Arteriole
Kapillare venöser Abschnitt
präkapillare
Verzweigungen
Arteriolen
Venolen
grosse
Arterien
Arterienäste
Aorta
Kapillaren
grosse Venen
Venenäste
Vv. cavae
Abbildung A.16: Verlauf
des Blutdrucks (oben)
in
den
verschiedenen
Abschnitten des Kreislaufsystems (unten).
ist notwendig für einen eﬀektiven Stoﬀaustausch.
Treten bei diesen Strömungsgeschwindigkeiten Turbulenzen auf ? Rechnen wir für Blut mit
der Dichte ρ = 103 kg/m3 und der Viskosität η = 4 · 10−3 Nsm−2 , so ergibt sich mit einer
Reynold’schen Zahl von 2300 (für glatte Rohre) eine kritische Geschwindigkeit vk von 0.46
m/s für die Aorta und von 1100 m/s für die Kapillaren. Die Strömung in den Kapillargefässen
ist daher laminar. In der Aorta hingegen kann die Strömungsgeschwindigkeit des Blutes unter
Umständen 1 ms−1 erreichen und die Strömung turbulent werden. Im allgemeinen kommt es dazu
nur bei krankhaften Verengungen der Aorta. Auch eine zu hohe Dosierung eines den Blutdruck
erhöhenden Medikaments kann eine turbulente Strömung in der Verengung bewirken, wodurch
der Strömungswiderstand massiv ansteigt und der Volumendurchﬂuss sinkt anstatt zu steigen.
Unter der Annahme, dass alle Gefässe eines Kreislaufabschnittes identischen Querschnitt haben und parallel geschaltet sind, kann man die prozentualen Anteile der verschiedenen Bereiche am Strömungswiderstand (RLeﬀ /RLtot ) abschätzen (siehe Tabelle A.4). Mehr als 90% des
gesamten Strömungswiderstandes ﬁnden wir im Arterien-Kapillaren-System, wobei die Arteriolen (40%) und die Kapillaren (30%) den grössten Anteil ausmachen. Trotz der enorm grossen
Gesamtquerschnittsﬂäche stellen diese feinen Gefässe den Hauptwiderstand im Kreislaufsystem
dar, da ihre Einzelwiderstände quadratisch von ihrem Querschnitt abhängen. Lediglich 7% des
Strömungswiderstandes entfallen auf den venösen Bereich mit niedrigem Blutdruck. Beim stehenden Menschen in Ruhe reicht der niedrige Blutdruck fast nicht aus, um das venöse Blut von
den Füssen zurück ins Herz zu leiten. Als Folge davon sammelt sich Blut in den Venen der Beine
an und erhöht den Druck in den Kapillaren, was ein Anschwellen der Beine bewirken kann. Beim
Gehen hingegen wird durch die Kontraktion der Muskeln in den Waden der Rückﬂuss des Blutes
begünstigt.
A.27
Gefäss
Aorta
Grosse Arterie
Arterie
Arteriole
Kapillare
Venole
Vene
R (m)
1 · 10−2
2 · 10−3
5 · 10−4
1 · 10−5
4 · 10−6
1.5 · 10−5
1 · 10−3
N
1
40
2000
4 · 107
5 · 109
8 · 107
1200
A (m2 )
3 · 10−4
6 · 10−4
1.5 · 10−3
1.3 · 10−2
1.5 · 10−1
6 · 10−2
4 · 10−3
L (m)
0.4
0.2
0.05
0.002
0.001
0.002
0.05
v (m/s)
0.3
0.15
0.06
0.007
0.0006
0.0015
0.02
RLeﬀ /RLtot (%)
25
40
28
7
Tabelle A.4: Zusammenstellung geometrischer Daten (Radius R, Anzahl Gefässe N , Gesamtquerschnittsﬂäche A, Länge L), der Strömungsgeschwindigkeit v und des Anteils am Gesamtwiderstand RLeﬀ /RLtot für die verschiedenen Abschnitte des Blutkreislaufs.
Bei starker körperlicher Anstrengung steigt der Volumenstrom des Blutes im Kreislaufsystem
an. Dies wird erreicht durch ein Ansteigen des Blutdruckes, durch gesteigerte Herztätigkeit (Frequenzerhöhung) und durch eine gesteuerte Dehnung/Kontraktion der Gefässe (besonders in den
Arteriolen). Nach dem Gesetz von Hagen-Poiseuille wird durch eine Vergrösserung (Verkleinerung) des Gefässradius von 20% der Volumendurchﬂuss um (mehr als) den Faktor 2 vergrössert
(reduziert). Bereits bei geringen, krankhaften Gefässverengungen kann deshalb nur mit einer
dauernden Mehrbelastung des Herzens ein konstanter Blutﬂuss gewährleistet werden.
Damit der Blutkreislauf aufrechterhalten werden kann, muss das Herz dauernd Arbeit leisten.
Die Pumpleistung P des Herzens lässt sich auf einfache Weise grob abschätzen. Die Leistung
einer Pumpe ist
P = F · v = ∆p · A · v
F = ∆p · A (Druckunterschied ∆p × Querschnittsﬂäche A) ist die von der Pumpe ausgeübte
mittlere Kraft und v die mittlere Geschwindigkeit der Flüssigkeit. Die Grösse Q = A · v ist der
Volumendurchﬂuss, so dass sich für die Leistung des Herzens die einfache Beziehung ergibt
Leistung des Herzens :
P = Q∆p
Mit Hilfe dieser Beziehung kann die mittlere Leistung P im sogenannten grossen Kreislauf berechnet werden. Der mittlere Blutdruck des Menschen ist ∆p ≃ 133 mbar = 1.33 · 104 Nm−2
und der mittlere Volumendurchﬂuss Q ≃ 1 · 10−4 m3 s−1 . Mit diesen Werten erhält man für die
mittlere Leistung des Herzens: P = ∆p · Q ≃ 1.3 Watt. Bei starker körperlicher Anstrengung
wird P um einen Faktor 5 erhöht. Im Lungenkreislauf beträgt die mittlere Leistung des Herzens
nur ungefähr 0.2 Watt, da der Blutdruck am Ausgang des rechten Ventrikels circa 6 mal kleiner
ist als in der Aorta. Es ist bemerkenswert, dass die Leistung des Herzens nur circa 2% (1.5 Watt)
des sog. Grundumsatzes (ca. 80 Watt) im ganzen Organismus ausmacht.
A.28
Zusammenfassung: Hydrostatik und -dynamik
Hydrostatischer Druck: Der Spannungszustand einer Flüssigkeit ist durch eine einzige Spannung, den hydrostatischen Druck p [Pascal] charakterisiert. Flüssigleitsoberﬂächen sind
Äquipotentialﬂächen. In einer vertikalen Flüssigkeitssäule variiert der Druck p mit der
Tiefe z wie
p(z) = p0 + ρgz
In der isothermen Atmosphäre nimmt der Partialdruck eines Gases mit der Höhe z ab
p(z) = p0 exp(−
mgz
)
kT
Auftrieb: Ein in eine Flüssigkeit oder ein Gas (Dichte ρF ) eingetauchter Körper (Dichte ρK )
⃗ die sich aus dem Gewicht
erfährt eine seinem Gewicht entgegengesetzte Auftriebskraft A,
⃗
GD der verdrängten Gas- oder Flüssigkeitsmenge berechnen lässt
∫
⃗ = −G
⃗D = −
ρF ⃗g dV
A
VK
Strömungen: Eine Strömung ist charakterisiert durch das Vektorfeld ⃗v (r,⃗ t), die Strömungsgeschwindigkeit.
Stationäre Strömung: ⃗v = ⃗v (⃗r); laminare Strömung: glatte Feldlinien (Stromlinien), v <
vk = kritische Geschwindigkeit; turbulente Strömung: verwirbelte Stromlinien, v > vk .
In einer stationären Stromröhre einer inkompressiblen Flüssigkeit mit Eintrittsﬂäche dAi
und Austrittsﬂäche dAa gilt wegen der Flusserhaltung die
Kontinuitätsgleichung
vn ⊥ dA
vni dAi = vna dAa
Es gilt ferner die Bernoulli − Gleichung
ρ
p + v 2 + ρgh = p0 = const
2
Der Term ρv 2 /2 wird dynamischer Druck genannt.
Zähe Flüssigkeiten − innere Reibung: Tritt in einer Flüssigkeit ein Geschwindigkeitsgradient dv/dx auf, so wirken zwischen den Flüssigkeitsschichten Reibungskräfte (dynamische
Schubspannungen τ ), die gegeben sind durch das
Newton′ sche Reibungsgesetz
τ =η
dv
dx
Der Koeﬃzient η wird Viskosität genannt [Nsm−2 ] = [10 Poise].
vk = Re
η
ρD
Re = Reynold′ sche Zahl, D = Rohrdurchmesser
A.29
Zusammenfassung: Hydrodynamik
Zähe Flüssigkeiten − Rohrsysteme: Für eine Flüssigkeitsströmung in einem zylindrischen
Rohr der Länge L mit Radius R und Druckunterschied ∆p zwischen den Enden ergibt sich
eine radiale Geschwindigkeitsverteilung
v(r) =
∆p 2
(R − r2 )
4ηL
Für die Durchﬂussmenge pro Zeiteinheit (Volumenﬂuss) Q gilt das
Gesetz von Hagen − Poiseuille
Q=
π∆p 4 ∆p
R =
8ηL
RL
8ηL
Strömungswiderstand
πR4
Für zusammengesetzte Rohrsysteme mit Strömungswiderständen RLi gelten die Kirchhoﬀ’sche Maschenregeln wie für elektrische Stromkreise, d. h.
∑
∑
−1
−1
Serieschaltung RL,tot =
RLi
Parallelschaltung RL,tot
=
RLi
RL =
i
i
Dynamischer Auftrieb und Widerstand: Auf ein umströmtes Proﬁl (Anströmgeschwindig⃗ D ⊥ ⃗v0 (Bernoulli) und bei genügend hohen
keit ⃗v0 ) wirken der dynamische Auftrieb A
⃗ D ∥ ⃗v0 :
Geschwindigkeiten (Turbulenz, Wirbelablösung) der dynamische Widerstand R
AD = CA v02
RD = CR v02
Die Konstanten CA und CR hängen von der Proﬁlform und dem Anstellwinkel ab. Der
dynamische Auftrieb führt bei rotierenden Flugkörpern zu Veränderungen der Flugbahn
(Magnus-Eﬀekt).
A.1.3
Grenzflächen von Flüssigkeiten – Kohäsion und Adhäsion
Unter Kohäsionskräften verstehen wir die inneren, intermolekularen Kräfte in einer Substanz,
welchen wir schon öfters begegnet sind. Der abstossende Anteil wirkt nur zwischen benachbarten Molekülen. Die Reichweite der anziehenden
Kraft wirkt sich über mehrere Moleküle hinweg
aus, über Distanzen von ca. 10−8 m. Im Innern
einer Flüssigkeit ist ein Molekül den anziehenden Kräften benachbarter Moleküle von allen
Seiten ausgesetzt. Die resultierende Kraft F⃗tot
ist null. Anders liegen die Verhältnisse für ein
Molekül nahe der Oberﬂäche. Hier ergibt sich
eine in das Innere der Flüssigkeit gerichtete resultierende Kraft F⃗tot .
A.30
~ 1nm
Ftot
Ftot = 0
Die nach innen gerichteten, intermolekularen Kräfte ziehen die Flüssigkeit zusammen und erzeugen somit in der Flüssigkeit einen Binnendruck pi , dessen Grösse von den Molekularkräften
abhängt. Die Stärke des Binnendruckes kann für feste Körper und Flüssigkeiten aus Zugversuchen bestimmt werden. Fehlstellen im Kristallaufbau, in Flüssigkeiten vor allem gelöste Gase, welche bei niedrigen Drucken Blasen bilden, erschweren jedoch die Messungen, so dass die
experimentell gefundenen Werte nur untere Grenzen darstellen. Für Wasser beträgt der Binnendruck pi ≈ 104 bar = 109 Pa und für feste Körper liegen die höchsten Messwerte bei
pi ≈ 2 · 105 bar = 2 · 1010 Pa. Für Gase und Flüssigkeiten kann auch aus dem Term a/V 2
in der Van der Waals’schen Zustandsgleichung für reale Gase (siehe Teil 2 Thermodynamik,
Abschnitt 3.2.2)
a
(p + 2 )(V − b) = RT
V
der zusätzliche Druck abgeschätzt werden, der im Innern durch die intermolekularen Kräfte
entsteht. Die Konstante b gibt das minimale Volumen an, den ein reales Gas bei dichtester
Packung der Moleküle einnehmen kann. Der Term a/V 2 entspricht gerade dem Kohäsionsdruck,
denn auch ohne äusseren Druck p zieht sich das Gas wie unter dem Druck a/V 2 stehend zusammen. Bei Normalbedingungen (Molvolumen VM = 22400 cm3 , (i)) und im ﬂüssigen Zustand
(V = b, (ii)) ergibt sich für He und Wasser
He : (i) 7 × 10−5 atm, (ii) 60 atm
H2 O : (ii) 6000 atm
Adhäsionskräfte heissen die intermolekularen Kräfte, wenn sie zwischen Molekülen verschiedener
Substanzen, also vor allem an Grenzﬂächen auftreten. Je nach Art der beteiligten Moleküle kann
die Adhäsion (A) grösser oder kleiner sein als die entsprechende Kohäsion (K).
A > K: Zwei Flüssigkeiten vermischen sich. Eine Flüssigkeit benetzt einen festen Körper. (Experiment: Essig – Wasser)
A < K: Zwei Flüssigkeiten entmischen sich. Keine Benetzung eines festen Körpers durch eine
Flüssigkeit. (Experiment: Paraﬃnöl – Wasser)
Durchmischung zweier Flüssigkeiten
Entmischung zweier Flüssigkeiten
Grenzfläche
A>K
A>K
Oberflächenspannung: Grenzt eine Flüssigkeit an Vakuum so treten keine Adhäsionskräfte auf. Wenn keine anderen äusseren Kräfte vorhanden sind, so bewirkt die Kohäsion, dass
alle Molekülabstände möglichst klein werden, d. h. die Flüssigkeit wird Kugelform annehmen
(Regentropfen, Hg-Tropfen, Experiment: schwebende Olivenölkugel in einer Alkohol-WasserMischung, siehe Abbildung A.17). Eine Energiebetrachtung führt zum gleichen Resultat. Jede
Bindung an ein Nachbarmolekül liefert einen negativen Beitrag (−EB ) zur potentiellen Energie.
A.31
Diese ist daher kleiner, je mehr solcher Bindungen vorhanden sind. Den Oberﬂächenmolekülen
fehlen jedoch nach aussen die Nachbarn, d. h. es fehlen Bindungen. Die gesamte Energie ist
daher minimal, wenn möglichst wenige Moleküle an der Oberﬂäche sitzen, d. h. das Verhältnis
von Oberﬂäche zu Volumen minimal ist, was wieder zur Kugelform führt:
√
A
3
4.84
4 3
3 4π
= =3
= √
Kugel : V = πr , A = 4πr2 ⇒
3
3
V
r
3V
V
A
6
6
4.84
Würfel : V = a3 , A = 6a2 ⇒
= = √
> √
3
3
V
a
V
V
Flüssigkeitstropfen (unstabil)
Flüssigkeitstropfen (stabil)
Oberfläche
Flüssigkeit
Abbildung A.17: Illustration zur Tropfenbildung bei Flüssigkeiten.
Will man die Oberﬂäche vergrössern, so muss man Energie in die Flüssigkeit hineinstecken. Dies
lässt sich mit einem Drahtbügel, der in eine Seifenlösung eingetaucht wird und dabei eine Lamelle aufspannt, quantitativ zeigen (Abbildung A.18). Der Bügel hängt an einer Waage, die ohne
Lamelle einen kleineren Ausschlag zeigt. Die Oberﬂäche wird um den Betrag dA = 2Ldx vergrössert. Die Kraft F ergibt sich aus der Diﬀerenz der Anzeigen mit und ohne Lamelle. Die beim
Herausziehen des Bügel geleistete Arbeit ist dW = 2F dx. Das Verhältnis der hineingesteckten
Energie (geleisteten Arbeit) zur Oberﬂächenvergrösserung nennt man Oberﬂächenspannung γ.
Es gilt:
[
] [
]
2F dx
F
dE
Energie
Kraft
dW
=
=
γ=
=
dA
2Ldx
L
dA
Fläche
Länge
L
F=Gm
Lamelle
F=Gm
dx
F
F
F
Abbildung A.18: Messung der Oberﬂächenspannung.
Grenzt die Flüssigkeit nicht an Vakuum, sondern an ein anderes Medium, so gelten die obigen
Überlegungen wenigstens näherungsweise, wenn dieses sehr verdünnt ist, wie z. B. ein Gas.
A.32
Substanz
Wasser
Seifenlösung
C2 H5 OH (Alkohol)
Hg (Quecksilber)
Öl
Äthyl-Äther
Temperatur [◦ C]
18
20
20
15
20
20
γ [N/m]
0.073
0.030
0.0223
0.407
0.032
0.017
Tabelle A.5: Oberﬂächenspannungen für verschiedene Flüssigkeiten
Typische Werte für γ an Flüssigkeitsoberﬂächen, über welchen sich Luft beﬁndet, sind in Tabelle
A.5 aufgeführt. Die Oberfächenspannung ist temperaturabhängig. Sie kann z. B. für Wasser
durch sogenannte Detergentien stark verringert werden.
An ebenen Oberﬂächen ist die Resultierende der Oberﬂächenspannung gleich Null. Auf ein konvexes Flächenelement
dagegen resultiert eine Kraft nach innen, auf ein konkaves
eine solche nach aussen. In beiden Fällen strebt die gestörte
Oberﬂäche zur ebenen, minimalen Form zurück.
Eine Seifenblase zieht sich zusammen, bis im Gleichgewicht
der innere Überdruck gleich dem Druck der Oberﬂächenspannung ist. Wir können wieder die für die Vergrösserung
des Blasenradius und damit der Oberﬂäche notwendige Arbeit berechnen (es sind innere und äussere Fläche der Blasenhaut zu berücksichtigen !):
padA
pidA
pi
r → r + dr ⇒ dA = 16πrdr, dV = 4πr2 dr
dW = ∆p dV = γdA ⇒ ∆p = pi − pa =
4γ
r
Der Überdruck ist umso grösser, je kleiner der Radius der
Seifenblase ist. Gleich grosse kommunizierende Seifenblasen
sind daher miteinander im labilen Gleichgewicht. Sobald die
eine etwas kleiner ist als die andere, schrumpft sie solange,
bis die verbleibende Kalotte denselben Krümmungsradius
hat wie die grosse Blase.
Die Flächen minimaler Energie müssen nicht notwendigerweise Kugelﬂächen sein. Betrachten wir eine beliebig gekrümmte, gespannte Oberﬂäche in der Nähe eines Punktes P . Ihre Krümmung kann durch zwei Krümmungsradien
in zwei zueinander senkrechten Koordinatenrichtungen gekennzeichnet werden. Bei einer Lamelle gilt:
∆p = 2γ(
1
1
+
)
R1 R2
A.33
r1
R1
R2
R2
R2
R1
Wenn R1 = R2 = r gilt ﬁnden wir wieder das Resultat der Seifenblase. Eine von zwei Kanten
begrenzte, oﬀene Lamelle hat auf beiden Seiten denselben Druck, d. h. ∆p = 0 Diese Bedingung
kann erfüllt werden, wenn die Lamelle eben ist (R1 = R2 = ∞) oder eine sogenannte Sattelﬂäche
(R1 = −R2 ). Die Diﬀerentialgeometrie zeigt, dass solche Fälle tatsächlich Minimalﬂächen sind.
Grenzflächenspannung: Beﬁndet sich ausserhalb der Flüssigkeit (1) nicht ein Gas, sondern
eine andere Substanz (2), so zeigt die resultierende Kraft auf ein Molekül von (1) ins Innere von
(1), wenn die Kohäsionskräfte innerhalb von (1) grösser sind als die Adhäsionskräfte von (2) auf
(1) (Abbildung A.19). Es gelten die obigen Beziehungen, wobei statt γ die Grenzﬂächenspannung
γ12 einzusetzen ist. Wenn die Adhäsion grösser als die Kohäsion ist, nimmt γ12 negative Werte
an (→ maximale Grenzﬂäche).
2
Α
γ2
Luft
γ1
1
Flüssigkeit
1
Κ
Flüssigkeit
2
γ12
Abbildung A.19: Adhäsion und Kohäsion an Grenzﬂächen. Links: Flussigkeit (1) und andere
Substanz (2) (Flüssigkeit oder Festkörper). Rechts: Flüssigkeit (1) und Gas (2).
Grenzt eine Flüssigkeit (1) an eine zweite (2) und an Luft, so treten drei Grenzﬂächenspannungen auf: γ12 , γ1 und γ2 . γ1 , γ2 (> 0) sind gleich der oben behandelten Oberﬂächenspannung,
solange die Adhäsion zwischen Flüssigkeit und Gas vernachlässigt werden kann (Abbildung
A.19). Im Gleichgewicht muss die Vektorsumme der drei Spannungen gleich Null sein. Ist dies
nicht möglich, wie z. B. bei einem Ölﬁlm auf Wasser (γ12 = 0.018 < γ1 − γ2 = 0.073 − 0.032
[N/m]), so breitet sich das Öl auf dem Wasser zu einer monomolekularen Schicht aus. Auf diesem
Eﬀekt beruht die Wirkung von Detergentien. Da auch sie sich in sehr dünnen Schichten an der
Wasseroberﬂäche ausbreiten, genügen schon ganz geringe Mengen, um die Oberﬂächenspannung
erheblich zu reduzieren.
Auch an festen Körpern (K) existieren Oberﬂächenspannungen und Oberﬂächenenergien. Sie
spielen z. B. bei der Rissbildung eine wichtige Rolle. Die Grenzﬂächenenergien Festkörper–Gas
(K − G) sind jedoch meistens sehr klein, da sich an der Festkörperoberﬂäche eine adsorbierte Gasschicht bildet (γkG ≈ 0). Grenzt in einem Behälter Flüssigkeit (F ), an eine Wand (K)
und an Luft (G) so beinﬂussen die Grenzﬂächenspannungen die Oberﬂächenform (siehe Abbildung A.20). Die Oberﬂäche des festen Körpers ist unbeweglich und es gilt γKG ≈ 0. Für die
Kraftkomponenten parallel zu dieser Fläche ergibt sich im Gleichgewicht
γF G ≈ γF
γKF + γF cos ϕ ≈ 0 ⇒ cos ϕ =
−γKF
γF
Für γKF > 0 ist π/2 ≤ ϕ ≤ π und die Wand wird nicht benetzt (z. B. Quecksilber). Für γKF < 0
ist 0 < ϕ ≤ π/2 und die Wand wird benetzt (z. B. Alkohol). Ist |γKF | > γF , so existiert keine
Lösung, die Flüssigkeit breitet sich über die ganze Fläche aus, sie benetzt vollständig.
A.34
nicht benetzende Flüssigkeit
benetzende Flüssigkeit
γF
γKF > 0
φ
φ γF
γKF > 0
φ > π/2
Glas-Wasser
φ > π/2
Glas-Quecksilber
Tropfenbildung auf Glas
Wasser
φ> π
2
Quecksilber
φ> π
2
φ
φ
Glas
Abbildung A.20: Illustration zu den Grenzﬂächenspannungen und Oberﬂächenformen bei benetzenden und nicht benetzenden Flüssigkeiten.
Kapillarität: Infolge der Grenzﬂächenspannung wirkt längs der Gefässwand auf die Berandung
einer Flüssigkeit eine Kraft pro Länge
γKF = −γF cosϕ
In einem runden Rohr wird die Flüssigkeit hinuntergedrückt (kapillare Depression) oder hochgezogen (kapillare Attraktion), bis Gleichgewicht herrscht mit dem Gewicht der Flüssigkeitsäule
(siehe Abbildung A.21).
2πrγF cos ϕ = ρghπr2
Die Steighöhe ergibt sich daraus zu (mit cos ϕ = 1 für vollständige Benetzung)
h=
2γF cos ϕ
2γF
(=
)
ρgr
ρgr
Die Steighöhe bei Benetzung (Adhäsion > Kohäsion) ist umgekehrt proportional zum Radius und tritt daher vor allem bei dünnen Rohren (Kapillaren) in Erscheinung. Benetzung oder
Nicht-Benetzung von festen Körpern durch Wasser und die damit verknüpften anziehenden und
abstossenden Kräfte spielen in der Natur eine wichtige Rolle, z. B. bei Ausbreitung von Wasser im Humus, in Pﬂanzenkapillaren, bei der Fortbewegung von Amöben, beim Fettgeﬁeder
von Wasservögeln und auch bei Insekten, die auf dem Wasser laufen. Auch Wasch- und Imprägniermittel, Kugelschreiber, Wattetampons usw. nützen Kapillarwirkungen aus. Abbildung
A.22 illustriert die letzteren beiden Beispiele.
A.35
Fγ
2r
h
φ
h
φ
Kapillare Attraktion
Kapillare Depression
Abbildung A.21: Illustration zur kapillaren Attraktion (links) und Depression (rechts).
Gewebe mit Wasserschicht
Wasser
Wasser
nicht imprägniert
imprägniert
Wasser geht durch
Wasser geht nicht durch
Gewebe
Abbildung A.22: Unten links: Kapillarwirkung beim Wasserläufer. Oben: Einﬂuss eines
Imprägniermittels auf die Wasserdurchlässigkeit von Gewebe.
A.36
pa > p i
pa
Beﬁndet sich zwischen zwei Platten ein Flüssigkeitstropfen,
so werden sie dadurch angezogen oder abgestossen, je nachdem ob die Flüssigkeit benetzt oder nicht. Benetzt sie, so
wirkt, wie oben, die Kapillarkraft nach aussen. Im Innern
entsteht ein Unterdruck, der eine Anziehung der Platten bewirkt. Benetzt sie nicht, so drückt die resultierende Kapillarkraft nach innen, der Überdruck im Innern erzeugt eine
Abstossung der Platten.
pi
pa
pa
ppii
pa
pi > pa
Zusammenfassung: Kräfte an Grenzflächen
Kohäsion, Adhäsion: Die anziehenden Kräfte zwischen den Molekülen innerhalb einer Substanz werden unter dem Begriﬀ Kohäsion zusammengefasst, diejenigen zwischen verschiedenen Molekülen einer Mischung oder an den Grenzﬂächen zweier verschiedener Substanzen als Adhäsion.
Kohäsionsdruck in einem realen Gas (Van der Waals’sche Zustandsgleichung):
(p + pK )(V − b) = RT
pK =
a
V2
Kohäsionsdruck in einer Flüssigkeit:
pK =
A>K
Durchmischung, Benetzung
a
b2
A<K
Entmischung, keine Benetzung
Kohäsionskräfte in einer Flüssigkeit führen zur Oberﬂächenspannung γ, deﬁniert als die
zur Vergrösserung einer Oberﬂäche dA notwendige Energie dE:
γ=
dE
dA
[N/m]
Beispiele: Seifenblase mit Radius R
∆p = pinnen − paussen =
4γ
R
Flüssigkeitslamelle mit Krümmungsradien R1 , R2
∆p = pi − pa = γ(
1
1
+
)
R1 R2
Adhäsionskräfte an den Grenzﬂächen einer Flüssigkeit mit einem Festkörper führen zum
Kapillareﬀekt, A < K kapillare Depression, A > K kapillare Attraktion.
A.37