Lösungen Lösungen - Ernst Klett Verlag

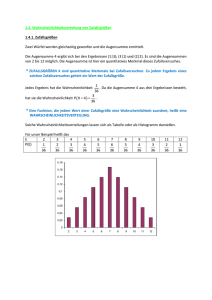
Lösungen
Lösungen
Bemerkung zur Schreibweise
Beachte, dass die Wahrscheinlichkeit eines Ergebnis­
ses oder eines Ereignisses als Bruch, Dezimalbruch
oder in Prozentschreibweise angegeben werden kann.
Pinboard – Zufall und Wahrscheinlichkeit
1
a) P (Zahl 1 zweimal) = }
1 ≈ 0,0278 = 2,78 %
36
b) P (Zahl 1 mindestens einmal) = }
11 ≈ 0,3056 36
= 30,56 %
c) P (Zahl 1 genau einmal) = }
10 ≈ 0,277 8 = 27,78 %
36
25
d) P (keine 1) = }
36 ≈ 0,6944 = 69,44 %
e) P (erst die Zahl 1, dann die Zahl 3) = }
1 ≈ 0,0278 36
= 2,78 %
f) P (Zahl 4 mindestens einmal) = }
0 = 0
36
• e
ine Herzkarte zu ziehen: H 7, H 8, H 9, H 10, HB, HD, HK, HA P (Herzkarte) = }
8 = }4 1 = 0,25 = 25 %
32
• e
ine schwarze Karte zu ziehen: P 7, P 8, P 9, P 10, PB, PD, PK, PA Kr 7, Kr 8, Kr 9, Kr 10, KrB, KrD, KrK, KrA 16
P (schwarze Karte) = }
= }2 1 = 0,5 = 50 %
32
• e
in Bild zu ziehen: KaB, KaD, KaK, HB, HD, HK, PB, PD, PK, KrB, KrD, KrK 12 3
}
P (Bildkarte) = _
32 = 8 = 0,375 = 37,5 %
• e
in rotes Ass zu ziehen: KaA, HA P (rotes Ass) = }
2 = }
1 = 0,0625 = 6,25 %
32
16
b) Die günstigen Ergebnisse und die Wahrscheinlichkeit für das Ereignis, mit zwei Würfeln
• e
ine Augensumme größer als sechs zu werfen: Eine Tabelle, in der die Augensumme aufgeführt ist, hilft, die günstigen Ergebnisse für diese und die nächsten Teilaufgaben zu finden.
2 (1 + 2 + 2 VP)
Bei dieser Aufgabe muss man sich entscheiden, ob
man die Wahrscheinlichkeit für die einzelnen Ereig­
nisse in Bruchschreibweise, Dezimalbruchschreib­
weise oder Prozentschreibweise angibt.
a) Die Wahrscheinlichkeiten für die drei Ereignisse gelbes Feld, rotes Feld oder grünes Feld sind bekannt.
P (Gelb) = 40 % = 0,4 = }25 P (Rot) = }4 1 = 0,25 = 25 %
P (Grün) = 30 % = 0,3 = }
3 10
a) Da alle vier Ergebnisse zusammen das sichere Ereignis mit der Wahrscheinlichkeit 1 = 100 % darstellen, gilt:
P (Blau) + P (Gelb) + P (Rot) + P (Grün) = 1
p (Blau) = 1 – (P (Gelb) + P (Rot) + P (Grün) ( )
= 1 – 2 }5 + }4 1 + }
3 = 1 – }
10 = }
1 10
20
20
1
2
3
4
5
6
Alternative – rechnen mit Dezimalbrüchen:
P (Blau) = 1 – (0,4 + 0,25 + 0,3) = 1 – 0,95 = 0,05
Alternative – rechnen mit Prozenten:
P (Blau) = 100 % – (10 % + 25 % + 30 %)
= 100 % – 95 % = 5 %
1
2
3
4
5
6
7
b) P (Gelb oder Blau) = P (Gelb) + P (Blau) P (Augensumme kleiner als 6) = }
10 ≈ 0,2778 = 27,78 %
36
2
3
4
5
6
7
8
3
4
5
6
7
8
9
= 2}5 + }
3 + }
1 = }
10
20
20
4
5
6
7
8
9
10
c) P (nicht Rot) = P (Gelb) + P (Grün) + P (Blau) 3
5
6
7
8
9
10
11
6
7
8
9
10
11
12
= 2}5 + }
3 + }
1 = 3}4 10
20
Alternative
1 3
P (nicht Rot) = 1 – P (Rot) = 1 ­ 4_ = 4_
2
P (1) = }
4 ≈ 0,3077 = 30,77 %
13
P (2) = P (3) = P (4) = P (5) = }
2 ≈ 0,1538 = 15,38 %
13
P (6) = }
1 ≈ 0,0769 = 7,96 % 13
38
Erwartungswert = }
13 ≈ 2,923
Klassenarbeit 2.1
1 (3 + 3 VP)
Wir bezeichnen Karo mit Ka, Herz mit H, Pik mit P
und Kreuz mit Kr. Die Bilder Bube, Dame, König mit
B, D, K und das Ass mit A.
Von jeder Farbe gibt es acht Karten (7, 8, 9, 10, Bube,
Dame, König, Ass). Somit besteht ein Skatspiel aus
4 · 8 = 32 Karten.
a) Die günstigen Ergebnisse und die Wahrscheinlichkeit für das Ereignis, aus einem Skatspiel
42 ( 1; 6), (2; 6), (3; 6), (4; 6), (5; 6), (6; 6), (2; 5), (3; 5), (4; 5), (5; 5), (6; 5), (3; 4), (4; 4), (5; 4), (6; 4), (4; 3), (5; 3), (6; 3), (5; 2), (6; 3), (6; 1) P (Augensumme größer als 6) = }
21 = }
7 ≈ 0,5833 12
36
= 58,33 %
• e
ine durch drei teilbare Augensumme zu werfen: (1; 2), (1; 5), (2; 1), (2; 4), (3; 3), (3; 6), (4; 2), (4; 5), (5; 1), (5; 4), (6; 3), (6; 6) P (Augensumme durch drei teilbar) = }
12 = }3 1 36
≈ 0, 3333 = 33, 33 %
• einen Pasch zu werfen: (1; 1), (2; 2), (3; 3), (4; 4), (5; 5), (6; 6) 6
P (Pasch) = }
= }6 1 ≈ 0, 1667 = 16, 67 %
36
• zwei aufeinander folgende Zahlen zu werfen: (1; 2), (2; 3), (3; 4), (4; 5), (5; 6) P (zwei aufeinander folgende Zahlen) = }
5 36
≈ 0,1389 = 13,89 %
2 Zufall und Wahrscheinlichkeit
© Ernst Klett Verlag GmbH, Stuttgart 2010 | www.klett.de | Alle Rechte vorbehalten Diese Probeseiten ermöglichen Ihnen eine konkrete inhaltliche Auseinandersetzung mit dem neuen Lehrwerk. Die hier dargestellten Texte, Bilder und
Illustrationen sind gezielt für bestimmte Lernsituationen und passgenau zu den Inhalten der Lehrpläne ausgesucht und verstärken die Lerneffekte. Die
methodische Abstimmung der Texte einerseits und Bilder andererseits wird durch diese Probeseiten verdeutlicht
c) Die günstigen Ergebnisse sind
(2; 1), (2; 4), (4; 1), (4; 4), (6; 1), (6; 4), (8; 1), (8; 4)
P (erst gerade Zahl, dann Quadratzahl) = }
8 = }8 1 64
= 0,125 = 12,5 %
d) Zahlen größer als drei und kleiner als sieben: 4; 5; 6
Die günstigen Ergebnisse sind:
(4; 4), (4; 5), (4; 6)
(5; 4), (5; 5), (5; 6)
(6; 4), (6; 5), (6; 6)
P (zweimal eine Zahl, die größer als drei und kleiner 9
als sieben ist) = }
= 0,140 625 ≈ 14,06 %
64
4 (2 + 3 VP)
Werden die Kugeln mit einem Griff gezogen, so entspricht dies dem Zufallsversuch „Ziehen ohne Zurücklegen, ohne Berücksichtigung der Reihenfolge“. a) Ein Baumdiagramm hilft, die Lösung zu finden.
9
3 (2 + 2 + 2 + 2 VP)
Die acht Sektoren des Glücksrades sind gleich groß. Daher sind die Wahrscheinlichkeiten für das Auftreten der Ziffern 1 bis 8 bei jeder Drehung gleich.
P (1) = P (2) = P (3) = P (4) = P (5) = P (6) = P (7) = P (8)
= }81 Das Glücksrad wird zweimal gedreht. Insgesamt gibt es 8 × 8 = 64 mögliche Ergebnisse. Die Wahrscheinlichkeit für ein mögliches Ergebnis ist demnach }
1 .
64
a) Die Zahlen 1 und 4 sind Quadratzahlen. Die günstigen Ergebnisse sind (1, 1), (1, 4), (4, 1) und (4, 4)
P (zwei Quadratzahlen) = }
4 = }
1 = 0,0625 64
16
= 6,25 %
b) Die günstigen Ergebnisse sind (1; 1), (1; 3), (1; 5), (1; 7), (3; 1), (3; 3), (3; 5), (3; 7), (5; 1), (5; 3), (5; 5), (5; 7), (7; 1), (7; 3), (7; 5), (7; 7)
16
P (zweimal eine ungerade Zahl) = }
= }4 1 = 0,25 64
= 25 %
Nach der Summenregel gilt:
P (zwei Kugeln gleicher Farbe) = }3 1 P (zwei Kugeln ungleicher Farbe) = }3 1 + }3 1 = }23 b) Es muss noch eine rote Kugel hinzugefügt werden. Das Baumdiagramm macht dies deutlich.
P (zwei Kugeln gleicher Farbe) = }2 1 P (zwei Kugeln ungleicher Farbe) = }4 1 + }4 1 = }2 1 2 Zufall und Wahrscheinlichkeit Probeseite aus: Schnittpunkt 9 Nordrhein-Westfalen, Training Klassenarbeiten
ISBN 978-3-12-740490-6
43
3