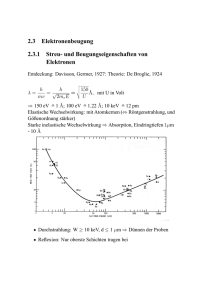
Mathematik I Mathematik I
Werbung

Mathematik Mathematik II Dr. Dr.Marc-A. Marc-A.Zschiegner Zschiegner © Dr. Zschiegner 2008 Seite 1 Kapitel 1: Grundlagen Organisation Organisation Termin: Termin: Donnerstags, Donnerstags,8.00 8.00––9.30, 9.30,9.50 9.50––11. 11.20 20 Raum Raum407 407 Leitung: Leitung: Dr. Dr.Marc-A. Marc-A.Zschiegner, Zschiegner,Dipl.-Math., Dipl.-Math.,StR. StR. [email protected] [email protected] Tel.: Tel.:0641 0641//99-32083 99-32083 © Dr. Zschiegner 2008 Seite 2 Kapitel 1: Grundlagen Seite Was Wasist istMathematik? Mathematik?––Der DerInhalt Inhalt •• Geometrie Geometrie(seit (seitEuklid, Euklid,ca. ca.300 300v.v.Chr.) Chr.) Die Lehre vom uns umgebenden Raum Die Lehre vom uns umgebenden Raum(2D, (2D,3D, 3D,...) ...) •• Algebra Algebra(seit (seitder derAntike) Antike) Zahlen und Rechnen Zahlen und Rechnen •• Analysis Analysis(seit (seitdem dem18.Jahrhundert) 18.Jahrhundert) Die Lehre vom Unendlichkleinen Die Lehre vom Unendlichkleinenund undden denGrenzübergängen Grenzübergängen •• Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung(20. (20.Jahrhundert) Jahrhundert) (Wie) können wir den Zufall verstehen? (Wie) können wir den Zufall verstehen? © Dr. Zschiegner 2008 Seite 3 Kapitel 1: Grundlagen Was Was ist ist Mathematik? Mathematik? ––Die DieMethode Methode •• Definitionen Definitionen Festlegungen Festlegungenvon vonBegriffen. Begriffen. In der Mathematik In der Mathematikwissen wissenwir wirganz ganzgenau, genau,worüber worüberwir wirreden. reden. •• Sätze Sätze Aussagen. Aussagen.Die DieErkenntnisse Erkenntnisseder derMathematik. Mathematik. •• Beweise Beweise In Inder derMathematik Mathematikerzielen erzielenwir wirErkenntnisse Erkenntnissenur nurdurch durchrein reinlogische logische Argumentation. Das ist gut: Die Ergebnisse sind so sicher Argumentation. Das ist gut: Die Ergebnisse sind so sicherwie wieinin keiner keineranderen anderenWissenschaft. Wissenschaft. •• Beispiele Beispiele Illustrieren Illustrierenund undmotivieren motivierenSätze Sätzeund undBeweise. Beweise. © Dr. Zschiegner 2008 Seite 4 Kapitel 1: Grundlagen Seite Inhalt Inhaltder derVorlesung Vorlesung 11Grundlagen Grundlagen Mengen, Mengen,Abbildungen, Abbildungen,Logik, Logik,Beweisen, Beweisen,Kombinatorik Kombinatorik 22Algebra Algebra Zahlen, Zahlen,(Un-) (Un-)Gleichungen, Gleichungen,Gleichungssysteme, Gleichungssysteme,Potenzen Potenzen&&Co. Co. 33Analytische AnalytischeGeometrie Geometrie Koordinaten, Koordinaten,Vektoren, Vektoren,Geraden, Geraden,Ebenen, Ebenen,Anwendungen Anwendungen 44Analysis Analysis Folgen, Folgen,Reihen, Reihen,Grenzwerte, Grenzwerte,Differenzialrechnung Differenzialrechnung © Dr. Zschiegner 2008 Seite 5 Kapitel 1: Grundlagen SPIC SPIC •• SPIC SPIC==Students StudentsPersonal PersonalInformation InformationCenter Center •• www.studiumplus.de www.studiumplus.deÆ ÆStudium StudiumÆ ÆSPIC SPIC •• Download Downloadder derFolien Folienund undweiterer weitererMaterialien Materialien •• Forum Forumund undNews Newszur zurVorlesung Vorlesung © Dr. Zschiegner 2008 Seite 6 Kapitel 1: Grundlagen Seite Kapitel Kapitel 11 Grundlagen Grundlagen © Dr. Zschiegner 2008 Seite 7 Kapitel 1: Grundlagen Inhalt Inhalt 1.1 1.1Mengen Mengen {{},},∈, ∈,... ... 1.2 1.2Abbildungen Abbildungen f:f:XX→ →YY 1.3 1.3Logik Logik ⇒, ⇒,∨, ∨,... ... 1.4 1.4Beweisen Beweisenmit mitvollständiger vollständigerInduktion Induktion 11++22++33++… + n … + n==?? 1.5 1.5Kombinatorik Kombinatorik n!, n!, n k © Dr. Zschiegner 2008 Seite 8 Kapitel 1: Grundlagen Seite 1.1 1.1Mengen Mengen © Dr. Zschiegner 2008 Seite 9 Kapitel 1: Grundlagen Was Wasist isteine eineMenge? Menge? •• Schwierige SchwierigeFrage! Frage! •• Der Der„Vater „Vaterder derMengenlehre“, Mengenlehre“,Georg GeorgCantor Cantor(1845 (1845--1918), 1918),sagte: sagte: „Unter einer Menge verstehen wir jede Zusammenfassung M „Unter einer Menge verstehen wir jede Zusammenfassung M von von bestimmten, bestimmten,wohlunterschiedenen wohlunterschiedenenObjekten Objekten m m unserer unserer Anschauung oder unseres Denkens ... zu einem Ganzen.“ Anschauung oder unseres Denkens ... zu einem Ganzen.“ •• Anstatt Anstattgenau genauzu zusagen, sagen,was waseine eineMenge Mengeist, ist,stellen stellenwir wirdar, dar,wie wie man manMengen Mengenbeschreiben beschreibenkann. kann.Dafür Dafürgibt gibtes esdrei dreiMöglichkeiten. Möglichkeiten. 1. 1.Durch DurchAufzählung Aufzählung 2. Durch Eigenschaften 2. Durch Eigenschaften 3. 3.Das Daskartesische kartesischeProdukt Produkt © Dr. Zschiegner 2008 Seite 10 Kapitel 1: Grundlagen Seite 1.1.1 1.1.1Beschreibung Beschreibungdurch durch Aufzählung Aufzählung •• Beispiel: Beispiel:{rot, {rot,grün, grün,blau} blau} ist istdie dieMenge Mengeder derFarben Farbenrot, rot,grün grünund und blau. blau. •• Beispiel: Beispiel:Die DieMenge Menge{Susanne, {Susanne,Yvonne, Yvonne,Ute, Ute,Nicole} Nicole} besteht bestehtaus aus den denElementen ElementenSusanne, Susanne,Yvonne, Yvonne,Ute, Ute,Nicole. Nicole. •• Beispiel: Beispiel:Wir Wirbetrachten betrachtenoft oftMengen Mengenvon vonZahlen: Zahlen: M M=={0, {0,1, 1,2, 2,3, 3,4} 4} ist istdie dieMenge Mengeder derZahlen Zahlen 0, 0,1, 1,2, 2,3, 3,4. 4. © Dr. Zschiegner 2008 Seite 11 Kapitel 1: Grundlagen Notation Notationund undBemerkung Bemerkung •• Die DieElemente Elementeder derMenge Mengewerden werdenin ingeschweifte geschweifteKlammern Klammern geschrieben: geschrieben: a, a,b, b,cc sind sinddie dieElemente Elementeder derMenge Menge {a, {a,b, b,c}. c}. •• Bei Beieiner einerMenge Mengespielt spieltdie dieReihenfolge Reihenfolgeder derElemente Elementekeine keine Rolle: Rolle: {c, {c,a, a,b} b}=={b, {b,a, a,c} c}=={a, {a,b, b,c}. c}. •• In Ineiner einerMenge Mengewerden werdenElemente, Elemente,die diemehrfach mehrfachauftauchen, auftauchen,nur nur einmal betrachtet: einmal betrachtet: {a, {a,a, a,a, a,a, a,b, b,b, b,b, b,c, c,c, c,c, c,c, c,c, c,c, c,c, c,c} c}=={a, {a,b, b,c}. c}. © Dr. Zschiegner 2008 Seite 12 Kapitel 1: Grundlagen Seite Unendliche UnendlicheMengen Mengen •• N: N:Menge Mengeder dernatürlichen natürlichenZahlen: Zahlen: NN=={0, {0,1, 1,2, 2,3, 3,4, 4,...}. ...}. •• Z: Z:Menge Mengeder derganzen ganzenZahlen: Zahlen: ZZ=={..., {...,–3, –3,–2, –2,–1, –1,0, 0,1, 1,2, 2,3, 3,...}. ...}. •• Q: Q:Menge Mengeder derrationalen rationalenZahlen Zahlen(„Brüche”). („Brüche”). •• R: R:Menge Mengeder derreellen reellenZahlen. Zahlen. © Dr. Zschiegner 2008 Seite 13 Kapitel 1: Grundlagen Elemente, Elemente,Teilmengen Teilmengen •• m m∈∈M: M:Das DasElement Element m m ist istininder derMenge Menge M M enthalten. enthalten. •• m m∉∉M: M:Das DasElement Element m m ist istnicht nichtininder derMenge Menge M M enthalten. enthalten. •• M M11⊆⊆M M22(„Teilmenge“): („Teilmenge“):Jedes JedesElement Elementvon von M M11 ist istauch auchein einElement Element . von M 2 von M . 2 •• Beispiel: Beispiel: M M1 =={rot, {rot,blau} blau} ist istTeilmenge Teilmengevon von M M2 =={rot, {rot,blau, blau,grün}. grün}. 1 2 •• Die Dieleere leereMenge Mengeenthält enthältkein keinElement. Element.Sie Siewird wirdmit mit {}{} oder oder ∅ ∅ bezeichnet. bezeichnet. © Dr. Zschiegner 2008 Seite 14 Kapitel 1: Grundlagen Seite 1.1.2 1.1.2 Beschreibung Beschreibung einer einer Menge Mengedurch durchEigenschaften Eigenschaften •• Wichtiges WichtigesPrinzip: Prinzip:Man Mansondert sondertaus auseiner einerschon schonvorhandenen vorhandenen Menge eine Teilmenge aus. Menge eine Teilmenge aus. •• Man Mannennt nenntdas dasauch auch„Mengenbildung „Mengenbildungdurch durchAussonderung“ Aussonderung“ •• Beispiele: Beispiele: 1. 1.TT==Menge Mengealler allerTiere. Tiere.M M=={t{t∈∈TT| |tt ist istintelligent}. intelligent}.(Klassische (Klassische Definition Definitiondes desMenschen) Menschen) 2. 2.GG=={z {z∈∈ZZ| |zz ist istgerade}. gerade}. Eigenschaft: Eigenschaft:„gerade „geradesein“. sein“. Es Esist ist GG=={..., {...,–4, –4,–2, –2,0, 0,2, 2,4, 4,...}. ...}. © Dr. Zschiegner 2008 Seite 15 Kapitel 1: Grundlagen Aufgaben Aufgaben Stellen StellenSie Siefolgende folgendeMengen Mengenininaufzählender aufzählenderForm Formdar: dar: (a) (a) AA=={x {x∈∈NN| ||x|x++1| 1|≤≤4} 4} (b) (b) BB=={p {p∈∈NN| |ppist istPrimzahl Primzahlund undpp≤≤35} 35} © Dr. Zschiegner 2008 Seite 16 Kapitel 1: Grundlagen Seite Intervalle Intervalle Für Fürzwei zweireelle reelleZahlen Zahlenaaund undbbmit mitaa<<bbschreiben schreibenwir: wir: •• (a, (a,b) b)=={x∈R {x∈R| |a<x<b} a<x<b} „offenes „offenesIntervall“, Intervall“, •• (a, (a,b] b]=={x∈R {x∈R| |a<x≤b} a<x≤b} „linksseitig „linksseitighalboffenes halboffenesIntervall“, Intervall“, •• [a, [a,b) b)=={x∈R {x∈R| |a≤x<b} a≤x<b} „rechtsseitig „rechtsseitighalboffenes halboffenesIntervall“, Intervall“, •• [a, [a,b] b]=={x∈R {x∈R| |a≤x≤b} a≤x≤b} „geschlossenes „geschlossenesIntervall“. Intervall“. © Dr. Zschiegner 2008 Seite 17 Kapitel 1: Grundlagen Durchschnitt Durchschnitt(Schnittmenge) (Schnittmenge) •• Der DerDurchschnitt Durchschnittzweier zweierMengen Mengen M M11 und und M M22 ist istso sodefiniert: definiert: M M22=={m {m∈∈M M11| |m m∈∈M M22}}(= (={m {m∈∈M M22| |m m∈∈M M11}). }). M11∩∩M Eigenschaft: Eigenschaft:“m “m∈∈M M22””.. •• Beispiel: Menge der der Biologiestudenten, Biologiestudenten, M M22:: Menge Menge der der MatheMatheBeispiel: M M11:: Menge matikstudenten. Dann ist M ∩ M die Menge der Studenten, matikstudenten. Dann ist M11 ∩ M22 die Menge der Studenten, die die sowohl sowohlBio Bioals alsauch auchMathe Mathestudieren. studieren. •• Beispiel: Beispiel: GG == Menge Menge der der geraden geraden natürlichen natürlichen Zahlen, Zahlen, DD == Menge Menge der durch 3 teilbaren natürlichen Zahlen. Dann ist G ∩ D die Menge der durch 3 teilbaren natürlichen Zahlen. Dann ist G ∩ D die Menge der derdurch durch66teilbaren teilbarennatürlichen natürlichenZahlen. Zahlen. © Dr. Zschiegner 2008 Seite 18 Kapitel 1: Grundlagen Seite Schnittmengen Schnittmengenim imVenn-Diagramm Venn-Diagramm © Dr. Zschiegner 2008 Seite 19 Kapitel 1: Grundlagen Disjunkte DisjunkteMengen Mengen •• Zwei ZweiMengen Mengenheißen heißendisjunkt disjunkt(oder (oderauch auch„elementfremd“), „elementfremd“), wenn sie kein Element gemeinsam haben. wenn sie kein Element gemeinsam haben. Formaler: Formaler:M M11 und und M M22 werden werdendisjunkt disjunktgenannt, genannt,falls falls M M11∩∩M M22=={}{} gilt. gilt. •• Beispiel: Beispiel:Sei Sei CC die dieMenge Mengeder derMitglieder Mitgliederder derCDU, CDU,SS die dieMenge Menge der Mitglieder der SPD. Dann sind C und S disjunkte Mengen. der Mitglieder der SPD. Dann sind C und S disjunkte Mengen. •• Beispiel: Beispiel:Die DieMenge Mengeder derdurch durch 44 teilbaren teilbarenZahlen Zahlenund unddie dieMenge Menge der Primzahlen sind disjunkt. der Primzahlen sind disjunkt. © Dr. Zschiegner 2008 Seite 20 Kapitel 1: Grundlagen Seite Vereinigungsmenge Vereinigungsmenge •• Die DieVereinigung Vereinigungzweier zweierMengen Mengen M M11 und und M M22 ist istso sodefiniert: definiert: M M22=={m {m| |m m∈∈M M11 oder oder m m∈∈M M22}.}. M11∪∪M •• Beispiel: Mengeder derBiologiestudenten, Biologiestudenten,M M22::Menge Mengeder der Beispiel:M M11::Menge Mathematikstudenten. Dann ist M ∪ M die Menge der Mathematikstudenten. Dann ist M1 ∪ M2 die Menge derStudenten, Studenten, 1 2 die dieBio Biooder oderMathe Mathe(oder (oderbeides) beides)studieren. studieren. Bemerkung: Bemerkung:Wenn Wennwir wir„oder“ „oder“sagen sagenmeinen meinenwir wirimmer immerdas dasnichtnichtausschließliche Oder. ausschließliche Oder. •• Beispiel: Beispiel:GG==Menge Mengeder dergeraden geradennatürlichen natürlichenZahlen, Zahlen,UU==Menge Menge der ungeraden natürlichen Zahlen. Dann ist G ∪ U = N. der ungeraden natürlichen Zahlen. Dann ist G ∪ U = N. © Dr. Zschiegner 2008 Seite 21 Kapitel 1: Grundlagen Aufgaben Aufgaben Bestimmen BestimmenSie Siedie diefolgenden folgendenMengen: Mengen: (a) (a){rot, {rot,blau, blau,gelb} gelb}∩∩{grün, {grün,gelb, gelb,lila}, lila}, (b) (b){rot, {rot,blau, blau,gelb} gelb}∪∪{grün, {grün,gelb, gelb,lila}, lila}, (c) (c)NN∩∩{grün, {grün,gelb, gelb,lila}, lila}, (d) (d)NN∪∪{grün, {grün,gelb, gelb,lila}, lila}, (e) (e)NN∩∩Z, Z, (f) (f)NN∪∪Z. Z. © Dr. Zschiegner 2008 Seite 22 Kapitel 1: Grundlagen Seite Differenz Differenz von von Mengen Mengen •• Die DieDifferenz Differenzzweier zweierMengen Mengen M M11 und und M M22 ist istso sodefiniert: definiert: M M22=={m {m∈∈M M11| |m m∉∉M M22}.}. M11\\M Eigenschaft: Eigenschaft: “m “m∉∉M M2”.”. 2 •• Beispiele: Beispiele:{rot, {rot,blau, blau,gelb}\{grün, gelb}\{grün,weiß, weiß,rot} rot}=={blau, {blau,gelb} gelb} Z\G = Menge der ungeraden ganzen Zahlen Z\G = Menge der ungeraden ganzen Zahlen N\G N\G ==Menge Mengeder derungeraden ungeradennatürlichen natürlichenZahlen. Zahlen. •• Bemerkungen: Bemerkungen: 1. 1.Wir Wirbenutzen benutzen“\” “\” anstelle anstellevon von “–”. “–”. 2. 2.Man Mandarf darf M M11\M \M22 auch auchdann dannbilden, bilden,wenn wenn M M22 keine keineTeilmenge Teilmenge von von M M1 ist. ist. 1 © Dr. Zschiegner 2008 Seite 23 Kapitel 1: Grundlagen Komplement Komplement einer einer Menge Menge •• Wenn Wenndie dieMenge Menge M M22 eine eineTeilmenge Teilmengevon von M M11 ist, ist,so sonennt nenntman mandie die Differenz M \M das Komplement von M in M . Differenz M1 \M2 das Komplement von M2 in M1 . 1 2 2 •• Zwei Zwei Teilmengen Teilmengen M M22 und und M M11 komplementär genannt, wenn gilt komplementär genannt, wenn gilt 1 einer einer Menge Menge M M werden werden M M11∪∪M M22==M M und undM M11∩∩M M22=={}. {}. (Man (Mankann kannauch auchsagen: sagen:… …wenn wenn M M22==M\M M\M11 ist.) ist.) •• Beispiel: Beispiel: M M11 == {2, {2, 4, 4, 6}, 6}, M M22 == {1, {1, 3, 3, 5} 5} sind sind komplementäre komplementäre TeilTeilmengen von {1, 2, 3, 4, 5, 6}. mengen von {1, 2, 3, 4, 5, 6}. © Dr. Zschiegner 2008 Seite 24 Kapitel 1: Grundlagen Seite Aufgaben Aufgaben Bestimmen BestimmenSie Siedie diefolgenden folgendenMengen: Mengen: (a) (a){rot, {rot,blau, blau,gelb} gelb}\\{grün, {grün,gelb, gelb,lila}, lila}, (b) (b){rot, {rot,blau, blau,gelb} gelb}\\{blau, {blau,gelb, gelb,rot}, rot}, (c) (c)NN\\{grün, {grün,gelb, gelb,lila}, lila}, (d) (d){rot, {rot,blau, blau,gelb} gelb}\\N, N, (e) (e)NN\\Z, Z, (f) (f)ZZ\\N. N. © Dr. Zschiegner 2008 Seite 25 Kapitel 1: Grundlagen 1.1.3 1.1.3 Das Daskartesische kartesischeProdukt Produkt •• Ziel: Ziel:Mengen Mengenganz ganzneuen neuenTyps! Typs! •• Seien Seien M M11 und und M M22 zwei zwei Mengen Mengen mit mit M M11,, M M22 ≠≠ {}. {}. Dann Dann ist ist das das kartesische Produkt die Menge M ×M , die aus allen geordneten kartesische Produkt die Menge M11×M22, die aus allen geordneten Paaren Paaren (m (m1,,m m2)) mit mit m m1 ∈∈M M1 und und m m2 ∈∈M M2 besteht. besteht. 1 2 1 1 2 2 •• Beispiel: {0,1, 1,2} 2} und und M M22=={a, {a,b}, b},so sogilt gilt Beispiel:Ist Ist M M11=={0, M ×M22=={(0, {(0,a), a),(0, (0,b), b),(1, (1,a), a),(1, (1,b), b),(2, (2,a), a),(2, (2,b)}. b)}. M11×M •• Achtung: Achtung: Bei Bei den den Paaren Paaren kommt kommt es es auf auf die die Reihenfolge Reihenfolge an! an! Zum Zum Beispiel ×M2.. Beispielist istdas dasPaar Paar (a, (a,0) 0) kein keinElement Elementder derobigen obigenMenge Menge M M1×M 1 2 © Dr. Zschiegner 2008 Seite 26 Kapitel 1: Grundlagen Seite Das Dasallgemeine allgemeinekartesische kartesischeProdukt Produkt •• Seien Seien M M11,,M M22,,..., ...,M Mnn nichtleere nichtleereMengen, Mengen,dann dannist istdas daskartesische kartesische Produkt Produktdieser dieserMengen Mengendefiniert definiertdurch: durch: M ×M22××......×M ×Mnn=={(m {(m11,,m m22,,..., ...,m mnn))m m11∈∈M M11,,m m22∈∈M M22,,..., ...,m mnn∈∈M Mnn}} M11×M •• Beispiel: Beispiel:Seien Seien He, He,Ho, Ho,SS die dieMengen Mengender derHemden, Hemden,Hosen Hosenund und Schuhen von Professor X. Dann beschreibt die Menge He×Ho×S Schuhen von Professor X. Dann beschreibt die Menge He×Ho×S die dieMöglichkeiten Möglichkeitenvon vonProfessor ProfessorX, X,sich sichzu zukleiden. kleiden. •• Beispiel: Beispiel:Für FürAA=={1, {1,2, 2,3}, 3},BB=={a, {a,b} b}und undCC=={x, {x,y} y}ist ist AA××BB××CC=={(1,a,x), (1,a,y), (1,b,x), (1,b,y), (2,a,x), (2,a,y), {(1,a,x), (1,a,y), (1,b,x), (1,b,y), (2,a,x), (2,a,y),(2,b,x), (2,b,x), (2,b,y), (2,b,y),(3,a,x), (3,a,x),(3,a,y), (3,a,y),(3,b,x), (3,b,x),(3,b,y)} (3,b,y)}.. © Dr. Zschiegner 2008 Seite 27 Kapitel 1: Grundlagen Das Das kartesische kartesische Produkt: Produkt: Bemerkungen Bemerkungen •• Die DieBezeichnung Bezeichnung“kartesisch” “kartesisch”(früher (früherauch auch„cartesisch“) „cartesisch“)geht gehtauf aufden den Mathematiker und Philosophen René Descartes (1596 1650) Mathematiker und Philosophen René Descartes (1596 - 1650) zurück. zurück. In Inder derMathematik Mathematikwird wirdsein seinName Namedamit damitverbunden, verbunden,dass dasser erdie die Punkte Punkteder derEbene Ebenedurch durchPaare Paarevon vonZahlen Zahlendargestellt dargestellthat hat(siehe (siehe Kapitel 3). Kapitel 3). •• Die DieElemente Elementevon von M M11×M ×M22××......×M ×Mnn tragen tragenvielfältige vielfältigeNamen: Namen: n-Tupel, n-Tupel,Folgen Folgender derLänge Länge n. n. Statt Statt2-Tupel 2-Tupelsagt sagtman manPaar, Paar,statt statt3-Tupel 3-Tupelsagt sagtman manTripel. Tripel. © Dr. Zschiegner 2008 Seite 28 Kapitel 1: Grundlagen Seite Aufgabe Aufgabe Bestimmen BestimmenSie Siedas daskartesische kartesischeProdukt ProduktAAxxBBfür fürdie dieMengen Mengen AA=={Stufenheck, {Stufenheck,Fließheck, Fließheck,Kombi}, Kombi}, BB=={Automatik, {Automatik,Handschaltung}. Handschaltung}. © Dr. Zschiegner 2008 Seite 29 Kapitel 1: Grundlagen 1.1.4 1.1.4 Mächtigkeiten Mächtigkeiten •• Sei Sei M M eine eineMenge. Menge. Wir bezeichnen Wir bezeichnenwir wirdie dieAnzahl Anzahlder derElemente Elementevon von M M mit mit M. M.Diese Diese Zahl Zahlheißt heißtMächtigkeit Mächtigkeit(oder (oderKardinalität) Kardinalität)von von M. M. •• Beispiel: Beispiel: {0,1,2,3} {0,1,2,3}==4. 4. •• Eine EineMenge Mengewird wirdendlich endlichgenannt, genannt,wenn wennihre ihreMächtigkeit Mächtigkeiteine eine natürliche Zahl ist. natürliche Zahl ist. •• Sonst Sonstheißt heißtdie dieMenge Mengeunendlich. unendlich.Wenn Wenn M M eine eineunendliche unendlicheMenge Menge ist, so schreiben wir M = ∞. ist, so schreiben wir M = ∞. •• Beispiel: Beispiel:N N==∞∞ und und Z Z==∞. ∞. © Dr. Zschiegner 2008 Seite 30 Kapitel 1: Grundlagen Seite Mächtigkeit Mächtigkeitdes desKomplements Komplements 1.1.1 1.1.1 Satz. Satz. Sei Sei M M11 eine eine endliche endliche Menge, Menge, und und sei sei M M22 eine eine Teilmenge von M . Dann gilt: Teilmenge von M1 . Dann gilt: 1 M \M22==M M11––M M22. . M11\M Beispiel: Beispiel: Anzahl Anzahl der der männlichen männlichen Einwohner Einwohner der der Bundesrepublik Bundesrepublik == Gesamtbevölkerungszahl Gesamtbevölkerungszahlminus minusAnzahl Anzahlder derFrauen. Frauen. Beweis. Beweis.Zu Zuzeigen: zeigen:Auf Aufbeiden beidenSeiten Seitensteht stehtdie diegleiche gleicheZahl! Zahl! Linke LinkeSeite: Seite: Anzahl Anzahlder derElement Elementvon von M M1\M \M2.. 1 2 Rechte RechteSeite: Seite:Wir Wirzählen zählenzuerst zuerstdie dieAnzahl Anzahlder derElemente Elementevon von M M11,, dann ziehen wir die Elemente von M wieder ab. Daher erhalten dann ziehen wir die Elemente von M2 wieder ab. Daher erhaltenwir wir 2 auch auchauf aufder derrechten rechtenSeite Seitedie dieAnzahl Anzahlder derElemente Elementevon von M M11\M \M22.. © Dr. Zschiegner 2008 Seite 31 Kapitel 1: Grundlagen Summenformel Summenformel 1.1.2 1.1.2Satz. Satz.Seien Seien M M11 und und M M22 endliche endlicheMengen. Mengen.Dann Danngilt gilt M M22==M M11++M M22––M M11∩∩M M22. . M11∪∪M Beispiel: Beispiel:Für Fürdie dieAnzahl Anzahlder derStudierenden, Studierenden,die dieMathematik Mathematikstudieren studieren oder Sport studieren, muss man wissen, (a) wie viele Leute Matheoder Sport studieren, muss man wissen, (a) wie viele Leute Mathematik matikstudieren, studieren,(b) (b)wie wieviele vieleSport Sportstudieren studierenund und(c) (c)wie wieviele viele Mathematik und Sport studieren. Mathematik und Sport studieren. © Dr. Zschiegner 2008 Seite 32 Kapitel 1: Grundlagen Seite Summenformel: Summenformel: Der Der Beweis Beweis Beweis Beweis(= (=warum warumist istdas dasso?). so?). Zu Zuzeigen: zeigen:Auf Aufbeiden beidenSeiten Seitensteht stehtdie diegleiche gleicheZahl! Zahl! Linke M22 wird wirdgenau genaueinmal einmalgezählt. gezählt. LinkeSeite: Seite:Jedes JedesElement Elementvon vonM M11∪∪M Rechte Seite: In M + M wird jedes Element von M und Rechte Seite: In M11 + M22 wird jedes Element von M11 und jedes jedesElement Elementvon von M M2 einmal einmalgezählt, gezählt, 2 die ∩M22 werden werdenalso alsodoppelt doppeltgezählt. gezählt. dieElemente Elementevon von M M11∩M Dies wird dadurch korrigiert, dass M ∩ M wieder Dies wird dadurch korrigiert, dass M11 ∩ M22 wiederabgezogen abgezogen wird. wird. Daher Daherwird wirdauch auchauf aufder derrechten rechtenSeite Seitejedes jedesElement Elementgenau genaueinmal einmal gezählt. gezählt. © Dr. Zschiegner 2008 Seite 33 Kapitel 1: Grundlagen Aufgabe Aufgabe Bestimmen BestimmenSie SieA A∪∪BB∪∪C Cfür fürjejedrei dreiendliche endliche Mengen Mengen A, A,B, B,C. C. © Dr. Zschiegner 2008 Seite 34 Kapitel 1: Grundlagen Seite Aufgabe Aufgabe Welche Welcheder derAussagen Aussagensind sindfür fürbeliebige beliebigeMengen Mengen XX und und YY richtig? richtig? (a) (a)Wenn Wenn XX\\YY==∅ ∅ ist, ist,dann danngilt gilt XX==Y. Y. (b) (b)XX∩∩YY=={m {m| |m m∈∈XXund undm m∈∈Y}. Y}. (c) (c)|X |X∪∪Y| Y|==|X| |X|++|Y|. |Y|. (d) (d)Wenn Wenn XX∪∪YY endlich endlichist, ist,dann dannsind sindauch auch XX und und YY endlich. endlich. (e) (e)Wenn Wenn XX∩∩YY endlich endlichist, ist,dann dannsind sindauch auch XX und und YY endlich. endlich. Begründen BegründenSie SieIhre IhreEntscheidung, Entscheidung,indem indemSie Sieentweder entwederein einArgument Argument für die Richtigkeit der Aussage oder ein Gegenbeispiel angeben. für die Richtigkeit der Aussage oder ein Gegenbeispiel angeben. © Dr. Zschiegner 2008 Seite 35 Kapitel 1: Grundlagen Die DieProduktformel Produktformel 1.1.3 1.1.3Satz. Satz.Seien Seien M M11,,M M22 nichtleere nichtleereendliche endlicheMengen. Mengen.Dann Danngilt: gilt: M ×M22==M M11⋅ ⋅M M22. . M11×M Beispiel: Beispiel:In Ineinem einemRaum Raumbefinden befindensich sich66Frauen Frauenund und44Männer. Männer. Dann kann man genau 6⋅4 = 24 getrennt geschlechtliche Dann kann man genau 6⋅4 = 24 getrennt geschlechtlichePaare Paare bilden. bilden. Beispiel: Beispiel:Die DieAnzahl Anzahlaller allerPaare Paare (x, (x,y), y), wobei x aus der Menge {0, 1, 2, ..., 9} wobei x aus der Menge {0, 1, 2, ..., 9} und und yy aus ausder derMenge Menge {a, {a,b, b,c,c,d, d,..., ...,z} z} stammt, stammt, ist 10⋅26 = 260. ist 10⋅26 = 260. © Dr. Zschiegner 2008 Seite 36 Kapitel 1: Grundlagen Seite Die DieProduktformel: Produktformel:Der DerBeweis Beweis Beweis Beweis(= (=warum warumist istdie dieFormel Formelrichtig?). richtig?). Die Menge M ×M besteht aus allen 1 2 Die Menge M ×M besteht aus allenPaaren Paaren (m (m1,,m m2)) mit mit m m1 ∈∈M M1 1 2 1 2 1 1 und und m m22∈∈M M22..Wir Wirmüssen müssendie dieAnzahl Anzahldieser dieserPaare Paareberechnen. berechnen. Für Fürdie dieerste ersteKomponente Komponente(also (alsofür für m m11)) haben habenwir wirgenau genau M M11 Möglichkeiten Möglichkeitenzu zuAuswahl. Auswahl. Für Fürjede jededieser dieserMöglichkeiten Möglichkeitenkönnen könnenwir wirdie diezweite zweiteKomponente Komponente m m2 inin M M2 ohne ohnejede jedeEinschränkung Einschränkungwählen. wählen. 2 2 Dafür Dafürgibt gibtes es M M22 viele vieleMöglichkeiten. Möglichkeiten. Um m22)) zu zuwählen wählengibt gibtes esinsgesamt insgesamtalso alsogenau genau Umein einPaar Paar (m (m11,,m M M1⋅ ⋅M M2 Möglichkeiten. Möglichkeiten. 1 2 © Dr. Zschiegner 2008 Seite 37 Kapitel 1: Grundlagen Allgemeine AllgemeineProduktformel Produktformel 1.1.4 1.1.4Satz. Satz.Seien Seien M M11,,M M22,,..., ...,M Mnn endliche endlichenichtleere nichtleereMengen. Mengen.Dann Dann ist ist M ×M22××... ...×M ×Mnn==M M11⋅M ⋅M22⋅ ⋅... ...⋅M ⋅Mnn. . M11×M Beispiel. Beispiel. Wenn Wenn Professor Professor XX genau genau 88 Hemden, Hemden, 33 Hosen Hosen und und 44 Paar Paar Schuhe hat, so kann er sich auf 8⋅3⋅4 = 96 Weisen kleiden. Schuhe hat, so kann er sich auf 8⋅3⋅4 = 96 Weisen kleiden. Beispiel. Beispiel.Bei BeiGeldausgabeautomaten Geldausgabeautomatenbesteht bestehtdie dieGeheimzahl Geheimzahlaus aus vier Dezimalstellen. Wie viele PINs gibt es, bei denen die erste Stelle vier Dezimalstellen. Wie viele PINs gibt es, bei denen die erste Stelle nicht nicht 00ist? ist? Antwort: Antwort:9⋅10⋅10⋅10 9⋅10⋅10⋅10==9000. 9000. © Dr. Zschiegner 2008 Seite 38 Kapitel 1: Grundlagen Seite Aufgabe Aufgabe In Inmeinem meinemLieblingssteakrestaurant Lieblingssteakrestaurantkann kannman mansich sichseine seineMahlzeit Mahlzeitaus aus folgenden Komponenten selbst zusammenstellen: folgenden Komponenten selbst zusammenstellen: (a) (a)Hüftsteak, Hüftsteak,Rumpsteak, Rumpsteak,Filetsteak, Filetsteak,Rib-Eye Rib-EyeSteak; Steak; (b) Gewicht: 180g oder 250g; (b) Gewicht: 180g oder 250g; (c) (c)Beilagen: Beilagen:Folienkartoffeln, Folienkartoffeln,Pommes PommesFrites, Frites,Kroketten, Kroketten,Bratkartoffeln, Bratkartoffeln, weißer Langkornreis, Maiskolben, Knoblauchbrot, rote Bohnen, weißer Langkornreis, Maiskolben, Knoblauchbrot, rote Bohnen, Zwiebelringe, Zwiebelringe,Champignons; Champignons; (d) Saucen: Kräuterbutter, (d) Saucen: Kräuterbutter,Pfefferrahmsauce, Pfefferrahmsauce,Sauce Saucen. n.Art ArtBéarnaise. Béarnaise. Wenn Wennich ichjeden jedenMonat Monateinmal einmaldort dortesse: esse:Wie Wielange langebrauche braucheich, ich,um um alle Kombinationen durchzuprobieren? Was hat das Ganze mit dem alle Kombinationen durchzuprobieren? Was hat das Ganze mit dem kartesischen kartesischenProdukt Produktzu zutun? tun? © Dr. Zschiegner 2008 Seite 39 Kapitel 1: Grundlagen Aufgabe Aufgabe Seien Seien M M11 und und M M22 Mengen. Mengen.Wir Wirdefinieren definierendie diesymmetrische symmetrische Differenz von M und M durch Differenz von M1 und M2 durch 1 2 M M22==(M (M11∪∪M M22))\\(M (M11∩∩M M22).). M11∆∆M (a) (a)Beschreiben BeschreibenSie Siedie diesymmetrische symmetrischeDifferenz DifferenzininWorten. Worten. (b) (b)Machen MachenSie Siesich sichdie diesymmetrische symmetrischeDifferenz Differenzan aneinem einemVennVennDiagramm klar. Diagramm klar. (c) (c)Wenn Wenn M M11 und und M M22 endliche endlicheMengen Mengensind, sind,können könnenSie Siedann danndie die Mächtigkeit M2 angeben? angeben? Mächtigkeitvon vonM M1 ∆∆M 1 2 © Dr. Zschiegner 2008 Seite 40 Kapitel 1: Grundlagen Seite 1.1.5 1.1.5 Relationen Relationen © Dr. Zschiegner 2008 Seite 41 Kapitel 1: Grundlagen Beispiele Beispielefür fürRelationen Relationen © Dr. Zschiegner 2008 Seite 42 Kapitel 1: Grundlagen Seite Aufgaben Aufgaben 1. 1. Sei SeiAA==BB==ZZ(= (=ganze ganzeZahlen). Zahlen).Bestimmen BestimmenSie Siedie dieRelation Relationvon vonAA ininB, B,die diealle allePaare Paare(a, (a,b) b)mit mita² a²++b² b²==25 25enthält. enthält. 2. 2. Sei SeiAA==BB==NN(= (=natürliche natürlicheZahlen). Zahlen).Bestimmen BestimmenSie Siedie dieRelation Relation von vonAAininB, B,die diealle allePaare Paare(a, (a,b) b)mit mita² a²++bb==44enthält. enthält. Welche Welcheder derbeiden beidenobigen obigenRelationen Relationenordnet ordneteiner einerZahl Zahlaaeindeutig eindeutig eine eineZahl Zahlbbzu? zu? © Dr. Zschiegner 2008 Seite 43 Kapitel 1: Grundlagen 1.2 1.2Abbildungen Abbildungen © Dr. Zschiegner 2008 Seite 44 Kapitel 1: Grundlagen Seite Abbildungen Abbildungen==Funktionen Funktionen Seien SeienXXund undYYMengen. Mengen.Eine EineRelation Relationffvon vonXXininYYheißt heißtFunktion Funktion (oder Abbildung) von X in Y, wenn es für jedes x ∈ X genau (oder Abbildung) von X in Y, wenn es für jedes x ∈ X genauein einyy∈∈YY gibt, gibt,so sodass dass(x, (x,y) y)∈∈ffist. ist. Kurz: Kurz:„Funktionen „Funktionensind sindeindeutige eindeutigeRelationen.“ Relationen.“ Beispiel: Beispiel:Die DieRelation Relationf,f,die diedie diePaare Paare(x, (x,y) y)∈∈RR××RRenthält, enthält,für fürdie die yy==2x gilt, ist eine Funktion. 2x gilt, ist eine Funktion. Anders Andersausgedrückt: ausgedrückt:Eine EineFunktion Funktion(oder (oderAbbildung) Abbildung)von von XX nach nach YY ist eine Vorschrift, ist eine Vorschrift, die diejedem jedemElement Elementvon von XX genau genauein einElement Elementvon von YY zuordnet. zuordnet. © Dr. Zschiegner 2008 Seite 45 Kapitel 1: Grundlagen Beispiele Beispielevon vonAbbildungen Abbildungen •• Zuordnung Zuordnung Ware Ware→ →Preis Preis ist isteine eineAbbildung. Abbildung. Hier ist X die Menge der Waren und Hier ist X die Menge der Waren und YY die dieMenge Mengeder derPreise. Preise.Jede Jede Ware Warehat hateinen eineneindeutigen eindeutigenPreis; Preis;also alsoist istdie dieZuordnung Zuordnungeine eine Abbildung. Abbildung. •• Zuordnung Zuordnung Person Person→ →Körpergröße Körpergröße ist isteine eineAbbildung. Abbildung. X: Menge aller Personen, Y: Menge der natürlichen X: Menge aller Personen, Y: Menge der natürlichenZahlen. Zahlen. Die DieKörpergröße Körpergrößeeiner einerPerson Personist isteindeutig. eindeutig. Es Eskann kannsein, sein,dass dassmehrere mehrerePersonen Personendieselbe dieselbeGröße Größehaben; haben;das dasist ist nicht nichtverboten. verboten. © Dr. Zschiegner 2008 Seite 46 Kapitel 1: Grundlagen Seite Sprache Spracheder derAbbildungen Abbildungen •• Für Füreine eineAbbildung Abbildung ff von von XX nach nach YY schreiben schreibenwir wir f:f:XX→ →Y. Y. •• Jedem JedemElement Element xx∈∈XX wird wirdgenau genauein ein yy∈∈YY zugeordnet. zugeordnet.Dieses Dieses yy bezeichnen bezeichnenwir wirmit mit f(x). f(x). •• Bezeichnung: Bezeichnung: f:f:XX→ →Y: Y:yy==f(x) f(x) oder oder f:f:XX→ →Y: Y:xx→ →f(x). f(x). X: X: Definitionsbereich, Definitionsbereich,Y: Y: Bildbereich. Bildbereich. © Dr. Zschiegner 2008 Seite 47 Kapitel 1: Grundlagen Mathematische Mathematische Beispiele Beispiele •• Sei Sei ff die dieAbbildung Abbildungder derMenge Menge {1,2,3} {1,2,3} ininsich, sich,die diefolgendermaßen folgendermaßen erklärt erklärtist ist 11→ →1, 1,22→ →3, 3,33→ →2. 2. 2 •• Die isteine eineAbbildung. Abbildung. DieVorschrift Vorschrift f:f:RR→ →R, R,definiert definiertdurch durch f(x) f(x)==xx2,,ist Bemerkung: Bemerkung: Bei Bei Abbildungen Abbildungen von von RR inin sich sich verwendet verwendet man man meist meist den Begriff Funktion statt Abbildung. den Begriff Funktion statt Abbildung. •• Wir Wirordnen ordnenjeder jedernichtleeren nichtleerenTeilmenge Teilmengevon von NN ihr ihrkleinstes kleinstesElement Element zu. Das ergibt eine Abbildung; Definitionsbereich: Menge aller zu. Das ergibt eine Abbildung; Definitionsbereich: Menge aller nichtnichtleeren leerenTeilmengen Teilmengenvon von N, N,Bildbereich: Bildbereich: N. N. © Dr. Zschiegner 2008 Seite 48 Kapitel 1: Grundlagen Seite Darstellungen Darstellungenvon vonAbbildungen Abbildungen © Dr. Zschiegner 2008 Seite 49 Kapitel 1: Grundlagen Die DieIdentität Identität •• Wir Wirbetrachten betrachtenAbbildungen Abbildungeneiner einerMenge Menge XX ininsich. sich. •• Identität: Identität:ordnet ordnetjedem jedemElement Element xx aus aus XX wieder das Element x zu. wieder das Element x zu. •• Bezeichnung: Bezeichnung: idid oder odergenauer genauer ididXX.. •• Es Esgilt giltalso also = x für alle x ∈ X. ididX(x) X(x) = x für alle x ∈ X. © Dr. Zschiegner 2008 Seite 50 Kapitel 1: Grundlagen Seite Hintereinanderausführung Hintereinanderausführungvon vonAbbildungen Abbildungen •• Definition: Definition:Sei Sei g: g:XX→ →YY eine eineAbbildung Abbildungvon von XX nach nach Y, Y,und undsei sei f:f: YY→ →ZZ eine eineAbbildung Abbildungvon von YY nach nach Z. Z.Dann Dannist ist ff◦◦gg eine eine Abbildung Abbildungvon von XX nach nach Z, Z,wenn wennwir wirdefinieren definieren ff◦◦g: g:XX→ →Z: Z:xx→ →f(g(x)). f(g(x)). •• Man Man spricht spricht von von Hintereinanderausführung Hintereinanderausführung von von Abbildungen; Abbildungen; (oder: Verknüpfung, Verkettung, Komposition oder Produkt). (oder: Verknüpfung, Verkettung, Komposition oder Produkt). •• Achtung Achtung Reihenfolge! Reihenfolge! Für Für ff ◦◦ gg muss muss man man zuerst zuerst gg und und dann dann ff ausführen. ausführen.Man Manliest liest „f„f◦◦g“ g“ als als„f„f nach nach g” g” oder oder„erst „erst g, g,dann dann f”. f”. © Dr. Zschiegner 2008 Seite 51 Kapitel 1: Grundlagen Beispiele Beispiele Beispiel: Beispiel:Sei Sei XX=={0, {0,1, 1,2}, 2},YY=={a, {a,b, b,c}, c},ZZ=={α, {α,β, β,γ}. γ}.Seien Seien g: g:XX→ →YY und f: Y → Z die folgendermaßen definierten Abbildungen: und f: Y → Z die folgendermaßen definierten Abbildungen: g(0) g(0)==c,c,g(1) g(1)==a, a,g(2) g(2)==c;c;f(a) f(a)==β, β,f(b) f(b)==γ,γ,f(c) f(c)==α. α. Dann Dannist ist ff◦◦gg wie wiefolgt folgtdefiniert: definiert: (f(f◦◦g)(0) g)(1)==f(g(1)) f(g(1))==f(a) f(a)==β, β, g)(0)==f(g(0)) f(g(0))==f(c) f(c)==α, α,(f(f° °g)(1) (f(f◦◦g)(2) g)(2)==f(g(2)) f(g(2))==f(c) f(c)==α. α. Beispiel: Beispiel:Sei Sei gg die dieAbbildung, Abbildung,die dieeinem einemKraftfahrzeug Kraftfahrzeugseinen seinen Hubraum und f die Abbildung, die einem Hubraum die Hubraum und f die Abbildung, die einem Hubraum dieSteuerklasse Steuerklasse zuordnet. zuordnet.Dann Dannist ist ff◦◦gg die dieAbbildung, Abbildung,die dieeinem einemKraftfahrzeug Kraftfahrzeug seine Steuerklasse zuordnet. seine Steuerklasse zuordnet. © Dr. Zschiegner 2008 Seite 52 Kapitel 1: Grundlagen Seite Beispiel Beispiel 2 Beispiel: Beispiel:Seien Seienffund undggdie dieAbbildungen Abbildungenvon vonRRininsich sichmit mitf(x) f(x)==xx2und und g(x) g(x)==xx++5. 5. Dann Dannsind sindsowohl sowohlff◦◦ggals alsauch auchgg◦◦ffAbbildungen Abbildungenvon vonRRininsich sichmit mit (f(f◦◦g)(x) g)(x)==(x (x++5)², 5)², (g (g◦◦f)(x) f)(x)==x² x²++5. 5. © Dr. Zschiegner 2008 Seite 53 Kapitel 1: Grundlagen Aufgabe Aufgabe Die DieAbbildungen Abbildungen ff und und gg von vonRRininsich sichseien seiendurch durch f(x) f(x)==xx++11 und und g(x) = 2x definiert. g(x) = 2x definiert. (a) (a) Bilden BildenSie Siedie dieverkettete verketteteAbbildung Abbildung ffoog. g. (b) (b) Bilden BildenSie Siedie dieverkettete verketteteAbbildung Abbildung ggoof.f. © Dr. Zschiegner 2008 Seite 54 Kapitel 1: Grundlagen Seite Umkehrabbildungen Umkehrabbildungen •• Beispiel: Beispiel:Wie Wiekönnen könnenwir wirdie dieAbbildung Abbildung ff mit mit f(0) f(0)==b, b,f(1) f(1)==cc und und f(2) = a rückgängig machen? – Ganz einfach dadurch, dass wir f(2) = a rückgängig machen? – Ganz einfach dadurch, dass wir jedem jedemBild Bildsein seinUrbild Urbildzuordnen. zuordnen. Die Umkehrabbildung muss Die Umkehrabbildung muss bb auf auf 0, 0,cc auf auf 11 und und aa auf auf 22 abbilden. abbilden. •• Die DieUmkehrabbildung Umkehrabbildungvon von ff ist isteine eineAbbildung Abbildungvon von YY=={a, {a,b, b,c} c} inin –1 XX=={0, {0,1, 1,2}, 2},die diewir wirmit mit ff–1 bezeichnen. bezeichnen.Sie Sieist istdefiniert definiertdurch durch –1 –1 f–1 (a)==2, 2,ff–1(b) (b)==0, 0,ff–1(c) (c)==1. 1. f–1(a) •• Kurz: Kurz: Wenn Wenn wir wir mit mit ff die die Pfeile Pfeile von von links links nach nach rechts rechts durchlaufen, durchlaufen, –1 so durchlaufen wir mit f –1 die Pfeile von rechts nach links. so durchlaufen wir mit f die Pfeile von rechts nach links. © Dr. Zschiegner 2008 Seite 55 Kapitel 1: Grundlagen Beispiel Beispiel Beispiel: Beispiel:Die DieAbbildung Abbildungffvon vonRRininsich sichmit mit f(x) f(x)==2x+3 2x+3 ist istumkehrbar, umkehrbar,ihre ihreUmkehrabbildung Umkehrabbildungist ist f–1 f–1(x) (x)==½ ½(x (x––3), 3), denn denn –1 f–1 f–1(f(x)) (f(x))==ff–1(2x+3) (2x+3)==½ ½((2x+3) ((2x+3)––3) 3)==x.x. © Dr. Zschiegner 2008 Seite 56 Kapitel 1: Grundlagen Seite Aufgabe Aufgabe Die DieAbbildungen Abbildungen ff und und gg von vonRRininsich sichseien seiendurch durch f(x) f(x)==3x 3x und und g(x) = x − 1 definiert. g(x) = x − 1 definiert. (a) (a) Bilden BildenSie Siedie dieverkettete verketteteAbbildung Abbildung ffoog. g. (b) (b) Bestimmen BestimmenSie Siedie dieUmkehrabbildungen Umkehrabbildungenvon von f,f,ggund und ffoog. g. © Dr. Zschiegner 2008 Seite 57 Kapitel 1: Grundlagen 1.3 1.3Logik Logik © Dr. Zschiegner 2008 Seite 58 Kapitel 1: Grundlagen Seite Logik Logik •• Aussagen Aussagen •• Zusammengesetzte ZusammengesetzteAussagen Aussagen •• Wahrheitstafeln Wahrheitstafeln •• Allaussagen Allaussagen •• Existenzaussagen Existenzaussagen © Dr. Zschiegner 2008 Seite 59 Kapitel 1: Grundlagen Aussagen Aussagen •• Eine EineAussage Aussageist istein einsprachliches sprachlichesKonstrukt, Konstrukt,das dasprinzipiell prinzipiellfalsch falsch oder wahr ist. oder wahr ist. •• Beispiele Beispielefür fürAussagen: Aussagen: Alle Studenten Alle Studentensind sindintelligent. intelligent. Es Esgibt gibtunendlich unendlichviele vielePrimzahlen. Primzahlen. 2+2 = 5. 2+2 = 5. •• Keine KeineAussagen Aussagensind sindzum zumBeispiel: Beispiel: Guten Morgen! Guten Morgen! 5+3 5+3 © Dr. Zschiegner 2008 Seite 60 Kapitel 1: Grundlagen Seite Zusammengesetzte ZusammengesetzteAussagen Aussagen •• Wir Wirbezeichnen bezeichnenAussagen Aussagenmit mitGroßbuchstaben, Großbuchstaben,wie wieA, A,B, B,C. C. •• Aus Aus einer einer oder oder zwei zwei Aussagen Aussagen AA und und BB kann kann man man eine eine dritte dritte machen. Die wichtigsten „zusammengesetzten” Aussagen sind: machen. Die wichtigsten „zusammengesetzten” Aussagen sind: •• ¬A ¬A (nicht (nichtA) A) •• AA∨∨BB (A (A oder oder B) B) •• AA∧∧BB (A (A und und B) B) •• AA⇒ ⇒BB (wenn (wenn A, A,dann dannB) B) •• AA⇔ ⇔BB (A (A genau genaudann, dann,wenn wenn B) B) © Dr. Zschiegner 2008 Seite 61 Kapitel 1: Grundlagen Wahrheitstafeln Wahrheitstafeln Wie Wiekann kannman maneine einezusammengesetzte zusammengesetzteAussage Aussagebeschreiben? beschreiben? •• Wir Wir müssen müssen für für zusammengesetzte zusammengesetzte Aussagen Aussagen nur nur festlegen, festlegen, wann wann sie wahr und wann sie falsch sein sollen. sie wahr und wann sie falsch sein sollen. •• Das Das hängt hängt davon davon ab, ab, ob ob die die Aussagen Aussagen AA und und BB wahr wahr oder oder falsch falsch sind. sind. •• Dies Dieskönnen könnenwir wirmit mitHilfe Hilfevon vonWahrheitstafeln Wahrheitstafelnausdrücken. ausdrücken. © Dr. Zschiegner 2008 Seite 62 Kapitel 1: Grundlagen Seite AA∧∧BB(„A („A und und B“) B“) •• AA BB ww ww ww ff ff ff ww ff AA∧∧BB ww ff ff ff •• Wenn Wenn AA und und BB wahr wahrsind, sind,dann dannist ist AA∧∧BB wahr. wahr. Wenn Wenn AA wahr wahrund und BB falsch falschist, ist,dann dannist ist AA∧∧BB falsch. falsch. Wenn Wenn AA falsch falschund und BB wahr wahrist, ist,dann dannist ist AA∧∧BB falsch. falsch. Wenn A und B falsch sind, dann ist A ∧ B falsch. Wenn A und B falsch sind, dann ist A ∧ B falsch. •• Beispiel: Beispiel:Die DieAussage Aussage (2+2=5) (2+2=5)∧∧(5 (5 ist isteine einePrimzahl) Primzahl) ist istfalsch. falsch. © Dr. Zschiegner 2008 Seite 63 Kapitel 1: Grundlagen AA∨∨ BB(„A („A oder oder B“) B“) •• AA BB ww ww ww ff ff ff ww ff AA∨∨BB ww ww ww ff •• Wenn Wenn AA und und BB wahr wahrsind, sind,dann dannist ist AA∨∨BB wahr. wahr. Wenn A wahr und B falsch ist, dann ist A ∨ Wenn A wahr und B falsch ist, dann ist A ∨BB wahr. wahr. Wenn Wenn AA falsch falschund und BB wahr wahrist, ist,dann dannist ist AA∨∨BB wahr. wahr. Wenn A und B falsch sind, dann ist A ∨ B falsch. Wenn A und B falsch sind, dann ist A ∨ B falsch. •• Beispiel: Beispiel:Die DieAussage Aussage (2+2=5) (2+2=5)∨∨(5 (5 ist isteine einePrimzahl) Primzahl) ist istwahr. wahr. © Dr. Zschiegner 2008 Seite 64 Kapitel 1: Grundlagen Seite ¬A ¬A („nicht („nicht A“) A“) AA ¬A ¬A ww ff ff ww •• Das Das bedeutet: bedeutet: ¬A ¬A ist ist genau genau dann dann eine eine wahre wahre Aussage, Aussage, wenn wenn AA falsch falschist. ist. •• Beispiel: Beispiel:¬(2+2=5) ¬(2+2=5) ist isteine einewahre wahreAussage. Aussage. © Dr. Zschiegner 2008 Seite 65 Kapitel 1: Grundlagen Aufgaben Aufgaben Bilden BildenSie Siedie dieNegation Negationder derfolgenden folgendenAussagen Aussagenund undentscheiden entscheidenSie, Sie, ob die gegebenen Aussagen oder die jeweiligen Negationen wahr sind. ob die gegebenen Aussagen oder die jeweiligen Negationen wahr sind. (a) (a)Heute Heuteist istMittwoch. Mittwoch. (b) (b)88··77==55. 55. (c) (c)(3 (3++44==7) 7)∧∧(3 (3··44>>12). 12). (d) (d)(2+2=5) (2+2=5)∨∨¬(5 ¬(5 ist isteine einePrimzahl). Primzahl). © Dr. Zschiegner 2008 Seite 66 Kapitel 1: Grundlagen Seite AA⇒ ⇒ BB(„wenn („wenn A, A,dann dann B“) B“) AA BB ww ww ww ff ff ff ww ff AA⇒ ⇒BB ww ff ww ww •• Wenn Wenn AA und und BB wahr wahrsind, sind,dann dannist ist AA⇒ ⇒BB eine einewahre wahreAussage. Aussage. Wenn Wenn AA wahr wahrund und BB falsch falschist, ist,dann dannist ist AA⇒ ⇒BB falsch. falsch. Wenn Wenn AA falsch falschund und BB wahr wahrist, ist,dann dannist ist AA⇒ ⇒BB wahr. wahr. Wenn A und B falsch sind, dann ist A ⇒ B eine Wenn A und B falsch sind, dann ist A ⇒ B einewahre wahreAussage. Aussage. •• Beispiel: Beispiel:Die DieAussage Aussage (2+2=5) (2+2=5)⇒ ⇒(5 (5 ist isteine einePrimzahl) Primzahl) ist istwahr. wahr. © Dr. Zschiegner 2008 Seite 67 Kapitel 1: Grundlagen AA⇔ ⇔ BB („A („A genau genaudann, dann,wenn wenn B“) B“) AA BB ww ww ww ff ff ff ww ff AA⇔ ⇔BB ww ff ff ww •• AA⇔ ⇔BB ist istgenau genaudann danneine einewahre wahreAussage, Aussage,wenn wenn AA und und BB beide beide wahr oder beide falsch sind. wahr oder beide falsch sind. •• Beispiel: Beispiel:Die DieAussage Aussage (2+2=5) (2+2=5)⇔ ⇔(5 (5 ist isteine einePrimzahl) Primzahl) ist isteine eine falsche falscheAussage, Aussage,aber aberdie dieAussage Aussage (2+2=5) (2+2=5)⇔ ⇔(6 (6 ist isteine einePrimzahl) Primzahl) ist isteine einewahre wahreAussage. Aussage. © Dr. Zschiegner 2008 Seite 68 Kapitel 1: Grundlagen Seite Aussagen: Aussagen: Bemerkungen Bemerkungen •• Wenn Wennzwei zweiAussagen Aussagenden dengleichen gleichenWahrheitswert Wahrheitswerthaben haben(also (alsobeide beide wahr oder beide falsch sind), so schreiben wir A = B. (Man könnte wahr oder beide falsch sind), so schreiben wir A = B. (Man könnte auch auch AA⇔ ⇔BB schreiben.) schreiben.) •• Bemerkung. Bemerkung.Obige ObigeFestlegungen Festlegungenerscheinen erscheinenzum zumTeil Teilwillkürlich. willkürlich. Aber Aberso sosind sinddie dieSymbole Symboleund undder derSprachgebrauch Sprachgebrauchininder der Mathematik Mathematikfestgelegt! festgelegt!Dass Dassdies diesso sosinnvoll sinnvollist, ist,wird wirdsich sichnoch noch herausstellen… herausstellen… © Dr. Zschiegner 2008 Seite 69 Kapitel 1: Grundlagen Sätze Sätze •• Wahrheitstafeln Wahrheitstafelndienen dienennicht nichtnur nurder derDefinition Definitionvon vonAussagen, Aussagen, sondern können auch dazu verwendet werden, Sätze sondern können auch dazu verwendet werden, Sätzezu zubeweisen. beweisen. •• Was Wasist istein einmathematischer mathematischerSatz? Satz? Ein mathematischer Satz ist Ein mathematischer Satz isteine einezusammengesetzte zusammengesetzteAussage, Aussage,die die immer wahr ist. immer wahr ist. Das Dasheißt, heißt,dass dasssie sieunabhängig unabhängigvon vonder derVerteilung Verteilungder der Wahrheitswerte Wahrheitswerteder derEinzelaussagen Einzelaussagenwahr wahrist. ist. •• Ein Einmathematischer mathematischerSatz Satzbesteht bestehtimmer immeraus auseiner einerVoraussetzung Voraussetzung und undeiner einerBehauptung. Behauptung. Das Dasheißt: heißt:Jeder JederSatz Satzist isteine eine„Wenn-dann-Aussage“. „Wenn-dann-Aussage“. © Dr. Zschiegner 2008 Seite 70 Kapitel 1: Grundlagen Seite Ein Eineinfacher einfacherSatz Satz Satz. Satz.Für Füralle alleAussagen Aussagen AA und und BB gilt: gilt: (A (A∧∧B) B)⇒ ⇒A. A. „Gelten” „Gelten”bedeutet, bedeutet,dass dassdie dieGesamtaussage Gesamtaussagestets stetswahr wahrist, ist,unabunabhängig hängigdavon, davon,ob obdie dieAussagen Aussagen AA und und BB wahr wahroder oderfalsch falschsind. sind. Beweis. Beweis. AA BB AA∧∧BB (A (A∧∧B) B)⇒ ⇒AA ww ww ww ww ww ff ff ww ff ff ff ff ww ww ff ww © Dr. Zschiegner 2008 Seite 71 Kapitel 1: Grundlagen Die Die de de Morganschen Morganschen Gesetze Gesetze 1.3.1 1.3.1Satz Satz(Augustus (Augustusde deMorgan). Morgan).Seien Seien AA und und BB Aussagen. Aussagen.Dann Dann gilt gilt (a) (a) ¬(A ¬(A∧∧B) B)==¬A ¬A∨∨¬B ¬B(erstes (erstesde deMorgansches MorganschesGesetz). Gesetz). (b) (b) ¬(A ¬(A∨∨B) B)==¬A ¬A∧∧¬B ¬B(zweites (zweitesde deMorgansches MorganschesGesetz). Gesetz). Beweisidee. Beweisidee.(a) (a)Wir Wirzeigen zeigendiese dieseBehauptung Behauptungdadurch, dadurch,dass dasswir wir zeigen, dass für jede Belegung der Wahrheitswerte von A und zeigen, dass für jede Belegung der Wahrheitswerte von A und BB die diebeiden beidenSeiten Seiten ¬(A ¬(A∧∧B) B) und und ¬A ¬A∨∨¬B ¬B stets stetsden dengleichen gleichen Wahrheitswert haben. Wahrheitswert haben. © Dr. Zschiegner 2008 Seite 72 Kapitel 1: Grundlagen Seite Beweis Beweisdes desersten erstende deMorganschen MorganschenGesetzes Gesetzes Wahrheitstafel Wahrheitstafelfür für ¬(A ¬(A∧∧B) B) und und ¬A ¬A∨∨¬B ¬B AA ww ww ff ff BB ww ff ww ff ¬(A ¬(A∧∧B) B) ff ww ww ww ¬A ¬A ff ff ww ww ¬B ¬B ff ww ff ww ¬A ¬A∨∨¬B ¬B ff ww ww ww Die Diebeiden beidenSeiten Seitenhaben habengenau genauan anden dengleichen gleichenStellen Stellen ww und und ff stehen; stehen;also alsosind sinddie dieAussagen Aussagengleich. gleich. © Dr. Zschiegner 2008 Seite 73 Kapitel 1: Grundlagen Beweis Beweisdes deszweiten zweitende deMorganschen MorganschenGesetzes Gesetzes Wahrheitstafel Wahrheitstafelfür für ¬(A ¬(A∨∨B) B) und und ¬A ¬A∧∧¬B: ¬B: AA ww ww ff ff BB ww ff ww ff ¬(A ¬(A∨∨B) B) ff ff ff ww ¬A ¬A ff ff ww ww ¬B ¬B ff ww ff ww ¬A ¬A∧∧¬B ¬B ff ff ff ww Die Diebeiden beidenSeiten Seitenhaben habengenau genauan anden dengleichen gleichenStellen Stellen ww und und ff stehen; stehen;also alsosind sinddie dieAussagen Aussagengleich. gleich. © Dr. Zschiegner 2008 Seite 74 Kapitel 1: Grundlagen Seite Aufgaben Aufgaben Beweisen BeweisenSie Siemit mitHilfe Hilfeeiner einerWahrheitstafel Wahrheitstafeldie dieAussagen Aussagen (a) (a)AA∧∧(A (A∨∨B) B)==A, A, (b) (b)(A (A∨∨B) B)∧∧CC==(A (A∧∧C) C)∨∨(B (B∧∧C), C), (c) (c)AA⇒ ⇒BB==(¬A) (¬A)∨∨B, B, (d) (d)AA⇒ ⇒BB==(¬B) (¬B)⇒ ⇒(¬A) (¬A) (Prinzip (Prinzipdes desWiderspruchsbeweises). Widerspruchsbeweises). © Dr. Zschiegner 2008 Seite 75 Kapitel 1: Grundlagen Exkurs: Exkurs:Widerspruchsbeweis Widerspruchsbeweis Beim BeimWiderspruchsbeweis Widerspruchsbeweisnimmt nimmt man manzunächst zunächstdas dasGegenteil Gegenteilvon von dem deman, an,was wasman manbeweisen beweisenmöchte. möchte. Durch logisches Schließen gelangt Durch logisches Schließen gelangt man manzu zueinem einemWiderspruch. Widerspruch. Beispiel: Beispiel:Behauptung: Behauptung:Man Man kann das Schachbrett, von kann das Schachbrett, vondem dem zwei zweiweiße weißeEckfelder Eckfelderentfernt entfernt sind, sind,nicht nichtmit mitDominosteinen, Dominosteinen, die zwei Schachfelder die zwei Schachfeldergroß großsind, sind, überdecken. überdecken. © Dr. Zschiegner 2008 Seite 76 Kapitel 1: Grundlagen Seite © Dr. Zschiegner 2008 Seite 77 Kapitel 1: Grundlagen Allaussagen Allaussagen Allaussagen: Allaussagen:Aussagen Aussagenüber überalle alleElemente Elementeeiner einerMenge. Menge. Beispiel: Beispiel:Alle AllePrimzahlen Primzahlen>>22sind sindungerade. ungerade. In jedem Dreieck schneiden sich die In jedem Dreieck schneiden sich dieMittellote Mittelloteinineinem einemPunkt. Punkt. Formal Formalschreiben schreibenwir wirdafür dafür Für alle x gilt ... Für alle x gilt ... ∀∀xx... ... Beispiele: Beispiele: Für Füralle alleDreiecke Dreieckegilt: gilt:Die DieWinkelsumme Winkelsummeist ist180° 180° Sei Sei M M=={1, {1,3, 3,5, 5,7}. 7}.Dann Danngilt: gilt: Für Füralle alle m m∈∈M M ist ist m m eine eineungerade ungerade Zahl. Zahl. © Dr. Zschiegner 2008 Seite 78 Kapitel 1: Grundlagen Seite Allaussagen: Allaussagen:Bemerkungen Bemerkungen 1. 1.Es Esgibt gibtkeinen keinenlogischen logischenUnterschied Unterschiedzwischen zwischen„Für „Füralle alleElemente Elemente gilt ...“ und „für jedes Element gilt ...“. gilt ...“ und „für jedes Element gilt ...“. Sprachlich Sprachlichist istmanchmal manchmaldas daseine, eine,manchmal manchmaldas dasandere anderebesser. besser. 2. 2.Eine EineAllaussage Allaussageist isteine einelange langeund-Aussage. und-Aussage. Beispiel: Beispiel:Sei Sei M M=={1, {1,3, 3,5, 5,7}. 7}.Dann Danngilt: gilt: Für Füralle alle m m∈∈M M ist ist m m eine eine ungerade Zahl. ungerade Zahl. Stattdessen Stattdessenkann kannman manauch auchsagen sagenund undschreiben: schreiben: (1 (1 ist istungerade) ungerade)∧∧(3 (3 ist istungerade) ungerade)∧∧(5 (5 ist istungerade) ungerade) ∧∧(7 (7 ist istungerade). ungerade). © Dr. Zschiegner 2008 Seite 79 Kapitel 1: Grundlagen Existenzaussagen Existenzaussagen Existenzaussage: Existenzaussage:Es Esgibt gibtmindestens mindestensein einElement Elementder derbetreffenden betreffenden Menge, das eine gewisse Eigenschaft hat. Menge, das eine gewisse Eigenschaft hat. Beispiele: Beispiele:(a) (a)Es Esgibt gibteine einegerade geradePrimzahl. Primzahl. (b) Sei M = {1, 4, 9, 16}. Dann gilt (b) Sei M = {1, 4, 9, 16}. Dann gilt ∃∃ m m∈∈M: M:m m ist istgerade. gerade. Jede JedeExistenzaussage Existenzaussageist isteine einesehr sehrlange langeoder-Aussage. oder-Aussage.Statt Statt ∃∃ m m∈∈M, M,das dasgerade geradeist ist kann kannman manauch auchsagen: sagen: (1 (1 ist istgerade) gerade)∨∨(4 (4 ist istgerade) gerade)∨∨(9 (9 ist istgerade) gerade)∨∨(16 (16 ist istgerade). gerade). © Dr. Zschiegner 2008 Seite 80 Kapitel 1: Grundlagen Seite Verneinung Verneinungvon vonAllAll-und undExistenzaussagen Existenzaussagen 1.3.2 1.3.2Satz. Satz.(a) (a)Die DieNegation Negationeiner einerAllaussage Allaussageist isteine eine Existenzaussage. Genauer gilt: Existenzaussage. Genauer gilt: ¬(∀ ¬(∀xx gilt gilt...) ...)==∃∃x,x,für fürdas dasnicht nichtgilt gilt... ... (b) (b)Die DieNegation Negationeiner einerExistenzaussage Existenzaussageist isteine eineAllaussage. Allaussage. Genauer Genauergilt: gilt: ¬(∃ ¬(∃x,x,für fürdas dasgilt gilt))==∀∀xx gilt giltnicht nicht... ... Beispiele: Beispiele:(a) (a)Alle AlleSchwäne Schwänesind sindweiß weiß Negation: Es gibt einen nichtweißen Negation: Es gibt einen nichtweißenSchwan. Schwan. (b) (b)Es Esgibt gibteinen einendummen dummenStudenten Studenten Negation: Negation:Alle AlleStudenten Studentensind sindintelligent. intelligent. © Dr. Zschiegner 2008 Seite 81 Kapitel 1: Grundlagen Aufgaben Aufgaben Bilden BildenSie Siedie dieNegation Negationder derfolgenden folgendenAllAll-bzw. bzw.Existenzaussagen Existenzaussagenund und entscheiden Sie, ob die gegebenen Aussagen oder die jeweiligen entscheiden Sie, ob die gegebenen Aussagen oder die jeweiligen Negationen Negationenwahr wahrsind. sind. (a) (a)Jede JedePrimzahl Primzahlist istungerade. ungerade. (b) (b)Für Füralle allenn∈∈NNgilt: gilt:2n 2n++11ist istungerade. ungerade. (c) (c)Es Esgibt gibteine einenatürliche natürlicheZahl, Zahl,deren derenQuadrat Quadratgleich gleich169 169ist. ist. (d) (d)Jede JedeGerade Geradetrifft trifftden denEinheitskreis Einheitskreisininmindestens mindestenseinem einemPunkt. Punkt. (e) (e)Keine KeineGerade Geradetrifft trifftden denEinheitskreis Einheitskreisininmehr mehrals alszwei zweiPunkten. Punkten. © Dr. Zschiegner 2008 Seite 82 Kapitel 1: Grundlagen Seite Aufgabe Aufgabe Frau FrauMüller Müllerkündigt kündigtan: an:„Für „Fürheute heuteAbend Abendhabe habeich ichFamilie FamilieMeier Meierzu zu uns unseingeladen.“ eingeladen.“Herr HerrMüller Müllerfragt fragtbestürzt: bestürzt:„Kommt „Kommtetwa etwadie dieganze ganze Familie, Familie,also alsoHerr Herrund undFrau FrauMeier Meiermit mitihren ihrenSöhnen SöhnenAndreas, Andreas,Bernd Bernd und Christian?“ Frau Müller möchte ihren Mann zum logischen und Christian?“ Frau Müller möchte ihren Mann zum logischenDenken Denken anreizen und antwortet: „Wenn Herr Meier kommt, dann bringt er anreizen und antwortet: „Wenn Herr Meier kommt, dann bringt erauch auch seine seineFrau Fraumit. mit.Es Eskommt kommtmindestens mindestenseiner einerder derSöhne SöhneBernd Berndund und Christian. Christian.Entweder Entwederkommt kommtFrau FrauMeier Meieroder oderAndreas. Andreas.Andreas Andreasund und Christian kommen entweder beide oder aber beide nicht. Und wenn Christian kommen entweder beide oder aber beide nicht. Und wenn Bernd Berndkommt, kommt,dann dannkommen kommenauch auchChristian Christianund undHerr HerrMeier. Meier.−−Alles Alles klar?“ klar?“Wer Werkommt kommtabends abendszu zuBesuch? Besuch? © Dr. Zschiegner 2008 Seite 83 Kapitel 1: Grundlagen 1.4 1.4Beweisen Beweisenmit mitvollständiger vollständigerInduktion Induktion © Dr. Zschiegner 2008 Seite 84 Kapitel 1: Grundlagen Seite Inhalt Inhalt 1.4.1 1.4.1Das DasPrinzip Prinzip A(n) A(n)⇒ ⇒A(n+1) A(n+1) 1.4.2 1.4.2Anwendungen Anwendungen 11++22++33++... ...++nn==?? 1.4.3 1.4.3Fibonacci-Zahlen Fibonacci-Zahlen 1, 1,1, 1,2, 2,3, 3,5, 5,8,13, 8,13,21, 21,... ... © Dr. Zschiegner 2008 Seite 85 Kapitel 1: Grundlagen 1.4.1 1.4.1 Das Das Prinzip Prinzip •• Ziel: Ziel:In Inder derMathematik Mathematikmacht machtman manin inder derRegel RegelAussagen Aussagenüber über unendlich viele Objekte (alle Zahlen, alle Dreiecke usw.) unendlich viele Objekte (alle Zahlen, alle Dreiecke usw.) •• Solche SolcheAussagen Aussagenkann kannman manprinzipiell prinzipiellnicht nichtdadurch dadurchklären klären („beweisen“), („beweisen“),dass dassman manalle alleFälle Fälleeinzeln einzelnausprobiert. ausprobiert.Man Manmuß muß die dieAussage Aussagesozusagen sozusagen„auf „aufeinen einenSchlag“ Schlag“erledigen. erledigen.Dazu Dazu dient die (vollständige, mathematische) Induktion. dient die (vollständige, mathematische) Induktion. •• Bemerkung: Bemerkung:Unter Unter„Induktion“ „Induktion“versteht verstehtman man(im (imGegensatz Gegensatzzur zur „Deduktion“ „Deduktion“eigentlich eigentlichdas das––logisch logischunzulässige unzulässige––Schließen Schließenvon von Einzelfällen Einzelfällenauf aufalle alleFälle. Fälle.Die Diemathematische mathematischeInduktion Induktionist istein ein Werkzeug, mit dem man das sauber machen kann. Werkzeug, mit dem man das sauber machen kann. © Dr. Zschiegner 2008 Seite 86 Kapitel 1: Grundlagen Seite Zum ZumPrinzip Prinzipder dervollständigen vollständigenInduktion Induktion © Dr. Zschiegner 2008 Seite 87 Kapitel 1: Grundlagen Das DasPrinzip Prinzipder dervollständigen vollständigenInduktion Induktion Prinzip Prinzip der der vollständigen vollständigen Induktion. Induktion. Sei Sei AA eine eine Aussage Aussage oder oder eine Eigenschaft, die von einer natürlichen Zahl n abhängt. eine Eigenschaft, die von einer natürlichen Zahl n abhängt.Wir Wir schreiben schreibenauch auch A(n). A(n). Wenn Wennwir wirwissen, wissen,dass dassfolgendes folgendesgilt: gilt: (1) (1) Induktionsbasis Induktionsbasis (Induktionsverankerung): (Induktionsverankerung): Die Die Aussage Aussage AA gilt giltim imFall Fall nn==11 (das (dasheißt, heißt,es esgilt gilt A(1)), A(1)), (2) (2) Induktionsschritt: Induktionsschritt: Für Für jede jede natürliche natürliche Zahl Zahl nn ≥≥ 11 folgt folgt aus aus A(n) die Aussage A(n+1), A(n) die Aussage A(n+1), dann danngilt giltdie dieAussage Aussage AA für füralle allenatürlichen natürlichenZahlen Zahlen ≥≥1. 1. © Dr. Zschiegner 2008 Seite 88 Kapitel 1: Grundlagen Seite Erläuterung Erläuterung Bedeutung Bedeutungder dervollständigen vollständigenInduktion: Induktion:Um Umeine eineAussage Aussageüber über unendlich unendlichviele vieleObjekte Objektenachzuweisen, nachzuweisen,muss mussman mannur nurzwei zwei Aussagen Aussagenbeweisen: beweisen: Induktionsbasis: Induktionsbasis:A(1) A(1) Induktionsschritt: Induktionsschritt:A(n) A(n)⇒ ⇒A(n+1) A(n+1) Man nennt A(n) auch die Induktionsvoraussetzung. Man nennt A(n) auch die Induktionsvoraussetzung. Die Diehinter hinterdiesem diesemPrinzip Prinzipstehende stehende“Philosophie” “Philosophie”ist istdie, die,dass dassman maninin objektiv objektivkontrollierbarer kontrollierbarerWeise Weiseüber übereine eineUnendlichkeit Unendlichkeit(“alle” (“alle” natürlichen natürlichenZahlen) Zahlen)sprechen sprechenkann. kann.Die DieBedeutung Bedeutungdieses diesesPrinzips, Prinzips, wurde zwischen 1860 und 1920 u.a. von Moritz Pasch (Professor wurde zwischen 1860 und 1920 u.a. von Moritz Pasch (Professorinin Gießen) Gießen)und undGiuseppe GiuseppePeano Peano(Professor (ProfessorininTurin) Turin)entdeckt. entdeckt. © Dr. Zschiegner 2008 Seite 89 Kapitel 1: Grundlagen Aussagen Aussagen A(n): A(n):4n 4n ist isteine einegerade geradeZahl Zahl 2 A(n): A(n):nn2 ist isteine einegerade geradeZahl Zahl A(n): A(n):nn ist isteine einePrimzahl Primzahl A(n): A(n):Die DieAnzahl Anzahlder derSitzordnungen Sitzordnungenvon von nn Studierenden Studierendenauf auf nn Stühlen Stühlenist ist n! n!(= (=n⋅(n–1)⋅...⋅2⋅1, n⋅(n–1)⋅...⋅2⋅1,sprich sprich „n „n Fakultät”) Fakultät”) A(n): A(n):nn geradlinige geradlinigeStraßen Straßenhaben habenhöchstens höchstens nn Kreuzungen Kreuzungen A(n): A(n):Wenn Wenn nn Computer Computerzu zujejezweien zweiendurch durcheine eineLeitung Leitungverbunden verbunden werden, werden,so sobraucht brauchtman mangenau genau n(n–1)/2 n(n–1)/2 Leitungen Leitungen © Dr. Zschiegner 2008 Seite 90 Kapitel 1: Grundlagen Seite 1.4.2 1.4.2Anwendungen Anwendungen Problem Problem(C.F. (C.F.Gauß): Gauß):1+2+3 1+2+3+...+ +...+100 100==??? ??? 1.4.2.1 1.4.2.1Satz. Satz.Für Fürjede jedenatürliche natürlicheZahl Zahl nn≥≥11 gilt: gilt: 1+2+... 1+2+...++nn==n(n+1)/2. n(n+1)/2. In InWorten: Worten:Die DieSumme Summeder derersten ersten nn positiven positivenganzen ganzenZahlen Zahlenist ist gleich (n+1)n/2. gleich (n+1)n/2. Konsequenz: Konsequenz:Man Mankann kanndie dieSumme Summe1+2+3+...+n 1+2+3+...+n ganz ganzeinfach einfach ausrechnen, und es passieren kaum Rechenfehler. ausrechnen, und es passieren kaum Rechenfehler. © Dr. Zschiegner 2008 Seite 91 Kapitel 1: Grundlagen Dreieckszahlen Dreieckszahlen Definition. Definition. Die Die Zahlen Zahlen der der Form Form (n+1)n/2, (n+1)n/2, also also die die Zahlen Zahlen 1, 1, 3, 3, 6, 6, 10, 15, ... heißen Dreieckszahlen. 10, 15, ... heißen Dreieckszahlen. Man Man kann kann Satz Satz 1.4.2.1 1.4.2.1 also also auch auch so so ausdrücken: ausdrücken: Die Die Summe Summe der der ersten n positiven ganzen Zahlen ist gleich der n-ten Dreieckszahl. ersten n positiven ganzen Zahlen ist gleich der n-ten Dreieckszahl. © Dr. Zschiegner 2008 Seite 92 Kapitel 1: Grundlagen Seite Beweis Beweis(durch (durchInduktion) Induktion) Beweis Beweisdurch durchInduktion Induktionnach nach n. n. Die DieAussage Aussage A(n) A(n) sei seidie dieAussage Aussagedes desSatzes, Satzes,also: also: A(n): A(n):1+2+3 1+2+3+...+ +...+nn==n(n+1)/2. n(n+1)/2. Sowohl Sowohl bei bei der der Induktionsbasis Induktionsbasis als als auch auch beim beim Induktionsschritt Induktionsschritt zeigen wir, dass in der entsprechenden Gleichung links zeigen wir, dass in der entsprechenden Gleichung links und und rechts rechts das dasGleiche Gleichesteht. steht. Induktionsbasis: Induktionsbasis:Sei Sei nn==1. 1.Dann Dannsteht stehtauf aufder derlinken linkenSeite Seitenur nurder der Summand 1, und auf der rechten Seite steht 2⋅1/2, also ebenfalls Summand 1, und auf der rechten Seite steht 2⋅1/2, also ebenfalls 1. 1.Also Alsogilt giltA(1) A(1) © Dr. Zschiegner 2008 Seite 93 Kapitel 1: Grundlagen Induktionsschritt Induktionsschritt Induktionsschritt: Induktionsschritt:Sei Sei nn eine einenatürliche natürlicheZahl Zahl ≥≥1, 1,und undsei seidie die Aussage richtig für n. Wir müssen A(n+1) beweisen, das heißt, Aussage richtig für n. Wir müssen A(n+1) beweisen, das heißt,die die Summe Summe 1+2+3+... 1+2+3+...+(n–1) +(n–1)++nn++(n+1) (n+1) berechnen. berechnen. Wir Wirspalten spaltenwir wirdiese dieseSumme Summeauf: auf: 1+2+3+... 1+2+3+...+(n–1) +(n–1)++nn++(n+1) (n+1) ==[1+2+3+... +(n–1) + n] + [1+2+3+... +(n–1) + n] +(n+1) (n+1) == n(n+1)/2 + (n+1) (nach n(n+1)/2 + (n+1) (nachInduktion) Induktion) ==[n(n+1) + 2(n+1)]/2 = (n+2)(n+1)/2. [n(n+1) + 2(n+1)]/2 = (n+2)(n+1)/2. Insgesamt Insgesamthaben habenwir wirdie dieAussage Aussage A(n+1) A(n+1) bewiesen. bewiesen. Somit gilt der Satz. Somit gilt der Satz. © Dr. Zschiegner 2008 Seite 94 Kapitel 1: Grundlagen Seite Der DerTrick Trickvon vonGauß Gauß Gauß Gaußhat hatdie dieSumme Summe1+2+3+...+100 1+2+3+...+100nicht nichtso sobestimmt, bestimmt,sondern sondernmit mit folgendem folgendemgenialen genialenTrick: Trick: 11 ++ nn ++ 22 ++ 33 ++ ++ n–1 n–1++ n–2 n–2++ ... ... ... ... ++n–2 n–2 ++n–1 n–1++ ++ 33 ++ 22 ++ nn 11 ==n+1 n+1++ n+1 n+1++ n+1 n+1++ ... ... ++n+1 n+1 ++n+1 n+1++ n+1 n+1 ==n(n+1). n(n+1). Also Alsogilt gilt 1+2+3+...+n 1+2+3+...+n==n(n+1)/2. n(n+1)/2. © Dr. Zschiegner 2008 Seite 95 Kapitel 1: Grundlagen Summe Summeder derungeraden ungeradenZahlen Zahlen 1.4.2.2 1.4.2.2Satz. Satz.Für Fürjede jedenatürliche natürlicheZahl Zahl nn≥≥11 gilt: gilt: 2 2 . 1+3+5 + ... + (2n–1) = n 1+3+5 + ... + (2n–1) = n . In InWorten: Worten:Die DieSumme Summeder derersten ersten nn ungeraden ungeradenZahlen Zahlenist istgleich gleichder der n-ten Quadratzahl. n-ten Quadratzahl. Beispiele: Beispiele:(a) (a)11++33++55==99 (b) (b)11++33++55++... ...++1999 1999==1.000.000 1.000.000 © Dr. Zschiegner 2008 Seite 96 Kapitel 1: Grundlagen Seite „Beweis“ „Beweis“ohne ohneWorte Worte © Dr. Zschiegner 2008 Seite 97 Kapitel 1: Grundlagen Beweis Beweis Beweis Beweisdurch durchInduktion Induktionnach nach n. n. Induktionsbasis: Induktionsbasis:Sei Sei nn==1. 1.Dann Dann steht stehtauf aufder derlinken linkenSeite Seitenur nurder der 2 Summand Summand 1, 1,und undauf aufder derrechten rechtenSeite Seitesteht steht 112==1. 1.Somit Somitgilt gilt A(1). A(1). Induktionsschritt: Sei n eine natürliche Zahl mit n ≥ 1, und es gelte Induktionsschritt: Sei n eine natürliche Zahl mit n ≥ 1, und es gelte A(n). A(n).Wir Wirmüssen müssen A(n+1) A(n+1) nachweisen. nachweisen. Wir beginnen mit der linken Wir beginnen mit der linkenSeite Seitevon von A(n+1) A(n+1) und undformen formendiese dieseso so lange langeum, um,bis biswir wirdie dierechte rechteSeite Seitevon von A(n+1) A(n+1) erhalten: erhalten: 1+3+5+ 1+3+5+... ...++(2n–1) (2n–1)++(2n+1) (2n+1)==[1+3+5+ [1+3+5+... ...++(2n–1)] (2n–1)]++(2n+1) (2n+1) 2 ==nn2++(2n+1) (nach Induktion) (2n+1) (nach Induktion) 2 ==nn22++2n + 1 2n + 1==(n+1) (n+1)2.. Somit Somitgilt gilt A(n+1), A(n+1),und unddamit damitist istdie dieAussage Aussagebewiesen. bewiesen. © Dr. Zschiegner 2008 Seite 98 Kapitel 1: Grundlagen Seite Die DieBernoullische BernoullischeUngleichung Ungleichung 1.4.2.3 1.4.2.3Satz. Satz.Für Fürjede jedenat. nat.Zahl Zahl nn und undjede jedereelle reelleZahl Zahl xx≥≥-1 -1gilt gilt n n ≥ 1 + nx. (1+x) (1+x) ≥ 1 + nx. Beweis Beweisdurch durchInduktion Induktionnach nach n. n. Induktionsbasis: Sei n = 1. Dann Induktionsbasis: Sei n = 1. Dannist istlinke linkeSeite Seite==1+x 1+x==rechte rechteSeite; Seite; insbesondere insbesondereist ist linke linkeSeite Seite≥≥rechte rechteSeite. Seite. Induktionsschritt: Sei n eine natürliche Induktionsschritt: Sei n eine natürlicheZahl Zahlmit mit nn≥≥1, 1,und undsei seidie die Behauptung Behauptungrichtig richtigfür für n. n.Damit Damitfolgt folgt n+1 n (1+x) (1+x)n⋅(1+x) ⋅(1+x) (1+x)n+1==(1+x) ≥≥(1 (1++nx) nx)⋅(1+x) ⋅(1+x) (nach (nachInduktion) Induktion) 2 ==11++nx nx++xx++nx nx2≥≥11++nx nx++xx==11++(n+1)x. (n+1)x. Damit Damitist istder derInduktionsschritt Induktionsschrittbewiesen, bewiesen,und unddamit damitgilt giltder derSatz. Satz. © Dr. Zschiegner 2008 Seite 99 Kapitel 1: Grundlagen Aufgaben Aufgaben Beweisen BeweisenSie Siedurch durchInduktion Induktionnach nach n: n: (a)3 (a)3++77++11 11++......++(4n (4n––1) 1)==nn(2n (2n++1). 1). (b)2 (b)2++44++66++......++2n 2n==nn(n+1). (n+1). n n+1 (c) (c) 11++22++44++... ...++22n==22n+1––1. 1. 2 2 2 2 (d) (d) 112++222++332++... ...++nn2== n ⋅ (n + 1) ⋅ (2n + 1) 6 .. 3 3 3 2 (e) (e) 113++223++......++nn3==(1 (1++22++33++......++n) n)2.. © Dr. Zschiegner 2008 Seite 100 Kapitel 1: Grundlagen Seite Aufgabe Aufgabe Ein Einbekanntes bekanntesmathematisches mathematischesSpiel Spielist istder der„Turm „Turmvon vonHanoi“. Hanoi“. Auf Aufeinem einemvon vondrei dreiStäben Stäbensitzen sitzen nn Scheiben, Scheiben,die diekleinste kleinsteoben, oben,die die größte größteunten. unten.Die DieAufgabe Aufgabebesteht bestehtdarin, darin,diese dieseScheiben Scheibenauf aufeinen einender der anderen Stäbe zu bringen, wobei folgende Regeln zu beachten sind: anderen Stäbe zu bringen, wobei folgende Regeln zu beachten sind: 1. 1.In Injedem jedemSchritt Schrittdarf darfnur nureine eineScheibe Scheibebewegt bewegtwerden. werden. 2. 2.Nie Niedarf darfeine einegrößere größereScheibe Scheibeauf aufeiner einerkleineren kleinerenliegen. liegen. Zeigen ZeigenSie Siemit mitvollständiger vollständigerInduktion, Induktion,dass dassman mandiese dieseAufgabe Aufgabemit mit n 22n––11 Schritten lösen kann. Schritten lösen kann. © Dr. Zschiegner 2008 Seite 101 Kapitel 1: Grundlagen Der DerTurm Turmvon vonHanoi Hanoi © Dr. Zschiegner 2008 Seite 102 Kapitel 1: Grundlagen Seite Lösungsbeispiel Lösungsbeispielfür für44Scheiben Scheiben © Dr. Zschiegner 2008 Seite 103 Kapitel 1: Grundlagen Der DerTurm Turmvon vonIonah Ionahim imMathematikum Mathematikum © Dr. Zschiegner 2008 Seite 104 Kapitel 1: Grundlagen Seite 1.4.3 1.4.3Die DieFibonacci-Zahlen Fibonacci-Zahlen Fibonacci Fibonacci(= (=Leonardo Leonardovon vonPisa) Pisa)stellte stellteum um1200 1200die dieAufgabe: Aufgabe: •• Kaninchen Kaninchen(jedenfalls (jedenfallsmathematische) mathematische)vermehren vermehrensich sichnach nach folgenden Regeln: folgenden Regeln: –– Jedes JedesKaninchenpaar Kaninchenpaarbraucht brauchtnach nachseiner seinerGeburt Geburtzwei zweiMonate, Monate, bis es geschlechtsreif ist. bis es geschlechtsreif ist. –– Von Vonda daan angebiert gebiertes esininjedem jedemMonat Monatein einneues neuesPaar Paar –– Alle AlleKaninchen Kaninchenleben lebenewig. ewig. © Dr. Zschiegner 2008 Seite 105 Kapitel 1: Grundlagen Fibonacci-Zahlen Fibonacci-Zahlen Wenn Wenn fnfn die dieAnzahl Anzahlder derKaninchen Kaninchenzu zuBeginn Beginndes desn-ten n-tenMonats Monats bezeichnet. Dann sind die f genau die Fibonacci-Zahlen: bezeichnet. Dann sind die nf genau die Fibonacci-Zahlen: n 1, 1,1, 1,2, 2,3, 3,5, 5,8, 8,13, 13,21, 21,34, 34,55, 55,89, 89,... ... Definition Definitionder derFibonacci-Zahlen: Fibonacci-Zahlen: und und ffn ==ffn–1++ffn–2 n n–1 n–2 ff1 ==1, 1, ff22==1. 1. 1 Kurz: Jedes Folgenglied ist die Summe Kurz: Jedes Folgenglied ist die Summeseiner seinerbeiden beidenVorgänger. Vorgänger. © Dr. Zschiegner 2008 Seite 106 Kapitel 1: Grundlagen Seite Kaninchenvermehrung Kaninchenvermehrung © Dr. Zschiegner 2008 Seite 107 Kapitel 1: Grundlagen Beispiele Beispieleaus ausder derBiologie Biologie •• Bei BeiPflanzen Pflanzenkommen kommen Fibonacci-Zahlen Fibonacci-Zahlenhäufig häufigvor. vor. •• Bei BeiSonnenblumen Sonnenblumensind sinddie dieKerne Kerne ininSpiralen Spiralenangeordnet, angeordnet,die dienach nach links linksund undnach nachrechts rechtsdrehen. drehen.Die Die Anzahlen der linksdrehenden und Anzahlen der linksdrehenden und der derrechtsdrehenden rechtsdrehendenSpiralen Spiralen sind sindaufeinanderfolgende aufeinanderfolgende Fibonacci-Zahlen. Fibonacci-Zahlen. Ähnlich Ähnlichbei beiTannenzapfen, Tannenzapfen, Gänseblümchen, Gänseblümchen,Ananas, Ananas,… … © Dr. Zschiegner 2008 Seite 108 Kapitel 1: Grundlagen Seite Wie Wiekann kannman manFibonacci-Zahlen Fibonacci-Zahlenausrechnen? ausrechnen? 1. 1.Durch DurchAnwenden Anwendender derrekursiven rekursivenDefinition. Definition. 2. 2.Durch DurchAnwenden Anwendender derfolgenden folgendenexpliziten explizitenFormel: Formel: 1.4.3.1 1.4.3.1Satz Satz(Binet-Formel). (Binet-Formel).Für Fürjede jedenatürliche natürlicheZahl Zahl nn≥≥11 gilt gilt n n fnf ==[((1+√5)/2) [((1+√5)/2)n––((1–√5)/2) ((1–√5)/2)n]]//√5. √5. n Bemerkung. Bemerkung.Das DasErstaunliche Erstaunlichean andieser dieserFormel Formelist, ist,dass dasssich sichfür für jedes jedes nn die dieWurzelterme Wurzeltermeso soweg wegheben, heben,dass dassnur nureine einenatürliche natürliche Zahl, Zahl,nämlich nämlich fnfn stehenbleibt. stehenbleibt. © Dr. Zschiegner 2008 Seite 109 Kapitel 1: Grundlagen Beweis Beweis(Induktionsbasis) (Induktionsbasis) Beweis Beweisdurch durchInduktion Induktionnach nach n. n.Die DieAussage Aussage A(n) A(n) ist ist A(n): A(n): n n fnf ==[((1+√5)/2) [((1+√5)/2)n––((1–√5)/2) ((1–√5)/2)n]]//√5. √5. n Induktionsbasis: Induktionsbasis:Sei Sei nn==1. 1.Wir Wirmüssen müssendie dieAussage AussageA(1) A(1)beweisen. beweisen. Dazu Dazu rechnen rechnen wir wir einfach einfach die die Formel Formel (also (also die die rechte rechte Seite) Seite) für für den den Fall Fall nn==11 aus: aus: 1 1 [((1+√5)/2) ((1–√5)/2)1]]//√5 √5==[(1+√5)/2 [(1+√5)/2––(1–√5)/2] (1–√5)/2]//√5 √5== [((1+√5)/2)1––((1–√5)/2) [2√5)/2] [2√5)/2]//√5 √5==11 Damit Damitgilt gilt A(1). A(1). Beweisen BeweisenSie SieA(2): A(2):Übungsaufgabe. Übungsaufgabe. © Dr. Zschiegner 2008 Seite 110 Kapitel 1: Grundlagen Seite Beweis Beweis(Induktionsschritt) (Induktionsschritt) Induktionsschritt: Induktionsschritt:Sei Sei nn eine einenatürliche natürlicheZahl Zahlmit mit nn≥≥2, 2,und undes es mögen die Aussagen A(n) und A(n–1) gelten. mögen die Aussagen A(n) und A(n–1) gelten. Wir Wirmüssen müssenzeigen, zeigen,dass dassdann dannauch auch A(n+1) A(n+1) gilt. gilt.Dazu Dazuverwenden verwenden wir die Rekursionsformel f = f + f , und wenden sowohl wir die Rekursionsformel n+1 f = nf + n–1 f , und wenden sowohlauf auf fnf n+1 n n–1 n also alsoauch auchauf auf fn–1 fn–1 die dieInduktionsvoraussetzung Induktionsvoraussetzungan: an: fn+1 f == f ==fnf ++fn–1 n+1 n n–1 n n n–1 n–1 [((1+√5)/2) ((1–√5)/2)n]]//√5 √5++[((1+√5)/2) [((1+√5)/2)n–1––((1–√5)/2) ((1–√5)/2)n–1]]//√5 √5 [((1+√5)/2)n––((1–√5)/2) n–1 n–1 ==[((1+√5)/2) [((1+√5)/2)n–1[(1+ [(1+√5)/2 √5)/2++1] 1]––((1–√5)/2) ((1–√5)/2)n–1[(1– [(1–√5)/2 √5)/2++1]] 1]]//√5 √5... ... Wie Wiekann kannman mandiese diesemonströse monströseFormel Formelauflösen auflösen??? ??? © Dr. Zschiegner 2008 Seite 111 Kapitel 1: Grundlagen Beweis Beweis(das (dasWunder) Wunder) Wir Wirkönnen könnendie diekleinen kleineneckigen eckigenKlammern Klammerngünstig günstigumformen: umformen: 2 2 [(1+√5)/2 [(1–√5)/2++1] 1]==[(1–√5)/2] [(1–√5)/2]2.. [(1+√5)/2++1] 1]==[(1+√5)/2] [(1+√5)/2]2==[(1–√5)/2 Man Mansieht siehtbeide beideFormeln Formelnsofort sofortein, ein,wenn wennman mandie diejeweiligen jeweiligenrechten rechten Seiten ausrechnet. Seiten ausrechnet. Nun Nunkann kannuns unsaber abernichts nichtsmehr mehrhindern, hindern,weiterzurechnen: weiterzurechnen: n–1 2 n–1 2 ... ...==[((1+√5)/2) [((1+√5)/2)n–1[(1+√5)/2] [(1+√5)/2]2––((1–√5)/2) ((1–√5)/2)n–1[(1–√5)/2] [(1–√5)/2]2]]//√5 √5 n+1 n+1 ==[((1+√5)/2) [((1+√5)/2)n+1––((1–√5)/2) ((1–√5)/2)n+1]]//√5. √5. ... ...und unddamit damitist istdie dieAussage Aussage A(n+1) A(n+1) bewiesen. bewiesen. Nach Nachdem demPrinzip Prinzipder dervollständigen vollständigenInduktion Induktiongilt giltalso alsodie dieAussage. Aussage. © Dr. Zschiegner 2008 Seite 112 Kapitel 1: Grundlagen Seite Simpson-Identität Simpson-Identität 1.4.3.2 1.4.3.2Satz. Satz.Für Fürjede jedenatürliche natürlicheZahl Zahl nn≥≥22 gilt gilt 2 n fn+1 (–1)n.. f ⋅f⋅fn–1 ––fnf 2==(–1) n+1 n–1 n und ff 22 unterscheiden sich nur um 1, mal um +1, In InWorten: Worten:fn+1 fn+1⋅f⋅fn–1 n–1 und n n unterscheiden sich nur um 1, mal um +1, mal malum um–1. –1. Beweis Beweisdurch durchInduktion Induktionnach nach n. n. Die DieAussage Aussage A(n) A(n) sei seidie dieAussage Aussagedes desSatzes. Satzes. Induktionsbasis. Induktionsbasis.Sei Sei nn==2. 2.Wir Wirmüssen müssendie dieAussage Aussage A(2) A(2) zeigen. zeigen. Dazu Dazurechnen rechnenwir wireinfach einfachdie dielinke linkeSeite Seiteaus: aus: 2 2 2 L.S. L.S.==f3f3⋅f⋅f11––f2f22==2⋅1 2⋅1––112==11==(–1) (–1)2==R.S. R.S. © Dr. Zschiegner 2008 Seite 113 Kapitel 1: Grundlagen Beweis Beweis(Induktionsschritt) (Induktionsschritt) Induktionsschritt. Induktionsschritt.Sei Sei nn eine einenatürliche natürlicheZahl Zahl ≥≥2, 2,und undes esgelte geltedie die Aussage A(n). Wir müssen A(n+1) zeigen. Auch dazu rechnen Aussage A(n). Wir müssen A(n+1) zeigen. Auch dazu rechnenwir wir einfach einfachdie dieentsprechende entsprechendelinke linkeSeite Seiteaus: aus: 2 2 fn+2 f 2==(f(fn+1 ++fnf ))⋅f⋅fn ––fn+1 f 2 f ⋅f⋅fn ––fn+1 n+2 n n+1 n+1 n n n+1 2 ==fn+1 fn+1⋅(f ⋅(fnn--fn+1 fn+1))++fnfn2 ==fn+1 – (–1)nn fn+1⋅(f ⋅(fnn--fn+1 fn+1))++fn+1 fn+1⋅f⋅fn–1 n–1 – (–1) (nach (nachInduktion) Induktion) n+1 ==fn+1 fn+1⋅(f ⋅(fnn--fn+1 fn+1++fn-1 fn-1))++(–1) (–1)n+1 n+1 n+1 ==fn+1 fn+1⋅0 ⋅0++(–1) (–1)n+1== (–1) (–1)n+1.. Somit Somitgilt giltdie dieAussage Aussage A(n+1). A(n+1). © Dr. Zschiegner 2008 Seite 114 Kapitel 1: Grundlagen Seite Aufgaben Aufgaben Zeigen ZeigenSie Siedurch durchInduktion Induktionnach nach n, n,dass dassfür fürdie dieFibonacci-Zahlen Fibonacci-Zahlen fnfn folgendes gilt: folgendes gilt: (a) (a)11++f2f2++f4f4++f6f6++... ...++f2n f2n==f2n+1 f2n+1.. (b) (b)fn+2 fn+2==fnfn++fn–1 fn–1++......++f1f1++1. 1. Kapitel 1: Grundlagen © Dr. Zschiegner 2008 Seite 115 Kapitel 1: Grundlagen © Dr. Zschiegner 2008 Seite 116 Seite 1.5 1.5 Kombinatorik Kombinatorik •• Binomialzahlen Binomialzahlen •• Permutationen Permutationen © Dr. Zschiegner 2008 Seite 117 Kapitel 1: Grundlagen Potenzmenge Potenzmenge Zur ZurErinnerung: Erinnerung:Eine EineMenge Menge M' M' ist isteine eineTeilmenge Teilmengeeiner einerMenge MengeM, M, falls jedes Element von M' auch ein Element von M ist. Wir falls jedes Element von M' auch ein Element von M ist. Wir schreiben: schreiben: M' M'⊆⊆M. M. „Triviale“ „Triviale“Teilmengen: Teilmengen:Jede JedeMenge Mengehat hatsich sichselbst selbstund unddie dieleere leereMenge Menge {{}}(auch ∅), die kein Element enthält, als Teilmenge. (auch ∅), die kein Element enthält, als Teilmenge. Die DieMenge Mengealler allerTeilmengen Teilmengenvon von M M heißt heißtPotenzmenge PotenzmengeP(M) P(M)von vonM. M. Beispiel: Beispiel: Alle AlleTeilmengen Teilmengenvon von M M=={a, {a,b, b,c} c} sind sind {{},},{a}, {a},{b}, {b},{c}, {c},{a, {a,b}, b},{a, {a,c}, c},{b, {b,c}, c},{a, {a,b, b,c}. c}. n 1.5.1 1.5.1Satz. Satz.Jede Jeden-elementige n-elementigeMenge MengeM Mhat hatgenau genau 22n Teilmengen. Teilmengen. © Dr. Zschiegner 2008 Seite 118 Kapitel 1: Grundlagen Seite Beweis Beweis Beweis Beweisdurch durchInduktion Induktionnach nach n. n. Induktionsbasis: Für n = 1 (n = 2, Induktionsbasis: Für n = 1 (n = 2,nn==3) 3)ist istdie dieBehauptung Behauptungrichtig. richtig. Induktionsschritt: Induktionsschritt:Sei Seinn>>1, 1,und undsei seidie dieBehauptung Behauptungrichtig richtigfür für n–1. n–1. Sei M eine n-elementige Menge, und sei m ein beliebiges Element Sei M eine n-elementige Menge, und sei m ein beliebiges Element aus aus M. M.Es Esgibt gibtzwei zweiSorten Sortenvon vonTeilmengen Teilmengenvon vonM: M:Solche, Solche,die die m m enthalten, enthalten,und undsolche, solche,die die m m nicht nichtenthalten. enthalten. Die DieTeilmengen Teilmengenvon von M, M,die die m m nicht nichtenthalten, enthalten,sind sindgenau genaudie dieTeilTeiln–1 mengen von M\{m}; davon gibt es nach Induktion genau 2 n–1 viele. mengen von M\{m}; davon gibt es nach Induktion genau 2 viele. Für Fürjede jedeTeilmenge Teilmenge M‘, M‘,die die m m enthält, enthält,ist ist M‘\{m} M‘\{m} eine eineTeilmenge Teilmenge n–1 von M\{m} und umgekehrt. Also gibt es auch hiervon 2 von M\{m} und umgekehrt. Also gibt es auch hiervon 2n–1 Stück. Stück. n–1 n–1 n–1 n Insgesamt Insgesamtgibt gibtes esalso also 22n–1++22n–1==2·2 2·2n–1==22nTeilmengen Teilmengenvon von M. M. © Dr. Zschiegner 2008 Seite 119 Kapitel 1: Grundlagen Binomialzahlen Binomialzahlen Definition. Teilmengen Definition.Die DieAnzahl Anzahlder derk-elementigen k-elementigen Teilmengeneiner einernnn elementigen Menge wird mit bezeichnet („n über k“); diese elementigen Menge wird mit k bezeichnet („n über k“); dieseZahlen Zahlen heißen Binomialzahlen. heißen Binomialzahlen. Beispiele Beispiele n ==11(jede (jedeMenge Mengehat hatgenau genaueine eine0-elem. 0-elem.Teilmenge, Teilmenge,nämlich nämlich {}) {}) 0 n = 1 (jede n-elementige Menge hat nur eine n-elementige Teil = 1 (jede n-elementige Menge hat nur eine n-elementige Teil n menge, nämlich sich selbst) menge, nämlich sich selbst) n ==nn(die (dieTeilmeng. Teilmeng.der derMächtigkeit Mächtigkeit11sind sindgenau genaudie diennElemente) Elemente) 1 4 ==66(die (die4-elementige 4-elementigeMenge Menge {a, {a,b, b,c,c,d} d} hat hatsechs sechs2-elementige 2-elementige 2 Teilmengen: Teilmengen:{a, {a,b}, b},{a, {a,c}, c},{a, {a,d}, d},{b, {b,c}, c},{b, {b,d}, d},{c, {c,d}) d}) © Dr. Zschiegner 2008 Seite 120 Kapitel 1: Grundlagen Seite Rekursionsformel Rekursionsformel für fürBinomialzahlen Binomialzahlen Wie Wiekann kannman mandie dieBinomialzahlen Binomialzahlenausrechnen? ausrechnen?1. 1.Methode: Methode: 1.5.2 1.5.2Rekursionsformel Rekursionsformelfür fürBinomialzahlen. Binomialzahlen.Seien Seien kk und und nn natürliche natürlicheZahlen Zahlenmit mit 11≤≤kk≤≤n. n.Dann Danngilt gilt n n − 1 n − 1 = + . k k k − 1 Beispiel: Beispiel: 6 5 5 4 4 5 = + = + + =6 + 4 + 5=15. 2 2 1 2 1 1 © Dr. Zschiegner 2008 Seite 121 Kapitel 1: Grundlagen Beweis Beweis der der Rekursionsformel Rekursionsformel Sei Sei M Meine eineMenge Mengemit mit nn Elementen. Elementen.Sei Seim mein einElement Elementvon vonM. M. Wir teilen die k-elementigen Teilmengen von M in zwei Klassen Wir teilen die k-elementigen Teilmengen von M in zwei Klassenein: ein: 1. Klasse: die, die m nicht enthalten. Jede dieser Teilmengen ist eine 1. Klasse: die, die m nicht enthalten. Jede dieser Teilmengen ist einekkelementige elementigeTeilmenge Teilmengeder der(n–1)-elementigen (n–1)-elementigenMenge Menge M M\\{m}. {m}.Also Alsogibt gibt n − 1 es esdavon davongenau genau k Stück. Stück. 2. 2.Klasse: Klasse:die diek-elementige k-elementigeTeilmengen, Teilmengen,die diem menthalten. enthalten.Sei Sei M’ M’ eine eine Teil-menge aus dieser Klasse. Wir entfernen m aus M’ und aus Teil-menge aus dieser Klasse. Wir entfernen m aus M’ und aus M. M. Dann Dannist ist M’ M’\\{m} {m} eine eine(k–1)-elem. (k–1)-elem.Teilmenge Teilmengeder der(n–1)-elem. (n–1)-elem.Menge Menge M\{m}. M\{m}.Umgekehrt Umgekehrtkann kannman manjede jede(k–1)-elem. (k–1)-elem.Teilmenge Teilmengevon von M M\\{m} {m} durch durchHinzufügen Hinzufügenvon von m m zu zueiner einerTeilmenge Teilmengeder derKlasse Klasse22ergänzen. ergänzen. n − 1 Somit Somitist istdie dieAnzahl Anzahlder derTeilmengen Teilmengenininder derKlasse Klasse22gleich gleich k − 1 .. Durch DurchAddition Additionder derbeiden beidenAnzahlen Anzahlenergibt ergibtsich sichdie dieFormel. Formel. © Dr. Zschiegner 2008 Seite 122 Kapitel 1: Grundlagen Seite Explizite ExpliziteFormel Formelfür fürBinomialzahlen Binomialzahlen Zweite ZweiteBerechnungsmethode Berechnungsmethodefür fürBinomialzahlen: Binomialzahlen: 1.5.3 1.5.3Explizite ExpliziteFormel Formelfür fürdie dieBinomialzahlen. Binomialzahlen.Seien Seien kk und und nn natürliche natürlicheZahlen Zahlenmit mit 00≤≤kk≤≤n. n.Dann Danngilt gilt n n! n ⋅ (n − 1) ⋅ (n − 2) ⋅ ... ⋅ (n − k + 1) = = . k! k k!⋅(n − k )! n! n!(„n („nFakultät”) Fakultät”)ist istdefiniert definiertals als n! n!==nn⋅ ⋅(n (n––1) 1)⋅ ⋅(n (n––2) 2)⋅ ⋅... ...⋅ ⋅22⋅ ⋅1. 1. Beispiel: Beispiel: 5! 5!==55⋅ ⋅44⋅ ⋅33⋅ ⋅22⋅ ⋅11==120. 120. n n(n − 1) Beispiel Beispielzur zurexpliziten explizitenFormel: Formel: 2 = 2 . © Dr. Zschiegner 2008 Seite 123 Kapitel 1: Grundlagen Beweis Beweis der der expliziten expliziten Formel Formel Der DerBeweis Beweiserfolgt erfolgtdurch durchInduktion Induktionnach nach n. n.Wir Wirmachen machenuns unshier hierden den Schritt von 5 auf 6 klar. Wir setzen also voraus, dass die Formel Schritt von 5 auf 6 klar. Wir setzen also voraus, dass die Formel schon schonfür für nn==55 richtig richtigist. ist.Dann Dannschließen schließenwir wirwie wiefolgt folgtweiter weiter 6 5 5 5! 5! = + = + k k k − 1 k ! ( 5 − k )! ( k − 1 )! ⋅ ( 5 − k + 1)! = 5! 1 1 5! (5 − k + 1) + k ⋅ ( + )= (k − 1)!⋅(5 − k )! k 5 − k + 1 (k − 1)!⋅(5 − k )! k(5 − k + 1) = 6 ⋅ 5! 6! = . k ⋅ (k − 1)!⋅(6 − k ) ⋅ (5 − k )! k!⋅(6 − k )! © Dr. Zschiegner 2008 Seite 124 Kapitel 1: Grundlagen Seite Möglichkeiten Möglichkeitenbeim beimLotto Lotto Beispiel. Beispiel.Beim BeimLotto Lotto“6 “6aus aus49” 49”werden werdensechs sechsder derZahlen Zahlen1, 1,2, 2,..., ...,49 49 gezogen, gezogen,wobei wobeies esauf aufdie dieReihenfolge Reihenfolgenicht nichtankommt. ankommt. In Inunserer unsererSprache Spracheheißt heißtdas: das:Es Eswird wirdeine eine6-elementige 6-elementigeTeilmenge Teilmenge der Menge {1, 2, ..., 49} gezogen. der Menge {1, 2, ..., 49} gezogen. 49 Dafür Dafürgibt gibtes esnach nachDefinition Definitiongenau genau Möglichkeiten. Möglichkeiten. 6 49 49! 49 ⋅ 48 ⋅ 47 ⋅ 46 ⋅ 45 ⋅ 44 = = 6! 6 6!⋅(43)! ==13.983.816. 13.983.816. Die DieWahrscheinlichkeit Wahrscheinlichkeitfür für66Richtige Richtigeist istalso also1/13.983.816 1/13.983.816== 0,000000071… 0,000000071… © Dr. Zschiegner 2008 Seite 125 Kapitel 1: Grundlagen Aufgaben Aufgaben 42 47 1. 1.Berechnen BerechnenSie Sie 11 und und 40 .. 2. 2.Auf Aufeiner einerParty Partysind sind 10 10 Gäste. Gäste.Zu ZuBeginn Beginnstößt stößtjeder jedermit mitjedem jedem anderen Gast genau einmal an. anderen Gast genau einmal an. (a) (a)Wie Wieoft oftklingen klingenzwei zweiGläser Gläserzusammen? zusammen? (b) (b) Auf Aufeiner eineranderen anderenParty Partystößt stößtebenfalls ebenfallsjeder jedermit mitjedem jedemanderen anderen an. Man hört 55 mal Gläser klingen. Wie viele Teilnehmer waren an. Man hört 55 mal Gläser klingen. Wie viele Teilnehmer warenda? da? (c) (c)Bei Beieiner einerdritten drittenParty Partybehauptet behauptetjemand, jemand,dass dasses esgenau genau 50 50 mal mal geklungen hat. Was sagen Sie dazu? geklungen hat. Was sagen Sie dazu? © Dr. Zschiegner 2008 Seite 126 Kapitel 1: Grundlagen Seite Aufgaben Aufgaben 1. 1.Auf Aufden denüblichen üblichenDominosteinen Dominosteinensind sinddie diesieben siebenZahlen Zahlen 0, 0,1,..., 1,...,66 aufgemalt. aufgemalt.Dabei Dabeikommen kommenalle allemöglichen möglichenKombinationen Kombinationenaus auszwei zwei Zahlen vor. Aus wie vielen Dominosteinen besteht ein vollständiges Zahlen vor. Aus wie vielen Dominosteinen besteht ein vollständiges Spiel? Spiel? 2. 2.Schlüssel Schlüsselwerden werdengemacht, gemacht,indem indemman manSchlitze Schlitzeverschiedener verschiedenerTiefe Tiefe ininden denBart Barteinfräst. einfräst.Angenommen, Angenommen,es esgibt gibt88verschiedene verschiedeneTiefen. Tiefen.Wie Wie viel Schlitze muss man vorsehen, um 1 Million verschiedener Schlüssel viel Schlitze muss man vorsehen, um 1 Million verschiedener Schlüssel machen machenzu zukönnen? können? n n 3. 3.Zeigen ZeigenSie Sie k = n − k ,,indem indemSie Siemit mitTeilmengen Teilmengeneiner einerMenge Menge argumentieren. argumentieren. © Dr. Zschiegner 2008 Seite 127 Kapitel 1: Grundlagen Aufgabe Aufgabe Machen MachenSie Siesich sichklar, klar,wie wieman manmit mitHilfe Hilfedes desPascalschen PascalschenDreiecks Dreiecksdie die Binomialzahlen bestimmen kann. Welche Formel steckt dahinter? Binomialzahlen bestimmen kann. Welche Formel steckt dahinter? Was Wasergibt ergibtsich sichfür fürdie dieZeilensummen Zeilensummenim imPascalschen PascalschenDreieck Dreieck––und und warum? warum? © Dr. Zschiegner 2008 Seite 128 Kapitel 1: Grundlagen Seite Binomischer BinomischerLehrsatz Lehrsatz 2 2 2 Erinnerung: Erinnerung:(a (a±±b) b)2==aa2±±2ab 2ab+b +b2(1./2. (1./2.binomische binomischeFormel). Formel). 1.5.4 1.5.4Binomialsatz. Binomialsatz.Seien Seien xx und und yy Unbestimmte Unbestimmteüber überR. R.Dann Danngilt gilt für fürjede jedenatürliche natürlicheZahl Zahl nn die diefolgende folgendeGleichung: Gleichung: n n–2 2 n 2 n–2 n n n–1 n–1 n (x+y) (x+y)n==xxn++nx nxn–1yy++ 2 xxn–2yy2++... ...++ 2 xx2yyn–2++nxy nxyn–1++yyn.. 3 Zum ZumBeispiel Beispielgilt gilt (Ping (Ping++Pong) Pong)3 3 2 2 3 ==Ping Ping3++3Ping 3Ping2Pong Pong++3PingPong 3PingPong2++Pong Pong3.. 3 3 Beispiele. Beispiele.31 313==(30 (30++1) 1)3 3 2 2 3 ==30 303++3⋅30 3⋅302⋅1 ⋅1++3⋅30⋅1 3⋅30⋅12 ++113==27.000 27.000++2.700 2.700++90 90++11==29.791. 29.791. 5 5 4 3 2 2 3 4 5 (s–3t) (s–3t)5==ss5--5s 5s4(3t) (3t)++10s 10s3(3t) (3t)2--10s 10s2(3t) (3t)3++5s(3t) 5s(3t)4--(3t) (3t)5==... ... © Dr. Zschiegner 2008 Seite 129 Kapitel 1: Grundlagen Beweis Beweisdes desBinomialsatzes Binomialsatzes Beweis. Beweis.Wir Wirstellen stellenuns unsvor, vor,wie wieman mandie dielinke linkeSeite Seiteausrechnet: ausrechnet: Man müsste n mal die Terme x+y miteinander multiplizieren. Man müsste n mal die Terme x+y miteinander multiplizieren. Wenn Wennman mandies diesausmultiplizieren ausmultiplizierenwürde, würde, würde man aus k dieser Terme x würde man aus k dieser Terme x und undaus ausden denandern andern n–k n–k die dieVariable Variable yy auswählen. auswählen. k n–k Also Alsoerhält erhältman manAusdrücke Ausdrückeder derForm Form xxkyyn–k.. k n–k Die DieFrage Frageist, ist,wie wieoft oftman mandabei dabeiden denSummand Summand xxkyyn–k erhält. erhält. Um diesen Term zu erhalten, muss man x genau k mal Um diesen Term zu erhalten, muss man x genau k malunter unter nn Möglichkeiten Möglichkeitenauswählen. auswählen. n k n–k Daher erhält man Daher erhält manden denSummand Summand xxkyyn–k genau genau k mal. mal. © Dr. Zschiegner 2008 Seite 130 Kapitel 1: Grundlagen Seite Anwendungen Anwendungendes desBinomialsatzes Binomialsatzes Man Mankann kannden denBinomialsatz Binomialsatzauch auchfür fürfeste festeWerte Wertevon von xx und und yy spezialisieren spezialisierenund und nn allgemein allgemeinlassen. lassen.Man Manerhält erhälteine eineAussage Aussage über Binomialzahlen, die man dann in eine Aussage über über Binomialzahlen, die man dann in eine Aussage über Teilmengen Teilmengenübersetzen übersetzenkann. kann.Zwei ZweiBeispiele. Beispiele. 1.5.5 1.5.5Anzahl Anzahlaller allerTeilmengen. Teilmengen.Wir Wirsetzen setzen xx==yy==1. 1.Wir Wirerhalten: erhalten: n n n n n n n ++ ++ ++... ...++ n −1++ n ==(1+1) (1+1)n==22n.. 0 1 2 Dies Diessagt, sagt,dass dassdie dieAnzahl Anzahlaller allerTeilmengen Teilmengeneiner einern-elementigen n-elementigen Menge (das heißt die Anzahl der 0-elementigen Teilmengen Menge (das heißt die Anzahl der 0-elementigen Teilmengenplus plusdie die n Anzahl der 1-elementigen Teilmengen plus ...) gleich 2 n ist. Anzahl der 1-elementigen Teilmengen plus ...) gleich 2 ist. © Dr. Zschiegner 2008 Seite 131 Kapitel 1: Grundlagen Gerade Geradeund undungerade ungeradeTeilmengen Teilmengen 1.5.6 1.5.6Satz. Satz.Anzahl Anzahlder dergeraden geradenTeilmengen Teilmengen==Anzahl Anzahlder derungeraden ungeraden Teilmengen. Teilmengen. Beweis. Beweis.Wir Wirsetzen setzenxx==1, 1,yy==–1 –1und underhalten erhalten n n n n n n n –– ++ –– ++ –/+ –/+... ...==(1 (1––1) 1)n==00n==0. 0. 0 1 2 3 4 M.a.W.: M.a.W.:Die Diealternierende alternierendeSumme Summeder derBinomialzahlen Binomialzahlenist istNull. Null. Wir interpretieren dies auf folgende Weise: Die Anzahl der Wir interpretieren dies auf folgende Weise: Die Anzahl der Teilmengen Teilmengenmit mitgerader geraderMächtigkeit Mächtigkeitist istgleich gleichder derAnzahl Anzahlder der Teilmengen ungerader Mächtigkeit. Teilmengen ungerader Mächtigkeit. © Dr. Zschiegner 2008 Seite 132 Kapitel 1: Grundlagen Seite Aufgabe Aufgabe 4 1. 1.Multiplizieren MultiplizierenSie Sie(a (a++b) b)4mit mitHilfe Hilfedes desPascalschen PascalschenDreiecks Dreiecksaus. aus. 3 2. 2.Berechnen BerechnenSie Sie41 413.. © Dr. Zschiegner 2008 Seite 133 Kapitel 1: Grundlagen Permutationen Permutationen Definition. Definition.Eine EinePermutation Permutationeiner einerendlichen endlichenMenge Menge M M ist isteine eine bijektive Abbildung der Menge M in sich. D.h.: Jedem Element bijektive Abbildung der Menge M in sich. D.h.: Jedem Elementaus aus M M wird wirdein einElement Elementvon von M M so sozugeordnet, zugeordnet,dass dasskeine keinezwei zwei Elemente Elementedas dasgleiche gleicheBild Bildhaben. haben. Beispiel: Beispiel:Die DieAbbildung Abbildung ππ definiert definiertdurch durch π(1) π(1)==2, 2,π(2) π(2)==4, 4,π(3) π(3)== 3, 3,π(4) π(4)==5, 5,π(5) π(5)==11 ist isteine einePermutation Permutationder derMenge Menge {1, {1,2, 2,3, 3,4, 4,5}. 5}. © Dr. Zschiegner 2008 Seite 134 Kapitel 1: Grundlagen Seite Anzahl Anzahlder derPermutationen Permutationen 1.5.8 1.5.8 Satz. Satz. Die Die Anzahl Anzahl der der Permutationen Permutationen einer einer n-elementigen n-elementigen Menge ist n! Menge ist n! Beispiel: Beispiel:Um Um100 100Menschen Menschenauf auf100 100Stühle Stühlezu zusetzen, setzen, 158 gibt es genau 100! ≈ 10 158 Möglichkeiten. gibt es genau 100! ≈ 10 Möglichkeiten. Beweis. Beweis.Wir Wirüberlegen überlegenuns unssystematisch, systematisch,wie wieviele vieleMöglichkeiten Möglichkeitenes es für füreine einePermutation Permutation ππ einer einern-elementigen n-elementigenMenge Menge M M gibt. gibt. Ohne OhneEinschränkung Einschränkungkönnen könnenwir wir M M=={1, {1,2, 2,3, 3,..., ...,n} n} wählen. wählen. Wir überlegen uns der Reihe nach, wie viele Möglichkeiten Wir überlegen uns der Reihe nach, wie viele Möglichkeitenes esfür fürdie die Bilder Bilderder derElemente Elemente 1, 1,2, 2,3, 3,..., ...,nn gibt. gibt. © Dr. Zschiegner 2008 Seite 135 Kapitel 1: Grundlagen Beweis Beweis Für Fürdas dasBild Bilddes desersten erstenElements Elements 11 gibt gibtes es nn Möglichkeiten. Möglichkeiten. Für Fürdas dasBild Bildvon von 2: 2: n–1 n–1 Möglichkeiten, Möglichkeiten,nämlich nämlichalle alleaußer außerdem dem Bild π(1) des ersten Elements. Bild π(1) des ersten Elements. Für Fürdas dasBild Bildvon von 3: 3: n–2 n–2 Möglichkeiten Möglichkeiten(alle (alleaußer außer π(1) π(1) und und π(2)). π(2)). Usw. Usw. Bild Bildvon von n–1: n–1: 22 Möglichkeiten, Möglichkeiten,da dabereits bereits n–2 n–2 Elemente Elementevergeben vergeben sind (die Bilder von 1, 2, ..., n–2). sind (die Bilder von 1, 2, ..., n–2). Das DasBild Bilddes desletzten letztenElements Elementsist istvollständig vollständigdeterminiert. determiniert. Also Alsogibt gibtes esinsgesamt insgesamtgenau genau n⋅(n–1) n⋅(n–1)(n–2) (n–2)... ...2⋅1 2⋅1==n! n! MöglichMöglichkeiten für die Auswahl einer beliebigen Permutation π von keiten für die Auswahl einer beliebigen Permutation π von M. M. © Dr. Zschiegner 2008 Seite 136 Kapitel 1: Grundlagen Seite Aufgaben Aufgaben 1. 1.Wie Wieviele vieleMöglichkeiten Möglichkeitengibt gibtes, es,acht achtTürme Türmeso soauf aufeinem einem Schachbrett aufzustellen, dass keine zwei sich gegenseitig Schachbrett aufzustellen, dass keine zwei sich gegenseitigbedrohen? bedrohen? 2. 2.Wie Wieviele viele5-stellige 5-stelligePostleitzahlen Postleitzahlengibt gibtes? es? 3. 3.Ist Istes esbesser, besser,zwei zwei3-stellige 3-stelligeZahlenschlösser Zahlenschlösseroder oderein ein6-stelliges 6-stelligeszu zu benutzen? benutzen? 4. 4.Ein EinKollege Kollegeerzählt erzähltmir: mir:„Ich „Ichhabe habeeine einegute gutePIN: PIN:lauter lauterverschiedene verschiedene Ziffern!“ Wie viele Möglichkeiten für PINs aus verschiedenen Ziffern!“ Wie viele Möglichkeiten für PINs aus verschiedenenZiffern Ziffern gibt es? Wie viel hat mir mein Kollege also von seiner PIN verraten? gibt es? Wie viel hat mir mein Kollege also von seiner PIN verraten? Kapitel 1: Grundlagen © Dr. Zschiegner 2008 Seite 137 Kapitel 1: Grundlagen © Dr. Zschiegner 2008 Seite 138 Seite