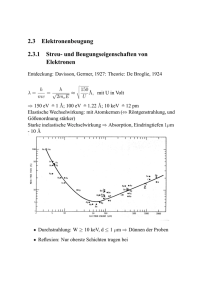
Übung 3 - IWR Heidelberg
Werbung

Mathematik für Naturwissenschaftler II SS 2017
Prof. Andreas Dreuw, Manuel Hodecker, Adrian Dempwolff
Ausgabe:
Abgabe:
Übungsblatt 3
1
2
3
4
Do 04.05.2017
Fr 12.05.2017 10:00
Σ
/ 24 P
Aufgabe 3.1 (8 P). Gegeben seien die drei Vektoren
1
0
1
~b = 1 1 ,
1 ,
~a =
1
−1
Na
Nb
1
0
−1
1
0
~c =
0
Nc
1
(a) Bestimmen Sie die Konstanten Na , Nb und Nc so, dass die Vektoren die Länge 1 haben.
(2 P)
(b) Zeigen Sie, dass die Vektoren orthogonal zueinander sind.
(2 P)
(c) Bestimmen Sie einen vierten Vektor d~ so, dass ~a, ~b, ~c und d~ eine Orthonormalbasis des
R4 bilden.
(4 P)
Aufgabe 3.2 (5 P). Seien V der reelle Vektorraum der stetigen Funktionen auf dem Intervall
[−1, 1] und f, g, h ∈ V . Zeigen Sie mit Hilfe der Eigenschaften der Integralrechnung, dass
Z1
hf |gi =
f (x)g(x) dx
−1
die Regeln für ein Skalarprodukt
(a) hf |gi = hg|f i
(1 P)
(b) αhf |gi = hαf |gi = hf |αgi für alle α ∈ R
(2 P)
(c) hf |g + hi = hf |gi + hf |hi
(2 P)
erfüllt.
Aufgabe 3.3 (3 P). Seien V und das Skalarprodukt gegeben wie in Aufgabe 3.2.
(a) Zeigen Sie, dass sin(x) senkrecht auf cos(x) steht.
(1 P)
(b) Bestimmen Sie α so, dass f (x) = 1 senkrecht auf g(x) = α + x steht.
(2 P)
Aufgabe 3.4 (8 P). Vergleichen Sie die Gaußsche Zahlenebene der komplexen Zahlen C
mit dem reellen Vektorraum R2 .
(a) Erklären Sie, warum die imaginäre Einheit ı und der Einheitsvektor ~eˆ2 , sowie die Zahl
1 und der Einheitsvektor ~eˆ1 einander äquivalent sind.
(2 P)
1
(b) Stellen Sie mittels der Basis {~eˆ1 , ~eˆ2 } aus (a) eine komplexe Zahl a + ıb ∈ C als Vektor
im R2 dar.
(1 P)
(c) Welcher komplexen Operation entspricht die Multiplikation der Matrix
1 0
0 −1
mit einem Vektor
x1
x2
?
(2 P)
(d) Gegeben seien zwei komplexe Zahlen z1 = a + ıb und z2 = c + ıd. Zeigen Sie, dass die
Matrix
c −d
d c
angewendet auf den zu z1 äquivalenten Vektor im R2 der Multiplikation der komplexen
Zahlen z1 und z2 entspricht.
(3 P)
Beachten Sie. Die Matrix-Vektor-Multiplikation im R2 ist gegeben durch
m11 m12
a
m11 a + m12 b
=
m21 m22
b
m21 a + m22 b
2