Mathplan 7.8.1 - educa.Unterricht

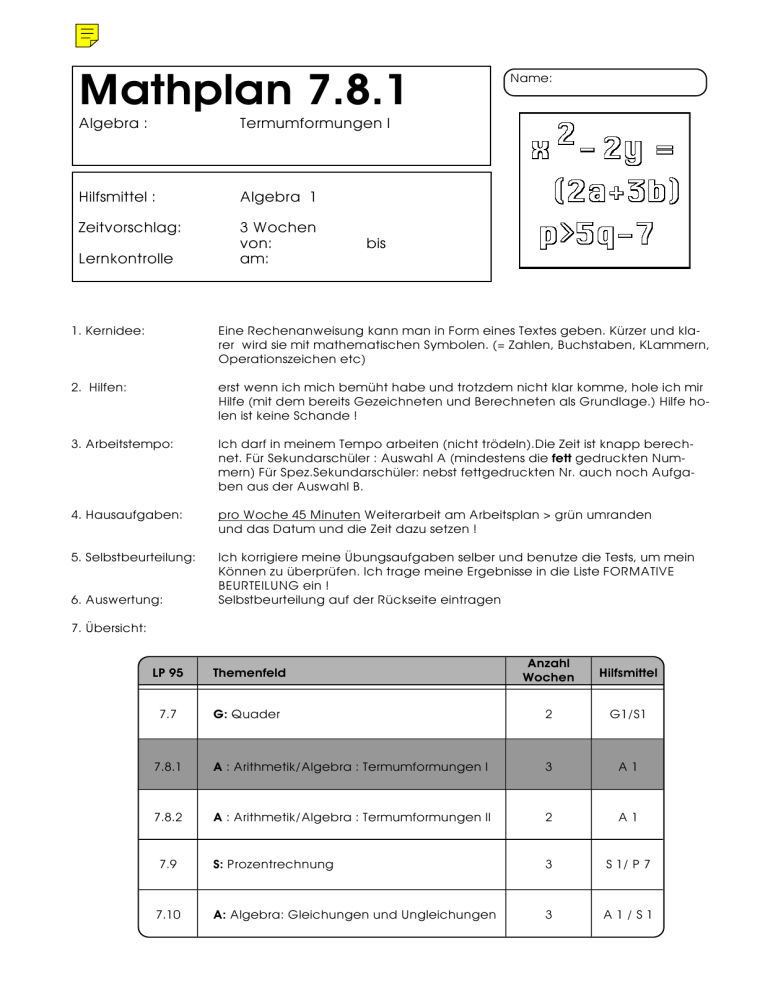
Mathplan 7.8.1
Algebra :
Termumformungen I
Hilfsmittel :
Algebra 1
Zeitvorschlag:
3 Wochen
von:
am:
Lernkontrolle
Name:
bis
1. Kernidee:
Eine Rechenanweisung kann man in Form eines Textes geben. Kürzer und klarer wird sie mit mathematischen Symbolen. (= Zahlen, Buchstaben, KLammern,
Operationszeichen etc)
2. Hilfen:
erst wenn ich mich bemüht habe und trotzdem nicht klar komme, hole ich mir
Hilfe (mit dem bereits Gezeichneten und Berechneten als Grundlage.) Hilfe holen ist keine Schande !
3. Arbeitstempo:
Ich darf in meinem Tempo arbeiten (nicht trödeln).Die Zeit ist knapp berechnet. Für Sekundarschüler : Auswahl A (mindestens die fett gedruckten Nummern) Für Spez.Sekundarschüler: nebst fettgedruckten Nr. auch noch Aufgaben aus der Auswahl B.
4. Hausaufgaben:
pro Woche 45 Minuten Weiterarbeit am Arbeitsplan > grün umranden
und das Datum und die Zeit dazu setzen !
5. Selbstbeurteilung:
Ich korrigiere meine Übungsaufgaben selber und benutze die Tests, um mein
Können zu überprüfen. Ich trage meine Ergebnisse in die Liste FORMATIVE
BEURTEILUNG ein !
Selbstbeurteilung auf der Rückseite eintragen
6. Auswertung:
7. Übersicht:
LP 95
Themenfeld
Anzahl
Wochen
Hilfsmittel
7.7
G: Quader
2
G1/S1
7.8.1
A : Arithmetik/Algebra : Termumformungen I
3
A1
7.8.2
A : Arithmetik/Algebra : Termumformungen II
2
A1
7.9
S: Prozentrechnung
3
S 1/ P 7
7.10
A: Algebra: Gleichungen und Ungleichungen
3
A1/S1
Inhalte, Begriffe, Hilfsmittel
Auswahl A
Auswahl B
Terme mit Zahlen und Variablen über Q + ° mit einer Var.
A1: 211, 212,
A1: 215
Terme und Formeln aus Sachzusammenhängen gewinnen
Terme auswerten
Zusammenfassung
A1: 221, 222, 223
A1: 224, 225
A1: 231, 233, 234, 237
A1: 232, 235, 236
213, 214
Test 7.8.1
Termumformungen
Vorbereitung mit Zahlentermen,
A1: 241
A1: 242, 243, 244
Vereinfachen von Summen und
Differenzen
A1: 311, 312, 313, 314, 315,
316, 317, 318
A1: 3101, 3102, 3103,
3104, 3105, 3106
Test 7.8.2
Operieren mit vereinfachten
Summen; Rechengesetze
A1: 321, 322, 323, 324, 325,
326, 327, 328
Test 7.8.3
A1: 3201, 3203, 3204,
3205
Test 7.8.4
Vereinfachen von Produkten
und Quotienten; Potenzen
(algebraisch); Rechengesetze
Operieren mit vereinfachten
Produkten; Potenzen
A1: 331, 332, 333, 334, 335,
336, 337, 338
A1: 3301, 3302, 3303
3304, 3305, 3306
A1: 341, 342, 343, 344, 345,
346, 347, 348, 349
A1: 3401, 3402, 3403,
3404, 3405 3406
Test 7.8.5
Zusammenfassung
Lernkontrolle 7.8.1
Testserie 3 LA S. 77
Selbstbeurteilung:
a) Arbeitsweise: schnell, flüchtig, langsam, gründlich,
sauber, unübersichtlich.
was trifft für mich zu? > Begründung
b) Was ich sonst noch sagen möchte:
Der Lehrer:
Die Eltern:
Test 7.8.6
.
Bearbeitet am:
ZAHLENMENGEN :
ZAHLENMENGEN :
Menge der natürlichen Zahlen
Zahlen,die man beim Zählen braucht.
{1,2,3,4...}
{0,1,2,3...}
N
Z
Menge der ganzen Zahlen
alle positiven und negativen ganzen Zahlen
{...-2,-1,0,1,2,3...}
Z
Menge der ganzen Zahlen
alle positiven und negativen ganzen Zahlen
{...-2,-1,0,1,2,3...}
Q
Menge der rationalen Zahlen
alle Zahlen, die sich als Bruch schreiben
lassen.
Q
Menge der rationalen Zahlen
alle Zahlen, die sich als Bruch schreiben
lassen.
N
No
z.B.
No
 1 3 2 4
− ,− , , 
 3 8 5 1
Menge der natürlichen Zahlen
Zahlen,die man beim Zählen braucht.
{1,2,3,4...}
{0,1,2,3...}
z.B.
 1 3 2 4
− ,− , , 
 3 8 5 1
Qo
Qo+
Menge der rationalen Zahlen und 0
Menge der irrationalen Zahlen:
die Zahlen sind nicht mehr als gemeiner Bruch darstellbar
es sind nichtperiodische Dezimalbrüche zB: π , √2etc
I
Menge der irrationalen Zahlen:
die Zahlen sind nicht mehr als gemeiner Bruch darstellbar
es sind nichtperiodische Dezimalbrüche zB: π , √2etc
Menge der reellen Zahlen : enthält alle rationalen und alle
irrationalen Zahlen.
R
Menge der reellen Zahlen : enthält alle rationalen und alle
irrationalen Zahlen.
Qo
Qo+
Menge der rationalen Zahlen und 0
I
R
Menge aller positiven rationalen Zahlen und 0
Menge aller positiven rationalen Zahlen und 0
SYMBOLE :
SYMBOLE :
=
=
≥
≠
∈
∉
≈
∞
gleichgross
kleiner oder gleichgross (höchstens)
grösser oder gleichgross (mindestens)
ist nicht gleichgross
ist ein Element von
ist kein Element von
gerundet, äequivalent zu
unendlich
≥
≠
∈
∉
≈
∞
gleichgross
kleiner oder gleichgross (höchstens)
grösser oder gleichgross (mindestens)
ist nicht gleichgross
ist ein Element von
ist kein Element von
gerundet, äequivalent zu
unendlich
ALGEBRA 1
ALGEBRA 1
Algebraische Abmachungen
Algebraische Abmachungen
Variable : a , x etc.
als Variable bezeichnet man einen Buchstaben
(oder ein anderes Zeichen), an dessen Stelle eine beliebige Zahl aus einer gegebenen Menge
gesetzt werden kann.
Variable : a , x etc.
als Variable bezeichnet man einen Buchstaben
(oder ein anderes Zeichen), an dessen Stelle eine beliebige Zahl aus einer gegebenen Menge
gesetzt werden kann.
Term:
Als Term bezeichnet man allgemein:
- einzelne Zahlen
- einzelne Variablen und
- sinnvolle Zusammenstellungen von Zahlen,
Variablen, Operationszeichen und Klammern
Term:
Als Term bezeichnet man allgemein:
- einzelne Zahlen
- einzelne Variablen und
- sinnvolle Zusammenstellungen von Zahlen,
Variablen, Operationszeichen und Klammern
25
bc
3(x+5) = a
25
bc
3(x+5) = a
0+a = a+0 = a
0 ist das neutrale Element der Addition und
Subtraktion.
0+a = a+0 = a
0 ist das neutrale Element der Addition und
Subtraktion.
1·a = a·1 = a
1 ist das neutrale Element der Multiplikation
und Division.
1·a = a·1 = a
1 ist das neutrale Element der Multiplikation
und Division.
3 · s = 3s
a · b = ab
4 · (a+b) = 4(a+b)
a · (x-y) = a(x-y)
aber
4·3
43
Zwischen Zahlen, Buchstaben und Klammern
kann das · Zeichen weggelassen werden.
Zwischen 2 Zahlen die durch eine Multiplikation
verknüpft sind muss immer ein · Zeichen gesetzt werden.
3 · s = 3s
a · b = ab
4 · (a+b) = 4(a+b)
a · (x-y) = a(x-y)
aber
4·3
43
Zwischen Zahlen, Buchstaben und Klammern
kann das · Zeichen weggelassen werden.
Zwischen 2 Zahlen die durch eine Multiplikation
verknüpft sind muss immer ein · Zeichen gesetzt werden.
ALGEBRA 2
ALGEBRA 2
Um kompliziertere Terme zu verstehen, musst du Abmachungen kennen:
Was in Klammern steht, rechne zuerst.
(6+2): (7-3) = 8 :4 = 2
In klammerlosen Termen führe
zuerst das Potenzieren aus,
dann die Punktoperationen (. und :),
dann die Strichoperationen (+ und -).
3 · 52 - 8 : 4 = 3 · 25 - 8 : 4
= 75 - 2
= 73
Enthält ein klammerloser Term nur
Strichoperationen oder nur Punktoperationen, dann rechne der Reihe
nach von links nach rechts.
8-5+2 =3+2
8: 5· 2
= 1,6 · 2
=5
= 3,2
Terme mit Buchstaben können wir als Programme auffassen.
Der Term s
meint: Wähle eine beliebige Zahl.
Der Term a3- a
meint: Zähle eine Zahl von ihrer dritten Potenz ab.
Der Term 2. (x - y) meint: Verdopple die Differenz zweier Zahlen.
Wenn nichts Besonderes vermerkt ist, darfst du an die Stelle eines Buchstabens jede Zahl setzen, mit der du rechnen kannst.
Vorläufig sind dies alle positiven Zahlen und null, das heisst alle Zahlen
der Menge Q0+
Um kompliziertere Terme zu verstehen, musst du Abmachungen kennen:
Was in Klammern steht, rechne zuerst.
(6+2): (7-3) = 8 :4 = 2
In klammerlosen Termen führe
zuerst das Potenzieren aus,
dann die Punktoperationen (. und :),
dann die Strichoperationen (+ und -).
3 · 52 - 8 : 4 = 3 · 25 - 8 : 4
= 75 - 2
= 73
Enthält ein klammerloser Term nur
Strichoperationen oder nur Punktoperationen, dann rechne der Reihe
nach von links nach rechts.
8-5+2 =3+2
8: 5· 2
= 1,6 · 2
=5
= 3,2
Terme mit Buchstaben können wir als Programme auffassen.
Der Term s
meint: Wähle eine beliebige Zahl.
Der Term a3- a
meint: Zähle eine Zahl von ihrer dritten Potenz ab.
Der Term 2. (x - y) meint: Verdopple die Differenz zweier Zahlen.
Wenn nichts Besonderes vermerkt ist, darfst du an die Stelle eines Buchstabens jede Zahl setzen, mit der du rechnen kannst.
Vorläufig sind dies alle positiven Zahlen und null, das heisst alle Zahlen
der Menge Q0+
ALGEBRA 3
ALGEBRA 3
Die 4 Grundoperationen
Die 4 Grundoperationen
Addition
Addition
Merksatz:
Die Zahl vor einem Buchstabenterm heisst
Koëffizient ! (Achtung Ausnahme : Die Ziffer 1
als Koëffizient wird nicht geschrieben !)
Merksatz:
Die Zahl vor einem Buchstabenterm heisst
Koëffizient ! (Achtung Ausnahme : Die Ziffer 1
als Koëffizient wird nicht geschrieben !)
Beispiele:
1a + 2a + 3a = 6a
Beispiele:
1a + 2a + 3a = 6a
2a + 3b
Merke: nur gleiche Buchstaben können addiert
werden.
a und b's können nicht
addiert werden.
Als richtiges Beispiel gilt:
2a + 2b + 3a + 3b = 5a + 5b
Als richtiges Beispiel gilt:
2a + 2b + 3a + 3b = 5a + 5b
Subtraktion
Beispiele:
2a + 3b
Merke: nur gleiche Buchstaben können addiert
werden.
a und b's können nicht
addiert werden.
Subtraktion
5a - 2a - a = 2a
Merke: nur gleiche Buchstaben können subtrahiert
werden.
3a - 2b
a und b's können nicht
subtrahiert werden.
Als richtiges Beispiel gilt:
5a - 3b - 2a +5b = 3a + 2b
Beispiele:
5a - 2a - a = 2a
Merke: nur gleiche Buchstaben können subtrahiert
werden.
3a - 2b
a und b's können nicht
subtrahiert werden.
Als richtiges Beispiel gilt:
5a - 3b - 2a +5b = 3a + 2b
ALGEBRA 4
ALGEBRA 4
Die 4 Grundoperationen
Die 4 Grundoperationen
Multiplikation
Multiplikation
Beispiele:
a·a
= a2
5a · a
= 5a2
Buchstaben mal sich selber
= das Quadrat davon !
Die Koëffizienten werden
auch miteinander multipliziert
also 5 mal 1 = 5
a·a
= a2
5a · a
= 5a2
Buchstaben mal sich selber
= das Quadrat davon !
Die Koëffizienten werden
auch miteinander multipliziert
also 5 mal 1 = 5
3a · 3a = 9a2
Zahl mal Zahl und Buchstabe
mal Buchstabe
3a · 3a = 9a2
Zahl mal Zahl und Buchstabe
mal Buchstabe
a·b
Buchstaben können nicht
miteinander verwertet
werden; die Darstellung ist
eine Multiplikation.
a·b
Buchstaben können nicht
miteinander verwertet
werden; die Darstellung ist
eine Multiplikation.
= ab
Division
Beispiele:
Beispiele:
= ab
Division
15a : 3a
=5
denn 5 · 3a = 15a
Division : Zahl durch Zahl,
Buchstabe durch Buchstabe
2b : 5
= 0,4b
x3 : x
12y4 : 3y
Beispiele:
15a : 3a
=5
denn 5 · 3a = 15a
Division : Zahl durch Zahl,
Buchstabe durch Buchstabe
Division: Zahl durch Zahl,
Buchstabe durch 1
2b : 5
= 0,4b
Division: Zahl durch Zahl,
Buchstabe durch 1
= x2
denn x · x2 = x3
x3 : x
= x2
denn x · x2 = x3
= 4y3
denn 3y · 4 · y · y · y = 12y4
12y4 : 3y
= 4y3
denn 3y · 4 · y · y · y = 12y4
ALGEBRA 5
ALGEBRA 5
1. Kommutativgesetz (= Vertauschungsgesetz)
Dieses Gesetz gilt bei den Grundoperationen für Addition und
Multiplikation, nicht aber für Subtraktion, Division, Potenzieren und
Radizieren. Es erlaubt eine Umstellung der Summanden, bzw. der Faktoren.
1. Kommutativgesetz (= Vertauschungsgesetz)
Dieses Gesetz gilt bei den Grundoperationen für Addition und
Multiplikation, nicht aber für Subtraktion, Division, Potenzieren und
Radizieren. Es erlaubt eine Umstellung der Summanden, bzw. der Faktoren.
Beispiele:
7 + 5 = 5 + 7 = 12
5 • 9 = 9 • 5 = 45
aber:
7-5≠5-7
allgemein:
allgemein:
8: 4 ≠ 4: 8
a+b
a•b
=b+a
= b•a = ab
43 ≠ 34
2. Assoziativgesetz (Verbindungsgesetz)
Dieses Gesetz gilt bei den Grundoperationen für Addition und
Multiplikation, nicht aber für Subtraktion, Division, Potenzieren und
Radizieren. Es erlaubt, aus + und • Rechnungen beliebig Teilrechnungen
(Teilsummen bzw. Teilprodukte) zu bilden (Summanden bzw. Faktoren
beliebig zu verbinden).
Beispiele:
7 + 5 = 5 + 7 = 12
5 • 9 = 9 • 5 = 45
aber:
7-5≠5-7
allgemein:
allgemein:
8: 4 ≠ 4: 8
a+b
a•b
43 ≠ 34
2. Assoziativgesetz (Verbindungsgesetz)
Dieses Gesetz gilt bei den Grundoperationen für Addition und
Multiplikation, nicht aber für Subtraktion, Division, Potenzieren und
Radizieren. Es erlaubt, aus + und • Rechnungen beliebig Teilrechnungen
(Teilsummen bzw. Teilprodukte) zu bilden (Summanden bzw. Faktoren
beliebig zu verbinden).
Beispiele:
7 + 8 + 4 = (7+8) + 4 = 7 + (8+4) = 19
4 • 6 • 5 = (4 • 6) • 5 = 4 • (6 • 5) = 120
Beispiele:
7 + 8 + 4 = (7+8) + 4 = 7 + (8+4) = 19
4 • 6 • 5 = (4 • 6) • 5 = 4 • (6 • 5) = 120
allgemein:
a+b+c = (a+b)+c = a+(b+c)
a•b•c = (a•b)•c = a•(b•c)
allgemein:
a+b+c = (a+b)+c = a+(b+c)
a•b•c = (a•b)•c = a•(b•c)
aber:
12 - (5 - 3) ≠ (12 - 5) -3
aber:
12 - (5 - 3) ≠ (12 - 5) -3
(24: 6): 2 ≠ 24: (6: 2)
3. Distributivgesetz ( Verteilungsgesetz )
Dieses Gesetz erlaubt uns, Punkt- (•, :) und Strichoperationen (+, -)
miteinander zu verknüpfen . Es ist im mündlichen Rechnen und in der
Algebra sehr wichtig.
=b+a
= b•a = ab
(24: 6): 2 ≠ 24: (6: 2)
3. Distributivgesetz ( Verteilungsgesetz )
Dieses Gesetz erlaubt uns, Punkt- (•, :) und Strichoperationen (+, -)
miteinander zu verknüpfen . Es ist im mündlichen Rechnen und in der
Algebra sehr wichtig.
Beispiele:
5 • 38 = 5 • (30 + 8) = 5 • 30 + 5 • 8 = 150 + 40 = 190
7 • 79 = 7 • (80 - 1) = 7 • 80 - 7 • 1 = 560 - 7 = 553
Beispiele:
5 • 38 = 5 • (30 + 8) = 5 • 30 + 5 • 8 = 150 + 40 = 190
7 • 79 = 7 • (80 - 1) = 7 • 80 - 7 • 1 = 560 - 7 = 553
allgemein:
a•(b + c) = a•b + a•c = ab + ac
a•(b - c) = a•b - a•c = ab - ac
allgemein:
a•(b + c) = a•b + a•c = ab + ac
a•(b - c) = a•b - a•c = ab - ac
oder:
592: 8 = (560+32) : 8 = 560 : 8+32 : 8=70+4 = 74
364: 13 = (390-26): 13 = 390: 13 - 26: 13 = 30 - 2 = 28
oder:
592: 8 = (560+32) : 8 = 560 : 8+32 : 8=70+4 = 74
364: 13 = (390 - 26): 13 = 390: 13 - 26: 13 = 30 - 2 = 28
allgemein:
(a + b): c = a: c + b: c
(a - b): c = a: c - b: c
allgemein:
(a + b): c = a: c + b: c
(a - b): c = a: c - b: c
TEST 7.8.1 :
Termgewinnung
1. Schreibe als Zahlenterm und rechne ihn aus:
a)
subtrahiere von 7 das Doppelte von 3,8
b)
addiere zu 21 die Differenz von 1,8 und 0,7
c)
dividiere das Produkt von 4 und 5 durch 3
2. Übersetze den Zahlenterm in Worte und rechne aus
(16 - 9) : 2 =
3. Gewinne einen Zahlenterm ohne ihn auszurechnen:
Peter kauft für 13 Franken Marken : 18 Fünfzigermarken, für den Rest Achtzigermarken. Wieviele 80-er Marken erhält er ?
4. Erfinde aus dieser Aufgabe 3 verschiedene Aufgaben und gewinne aus ihnen
Zahlenterme:
a-c
Fredi und Susanne verdienen zusammen 870 Fr. Der Winterhilfe
schicken sie 120 Fr. den Rest halbieren sie; so bekommt jedes 375 Fr.
TEST 7.8.2 : gleichwertige Terme
1.
Zeichne 5 verschieden grosse Rechtecke, deren Länge um 2 Häuschen länger
ist als die Breite. Zähle wieviele Häuschen von innen an den Rand des Rechteckes stossen.
a)
stelle Deine Ergebnisse in einer Tabelle zusammen
b)
Überprüfe, ob folgende Formeln stimmen:
F1: 4a
F4:
a· (a+2) - a· (a-2)
F2: 2· (a+2) + 2a - 4
F5:
2a + 2· (a+2)
F3: 2· (a+1) + 2· (a-1)
2.
Wähle eine beliebige positive Zahl, addiere 2,5 ; multipliziere mit 2 und subtrahiere 5
a)
schreibe die Vorschrift mit einer Variablen auf
b)
setze anstelle der Variablen die Zahlen 0
0,8
1 2,5 3
und erstelle eine Wetetabelle
c)
suche einen einfacheren Term, der die gleichen Werte liefert.
3.
Vereinfache folgende Terme:
a)
n+n+n
b)
n–n–n–n
c)
d)
(n+1)· n – n · n
n:n:n
Lösungen:
TEST 7.8.1
1. Schreibe als Zahlenterm und rechne ihn aus:
a)
7 - 2 * 3,8 = - 0,6
b)
21 + ( 1,8 - 0,7 ) = 22,1
c)
( 4 * 5 ) : 3 = 6,666...
1 Pt
1Pt
1 Pt
2. Übersetze den Zahlenterm in Worte und rechne aus
(16 - 9) : 2 = 3,5 Halbiere die Differenz von 16 und 9
3. Gewinne einen Zahlenterm ohne ihn auszurechnen:
[ 1300 - ( 18 * 50 ) ] : 80 =
4. Erfinde aus dieser Aufgabe 3 verschiedene Aufgaben
und gewinne aus ihnen Zahlenterme:
a)
2 * 375 + 120 = 870
b)
870 - ( 2* 375) = 120
c)
870 - 120
= 2 * 375
Lösungen:
1a)
1b)
2
3
4
5
6
a
am Innenrand
8
12
16
20
24
2·(a+2)+2·(a-2)
richtig
falsch
1Pt
Farbe
8
rot
7
blau
6
blau
5
blau
4
gelb
3
gelb
2
gelb
1
gelb
0
gelb
Pt
Farbe
8
rot
7
blau
6
blau
1Pt
1Pt
1Pt
TEST 7.8.2
Breite
F1:
F3:
1Pt
Pt
F2:
F4:
richtig
falsch
F5:
2a)
(x + 2,5)·2 - 5
2b)
Zahl
0
0.8
1
2.5
3
Wert
0
1.6
2
5
6
2c)
3a)
2x
3n
3c)
3b)
–2n
3d)
1n
1/
n
falsch
5
blau
4
gelb
3
gelb
2
gelb
1
gelb
0
gelb
TEST 7.8.3
Der Gebrauch des Taschenrechners ist nicht gestattet
Vereinfache:
1.
g + 4g + g =
2.
11 e + 20e + 9e =
3.
3n + 6n + 9n =
4.
m + 2m - 3m + m + 6m =
Addiere, indem du die Summanden zweckmässig vertauschest und zusammenfassest.
5.
37 + 42 + 13 + 58 =
6.
59a + 24a + 47a + a + 16a =
7.
33p + 44p + 55p + 66p + 77p =
8.
18 + 16 + 14 + 12 - 10 - 8 - 6 - 4 - 2 =
TEST 7.8.4
Berechne möglichst einfach:
1.
2.
3.
4.
5.
6.
7.
8.
4 · 37 · 25
8 · 19,73 · 12,5
3 · 4x · 5
4z · 1 · 9
2 · 47 · 5 w
48x : 6x
7a : 4
(4 · 5a - 2a) : ( 3 · 2a)
=
=
=
=
=
=
=
=
Lösungen:
1.
6g
2.
40e
3.
18n
4.
7m
5.
150
6.
147a
7.
275p
8.
30
Lösungen:
1. 3700
2. 1973
3. 60x
4. 36z
5. 470w
6. 8
7. 7/4 x
8. 18a : 6a = 3
TEST 7.8.3
Pt
Beurteilung
8
7
6
5
4
3
2
1
0
rot
blau
blau
gelb
gelb
gelb
gelb
gelb
gelb
TEST 7.8.4
Pt
Beurteilung
8
7
6
5
4
3
2
1
0
rot
blau
blau
gelb
gelb
gelb
gelb
gelb
gelb
TEST 7.8.5
Schreibe als Produkt mit möglichst vielen Faktoren:
1.
12 z2
Vereinfache
2.
3.
4.
5.
6.
7.
8.
9.
x2 · x · 2x
3y · 4y2 · y3 =
=
3a2 · 0 · 4a
2x2 · 3x3 · 4x4 =
5y3 : 5y2
=
12 z8 : 2 z2
9v9 : 3v3
25u10 : 5u5
=
=
=
=
Kontrolliere folgende Umformung auf ihre Gültigkeit, indem du anstelle der Variablen
nacheinander die Zahlen 2; 1 und 1/2 einsetzest
10.
4a2 : 2a = 2a
TEST 7.8.6
1.
2.
Bilde die Summe, die Differenz, das Produkt und den Quotienten von
12 a und 6a
vereinfache:
6a · 3a2 · 4a
=
3.
vereinfache:
4.
5.
6.
7.
8.
2x3 - 5x3 + 7x3
=
2
Mit welcher Operation gelangt man vom Term 5x zum Term 35x5
Mit welcher Operation gelangt man vom Term 12a2 zum Term 3
Bestimme den Wert für den Term 4x3 wenn x = 1/2
Vereinfache Schritt für Schritt:
4a · 3a - 5a · 3a
=
Vereinfache Schritt für Schritt:
(2x3) 2 : (3x - x)2
=
Lösungen: TEST 7.8.5
1.
2.
3.
4.
5.
6.
2· 2·3·z·z
2x4
12y6
0
24x9
y
8.
6z6
3v6
9.
5u5
10.
4·4 :4
4·1 :2
4 ·1/4 : 1
7.
=4
=2
=1
Lösungen:
1.
2.
3.
4.
12a + 6a
12a - 6a
= 18 a
= 6a
12a · 6a
12a : 6a
72a4
= 72 a2
= 2
4x3
· 7x3
7.
: 4a2
0,5
- 3a2
8.
x4
5.
6.
ok.
ok
ok
Pt
Beurteilung
10
9
8
7
6
5
4
3
2
1
rot
blau
blau
blau
gelb
gelb
gelb
gelb
gelb
gelb
Pt
Beurteilung
8
7
6
5
4
3
2
1
0
rot
blau
blau
gelb
gelb
gelb
gelb
gelb
gelb
TEST 7.8.6
7.8.1 M-Lernkontrolle
Name: .................................................................
Reihe A
1. Schreibe als Zahlenterm und rechne aus.
a. Subtrahiere von 4 das Dreifache von1,5.
b. Dividiere die Summe von 1,2 und 0,3
durch 2.
c. Multipliziere das Produkt von 4 und 5 mit
dem Quotienten der beiden Zahlen.
2. Übersetze die Terme in Worte und rechne
aus.
24 – 8 : 2
(24 – 8) : 2
(12 – 4) · (8+2)
3. Gewinne Zahlenterme, ohne sie auszurechnen.
a. Auf einer Rolle sind 20 m Tuch.
Ein Viertel davon wird abgeschnitten.
Wieviel bleibt auf der Rolle?
b. Köbi kauft für 5 Fr. Marken: 12 Zwanzigermarken, für den Rest Zehnermarken.
Wie viele Zehnermarken erhält er?
c. Ein Fass enthält 90Liter Most. Die Hälfte
davon wird in 5-dl-Flaschen abgefüllt.
Wie viele 5-dl-Flaschen sind nötig?
:.
4. Schreibe mit Variablen.
Wähle eine Zahl, zähle 6 dazu, verdopple
das Ergebnis und subtrahiere schliesslich
die gewählte Zahl.
5. Schreibe in Worten:
a. 10 – a · 2
b. (10 - a) · 2
6. Setze in beiden Termen anstelle der Variablen die Zahlen 0; 1; 3/4 ; 1,2 und rechne. Tabelle!
a. 2 · a – 4
b. (2 – a) · a
a
0
1
3
/4
1,2
7. Wann nimmt der Term 16 – 4 · x
die folgenden Werte an?
a. 4
b. 6
2·a–4
(2 – a) · a
7.8.1 M-Lernkontrolle
Name: ................................................................
Reihe B
1. Schreibe als Zahlenterm und rechne
aus.
a. Subtrahiere 6 vom Dreifachen von 1,5.
b. Dividiere das Produkt von 1,2 und 3
durch 2.
c. Multipliziere die Summe von 4 und 8 mit
dem Quotienten der beiden Zahlen.
2. Übersetze die Terme in Worte und
rechne aus:
24 : 8 – 2
24: (8 - 2)
(12 · 4) – (8+2) .
3. Gewinne Zahlenterme, ohne sie auszurechnen.
a. In einem Fass hat es 80 Liter Most.
Ein Viertel davon wird abgezapft.
Wieviel bleibt im Fass ?
b. Vera wechselt 6 Fr. um: sie erhält
12 Zwanziger, für den Rest Zehner.
Wie viele Zehner erhält sie?
c. Eine Latte misst 8 m. Die Hälfte
wird in Stücke zu je 50 cm zersägt.
Wie viele 50-cm-Stücke gibt es?
4. Schreibe mit Variablen.
Wähle eine Zahl, subtrahiere 1, vervierfache das Ergebnis und addiere
schliesslich die gewählte Zahl.
5. Schreibe in Worten:
a. 5 – a · 3
c. (5 – a) · 3
6. Setze in beiden Termen anstelle der
Variablen die Zahlen 0; 1; 3/4 ; 1,2 und
rechne. Tabelle!
a. a · (2 – a)
b. 2 · a – 3
a
0
1
3
/4
1,2
7. Wann nimmt der Term 14 – 4 · x die
folgenden Werte an ?
a. 6
b. 4
a · (2 – a)
2·a–3
7.8.1 M-Resultate
7.8.1 M-Resultate
Reihe A
4.
5.
6.
7.
Reihe B
4.
5.
6.
7.
Mathplan 7.8.2
Algebra :
Name:
a
Termumformungen I I
b
Hilfsmittel :
Algebra 1
Zeitvorschlag:
2 Wochen
von:
am:
Lernkontrolle
1. Grobziele:
2. Hilfen:
3. Arbeitstempo:
c
a
c
b b
bis
Du sollst Dich über die wichtigsten Gesetze (Regelheft zur Termumformung)
wieder ins Bild setzen. Dies ist die Grundlage für Deine Arbeit.
erst wenn ich mich bemüht habe und trotzdem nicht klar komme, hole ich mir
Hilfe (mit dem bereits Gezeichneten und Berechneten als Grundlage.) Hilfe holen ist keine Schande !
Ich darf in meinem Tempo arbeiten (nicht trödeln).Die Zeit ist knapp berechnet. Für Sekundarschüler : Auswahl A (mindestens die fett gedruckten Nummern)
4. Hausaufgaben:
pro Woche 45 Minuten Weiterarbeit am Arbeitsplan > grün umranden
und das Datum und die Zeit dazu setzen !
5. Selbstbeurteilung:
Ich korrigiere meine Übungsaufgaben selber und benutze die Tests, um mein
Können zu überprüfen. Ich trage meine Ergebnisse in die Liste FORMATIVE
BEURTEILUNG ein !
Selbstbeurteilung auf der Rückseite eintragen
6. Auswertung:
7. Übersicht:
LP 95
Themenfeld
Anzahl
Wochen
Hilfsmittel
7.7
G: Quader
2
G1/S1
7.8.1
A : Arithmetik/Algebra : Termumformungen I
3
A1
7.8.2
A : Arithmetik/Algebra : Termumformungen II
2
A1
7.9
S: Prozentrechnung
3
S 1/ P 7
7.10
A: Algebra: Gleichungen und Ungleichungen
3
A1/S1
Inhalte, Begriffe, Hilfsmittel
Auswahl A
Auswahl B
Terme mit Zahlen und Variablen
über Q + ° mit mehreren Var.
A1: 411, 413, 415, 416, 417,
A1: 412, 414, 419
Terme auswerten
A1: 421, 422, 423, 424, 425
Zusammenfassung
418
A1: 426, 427
Test 7.8.7
Termumformungen
Vereinfachen von Produkten,
Operieren mit Produkten
A1: 511, 512, 513, 514, 515,
516, 518, 519
A1: 517, 5101, 5102,
5103, 5104, 5105
Vereinfachen von Summen und
Differenzen
A1: 521, 522, 523, 524, 525,
526, 527, 528, 529
A1: 5201, 5202, 5203,
5204, 5205
Test 7.8.8
Operieren mit Summen und
Differenzen
A1: 531, 532, 533
A1: 534, 535, 536, 536,
537, 538, 5301,
5302, 5303, 5304,
Vermischte Aufgaben
A1: 541, 542, 543, 544, 545,
546, 547
A1: 5401, 5402, 5403,
5404, 5405, 5406,
5407 5408
Test 7.8.9
Zusammenfassung
Lernkontrolle 7.8.3
Selbstbeurteilung:
Der Lehrer:
Die Eltern:
Bearbeitet am:
ALGEBRA 4
ALGEBRA 4
Die 4 Grundoperationen
Die 4 Grundoperationen
Multiplikation
Multiplikation
Beispiele:
a·a
= a2
5a · a
= 5a2
Buchstaben mal sich selber
= das Quadrat davon !
Die Koëffizienten werden
auch miteinander multipliziert
also 5 mal 1 = 5
a·a
= a2
5a · a
= 5a2
Buchstaben mal sich selber
= das Quadrat davon !
Die Koëffizienten werden
auch miteinander multipliziert
also 5 mal 1 = 5
3a · 3a = 9a2
Zahl mal Zahl und Buchstabe
mal Buchstabe
3a · 3a = 9a2
Zahl mal Zahl und Buchstabe
mal Buchstabe
a·b
Buchstaben können nicht
miteinander verwertet
werden; die Darstellung ist
eine Multiplikation.
a·b
Buchstaben können nicht
miteinander verwertet
werden; die Darstellung ist
eine Multiplikation.
= ab
Division
Beispiele:
Beispiele:
= ab
Division
15a : 3a
=5
denn 5 · 3a = 15a
Division : Zahl durch Zahl,
Buchstabe durch Buchstabe
2b : 5
= 0,4b
x3 : x
12y4 : 3y
Beispiele:
15a : 3a
=5
denn 5 · 3a = 15a
Division : Zahl durch Zahl,
Buchstabe durch Buchstabe
Division: Zahl durch Zahl,
Buchstabe durch 1
2b : 5
= 0,4b
Division: Zahl durch Zahl,
Buchstabe durch 1
= x2
denn x · x2 = x3
x3 : x
= x2
denn x · x2 = x3
= 4y3
denn 3y · 4 · y · y · y = 12y4
12y4 : 3y
= 4y3
denn 3y · 4 · y · y · y = 12y4
ALGEBRA 5
ALGEBRA 5
1. Kommutativgesetz (= Vertauschungsgesetz)
Dieses Gesetz gilt bei den Grundoperationen für Addition und
Multiplikation, nicht aber für Subtraktion, Division, Potenzieren und
Radizieren. Es erlaubt eine Umstellung der Summanden, bzw. der Faktoren.
1. Kommutativgesetz (= Vertauschungsgesetz)
Dieses Gesetz gilt bei den Grundoperationen für Addition und
Multiplikation, nicht aber für Subtraktion, Division, Potenzieren und
Radizieren. Es erlaubt eine Umstellung der Summanden, bzw. der Faktoren.
Beispiele:
7 + 5 = 5 + 7 = 12
5 • 9 = 9 • 5 = 45
aber:
7-5≠5-7
allgemein:
allgemein:
8: 4 ≠ 4: 8
a+b
a•b
=b+a
= b•a = ab
43 ≠ 34
2. Assoziativgesetz (Verbindungsgesetz)
Dieses Gesetz gilt bei den Grundoperationen für Addition und
Multiplikation, nicht aber für Subtraktion, Division, Potenzieren und
Radizieren. Es erlaubt, aus + und • Rechnungen beliebig Teilrechnungen
(Teilsummen bzw. Teilprodukte) zu bilden (Summanden bzw. Faktoren
beliebig zu verbinden).
Beispiele:
7 + 5 = 5 + 7 = 12
5 • 9 = 9 • 5 = 45
aber:
7-5≠5-7
allgemein:
allgemein:
8: 4 ≠ 4: 8
a+b
a•b
43 ≠ 34
2. Assoziativgesetz (Verbindungsgesetz)
Dieses Gesetz gilt bei den Grundoperationen für Addition und
Multiplikation, nicht aber für Subtraktion, Division, Potenzieren und
Radizieren. Es erlaubt, aus + und • Rechnungen beliebig Teilrechnungen
(Teilsummen bzw. Teilprodukte) zu bilden (Summanden bzw. Faktoren
beliebig zu verbinden).
Beispiele:
7 + 8 + 4 = (7+8) + 4 = 7 + (8+4) = 19
4 • 6 • 5 = (4 • 6) • 5 = 4 • (6 • 5) = 120
Beispiele:
7 + 8 + 4 = (7+8) + 4 = 7 + (8+4) = 19
4 • 6 • 5 = (4 • 6) • 5 = 4 • (6 • 5) = 120
allgemein:
a+b+c = (a+b)+c = a+(b+c)
a•b•c = (a•b)•c = a•(b•c)
allgemein:
a+b+c = (a+b)+c = a+(b+c)
a•b•c = (a•b)•c = a•(b•c)
aber:
12 - (5 - 3) ≠ (12 - 5) -3
aber:
12 - (5 - 3) ≠ (12 - 5) -3
(24: 6): 2 ≠ 24: (6: 2)
3. Distributivgesetz ( Verteilungsgesetz )
Dieses Gesetz erlaubt uns, Punkt- (•, :) und Strichoperationen (+, -)
miteinander zu verknüpfen . Es ist im mündlichen Rechnen und in der
Algebra sehr wichtig.
=b+a
= b•a = ab
(24: 6): 2 ≠ 24: (6: 2)
3. Distributivgesetz ( Verteilungsgesetz )
Dieses Gesetz erlaubt uns, Punkt- (•, :) und Strichoperationen (+, -)
miteinander zu verknüpfen . Es ist im mündlichen Rechnen und in der
Algebra sehr wichtig.
Beispiele:
5 • 38 = 5 • (30 + 8) = 5 • 30 + 5 • 8 = 150 + 40 = 190
7 • 79 = 7 • (80 - 1) = 7 • 80 - 7 • 1 = 560 - 7 = 553
Beispiele:
5 • 38 = 5 • (30 + 8) = 5 • 30 + 5 • 8 = 150 + 40 = 190
7 • 79 = 7 • (80 - 1) = 7 • 80 - 7 • 1 = 560 - 7 = 553
allgemein:
a•(b + c) = a•b + a•c = ab + ac
a•(b - c) = a•b - a•c = ab - ac
allgemein:
a•(b + c) = a•b + a•c = ab + ac
a•(b - c) = a•b - a•c = ab - ac
oder:
592: 8 = (560+32) : 8 = 560 : 8+32 : 8=70+4 = 74
364: 13 = (390-26): 13 = 390: 13 - 26: 13 = 30 - 2 = 28
oder:
592: 8 = (560+32) : 8 = 560 : 8+32 : 8=70+4 = 74
364: 13 = (390 - 26): 13 = 390: 13 - 26: 13 = 30 - 2 = 28
allgemein:
(a + b): c = a: c + b: c
(a - b): c = a: c - b: c
allgemein:
(a + b): c = a: c + b: c
(a - b): c = a: c - b: c
TEST 7.8.7
TEST 7.8.8
Vereinfache:
1. 2e2f · 6e2fg =
2. 3xyz2 : 0,6 yz =
3. (1/3 pq2 )2 =
4. 3a2 - 9a + 5a =
5. 3x3 + 2x2 + x + 6 + x2 + 6x + 3 =
6. 3a + 5 - 2a - 2a - 5 =
7. 2x2 - 4x2 - 2 - 2x + 1 + 3x + 3 - x2 =
8. 2x - 3y - z - 3x + 2y + x + 2y =
Lösungen:
TEST 7.8.7
1.
a · b – a2
2.
zum Beispiel :
Teile die Summe zweier Zahlen durch 3
3a.
u = 2b + 2c
3b.
A = a · b – c2
4
oder a · b – b2
Pt
Beurteilung
5
4
3
2
1
0
rot
blau
blau
gelb
gelb
gelb
Pt
Beurteilung
8
7
6
5
4
3
2
1
0
rot
blau
blau
gelb
gelb
gelb
gelb
gelb
gelb
zB.
b
b
a
a
a
b
a
a
a
5a.
Michael kauft a Tüten zu je b Franken. Wieviel
Herausgeld erhält er auf c Franken ?
5b.
c–a·b
[Fr.]
Lösungen: TEST 7.8.8
1.
2.
3.
4.
5.
6.
7.
8.
12e4f2g
5xz
1/ p2q4
9
3a2 – 4a
3x3 + 3x2 + 7x + 9
a
–3x2 + x + 2
y–z
TEST 7.8.9:
Vereinfachen
1. 0,6 a : 3
=
2. 4ab · 0,5 b
=
3. 8ax2 : 4ax : 2
=
4. 2pq – p · q
=
5. (4e · 2e )2 : (3e – e )3
=
6. 3 ( a+ b )2 – 2 ( a + b )2
=
7. AB - A - B
setze für A=2x und B=3x und vereinfache den Term
8. 2 ( x – y ) · 4 ( x – y ) : ( x – y )
Lösungen:
1.
2.
0,2 a
2ab2
3.
x
4.
pq
5.
64e4 : 8e3 = 8e
6.
(a + b)2
7.
6x2 – 2x – 3x = 6x2 – 5x
8.
8 (x – y)
=
TEST 7.8.9
Pt
Farbe
8
rot
7
blau
6
blau
5
blau
4
gelb
3
gelb
2
gelb
1
gelb
0
gelb
7.8.2 M-Lernkontrolle
Reihe A
Name:............................................................
7.8.2 M-Lernkontrolle
Reihe B
Name:...........................................................