Gaub-E1-7-2

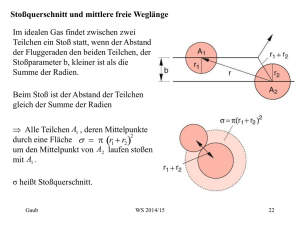
Stoßquerschnitt und mittlere freie Weglänge
Im idealen Gas findet zwischen zwei
Teilchen ein Stoß statt, wenn der Abstand
der Fluggeraden den beiden Teilchen, der
Stoßparameter b, kleiner ist als die
Summe der Radien.
Beim Stoß ist der Abstand der Teilchen
gleich der Summe der Radien
 Alle Teilchen A1 , deren Mittelpunkte
2
durch eine Fläche    r1  r2 
um den Mittelpunkt von A2 laufen stoßen
mit A1 .


σ heißt Stoßquerschnitt.

Gaub
WS 2014/15
22
Stoßquerschnitt und mittlere freie Weglänge
In einem dünnen Gas mit einer Dichte n von ruhenden Teilchen ist die
Wahrscheinlichkeit, dass ein einfliegendes Teilchen mit einem anderen auf der
Weglänge Δx wechselwirkt:
   n  x A  n  x
A
A
Bei N einlaufenden Teilchen stoßen
N  N n  x
dN

 n  dx
N
n  x
 N x   N 0 e
 N0 ex 
  1 / n
Mittlere freie
Weglänge
23
Stoßquerschnitt und mittlere freie Weglänge
Die mittlere Zeit τ zwischen 2 Stößen ist:
 

1

v
n v
Bewegen sich beide Teilchen, wird v durch die mittlere
Relativgeschwindigkeit 2 v 2 ersetzt:
 

1
n
2v 2

Typische Zahlen N2 bei Normaldruck: n ≈ 3 1021 / l,
Streuquerschnitt: ≈ 50 Å2
=> frei Weglänge ≈ 70 nm
Gaub
WS 2014/15
24
§7.4 Experimentelle Prüfung der kinetischen Gastheorie
Molekularstrahlen
Beim ausströmen eines dünnen Gases aus einem Reservoir, entsteht ein
gerichteter Strahl.
Für die Richtungsverteilung
gilt:
N   ~ cos 
Die Geschwindigkeitsverteilung
ist eine modifizierte MaxwellBoltzmann-Verteilung:
N v   n v f v 
tan 
b
2d
Die Blende B mit dem Durchmesser b
blendet den Winkelbereich    aus.


Kollimierter Molekülstrahl, d.h. alle Teilchen fliegen innerhalb des
Winkels ε zur Strahlachse.
25
Molekularstrahlen
Messung der Winkelverteilung der Moleküle durch einen schwenkbaren
Detektor.
Nach Einbau eines Geschwindigkeitsselektors, lässt sich die Anzahl der Teilchen
in einem vorgegebenen Geschwindigkeitsintervall messen.
Es können nur Teilchen die zweite Scheibe passieren, die zum Durchqueren des
Selektors so lange brauchen (Flugzeit T), wie Schlitz 2 um in die Position von
Schlitz 1 zu gelangen.
a ! 
a
T 


v 
v


Gaub
WS 2014/15
26
Molekularstrahlen
Das durchgelassene Geschwindigkeitsintervall Δv berechnet sich bei einer
Schlitzbreite S von S = R Δφ zu:
v  v
2 

Fehler im Demtröder! (Faktor 2 vergessen – unter der
Annahme, dass der 2. Schlitz genauso breit ist)
Durch die Variation von ω kann N(v) gemessen werden.
Entspricht n(v) der Maxwell-Boltzmann-Verteilung, folgt für N(v):
N v   nv  v 
Gaub
4v
vw3
3


e
m v2
2 kT
WS 2014/15
27
Molekularstrahlen
Um zu verhindern, dass Teilchen bei einem Winkel von 360° + φ die zweite
Scheibe durchqueren, werden mehrere Scheiben zwischengeschaltet.
Gaub
28
Molekularstrahlen
Prinzipien zum Nachweis von Molekülen in Molekularstrahlen:
Bolometer:
kinetische Energie der Moleküle
erwärmt Widerstand R
 Veränderung des elektrischen
Widerstands
R 
R
T
T
T 
N Ekin
G
Der Faktor G steht für die abgeleitete Wärme.
14
Möglichkeit zum Nachweis einer Leistung von 10 W .
Gaub
WS 2014/15

29
Molekularstrahlen
Prinzipien zum Nachweis von Molekülen in Molekularstrahlen:
Ionisationsdetektor:
Ionisation der einfallenden Teilchen
durch Elektronen
 Nachweis eines elektrischen
Stroms beim Aufsammeln der
Ionen
Erzeugter Strom bei Teilchenfluss N und einfacher Ionisation mit der
Ionisationswahrscheinlichkeit η:
I  Ne
Gaub
WS 2014/15
30
Molekularstrahlen
Prinzipien zum Nachweis von Molekülen in Molekularstrahlen:
Langmuir-Taylor- Detektor:
Ionisation der einfallenden Teilchen
an einem geheizten Draht

Nachweis der Ionen Durch Abziehen
mit einem elektrischen Feld
Ist die Ionisationsenergie der Teilchen kleiner als die Austrittsarbeit der
Elektronen aus dem Draht, wird bei diesem Übergang Energie frei.
Gaub
WS 2014/15
31
Molekularstrahlen
Prinzipien zum Nachweis von Molekülen in Molekularstrahlen:
moderne Methoden: laserspektroskotische Verfahren
Erhöhung des Drucks im Reservoir

mittlere freie Weglänge < Öffnung

Die Geschwindigkeiten der
Teilchen im Strahl gleichen sich
durch Stöße während der
Expansion an.
Die Geschwindigkeitsverteilung wird enger und die mittlere Geschwindigkeit
übersteigt die lokale Schallgeschwindigkeit („Überschallstrahl“).
Gaub
WS 2014/15
32
Molekularstrahlen
Strömungsgeschwindigkeit im Strahl:
N v   C v e
3

m u  v 2
2 k Tt
Mit der Translationstemperatur Tt als Maß für die Breite der
Geschwindigkeitsverteilung.
Tt kann kleiner als 1K werden!

Gaub
WS 2014/15
33