Lektion 5

Lektion 5
1
Stetige Verteilungen in R
In Lektion 1 haben Sie bereits die Log-Normalverteilung als ein Beispiel der in R implementierten
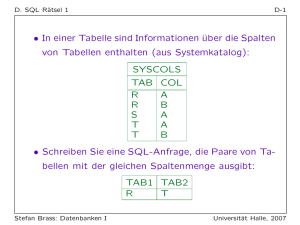
Verteilungen kennengelernt. Die neben dieser ebenfalls verfügbaren stetigen Verteilungen sind in der
untenstehenden Tabelle aufgeführt. Unter stetigen Verteilungen“ sollen dabei solche verstanden wer”
den, die eine stetige Verteilungsfunktion besitzen.
Name
Verteilung
auf
Parameter
Defaults
beta
Beta
[0, 1]
shape1, shape2, ncp
-, - , 0
cauchy
Cauchy
R
location, scale
0, 1
chisq
Chi-quadrat
R+
df, ncp
-, 0
exp
Exponential
R+
rate
1
f
F
R+
df1, df2, ncp
-, -, 0
gamma
Gamma
R+
shape, rate
-, 1
lnorm
Log-normal
R+
meanlog, sdlog
0, 1
logis
Logistische
R
location, scale
0, 1
norm
Normal
R
mean, sd
0, 1
t
Studentsche t
R
df, ncp
-, 0
unif
Gleichverteilung
[a, b]
min, max
0, 1
weibull
Weibull
R+
shape, scale
-, 1
Den Verteilungs-Kurznamen ist jeweils einer der Buchstaben d, p, q oder r voranzustellen. Mit d
erhalten Sie, wie schon in der ersten Lektion gesehen, den Wert der Dichte an der (den) Stelle(n)
x, mit p (probability) den Wert der zugehörigen Verteilungsfunktion. Mit q am Anfang erhalten Sie
die entsprechende Quantilfunktion, und mit r (random) können Sie eine Stichprobe unabhängiger,
identisch nach der jeweils gewählten Verteilung verteilter Zufallsvariablen erzeugen. Dabei gilt
Definition 1: Bei einer stetigen Verteilung V mit streng monoton wachsender Verteilungsfunktion
FV ist die zugehörige Quantilfunktion qV die Inverse von FV , d.h. qV : (0, 1) → R, qV (p) := FV−1 (p).
Für ein p-Quantil qV (p) von V gilt somit stets p = FV (qV (p)).
Bei vielen Verteilungen besitzen die zugehörigen Parameter Defaultwerte (vgl. dazu auch Lektion 2,
Seite 2). Beispielsweise ist bei Normalverteilungen stets der Mittelwert (mean) 0 und die Varianz 1
voreingestellt. So erhält man z.B. für Dichte und Verteilungsfunktion der Standard-Normalverteilung
an den Stellen ±1.6448536 die Werte
> dnorm(c(-1.6448536,1.6448536))
[1] 0.1031356 0.1031356
> pnorm(c(-1.6448536,1.6448536))
[1] 0.05 0.95
Da die Quantilfunktion gerade die Umkehrfunktion der Verteilungsfunktion ist, sind die 5%- und
95%-Quantile gegeben durch
1
c Math. Stochastik, Uni Freiburg
°
> qnorm(c(0.05,0.95))
[1] -1.644854 1.644854
Bei Änderung der Varianz von Normalverteilungen muss man in R etwas Vorsicht walten lassen:
Der zweite Verteilungsparameter sd (standard deviation) beschreibt nicht die Varianz, sondern deren
Wurzel! Die Wahrscheinlichkeit, dass eine normalverteilte Zufallsvariable mit Mittelwert 1 und Varianz
4 innerhalb des Intervalls [0, 3] liegt, berechnet sich daher in R wie folgt:
> pnorm(3,mean=1,sd=2)-pnorm(0,mean=1,sd=2)
[1] 0.5328072
Zum Vergleich von Dichte- und Quantilfunktion der Standard-Normalverteilung zeichnen wir beide
in einem gemeinsamen Plot. Dabei definieren wir, um Verzerrungen zu vermeiden, wie in der letzten
Lektion zunächst einen quadratischen Plotbereich.
> par(pty="s")
> x <- seq(-2,2,0.01)
> plot(x,pnorm(x),type="l",col="blue",ylim=c(-2,2),xlab="x",ylab="",
main="Verteilungs- und Quantilfuntion von N(0,1)")
> lines(seq(0.02,0.98,0.01),qnorm(seq(0.02,0.98,0.01)),col="red")
Zur Verdeutlichung fügen wir noch die Asymptoten beider Kurven hinzu. Zum Zeichnen solcher
Geraden kann man den Befehl abline() einsetzen. Mit abline(a,b) wird eine Gerade der Form
y = a + bx gezeichnet, mit abline(h=y) eine zur x-Achse parallele (horizontale) Gerade durch y und
mit abline(v=x) analog eine Parallele zur y-Achse (Vertikale) durch x. Der unten verwendete optionale Parameter lty (line type) im abline()-Befehl bewirkt, dass die Linie gestrichelt wird. Dazu sind
in R fünf Strichmuster vordefiniert, die durch die Zahlen 2, . . . , 6 ausgewählt werden können (mit der
Defaulteinstellung lty=1 erhält man eine normale durchgezogene Linie, mit lty=0 wird die Zeichnung
der Linie unterdrückt; lty kann auch innerhalb von lines() verwendet werden).
> abline(h=c(0,1),lty=3)
> abline(v=c(0,1),lty=3)
Im Gegensatz zu den Normal- sind die Exponentialverteilungen nur auf R+ definiert. Der Verteilungsparameter λ hat in R den Namen rate und den Defaultwert 1. Einen Plot mit Dichte und
Verteilungsfunktion der Exp(2)-Verteilung kann man wie folgt erhalten:
> x <- seq(0,2.5,0.01)
> plot(x,dexp(x,rate=2),type="l",ylim=c(0,2.5),xlab="x",ylab="",col="orange",
main="Dichte und Verteilungsfunktion von Exp(2)")
> lines(x,pexp(x,rate=2),col="blue")
Auch hier kann man wiederum Verteilungs- und Quantilfunktion grafisch miteinander vergleichen. Da
die Verteilungsfunktion für x > 2 nur noch sehr langsam wächst, sollte der Argumentvektor für die
Quantilfunktion etwas feiner unterteilt werden, damit beide Graphen in etwa die gleiche Länge haben.
> plot(x,pexp(x,rate=2),type="l",ylim=c(0,2.5),xlab="x",ylab="",col="blue",
main="Verteilungs- und Quantilfunktion von Exp(2)")
> lines(seq(0,0.993,0.001),qexp(seq(0,0.993,0.001),rate=2),col="red")
> abline(h=1,v=1,lty=3)
> par(pty="m")
2
c Math. Stochastik, Uni Freiburg
°
2
Diskrete Verteilungen in R
Neben den im vorigen Abschnitt vorgestellten stetigen Verteilungen sind in R auch fünf diskrete
Verteilungen implementiert, nämlich die Binomialverteilung, die geometrische Verteilung, die Hypergeometrische Verteilung, die Poissonverteilung und die negative Binomial- oder Pascalverteilung. Die
jeweiligen Kurznamen und benötigten Parameter können Sie der folgenden Tabelle entnehmen:
Name
Verteilung
Parameter
binom
Binomial
size, prob
geom
Geometrische
prob
hyper
Hypergeometrische
m, n, k
pois
Poisson
lambda
nbinom
negative Binomial
size, prob
Die Parameter size und prob entsprechen bei der Binomialverteilung n und p, bei der Hypergeometrischen Verteilung ist m die Anzahl der z.B. weißen Kugeln in der Urne, n die Anzahl der schwarzen
und k die Anzahl der insgesamt gezogenen Kugeln.
Alle oben genannten Parameter haben keine Defaultwerte und müssen beim Aufruf der Verteilungen
(durch Voranstellen von d, p, q oder r wie zuvor beschrieben) explizit angegeben werden. Für die
Wahrscheinlichkeit, aus einer Urne mit 4 weißen und 6 schwarzen Kugeln bei drei Ziehungen ohne
Zurücklegen insgesamt höchstens eine weiße zu ziehen, erhält man beispielsweise
> phyper(1,4,6,3)
[1] 0.6666667
Bei den Dichte- und Verteilungsfunktionen der geometrischen Verteilung ist als erstes Argument anstelle der Wartezeit n bis zum ersten Erfolg eines Bernoulli-Experiments die Anzahl n − 1 der vorausgehenden Misserfolge anzugeben. Die Wahrscheinlichkeit, dass bei wiederholtem Werfen einer fairen
Münze spätestens im sechsten Wurf das erste Mal Kopf“ fällt, erhält man somit durch
”
> pgeom(5,0.5)
[1] 0.984375
Man beachte, dass alle o.g. Verteilungen nur Masse auf die natürlichen Zahlen (inklusive der Null)
legen; bei einer B(10, 0.4)-Verteilung erhält man z.B.
> dbinom(seq(0,2,0.5),10,0.4)
[1] 0.006046618 0.000000000 0.040310784 0.000000000 0.120932352
Warnmeldungen:
1: In dbinom(seq(0, 2, 0.5), 10, 0.4) : non-integer x = 0.500000
2: In dbinom(seq(0, 2, 0.5), 10, 0.4) : non-integer x = 1.500000
Anders ausgedrückt: Bei diskreten Verteilungen berechnen die zugehörigen Dichte“-Funktionen in R
”
die Elementarwahrscheinlichkeiten P (X = k), sofern die entsprechende Komponente des Argumentvektors eine natürliche Zahl k ist, und geben ansonsten Null zurück. Diese Besonderheiten sollten
auch bei der grafischen Darstellung berücksichtigt werden. Dichten diskreter Verteilungen stellt man
üblicherweise als Stabdiagramme dar, bei denen die einzelnen Punkte bzw. Zahlen, denen die betreffende Verteilung echt positive Gewichte zuordnet, durch Stäbe oder Linien markiert werden, deren
3
c Math. Stochastik, Uni Freiburg
°
Längen jeweils den genauen Wert der dort liegenden Wahrscheinlichkeiten angeben. Grafiken dieser
Art kann man in R durch Setzen der Plot-Option type="h" (histogram oder high density) erzeugen.
Damit lassen sich die Gewichte der B(10, 0.4)-Verteilung wie folgt visualisieren:
> plot(0:10,dbinom(0:10,10,0.4),type="h",col="red",xlab="k",ylab="",
main="Gewichte der B(10,0.4)-Verteilung")
Die Verteilungsfunktionen diskreter Verteilungen lassen sich als einfache Summe darstellen und berechnen. Genauer gesagt gilt die folgende
Definition 2: Sei G eine Verteilung, deren Gewichte g(xk ) = P (X = xk ) auf den Zahlen (xk )k≥0
liegen, für die x0 < x1 < x2 , . . . gelte. Dann ist die zugehörige Verteilungsfunktion FG gegeben durch
FG (x) :=
P
xk ≤x g(xk )
=
Pk∗
k=0 g(xk ),
wobei k ∗ = max{k ≥ 0 | xk ≤ x}.
Aus dieser folgt unmittelbar, dass die Verteilungsfunktionen diskreter Verteilungen stückweise konstant sind und ihren Wert nur durch Sprünge ändern. Die Sprunghöhe entspricht dabei jeweils dem an
der betreffenden Stelle liegenden Gewicht. Um solche Funktionen in R grafisch darzustellen, greifen
wir auf den Befehl segments(x0,y0,x1,y1) zurück, der innerhalb eines bestehenden Plots jeweils die
Punkte (x0[i], y0[i]) und (x1[i], y1[i]) durch Geradenstücke miteinander verbindet. Zur Erzeugung eines zunächst leeren Plots, in den man anschließend mit Hilfe von segments() die gewünschte
Verteilungsfunktion einzeichnen kann, muss die Option type="n" (nothing) gesetzt werden. Sie bewirkt, dass der plot()-Befehl lediglich anhand der Koordinatenvektoren die Achsen samt Beschriftung
generiert, eine (sichtbare) Ausgabe bzw. Markierung der angegebenen Punkte jedoch unterbleibt. Um
zu verdeutlichen, dass diese gemäß obiger Definition rechtsseitig stetig ist, fügen wir an den Sprungstellen zusätzlich einzelne Punkte hinzu.
> plot(0:12,pbinom(0:12,10,0.4),xlab="x",ylab="",type="n",
main="Verteilungsfunktion der B(10,0.4)-Verteilung")
> segments(0:11,pbinom(0:11,10,0.4),1:12,pbinom(0:11,10,0.4),col="blue")
> points(0:10,pbinom(0:10,10,0.4),pch=20,col="blue")
Die Quantilfunktion ist für diskrete Verteilungen wie folgt definiert:
Definition 3: Sei G eine Verteilung, deren Gewichte g(xk ) = P (X = xk ) auf den Zahlen (xk )k≥0
liegen, für die x0 < x1 < x2 , . . . gelte. Dann ist die zugehörige Quantilfunktion qG : (0, 1) → {xk , k ≥ 0}
gegeben durch qG (p) := inf{x | FG (x) ≥ p} = xl∗ , wobei l∗ = min{l ≥ 0 |
Pl
k=0 g(xk )
≥ p}.
Auch die Quantilfunktion diskreter Verteilungen ist somit eine stückweise konstante Sprungfunktion,
deren Sprungstellen innerhalb des Einheitsintervalls gerade den (endlich oder abzählbar vielen) verschiedenen Werten der zugehörigen Verteilungsfunktion entsprechen. Beim Plot der Quantilfunktion
kann man sich zunutze machen, dass diese auch bei diskreten Verteilungen in gewissem Sinn die Inverse
der Verteilungsfunktion ist und man daher das allgemeine Prinzip der Umkehrfunktion – vertausche x
und y – anwenden kann. Daher kann man die Quantilfunktion der B(10, 0.4)-Verteilung in R mit den
folgenden Befehlen zeichnen (man vergleiche dabei den untenstehenden segments()-Befehl mit dem
zum Plotten der Verteilungsfunktion verwendeten!):
> plot(c(0,1),c(0,10),type="n",xlab="p",ylab="",
main="Quantilfunktion der B(10,0.4)-Verteilung")
> segments(c(0,pbinom(0:9,10,0.4)),0:10,pbinom(0:10,10,0.4),0:10,col="red")
> points(pbinom(0:9,10,0.4),0:9,pch=20,col="red")
4
c Math. Stochastik, Uni Freiburg
°
Während die Binomialverteilungen B(n, p) ihre Gewichte lediglich auf die Zahlen 0, 1, . . . , n verteilen
und somit auch deren Quantilfunktionen nur diese Werte annehmen können, belegen geometrische und
Poisson-Verteilung ganz N ∪ {0} mit echt positiven Wahrscheinlichkeiten, so dass ihre Quantilfunktionen beliebig große Werte annehmen können. Wie man allerdings am Plot der Verteilungsfunktion
der Geom(0.5)-Verteilung erkennen kann, ist diese bei x = 9 schon sehr nahe an der 1 und steigt für
größere x nur noch sehr langsam an.
> plot(0:13,pgeom(0:13,0.5),type="n",xlab="x",ylab="",ylim=c(0,1),
main="Verteilungsfunktion der Geom(0.5)-Verteilung")
> segments(0:12,pgeom(0:12,0.5),1:13,pgeom(0:12,0.5),col="blue")
> points(0:12,pgeom(0:12,0.5),pch=20,col="blue")
Dies impliziert, dass sich die Sprünge der Quantilfunktion bei 1 häufen. Wegen
> qgeom(0.999,0.5)
[1] 9
genügt es aber, sich auf den Wertebereich von 0 bis 9 zu beschränken, um die Quantilfunktion zumindest über (0, 0.999) (statt (0, 1)) plotten zu können.
> plot(c(0,1),c(0,9),type="n",xlab="p",ylab="",
main="Quantilfunktion der Geom(0.5)-Verteilung")
> segments(c(0,pgeom(0:8,0.5)),0:9,pgeom(0:9,0.5),0:9,col="red")
> points(pgeom(0:8,0.5),0:8,pch=20,col="red")
3
Grenzwerte der Binomialverteilung – Teil I
In der Stochastik-Vorlesung haben Sie bereits den folgenden Satz von de Moivre-Laplace kennengelernt:
Satz 1 (de Moivre-Laplace) Sei (Xn )n≥1 eine Folge von unabhängigen, identisch verteilten Zufallsvariablen mit P (X1 = 1) = p = 1 − P (X1 = 0) und p ∈ (0, 1). Für beliebige a < b und
Sn∗ =
n
X
k=1
Xk − p
gilt dann
np(1 − p)
p
lim P (a < Sn∗ ≤ b) = Φ(b) − Φ(a)
n→∞
1
mit Φ(x) = √
2π
Z x
−∞
e−
y2
2
dy.
Setzt man a := −∞ und b = x, so besagt der Satz nichts anderes, als dass die Verteilungsfunktion der
standardisierten Summe Sn∗ gegen die Verteilungsfunktion der Standard-Normalverteilung konvergiert.
Dies soll mit den zuvor bereitgestellten Mitteln grafisch veranschaulicht werden. Wir beginnen mit
n = 20 und p = 0.4. Die nicht standardisierte Summe Sn ist dann B(20, 0.4)-verteilt und hat den
Erwartungswert E(S20 ) = 20 · 0.4 = 8 und die Varianz Var(S20 ) = 20 · 0.4 · 0.6 = 4.8. Die Gewichte der
Verteilung der standardisierten Summe Sn∗ entsprechen denen der B(20, 0.4)-Verteilung, liegen aber
auf den Zahlen xk =
k−8
√
,
4.8
0 ≤ k ≤ 20, anstatt auf 0, 1, . . . , 20. Die zugehörige Verteilungsfunktion
kann man daher wie folgt plotten:
> x <- ((0:21)-8)/sqrt(4.8)
> plot(c(-4,6),c(0,1),type="n",xlab="x",ylab="",
main="Standardisierte B(20,0.4)- und N(0,1)-Verteilung")
> segments(x[-22],pbinom(0:20,20,0.4),x[-1],pbinom(0:20,20,0.4),col="blue")
> points(x[-22],pbinom(0:20,20,0.4),pch=20,col="blue")
5
c Math. Stochastik, Uni Freiburg
°
Zum Vergleich legen wir nun noch die Verteilungsfunktion der Standard-Normalverteilung darüber.
> lines(seq(-4,6,0.01),pnorm(seq(-4,6,0.01)),col="red")
Eine weitere Möglichkeit, zwei Verteilungen F und G miteinander zu vergleichen, besteht in sogenannten Q-Q-Plots (Quantile-Quantile-Plots). Dabei werden für verschiedene p die p-Quantile von F gegen
diejenigen von G aufgetragen. Sind beide Verteilungen identisch, so auch ihre Verteilungsfunktionen
und mithin ihre Quantile. In diesem Fall liegen die Punkte (qF (p), qG (p)) genau auf der Winkelhalbierenden y = x, während sie bei F 6= G mehr oder weniger stark von dieser abweichen. Die Größe
der Abweichungen gibt einen qualitativen Eindruck darüber, ob und inwieweit beide Verteilungen
näherungsweise übereinstimmen.
Der Satz von de Moivre-Laplace impliziert, dass Q-Q-Plots mit Quantilen der Verteilung von Sn∗ gegen
die entsprechenden Quantile der N (0, 1)-Verteilung mit wachsendem n gegen die Winkelhalbierende
konvergieren. Da sich, wie oben angedeutet, beim Übergang von der B(n, p)-Verteilung zu derjenigen
von Sn∗ nur die Lage der Verteilungsgewichte ändert, aber nicht deren Werte, folgt aus Definition 3
unmittelbar, dass sich die Quantile vollkommen analog zu den Positionen der Gewichte transformieren:
∗ (p) =
Ist qB(20,0.4) (p) = k, so ist qS20
k−8
√
.
4.8
Somit kann man den entsprechenden Q-Q-Plot erstellen
durch
> plot(qnorm(seq(0.01,0.99,0.01)),(qbinom(seq(0.01,0.99,0.01),20,0.4)-8)/sqrt(4.8),
xlab="Quantile von N(0,1)",ylab="Quantile von standardisierter B(20,0.4)",
pch=20,main="Q-Q-Plot: Standardisierte B(20,0.4) gegen N(0,1)")
> abline(0,1)
Um die Normalverteilungskonvergenz für wachsendes n besser veranschaulichen zu können, benötigen
wir noch ein paar grafische Hilfsmittel, die im folgenden Abschnitt vorgestellt werden.
4
Mehrere Plots in einem Grafikfenster
Grafische Parameter können in R mit dem par()-Befehl gesetzt werden; die Syntax dazu lautet
par(Parameter1=Wert1,Parameter2=Wert2,...)
Ohne Argumente gibt par() eine Liste mit allen Parametern und deren momentanen Werten aus. Um
mehrere Plots in einem Fenster zeichnen zu können, müssen die Parameter mfrow (multiple figures per
row) oder mfcol verändert werden. Diese werden mit par(mfrow=c(m,n)) bzw. par(mfcol=c(m,n))
gesetzt. Wie bei einer m×n-Matrix definiert man damit m Zeilen mit jeweils n Plots nebeneinander. Bei
Verwendung von mfrow werden die verschiedenen Plots zeilenweise hinzugefügt, bei mfcol spaltenweise.
Mit den graphischen Parametern mar (margin) und oma (outer margin) kann die Fensteraufteilung
beeinflusst werden. Dies geschieht mit
par(mar=c(bottom,left,top,right)) bzw. par(oma=c(bottom,left,top,right))
Für bottom, left, top und right ist jeweils eine Zahl einzusetzen, die die Breite des zugehörigen Randes (Maßstab: eine Textzeile) angibt. Die Defaultwerte sind mar=c(5.1,4.1,4.1,2.1) und
oma=c(0,0,0,0) (kein äußerer Rand). Zum besseren Verständnis siehe auch die Skizzen auf Seite 7.
Randbeschriftungen können mit dem Befehl
mtext(text,side=3,line=0,outer=FALSE,adj=NA,cex=NA,col=NA)
eingefügt werden; dabei enthält die Zeichenkette text den gewünschten Text, side legt den Rand fest
6
c Math. Stochastik, Uni Freiburg
°
Outer Margin
margin 3
•
Margin for figure 1
•
Margin for figure 2
•
margin 2
Plot area
Plot area
for figure 1
for figure 2
margin 4
•
•
•
Plot
Figure
margin 1
Abbildung 1: Zur Definiton und Wirkung der graphischen Parameter mar und oma
(1 unten, 2 links, 3 oben, 4 rechts), line die Position der Textzeile (von innen nach außen, beginnend
bei 0), cex und col Textgröße und -Farbe. Mit outer=TRUE wird der Text in den äußeren Rand
geschrieben.
Um die Verteilungsfunktionen und Q-Q-Plots für p = 0.4 und n = 50, 100, 250 neben- bzw. untereinander zu plotten und einen oberen Rand für einen gemeinsamen Titel zu haben, setzen wir zunächst
> par(mfcol=c(3,2),oma=c(0,0,2,0))
und erstellen dann die einzelnen Plots. Zum Schluss sollten die Grafik-Parameter wieder auf die
Defaultwerte zurückgesetzt werden.
> x <- ((0:51)-50*0.4)/sqrt(50*0.4*0.6)
> plot(c(-4,6),c(0,1),type="n",xlab="",ylab="",main="n=50, p=0.4")
> segments(x[-52],pbinom(0:50,50,0.4),x[-1],pbinom(0:50,50,0.4),col="blue")
> lines(seq(-4,6,0.01),pnorm(seq(-4,6,0.01)),col="red")
> x <- ((0:101)-100*0.4)/sqrt(100*0.4*0.6)
> plot(c(-4,6),c(0,1),type="n",xlab="",ylab="",main="n=100, p=0.4")
> segments(x[-102],pbinom(0:100,100,0.4),x[-1],pbinom(0:100,100,0.4),col="blue")
> lines(seq(-4,6,0.01),pnorm(seq(-4,6,0.01)),col="red")
> x <- ((0:251)-250*0.4)/sqrt(250*0.4*0.6)
> plot(c(-4,6),c(0,1),type="n",xlab="",ylab="",main="n=250, p=0.4")
> segments(x[-252],pbinom(0:250,250,0.4),x[-1],pbinom(0:250,250,0.4),col="blue")
> lines(seq(-4,6,0.01),pnorm(seq(-4,6,0.01)),col="red")
> plot(qnorm(seq(0.01,0.99,0.01)),(qbinom(seq(0.01,0.99,0.01),50,0.4)-50*0.4)/
sqrt(50*0.4*0.6),pch=20,xlab="",ylab="",main="n=50, p=0.4")
> plot(qnorm(seq(0.01,0.99,0.01)),(qbinom(seq(0.01,0.99,0.01),100,0.4)-100*0.4)/
sqrt(100*0.4*0.6),pch=20,xlab="",ylab="",main="n=100, p=0.4")
> plot(qnorm(seq(0.01,0.99,0.01)),(qbinom(seq(0.01,0.99,0.01),250,0.4)-250*0.4)/
sqrt(250*0.4*0.6),pch=20,xlab="",ylab="",main="n=250, p=0.4")
> mtext("Konvergenz der B(n,p)-Verteilungen gegen N(0,1)",outer=TRUE)
> par(mfcol=c(1,1),oma=c(0,0,0,0))
7
c Math. Stochastik, Uni Freiburg
°
5
Grenzwerte der Binomialverteilung – Teil II
Neben der Normalverteilung kann als Grenzverteilung der Binomial- auch die Poissonverteilung auftreten. Dieser Sachverhalt wird beschrieben durch
Satz 2 (Poissons Gesetz der kleinen Zahlen) Sei 0 < λ < ∞ und (pn )n≥1 eine Folge von Zahlen
aus (0, 1) mit limn→∞ npn = λ, so gilt für alle 0 ≤ k < ∞:
µ ¶
lim
n→∞
n k
λk −λ
pn (1 − pn )n−k =
e .
k
k!
Auch diese Konvergenz soll mit den zuvor erarbeiteten Methoden veranschaulicht werden. Wir beginnen mit einer B(10, 0.3)-Verteilung und vergleichen deren Verteilungsfunktion mit der der Poissonverteilung zum Parameter λ = 10 · 0.3 = 3.
> plot(c(0,11),c(0,1),type="n",xlab="x",ylab="",
main="Vergleich von B(10,0.3) und Pois(3)")
> segments(0:10,pbinom(0:10,10,0.3),1:11,pbinom(0:10,10,0.3),col="blue")
> points(0:10,pbinom(0:10,10,0.3),pch=20,col="blue")
> segments(0:10,ppois(0:10,3),1:11,ppois(0:10,3),col="red")
> points(0:10,ppois(0:10,3),pch=20,col="red")
Den zugehörigen Q-Q-Plot erhält man durch folgenden Befehl:
> plot(qpois(seq(0.01,0.99,0.01),3),qbinom(seq(0.01,0.99,0.01),10,0.3),pch=20,
xlab="Quantile von Pois(3)",ylab="Quantile von B(10,0.3)",
main="Q-Q-Plot: B(10,0.3) gegen Pois(3)")
Abschließend untersuchen wir das Konvergenzverhalten gegen die Pois(3)-Verteilung für die Binomialverteilungen B(20, 0.15), B(50, 0.06) und B(100, 0.03) in einem gemeinsamen Plot.
> par(mfcol=c(3,2),oma=c(0,0,2,0))
> plot(c(0,10),c(0,1),type="n",xlab="",ylab="",main="n=20, p=0.15")
> segments(0:10,pbinom(0:10,20,0.15),1:11,pbinom(0:10,20,0.15),col="blue")
> segments(0:10,ppois(0:10,3),1:11,ppois(0:10,3),col="red")
> plot(c(0,10),c(0,1),type="n",xlab="",ylab="",main="n=50, p=0.06")
> segments(0:10,pbinom(0:10,50,0.06),1:11,pbinom(0:10,50,0.06),col="blue")
> segments(0:10,ppois(0:10,3),1:11,ppois(0:10,3),col="red")
> plot(c(0,10),c(0,1),type="n",xlab="",ylab="",main="n=100, p=0.03")
> segments(0:10,pbinom(0:10,100,0.03),1:11,pbinom(0:10,100,0.03),col="blue")
> segments(0:10,ppois(0:10,3),1:11,ppois(0:10,3),col="red")
> plot(qpois(seq(0.01,0.99,0.01),3),qbinom(seq(0.01,0.99,0.01),20,0.15),pch=20,
xlab="",ylab="",main="n=20, p=0.15")
> plot(qpois(seq(0.01,0.99,0.01),3),qbinom(seq(0.01,0.99,0.01),50,0.06),pch=20,
xlab="",ylab="",main="n=50, p=0.06")
> plot(qpois(seq(0.01,0.99,0.01),3),qbinom(seq(0.01,0.99,0.01),100,0.03),pch=20,
xlab="",ylab="",main="n=100, p=0.03")
> mtext("Konvergenz von B(n,p) gegen Pois(3)",outer=TRUE)
> par(mfcol=c(1,1),oma=c(0,0,0,0))
8
c Math. Stochastik, Uni Freiburg
°
6
Übungen
1. Falls log(X) eine nach N (µ, σ 2 )-verteilte Zufallsvariable ist, so nennt man die Verteilung von X
eine Log-Normalverteilung. In R ist deren Quantilfunktion mit qlnorm(x,meanlog=µ,sdlog=σ)
implementiert. Finden Sie eine Funktion h(x), die h(qnorm(x))==qlnorm(x) erfüllt.
2. Sei x <- seq(0,1,0.01). Gegeben seien auf [0, 1] uniform verteilte, unabhängige Zufallsvariablen U1 , ..., Un . Es ist bekannt, dass max1≤i≤n Ui Beta-verteilt ist mit Parametern shape1=n,
shape2=1. Interpretieren Sie das Ergebnis von
punif(x)^n - pbeta(x,n,1)
für beliebige n.
3. Interpretieren Sie das Ergebnis von pexp(-log(1-x))-punif(x).
Warum liefern die beiden Befehle
qexp(runif(1))
und
rexp(1)
und
rlogis(1)
(in Verteilung) dasselbe Ergebnis?
Gilt auch, dass die beiden Befehle
qlogis(runif(1))
in Verteilung dasselbe liefern?
4. Ergänzen Sie die in Lektion 2, Übungsaufgabe 7, eingeführte Verteilungsfamilie um eine Funktion
qv(p,alpha), die die p-Quantile qV (α); p von V (α) berechnet und ausgibt. Dabei sollte qv() für
p 6∈ [0, 1] mit einer Fehlermeldung abbrechen und alpha=1 als Defaultwert vorgegeben werden.
Zusatz : Erweitern Sie qv(p,alpha) so, dass auch vektorwertige Argumente p korrekt verarbeitet werden.
5. Sei x <- seq(0,1,0.001). Offenbar liefert
> mu <- 10
> sigma <- 144
> plot(qnorm(x,mean=0,sd=1), (qnorm(x,mean=mu,sd=sigma) - mu)/sigma,
xlab="Quantile von N(0,1)", ylab="Quantile von standardisierter
N(mu,sigma)", pch=20, main="")
eine Gerade. Warum liefert auch
> plot(qnorm(x,mean=0,sd=1), qnorm(x,mean=mu,sd=sigma), xlab="Quantile
von N(0,1)", ylab="Quantile von N(mu,sigma)", pch=20, main="")
eine Gerade?
6. Gegen welche Verteilung konvergieren die Binomialverteilungen B(n, pn ), falls entgegen den Annahmen von Satz 2 gilt, dass limn→∞ npn = 0? Welchen Wertebereich hat die zugehörige Quantilfunktion? Veranschaulichen Sie auch diesen Grenzfall durch Vergleiche der Verteilungsfunktionen
und Q-Q-Plots.
7. Seien X1 , X2 , ... hypergeometrisch verteilt, wobei Xi die Parameter mi , ni , und ki besitzt. (Das
bedeutet, dass man sich Xi als die Anzahl der gezogenen weißer Kugeln vorstellen kann, wenn
die Urne mi weiße Kugeln und ni andere Kugeln enthält, und ki Kugeln gezogen werden.)
9
c Math. Stochastik, Uni Freiburg
°
Sei pi :=
mi
mi +ni ,
limi→∞ ki = ∞, limi→∞ mi = ∞, limi→∞
ki
mi
= 0 und limi→∞ pi ∈ (0, 1). Wir
interessieren uns für die Konvergenz der Verteilungen, analog zum Satz von de Moivre-Laplace.
Raten Sie: Welche Funktion F (·) erfüllt
Ã
lim P
i→∞
!
Xi − ki pi
p
≤x
ki pi (1 − pi )
= F (x)
für alle x ∈ R? Ermitteln Sie den Grenzwert approximativ durch Plot der Verteilungsfunktionen
und Q-Q-Plots.
8. Exponentialapproximation der geometrischen Verteilung
Veranschaulichen Sie auch die folgende, aus der Stochastik-Vorlesung bekannte Verteilungskonvergenz mit Hilfe der in der Lektion vorgestellten Methoden.
Satz 3 Sei (Xn )n≥1 eine Folge geometrisch verteilter Zufallsvariablen mit Xn ∼ Geom(pn ) und
limn→∞ pn = 0. Dann gilt
lim P (a ≤ pn Xn ≤ b) = P (a ≤ Z ≤ b),
n→∞
wobei Z eine exponentialverteilte Zufallsvariable zum Parameter λ = 1 ist (Z ∼ Exp(1)).
10
c Math. Stochastik, Uni Freiburg
°