Schülerzirkel Mathematik

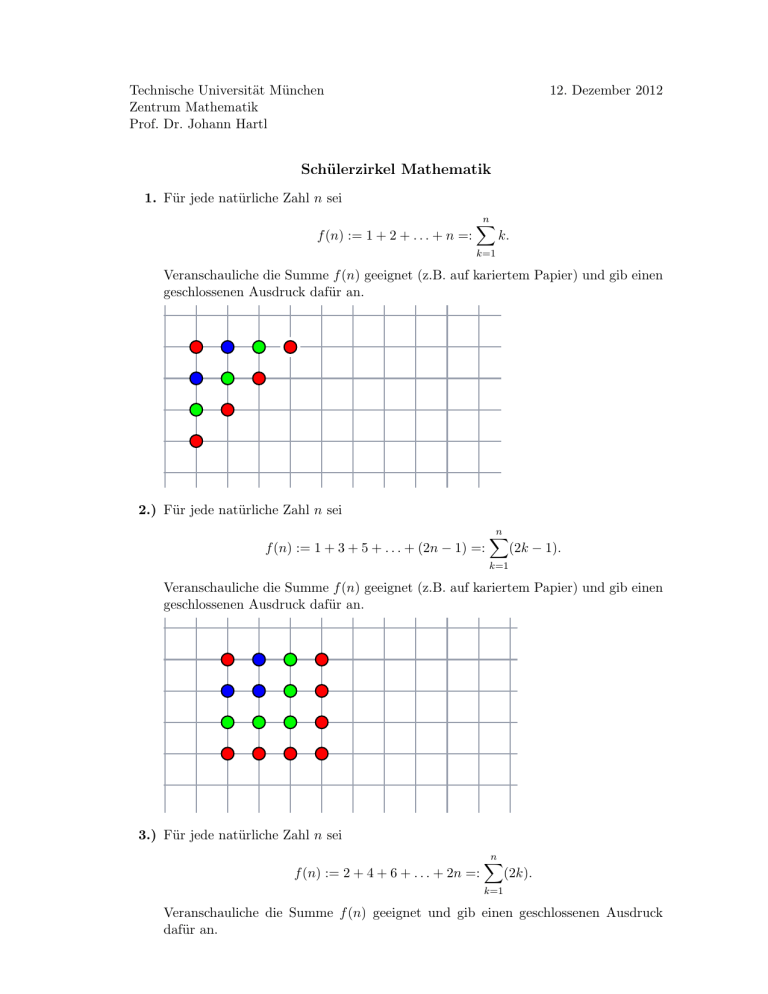
Technische Universität München
Zentrum Mathematik
Prof. Dr. Johann Hartl
12. Dezember 2012
Schülerzirkel Mathematik
1. Für jede natürliche Zahl n sei
f (n) := 1 + 2 + . . . + n =:
n
X
k.
k=1
Veranschauliche die Summe f (n) geeignet (z.B. auf kariertem Papier) und gib einen
geschlossenen Ausdruck dafür an.
2.) Für jede natürliche Zahl n sei
f (n) := 1 + 3 + 5 + . . . + (2n − 1) =:
n
X
(2k − 1).
k=1
Veranschauliche die Summe f (n) geeignet (z.B. auf kariertem Papier) und gib einen
geschlossenen Ausdruck dafür an.
3.) Für jede natürliche Zahl n sei
f (n) := 2 + 4 + 6 + . . . + 2n =:
n
X
(2k).
k=1
Veranschauliche die Summe f (n) geeignet und gib einen geschlossenen Ausdruck
dafür an.
4. Für jede natürliche Zahl n sei
f (n) := 1 + 7 + 19 + . . . + (3n2 − 3n + 1) =:
n
X
(3k 2 − 3k + 1) =
k=1
n
X
(3k(k − 1) + 1).
k=1
Veranschauliche die Summe f (n) geeignet (z.B. mit Würfeln oder vor dem geistigen
Auge) und gib einen geschlossenen Ausdruck dafür an.
5. Für jede natürliche Zahl n sei
f (n) := 1 + 4 + 9 + 16 + . . . + n2 =:
n
X
k2 .
k=1
Veranschauliche die Summe f (n) geeignet (z.B. mit Kugeln oder mit Würfeln oder
vor dem geistigen Auge) und gib einen geschlossenen Ausdruck dafür an.
Warum ist es hier nicht so leicht, einen geschlossenen Ausdruck anzugeben?
Wenn man einen geschlossenen Ausdruck gefunden hat, wie sieht man dann ein, dass
er f (n) für alle natürlichen Zahlen n richtig wiedergibt?
6. Für jede natürliche Zahl n sei
n
f (n) := 1 + 3 + 6 + 10 + . . . +
X k(k + 1)
n(n + 1)
=:
.
2
2
k=1
Veranschauliche die Summe f (n) geeignet (z.B. mit Kugeln oder mit Würfeln oder
vor dem geistigen Auge) und gib einen geschlossenen Ausdruck dafür an.