Fibonacci

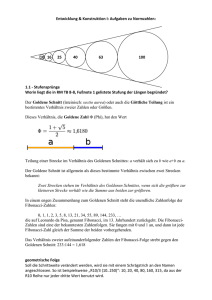
Mathematik für Architekten
Winter 04/05
Fibonacci-Folge – Phyllotaxis – Goldener Schnitt
Pflanzliche Organe bilden Muster. Dies ist besonders schön zu erkennen beim Blattstand von
Laubbäumen, bei Fichten- und Föhrenzapfen, bei gewissen Arten von Kakteen, bei
Blütenböden von Körbchenblütlern (Sonnenblume, Margerite, Silberdistel), bei Maiskolben
und bei den Früchten der Ananas, um nur die Bekanntesten zu nennen. In jedem Fall wird das
Muster gebildet von Elementen (Blüten oder Blätter), die auf zwei verschiedene Arten in
Zeilen oder spiraligen Linien angeordnet sind. Diese Linien bilden zwei Parallelenscharen.
Man unterscheidet Orthostichen (die zwei Scharen verlaufen parallel bzw. senkrecht zur
Wachstumsrichtung) bzw. Parastichen (die Parallelscharen verlaufen schräg: die einen etwas
steiler als die anderen).
Wir werden uns im Folgenden nur mit dem Fall der Parastichen befassen. Wird nun die
Anzahl dieser Parastichen bestimmt, so ergeben sich fast immer zwei ganze Zahlen, deren
Verhältnis zwischen 3/5 und 2/3 liegt. Genauer ergeben sich in den allermeisten Fällen
aufeinander folgende Zahlen der sog. Fibonacci-Folge. Der Anfang dieser Folge wird
gebildet durch die Zahlen
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …
Sie kennen die Tests, bei denen solche Folgenanfänge bekannt sind und der Getestete jetzt die
nächste Zahl hinschreiben muss. Erkennen Sie bei unserer Folge eine Gesetzmässigkeit? Ja,
gewiss – die folgenden Glieder sind 89, 144, 233, 377, 610,… In Worten: Man erhält das
nächstfolgende Glied stets, indem man die beiden Vorgängerglieder addiert. Ist nun die
betreffende Zahlenfolge dadurch eindeutig festgelegt? Nein! Denn auch die Folge
1, 3, 4, 7, 11, 18, 29, 47, 76, …
erfüllt dieselbe Gesetzmässigkeit. Offenbar kommt es zusätzlich auf die beiden
Anfangsglieder an. Die Fibonacci-Folge beginnt mit einer doppelten Eins, während die
soeben erwähnte Folge, die in der mathematischen Literatur Lucas-Folge heisst, mit 1 und 3
beginnt. Kennt man aber die beiden Startglieder und die angegebene Gesetzmässigkeit, so ist
die Folge eindeutig festgelegt.
Leben und Werk des Leonardo von Pisa
Die Fibonacci-Folge erscheint unseres Wissens zum ersten Mal in einem Buch des
Mathematikers und Kaufmanns Leonardo von Pisa. Er wurde um 1175 in Pisa geboren und
starb daselbst nach 1240. „Fibonacci“ ist eine Kurzform für „Filius Bonacci“ (Sohn des
Bonacci). Leonardos Vater Guilielmus Bonacci war Handelsgesandter der Stadt Pisa in der
nordafrikanischen Küstenstadt Bugia (in der Nähe des heutigen Algier gelegen). Leonardo
begleitete seinen Vater und eignete sich dadurch erste Mathematikkenntnisse an. Im Verlauf
zahlreicher Reisen durch den Mittelmeerraum vertiefte er seine Kenntnisse. Er erkannte die
Überlegenheit der indisch-arabischen Rechenmethoden über das herkömmliche Rechnen mit
dem Abakus (Zählrahmen) und war massgeblich beteiligt an der Einführung des indischen
Seite 1
Stellenwertsystems in Europa. Zurück in Pisa schrieb er 1202 den „Liber Abbaci“ (Buch des
Rechenmeisters), mit dem er grosse Berühmtheit erlangen sollte.1
Leonardo lebte in einer Zeit der wirtschaftlichen Blüte; die italienischen Stadtstaaten
prosperierten, allen voran Pisa und Genua. Es war auch eine Zeit des geistigen Aufbruchs,
eine Art Vor-Renaissance. Es ist die Zeit der Scholastik und der ersten europäischen
Universitätsgründungen. Leonardo hatte Kontakt mit dem Hof Friedrichs II. von
Hohenstaufen, Kaiser des Heiligen Römischen Reichs Deutscher Nation, welcher
Wissenschaften und Künste in hohem Masse förderte. Leonardo widmete Friedrich sein
zweites bedeutendes Werk, den „Liber quadratorum“ (1225), ein Buch über den damaligen
Stand der Zahlentheorie. Über Leonardo Fibonacci, seine Zeit und insbesondere über seinen
Liber Abbaci gab es im Herbst 2003 an der ETH Zürich eine sehr aufschlussreiche
Ausstellung. Diese Ausstellung ist in virtueller Form erhalten geblieben. Man findet sie unter
der Internet-Adresse http://www.math.ethz.ch/fibonacci/VirtuellerBesuch (6.10.2004).
Die Kaninchen-Aufgabe
Im Liber Abbaci findet sich u.a. die
berühmt gewordene Kaninchen-Aufgabe.
Die deutsche Übersetzung des lateinischen
Originaltextes lautet:
„Wie viele Kaninchenpaare stammen in
einem Jahr von einem einzigen Paar ab?
Jemand schloss ein Kaninchenpaar in
einen vollständig mit Wänden
abgeschlossenen Raum, um
herauszufinden, wie viele Kaninchenpaare
in einem Jahr von diesem einen Paar
abstammen. Von Natur aus zeugt jedes
Kaninchenpaar ein weiteres Paar pro
Monat. Dieses wiederum beginnt vom
zweiten Lebensmonat an, sich
fortzupflanzen.“
Es geht also um ein Modell, welches die Fortpflanzung von Kaninchen beschreibt. Wie jedes
Modell beschreibt es die Realität, stimmt aber nicht mit ihr überein. Es werden
vereinfachende Annahmen getroffen. Z.B. wird es wohl kaum so sein, dass jedes reale
Kaninchenpaar jeden Monat genau ein neues Paar zeugt. Zudem wird – unausgesprochen –
angenommen, dass im Lauf des Jahres keine Kaninchen sterben.
Nehmen wir einmal an, dass es im Oktober eine bestimmte Anzahl Kaninchenpaare gebe,
beispielsweise 23, und dass es im September 14 waren. Von den Paaren im Oktober sind also
9 neu geboren worden und daher noch nicht zeugungsfähig. Also wird es im November die 23
1
Man muss sich dabei vergegenwärtigen, dass damals der Buchdruck noch nicht erfunden war. Der Erfinder
Johannes Gutenberg lebte erst im 15. Jahrhundert. Es existierte also zunächst nur ein Exemplar eines solchen
Buches. Wenn der Autor Glück hatte, so gab es irgendeinen Sponsor, meist ein Adliger, der bereit war, die
Herstellung einer Abschrift zu finanzieren. Dies war beim Liber Abbaci der Fall. Auf Empfehlung seines
Hofgelehrten Michael Scotus liess Kaiser Friedrich II. höchst persönlich das Buch abschreiben. Diese
„zweite Auflage“ aus dem Jahr 1228 ist uns zusammen mit einigen späteren Abschriften erhalten geblieben,
während das Original von 1202 verschollen ist. Gedruckt wurde der Liber Abbaci jedoch erstmals im 19. Jh.!
Seite 2
Paare vom Oktober, vermehrt um die 14 Paare geben, die von den Kaninchen gezeugt
wurden, die schon im September lebten. Diese Überlegung lässt sich mit beliebigen
Ausgangszahlen durchführen. Wie Leonardo selbst beobachtet hatte, muss man also stets die
Summe bilden, um zur nächsten Zahl zu gelangen:
„…der ersten und der zweiten Zahl, also 1 und 1; dann der zweiten und der dritten, der
dritten und der vierten, der vierten und der fünften, und so weiter, bis zur Summe der zehnten
und der elften Zahl, also 89 und 144, um die Schlusssumme von 233 Kaninchenpaaren zu
finden. In dieser Weise kann für beliebig viele weitere Monate fortgefahren werden.“
An dieser Stelle erscheint also die Folge, die später nach Fibonacci benannt wurde – wohl
zum ersten Mal in Europa. Bezeichnen wir mit fn das Folgenglied mit der Nummer n, so gilt
offenbar die Formel
fn 1  fn  fn 1
und zwar für alle natürlichen (d.h. positiven ganzen) Zahlen n mit n  2 . Dies ist die eingangs
erwähnte Gesetzmässigkeit. Zur vollständigen Bestimmung der Fibonacci-Folge ergänzen wir
f1  f2  1 . Damit ist diese Folge eindeutig festgelegt. Die angegebene Definition ist rekursiv;
sie gestattet sofort, einige weitere Folgenglieder zu berechnen. Die Lucas-Folge, deren n-tes
Glied wir mit l n bezeichnen wollen, genügt der gleichen Rekursions-Formel
ln 1  ln  ln 1
aber die Anfagswerte sind diesmal l1  1 und l2  3 .
Phyllotaxis
Aus den mannigfachen Beispielen zur Phyllotaxis wählen wir den Tannzapfen, also
sozusagen die „Frucht“ der Rottanne oder Fichte. Er besitzt ein sehr eindrückliches
Schuppenmuster. Man erkennt gut, dass dieses Muster zwei Familien von Parastichen enthält.
Diese Parastichen verlaufen spiralig oder – korrekter gesagt – sie bilden Helices
(Schraubenlinien). Dabei kann man sich den Schuppenmantel des idealen Tannzapfens (den
es nicht gibt) als Mantel eines Kreiszylinders denken. Schneidet man diesen Zylindermantel
in Achsenrichtung von oben
bis unten durch, so lässt er
sich abwickeln; d.h. man kann
ihn glätten bzw. in eine Ebene
legen. Auf diese Weise wird
er zum Rechteck, und die
Parastichen werden zu zwei
Parallelenscharen. Dabei sind
die einen etwas steiler als die
anderen. Diese Eigenschaft
bedeutet, dass der Tannzapfen
eine Orientierung oder – wie
man in der Botanik auch sagt
– eine Händigkeit besitzt.
Nennen wir ihn rechtshändig,
falls die steileren Parastichen
von links unten nach rechts
oben verlaufen, andernfalls
Seite 3
linkshändig.
Falls wir mehrere Tannzapfen vor uns haben, ist es wahrscheinlich, dass es darunter sowohl
rechts- als auch linkshändige gibt. Bei genauerem Hinschauen erkennt man auf dem
Tannzapfen-Foto, dass sogar an derselben Fichte sowohl rechts- als auch linkshändige Zapfen
vorkommen können. Diese Entdeckung lässt einen höchst interessanten Schluss zu: Wäre das
Tannzapfenmuster vererbt, so müssten alle Zapfen eines Baums dasselbe Muster haben und
somit auch dieselbe Händigkeit. Also ist das Tannzapfenmuster nicht vererbt sondern bildet
sich bei jedem Zapfen spontan von Neuem! Es ist ein Phänomen der Selbstorganisation.
Wir wollen jetzt die Schuppen unseres Tannzapfens mit Nummern versehen. Wir halten den
Tannzapfen mit der Spitze nach oben, wählen irgendeine Schuppe im untersten Viertel und
markieren sie mit der Zahl 0. Als nächstes müssen wir die Anzahl der Parastichen bestimmen.
Dazu benötigen wir eine Zählstrategie. Sie werden diese sicher selbst herausfinden und dabei
benützen, dass Sie mit der 0-Schuppe einen Startpunkt haben, zu dem Sie immer wieder
zurückkehren können. Wir nehmen an, dass es 5 flachere und 8 steilere Parastichen hat. (Es
stellt sich heraus, dass dies das weitaus häufigste Tannzapfenmuster ist. Sollten Sie andere
Zahlen gefunden haben, so zählen Sie besser noch einmal nach!) Nun versehen wir die flache
durch die 0-Schuppe laufende Parastiche mit der Fünferreihe. Die Schuppen werden also
nacheinander mit den Zahlen 0, 5, 10, 15, 20, 25,… nummeriert. Entsprechend werden die
Schuppen der steileren durch 0 laufenden Parastiche fortlaufend mit den Zahlen der
Achterreihe versehen. Ein erstes kleines Erfolgserlebnis: Die beiden Parastichen treffen sich
ein erstes Mal in der Schuppe mit der Nummer 40 und dann wieder bei 80 und bei 120 (falls
Ihr Zapfen überhaupt so viele Schuppen besitzt). Als Nächstes nummerieren wir auf der
steileren Parastiche durch die 5-Schuppe fortlaufend: 5, 13, 21, 29,… ; die nächste Zahl ist
stets um 8 grösser als die vorangehende. Und auf der steileren Parastiche durch 10 ergibt sich
die Folge 10, 18, 26, 34,… . Auf diese Weise können immer mehr Schuppen mit Nummern
versehen werden. Ferner beachte man, dass auch rückwärts nummeriert werden kann: Auf der
flacheren Parastiche durch 8 ergibt sich 3, durch 16 ergeben sich 11, 6 und 1, durch 24 sind es
19, 14, 9 und 4, und durch 32 schliesslich auch 12, 7 und 2. Was dabei entsteht, kann man als
mathematischen Kristall ansprechen. Dies ist für sich schon eine erstaunliche Tatsache.
Nun hat aber diese Nummerierung einen weiteren Sinn, der über die Schönheit des
Zahlenmusters hinausgeht. Wir beginnen einmal bei der 0-Schuppe, drehen, bis wir die Nr. 1
sehen, drehen weiter zur Nr. 2, dann zur Nr. 3 usw. Durch diese Schuppen lässt sich offenbar
wieder eine Helix legen. Vielleicht steigt sie nicht so regelmässig an wie die gut sichtbaren
Parastichen. Aber insgesamt muss sie doch steigen, denn sie geht durch jede Schuppe
hindurch und die Schuppen mit den grossen Nummern sind definitiv weiter oben als
diejenigen mit den kleinen. Wir nennen sie die erzeugende oder generische Helix des
Musters. Wenn wir den Zapfen von unten anschauen und so von der Schuppe mit der
Nummer n zu derjenigen mit der Nummer n 1 drehen, so scheint es doch, dass wir immer
etwa um den gleichen Winkel drehen müssen. Dies stimmt wohl bei den in der Natur
vorkommenden Zapfen nur näherungsweise, aber beim idealen Zapfen ist das sicher richtig.
Der Winkel einer solchen Drehung heisst in der Fachsprache Divergenzwinkel; wir wollen
ihn mit  bezeichnen und stets im Gradmass (Einteilung des Vollwinkels in 360°) messen.
Doch wie gross ist  ? Eine ganz grobe Abschätzung zeigt, dass der Divergenzwinkel sicher
zwischen 90° und 180° liegt. Doch wir können diese Abschätzung wesentlich verbessern!
Folgen wir nämlich der erzeugenden Helix, dann sehen wir, dass bei der Nummer 2 der volle
Winkel noch nicht erreicht, bei 3 aber schon überschritten ist. Das heisst doch nichts anderes,
als dass
Seite 4
2  360  3
oder anders ausgedrückt:
120    180
Damit haben wir noch nicht viel gewonnen. Aber wir können so weiterfahren: Bei der
Nummer 5 ist der zweite Umlauf noch nicht ganz vollendet, während die 8 nach wenig mehr
als 3 Umläufen erscheint. Also
5  2  360 und 8  3 360
Wir erhalten damit die nächstbessere Eingabelung
135    144 .
Diese Eingrenzung ist natürlich schon viel besser. Doch noch viel lieber möchten wir bei
diesen Eingabelungen eine Gesetmässigkeit erkennen. Zu diesem Zweck schreiben wir die
vorkommenden Winkelgrössen als Vielfache des vollen Winkels
180  12  360, 120  13  360, 144  25  360, 135  83  360
und der Grösse nach geordnet
1
3  360

3
8  360
 
2
5  360

1
2  360
Schauen wir Zähler und Nenner der Faktoren an: Das sind doch alles Fibonacci-Zahlen! Und
bei ihrem Auftreten sind sie der Grösse nach bzw. nach ihrer Nummer in der Folge geordnet.
Dabei ist der Nenner stets grösser als der Zähler. Ersterer ist aber nicht der unmittelbare
Nachbar in der Folge sondern gerade das übernächste Glied. In der Schreibweise des
vorangehenden Abschnittes kann somit jeder Faktor als Bruch der Form
fn
fn  2
dargestellt werden. Wenn man dieses Gedankenspiel weiterverfolgt, so erhält man die
folgende verfeinerte Einschachtelung (wobei jetzt jedes Mal durch 360° dividiert wurde):
1
3

3
8

8
21

21
55
  360 
13
34

5
13

2
5

1
2
3
21
Die Differenz 13
34  55 ist übrigens bereits kleiner als 10 , und es besteht die berechtigte
Hoffnung, dass diese Folge von Einschachtelungen eine einzige reelle Zahl übrig lässt.
Anders ausgedrückt, hat die Folge der Brüche fn fn  2 einen Grenzwert. Wir analysieren
unsere Situation wie folgt: Zunächst gilt offensichtlich:
fn
fn  2

fn  fn 1
f
f
 n  n 1 .
fn  2  fn 1
fn 1 fn  2
Mit dem Bildungsgesetz der Fibonacci-Folge schliessen wir weiter, dass
fn
fn 1

fn 1
f
fn 1
f
1
f
1
 n 
 n 
 n 
fn  2
fn 1 fn  fn 1
fn 1  fn  fn 1 
fn 1  fn

 f

 f  1
n 1
n 1
Wenn wir die Zwischenresultate weglassen, so ergibt sich die Gleichung
Seite 5
fn
fn 1

fn 1
f
1
 n 
fn  2
fn 1  fn


1
 f

n 1
(
Nehmen wir für den Moment an, dass nicht nur die Folge der Brüche
Folge der
fn
fn 1
fn
fn  2
sondern auch die
gegen einen Grenzwert strebt. (Die letztere Folge beginnt mit den Brüchen
1 1 2 3 5
1 , 2 , 3 , 5 , 8 , .)
Bezeichnen wir den Grenzwert von
fn
einmal mit x. Wenn dieser
fn 1
Grenzwert tatsächlich existiert, dann streben doch in der Gleichung, die mit
(
x, und die rechte Seite
strebt gegen
x
1
.
x 1
Da aber für jeden noch so grossen Index n die linke und die rechte Seite von (
übereinstimmen, muss dies auch im Grenzfall gelten. Somit erhalten wir die Gleichung
x2  x 
1
x 1
Diese Gleichung lässt sich nun leicht nach x auflösen. Wir wissen, dass der Grenzwert
zwischen 1/3 und 1/2 liegt, also sicher von Null verschieden ist. Somit dürfen wir beide
Seiten durch x dividieren, und es bleibt
x 
1
x 1
Multiplizieren wir beide Seiten mit x  1 , so ergibt sich die quadratische Gleichung
x  (x  1)  1
Wir erreichen die Standardform dieser Gleichung, indem wir die linke Seite ausmultiplizieren
und auf beiden Seiten 1 subtrahieren:
x2  x  1  0
(2)
Irgendwann haben Sie vermutlich auch schon quadratische Gleichungen gelöst. Erinnern Sie
sich noch daran? Eine solche Gleichung kann stets in die Form
ax 2  bx  c  0
gebracht werden, wobei angenommen wird, dass der Leitkoeffizient a verschieden ist von
Null. (Sonst wäre es ja gar keine quadratische Gleichung.) Falls nun der Ausdruck
D  b 2  4ac positiv ist, so hat die Gleichung die Lösungen
x1 
b 
b 2  4ac
2a
und
x2 
b 
b 2  4ac
.
2a
(Diese Lösungsformeln gelten auch, wenn D  0 ist; die beiden Lösungen stimmen in diesem
Fall überein.) In unserem Beispiel sind
a  1, b  1, c  1 .
Seite 6
Man rechnet leicht nach, dass die Gleichung (2) die folgenden Lösungen besitzt:
1  5
2
x1 
und
x2 
1  5
2
Nun ist aber die für unser Problem relevante Lösung sicher positiv, also scheidet die
algebraisch korrekte Lösung x2 aus. Die gesuchte Lösung ist somit
1  5

2
x1 
5 1
,
2
oder – als Dezimalbruch ausgedrückt –
5 1
 0,618033988
2
x1 
Wie die Zahl 2 ist auch unsere Lösung x1 eine irrationale Zahl; d.h. sie lässt sich nicht als
Bruch von zwei ganzen Zahlen darstellen. Ihre Dezimalbruchentwicklung ist deshalb weder
abbrechend noch periodisch. Nun müssen wir allerdings feststellen, dass wir erst den
Grenzwert der Folge der fn fn1 und nicht etwa den gesuchten der Folge fn fn  2 berechnet
haben. Doch nach unserer Überlegung ist klar, dass die gesuchte Zahl das Quadrat von x1 ist.
Es gilt also
lim
n
2
fn
 x
2
1
fn 2
 5  1
5  2 5 1 3 5




4
2
 2 
wobei lim fn fn2 den Grenzwert (lat.: Limes) der betreffenden Folge bezeichnet. Wir
n
beachten, dass
x12  x1 
5 1 3 5

1
2
2
ist. Somit haben wir
lim
n
fn
fn 2
 1  0, 618033988  0, 381966011
Wir kehren zurück zum Schuppenmuster unseres Tannzapfens. Auf eine ganz bestimmte Art
haben wir diese Schuppen nummeriert. In Gedanken haben wir dann die Schuppen mit
aufeinander folgenden Nummern verbunden. Setzt man diese Verbindungen zusammen, so
entsteht eine einzige Verbindungslinie, die sämtliche Schuppen trifft. Diese Linie kann –
zumindest bei dem uns vorschwebenden idealen Tannzapfen – als Helix (Schraubenlinie)
aufgefasst werden; man nennt sie die erzeugende Helix des Musters. Wenn das tatsächlich
eine Helix ist, dann müssen alle Winkel, um die man den Tannzapfen drehen muss, um von
einer Schuppe zu derjenigen Schuppe mit der nächstgrösseren Nummer zu gelangen, gleich
gross sein. Dieser gemeinsame Winkel  heisst Divergenzwinkel. Wir sind davon
ausgegangen, dass das Muster 5 flachere und 8 steilere Parastichen aufweist. Falls das Muster
die hohe Regelmässigkeit besitzt, die wir in unsere Überlegung hineingesteckt haben, dann
gibt es einen idealen Divergenzwinkelund dieser beträgt

f 
  360   lim n   360  0, 381966  137.50776 .
 n fn 2 
Seite 7
Wenn man nun umgekehrt auf einem Zylindermantel fortlaufend Punkte anbringt, indem man
von Punkt zu Punkt den Zylinder um seine Achse stets um den Winkel   137.5 dreht und
die Höhe (in Achsenrichtung) stets um dasselbe Inkrement vergrössert, so entsteht genau das
ideale Fibonacci-Muster mit den 5 flacheren und 8 steileren Parastichen.
Der Goldene Schnitt
Wir machen hier einen Abstecher in die Proportionenlehre. Von alters her übt die Proportion
des Goldenen Schnittes auf den Menschen eine grosse Anziehungskraft aus. In Architektur
und Kunst wurde und wird sie häufig verwendet – sei dies beabsichtigt oder nicht. Der
goldene Schnitt (früher auch „göttliche Proportion“ genannt) ist ein Begriff aus der
Geometrie. Wir gehen aus von einer Strecke mit den Endpunkten A und B und mit einem
Punkt T, der diese in zwei Teilstrecken oder Abschnitte zerlegt.
M
m
A
T
B
Die Länge des grösseren Abschnitts AT wird mit M (für Major) und diejenige von TB mit m
(für Minor) bezeichnet (s. Figur). Man sagt nun, der Punkt T teile die Strecke AB im
Goldenen Schnitt, falls sich die ganze Strecke zum grösseren Abschnitt gleich verhält wie
der grössere Abschnitt zum kleineren. Formal geschrieben:
(M  m) : M  M : m
(*)
oder – gleichwertig –
M
M m
1

 1
m
M
M
 
m
Setzen wir nun x  M m , so ergibt sich die Gleichung
x  1
1
x
Multipliziert man diese mit der Variablen x und subtrahiert man anschliessend auf beiden
Seiten x  1 , so erhält man die quadratische Gleichung
x2  x  1  0 .
Dass diese Gleichung sehr ähnlich aussieht wie die Gleichung (2) des letzten Abschnitts, ist
– wie sich herausstellen wird – kein Zufall! Wir wenden wieder die weiter oben angegebene
Lösungsformel an – diesmal für
a  1, b  1, c  1
– und erhalten
x1 
1
5
2
und
x2 
1
5
2
Wieder ist x2 negativ und kommt als Verhältnis zweier Streckenlängen nicht in Frage. Die
einzige Lösung ist somit
Seite 8
x1 
1
5
2
 1,618033988
Wir rekapitulieren, dass wir die Bezeichnung x für das Verhältnis von Major zu Minor des
Goldenen Schnittes eingesetzt haben. Es gilt also
M 1 5

 1,618033988
m
2
D.h. die Irrationalzahl 1,618033988… ist der numerische Ausdruck für das Teilverhältnis des
Goldenen Schnittes. Indem wir diese Zahl mit  bezeichnen, schliessen wir uns H.S.M.
Coxeter2 an. Sie haben bestimmt schon bemerkt, dass sich die Zahl  von der im
Zusammenhang mit dem idealen Divergenzwinkel  aufgetretenen Zahl 0,618033988… um
genau 1 unterscheidet. Doch es kommt noch besser: Für ein tieferes Verständnis des goldenen
Schnittes ist es sicher ratsam auch den Minor zum Major ins Verhältnis zu setzen, also den
Kehrwert von  zu bilden. Diese Zahl wird im Folgenden mit  bezeichnet. Bei der Bildung
des Kehrwertes kommt ein Wurzelausdruck in den Nenner. Erweitert man diesen Bruch mit
einem passenden anderen Wurzelausdruck, so wird der Nenner wurzelfrei:

1


m
2


M
1 5
2
5  1 2( 5  1)



5 1
5 1 5 1
5 1
2
Der Term auf der rechten Seite der letzten Gleichung ist uns vom Abschnitt über die
Phyllotaxis wohlbekannt! Dies ist doch gerade der Grenzwert der Folge fn fn1 der
Quotienten aufeinander folgender Glieder der Fibonacci-Folge. Zur Bestimmung des idealen
Divergenzwinkels  benötigten wir nicht diesen Grenzwert sondern sein Quadrat. Dabei
stellte sich heraus, dass sich die beiden Werte gerade zu 1 ergänzen. Dies lässt nun die
folgende geometrische Interpretation zu: Markiert man auf der Zahlengeraden das Intervall
aller reellen Zahlen von 0 bis 1, so teilt die Zahl  dieses Intervall gerade im goldenen Schnitt
mit  als Major und 1     2 als Minor; denn 1 :    :  2 .

1


0
1
2
3
Schauen wir uns noch einmal an, wie wir den Divergenzwinkel  berechnet haben:

f 
  360   lim n   360   2  137.50776
 n fn 2 
Also ist der Divergenzwinkel  nichts anderes als der Minor, wenn man den Vollwinkel – hier
als Intervall dargestellt – im Goldenen Schnitt teilt!
0°
2
 = 137.5°
360°
H.S.M. Coxeter (1907–2003), englischer Mathematiker. Sein Buch „Unvergänglivhe Geometrie“
(Birkhäuser, Basel/Stuttgart 1963) enthält ein Kapitel über den Goldenen Schnitt und die Phyllotaxis.
Seite 9
Es wird vermutet, dass der Goldene Schnitt von den Pythagoreern entdeckt wurde. Dies war
ein von Pythagoras3 gegründeter Geheimbund, der sich mit Mathematik und Musiktheorie
befasste – im Spannungsfeld zwischen Wissenschaft und Esoterik. Dieser Geheimbund
verwendete als Erkennungszeichen das Pentagramm, d.h. das Diagonalengebilde des
regulären Fünfecks. (Ein Fünfeck ist regulär, wenn nicht nur alle fünf Seiten gleich lang
sondern auch alle fünf Innenwinkel gleich gross sind.
Wir behaupten nun, dass in einem regulären Fünfeck jeder Schnittpunkt von zwei Diagonalen,
welche keine gemeinsame Ecke besitzen, beide Diagonalen im Verhältnis des Goldenen
Schnittes teilt.
C
B
A
F
D
E
Da jede Diagonale parallel ist zur gegenüber liegenden Fünfecksseite, erkennt man, dass der
grössere Diagonalenabschnitt gleich lang ist wie die Fünfecksseite. Also ist die Behauptung
mit der Gültigkeit der Proportion () gleichwertig:
d : s  s : (d  s)
().
Dabei bedeuten s die Länge einer Fünfecksseite und d die Diagonalenlänge. Für einen Beweis
dieser Tatsache überlegt man sich, dass die beiden gleichschenkligen Dreiecke ABC und DEF
ähnlich sind, d.h. sie haben die gleiche „Form“ oder – präziser ausgedrückt – entsprechende
Winkel stimmen überein. In der Tat ist die letztere Eigenschaft erfüllt, denn je zwei
entsprechende Dreiecksseiten sind parallel; z.B. gilt dies für die Seiten BC und EF. Nun weiss
man aber aus der elementaren Geometrie, dass in ähnlichen Dreiecken die Verhältnisse
entsprechender Seiten gleich sind. Insbesondere verhält sich die Basis AB des grösseren
Dreiecks zu seinem Schenkel AC gleich wie die Basis DE des kleineren zu dessen Schenkel
DF. Verwenden wir jetzt die eingeführten Abkürzungen d und s, so erhalten wir genau die
Gleichung (). Also verhalten sich Diagonale und Seite im regulären Fünfeck wie Major und
Minor des goldenen Schnittes. Anders ausgedrückt, teilt beispielsweise der Punkt F die
beiden Diagonalen AE und BD je im Goldenen Schnitt. Folglich gilt
d
  , bzw. d  s    s 1, 618033988
s
und
3
Pythagoras von Samos (ca. 590–510 v.Chr.), griechischer Philosoph, Mathematiker und Begründer der
Harmonielehre
Seite 10
s
 , bzw. s  d    d  0, 618033988
d
Wir werden ein gleichschenkliges Dreieck ein goldenes Dreieck nennen, wenn zwischen
Basis und Schenkellänge das Verhältnis des Goldenen Schnittes besteht. Bei einem
stumpfwinkligen goldenen Dreieck verhält sich die Basis zum Schenkel wie  :1 . Ein
spitzwinkliges goldenes Dreieck ist hingegen dadurch charakterisiert, dass sich die Basis zum
Schenkel wie  :1 verhält. Die Pentagramm-Figur (mit ergänzendem Fünfeck) enthält
mehrere spitzwinklige und stumpfwinklige goldene Dreiecke. Beispielsweise sind die
Dreiecke DEC und ABC golden; Dreieck DEC ist spitzwinklig, ABC hingegen stumpfwinklig.
Ein Zitat
Für das Verständnis des nachfolgenden Kepler-Zitats ist es wichtig zu wissen, dass der
Zitierte – wie die Griechen zur Zeit von Pythagoras – mit „Zahlen“ stets ganze Zahlen meint.
Irrationale Verhältnisse wie  oder  können demnach nicht als Verhältnisse von Zahlen
ausgedrückt werden; sie galten deshalb als „unaussprechbar“. Der Goldene Schnitt heisst bei
Kepler „Göttlicher Schnitt“ oder „Teilung nach dem äusseren und mittleren Verhältnis“. (Die
letztere Bezeichnungsweise geht auf Euklid4 zurück; der Ausdruck „Goldener Schnitt“ ist
wesentlich jüngeren Datums.)
„Zunächst erinnere man sich …, dass das Fünfeck durch die Teilung nach dem äusseren
und mittleren Verhältnis bestimmt ist, die den göttlichen Schnitt bildet. In diesem schönen
Verhältnis liegt nun aber die Idee der Zeugung verborgen. Denn wie der Vater den Sohn
erzeugt, der Sohn einen anderen, jeder einen ihm ähnlichen, so wird auch bei jener Teilung
die Proportion fortgesetzt, wenn man den grösseren Abschnitt zum Ganzen hinzufügt. Die
Summe erhält dann die Stelle des Ganzen, und was vorher Ganzes war, ist jetzt grösserer
Abschnitt.“
Hier wird die Tatsache angesprochen, dass der goldene Schnitt auch besteht zwischen der um
den Major verlängerten ganzen Strecke und letzterer, und dass sich diese Eigenschaft immer
weiter fortpflanzt. Analog teilt der Minor den Major im goldenen Schnitt, wird dabei selbst
zum Major, der nun von seinem Minor wieder im goldenen Schnitt geteilt wird, usw. Aus
diesem Grund wird der goldene Schnitt auch etwa „stetige Teilung“ genannt. Drücken wir die
angesprochenen Tatsachen algebraisch aus, so ergeben sich
M : m  (M  m) : M  (2M  m) : (M  m)  (3M  2m) : (2M  m)  
bzw.
M : m  m : (M  m)  (M  m) : (2m  M )  
Kepler fährt weiter:
„Wenn auch dieses Verhältnis nicht durch Zahlen ausgedrückt werden kann, so gibt es
doch eine Zahlenreihe, die dem wahren Wert des Verhältnisses immer näher kommt. In
dieser Reihe erzeugt der Unterschied der Zahlen gegenüber den wirklichen
Proportionsgliedern (die unaussprechbar sind) in höchst merkwürdiger Weise Männchen
und Weibchen, wie sie sich durch ihre Geschlechtsglieder unterscheiden. Es sei zunächst
der grössere Teil 2, der kleinere 1, das Ganze 3. Es verhält sich nun nicht genau 1 zu 2 wie
4
Euklid von Alexandria (ca. 365–300 v.Chr.), griechischer Mathematiker, Verfasser der „Elemente“, einer
Sammlung von Mathematik-Lehrbüchern, die heute noch verwendet werden.
Seite 11
2 zu 3; vielmehr bleibt das Rechteck aus den Aussengliedern 1 und 3 hinter dem Quadrat
des Mittelgliedes um eine Einheit zurück. Addiert man nun 2 und 3, so erhält man als
neues Ganzes 5; addiert man 3 und 5, so erhält man als Ganzes 8 usw. Das Rechteck aus 1
und 3 erzeugt ein Weibchen, denn es fehlt ihm eine Einheit gegenüber dem Quadrat von 2.
Das Rechteck aus 2 und 5 erzeugt ein Männchen, denn es überschreitet das Quadrat von 3
um eine Einheit. Das Rechteck aus 3 und 8 erzeugt ein Weibchen, denn es fehlt ihm eine
Einheit gegenüber dem Quadrat von 5. Aus 5 und 13 entsteht wieder ein Männchen, im
Hinblick auf das Quadrat von 8; aus 8 und 21 ein Weibchen im Hinblick auf das Quadrat
von 13 usw. bis ins Unendliche.
Das ist also die Natur der Teilung, die bei der Herstellung des Fünfecks Verwendung
findet.…“ Dieses Zitat stammt aus Keplers5 Weltharmonik, 3. Buch, S. 165–166. Dieses
bedeutende Werk, welches auch das dritte Keplersche Gesetz über Planetenbahnen
enthält, erschien 1619 in lateinischer Sprache. Die deutsche Fassung besorgte M. Caspar
(München/Berlin 1939).
Die nachstehende Veranschaulichung des Zitats geht auf eine Idee Keplers zurück, die sich
am Rand der entsprechenden Buchseite findet.
1:2  2 : 3
1)
bzw.
1  3  22
genauer
1  3  22  1
2 :3  3:5
2)
bzw.
2  5  32
genauer
2  5  32  1
3:5  5 :8
3)
bzw.
3  8  52
genauer
3  8  52  1
5 : 8  8 :13
4)
bzw.
5 13  8 2
genauer
5 13  8 2  1
Kepler war also vom Goldenen Schnitt ausgegangen und stiess auf die Fibonacci-Folge, weil
er das „unaussprechbare“ Verhältnis durch ganzzahlige Verhältnisse annähern wollte. Er
5
Johannes Kepler (1571–1630), bedeutender deutscher Astronom und Mathematiker der frühen Neuzeit.
Seite 12
wusste also bereits um den Zusammenhang zwischen der Fibonacci-Folge und dem Goldenen
Schnitt, dem wir weiter oben begegnet sind:
lim
n
fn 1
1 5
 
fn
2
Kepler gelangte zu dieser Einsicht, indem er eine Eigenschaft der Fibonacci-Folge entdeckte,
die heute Simson-Identität genannt wird. In formaler Sprache lautet sie:
fn1  fn1  fn 2  (1)n
für alle n (n  2)
Dividiert man beide Seiten durch fn 1  fn , so erhält man die Gleichung
fn1
fn
(1)n


fn
fn1 fn1  fn
Aus dieser Form der Simson-Identität lässt sich nun eine Eingabelung der Zahl  finden,
welche der Eingabelung des Divergenzwinkels (s. Abschnitt über Phyllotaxis) analog ist:
1
3
2

8
5

21
13
 
34
21

13
8

5
3
 2.
Seite 13