Lösung22 (MS Word)

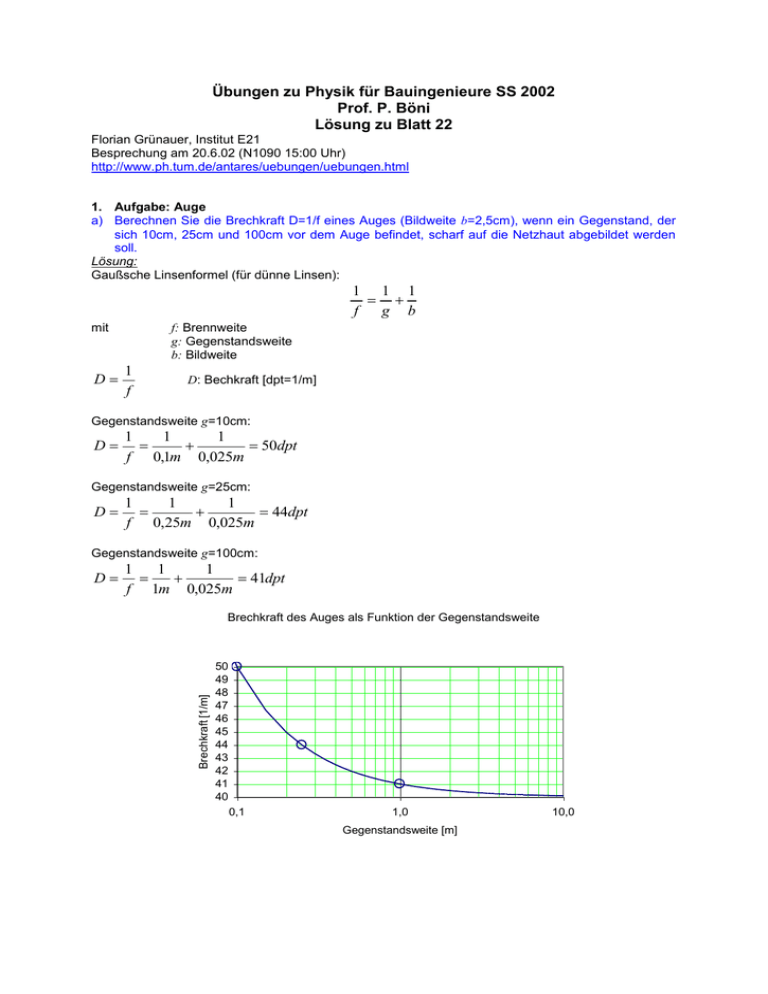
Übungen zu Physik für Bauingenieure SS 2002
Prof. P. Böni
Lösung zu Blatt 22
Florian Grünauer, Institut E21
Besprechung am 20.6.02 (N1090 15:00 Uhr)
http://www.ph.tum.de/antares/uebungen/uebungen.html
1. Aufgabe: Auge
a) Berechnen Sie die Brechkraft D=1/f eines Auges (Bildweite b=2,5cm), wenn ein Gegenstand, der
sich 10cm, 25cm und 100cm vor dem Auge befindet, scharf auf die Netzhaut abgebildet werden
soll.
Lösung:
Gaußsche Linsenformel (für dünne Linsen):
1 1 1
 
f
g b
mit
D
f: Brennweite
g: Gegenstandsweite
b: Bildweite
1
f
D: Bechkraft [dpt=1/m]
Gegenstandsweite g=10cm:
D
1
1
1


 50dpt
f 0,1m 0,025m
Gegenstandsweite g=25cm:
D
1
1
1


 44dpt
f 0,25m 0,025m
Gegenstandsweite g=100cm:
1
1
1


 41dpt
f 1m 0,025m
Brechkraft des Auges als Funktion der Gegenstandsweite
Brechkraft [1/m]
D
50
49
48
47
46
45
44
43
42
41
40
0,1
1,0
Gegenstandsweite [m]
10,0
b) Nehmen Sie nun an, daß der Nahpunkt (=deutliche Sehweite des Auges) 75cm vor dem Auge
liegt. Welche Brechkraft muß eine Lesebrille haben, damit der Nahpunkt auf einen Abstand von
25cm heranrückt?
Lösung:
Kombination zweier dünner Linsen:
1
f ges
1
1
d


f1 f 2 f1 f 2

mit d: Abstand beider Linsen
Annahme: der Abstand beider Linsen soll viel kleiner sein, als die Brennweiten der einzelnen Linsen.
Für d<<f i gilt:
1
1 1
oder
 
f ges f1 f 2
Dges  D1  D2
hier:
Dges  DAuge  DBrille (I)
ohne Brille:
DAuge 
1
g ohneBrille

1
b
(II)
mit Brille:
Dges 
1
g mitBrille

1
b
(III)
(II) und (III) in (I) einsetzen:
1
1
1
1

  DBrille
g mitBrille b g ohneBrille b
1
1
1
1
DBrille 



 2,67m 1
g mitBrille g ohneBrille 0,25m 0,75m

2. Aufgabe: Kamera
Mit einer Kamera mit verstellbarem Objektiv soll ein Adler mit einer Flügelspannweite von 2m
aufgenommen werden. Der Adler sei 30m entfernt.
a) Welche Brennweite ist zu wählen, damit die Flügel die gesamte Breite des Bildes (36mm)
einnehmen?
1. Lösungsweg:
Transversalvergrößerung:

G
B b
Bg
(I)
 b
G g
G
(I) in Gaußsche Linsenformel einsetzen:
1 1 1
1 1 G
1  G
    
 1   (II)
f
g b
f
g Bg g 
B
g


g

f  
 1  (G / B) 
f
hier:
b


30m
30m
 
f  
 53cm
3
 1  (2  10 mm / 36mm)  56,555
B
2. Lösungsweg:
Aus dem Verlauf der Strahlen durch den Brennpunkt und durch den Linsenmittelpunkt folgt direkt:

B
f
B
B B
g


 f  ( g  f )  f 1    g  f 
G
G (g  f )
G
 G G
1
B
Anmerkung: In der Literatur findet man häufig eine andere Vorzeichenkonvention für die gilt:

B b
Die Bildgröße B ist hierbei negativ für ein umgekehrtes Bild.

G
g
b) Wie verändert sich die Belichtungszeit, wenn die Blendenzahl von k=5,6 auf k=8 vergrößert wird?
(Es soll jeweils eine gleich große Lichtmenge auf den Film gelangen).
Allgemein:
D: Blendendurchmesser
f: Brennweite
D/f: Öffnungsverhältnis
f/D: Blendenzahl
häufig verwendeter Ausdruck für die Blendenzahl: f /# 
f
D
f/# ist hierbei wie ein einziges Symbol zu verstehen.
Die Lichtmenge, die durch die Blende gelangt, ist proportional zur Blendenfläche, also zu D2.
Diese Lichtmenge wird auf die ausgeleuchtete Fläche in der Bildebene verteilt.
Aus der
Transversalvergrößerung

B
f
f


G ( g  f ) x0
folgt, daß die ausgeleuchtete Fläche in der Bildebene proportional zu f2 sein muß. Daher ist die
Flußdichte in der Bildebene proportional zum Quadrat des Öffnungsverhältnisses.
 D
 
 f 
2
Gewöhnlich haben Objektivblenden Blendenzahlenmarkierungen von
1, 1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22.
Das größte Öffnungsverhältnis entspricht in diesem Fall 1.
Jede
aufeinanderfolgende
Blendeneinstellung vergrößert f / D durch einen Faktor 2 (innerhalb der numerischen Rundung)
und verkleinert somit die Flußdichte in der Bildebene um den Faktor 1/2. Daher erreicht die gleiche
Lichtmenge den Film, wenn die Kamera für Blendenzahl 1.4 auf 1/500sec, für 2 auf 1/250sec, für 2.8
auf 1/125sec usw. eingestellt ist.
Lösung:
Sei  die Lichtmenge pro Zeit und Fläche in der Bildebene. Dann gilt:
2
 D
1
       mit k: Blendenzahl
k
 f 
2
 1 
 k 8  8 
  31,36  1

 k 5.6  1 
64
2


 5.6 
2
d.h. die Lichtmenge pro Fläche und Zeit hat sich halbiert. Somit muß die Belichtungszeit verdoppelt
werden.
3. Aufgabe: Mikroskop
Ein Mikroskop besteht aus einem Objektiv mit der Brennweite f 1=4mm und einem Okular mit der
Brennweite f2=1cm. Der Abstand x zwischen Objektiv und Okular beträgt 12cm.
a) Welchen Abstand muß der Gegenstand vom Objektiv haben, damit der Beobachter dessen Bild
im Unendlichen liegen sieht?
Damit der Beobachter das Bild im Unendlichen liegen sieht, muß das Objektiv ein reelles Bild in der
Brennebene des Okulars erzeugen. Der Abstand x zwischen Objektiv und Okular beträgt 12cm. Das
Bild des Objektivs muß also in einem Abstand von x-f2=11cm hinter dem Objektiv liegen.
Die Gegenstandsweite ergibt sich aus der Gaußschen Abbildungsgleichung:
1 1 1
1
1
  g

 0,415cm
1 1
1
1
f
g b


f b 0,4cm 11cm
b) Wie stark vergrößert das Mikroskop?
Vergrößerung des Objektivs:
VObjektiv 
bObjektiv
g Objektiv
 1
1  bObjektiv  f Objektiv
t
 bObjektiv 



f

f Objektiv
f Objektiv
 Objektiv bObjektiv 
mit t: Tubuslänge
Vergrößerung des Okulars:
Da das Okluar kein reelles Bild erzeugt, kann nicht mit der transversalen Vergrößerung gerechnet
werden. Das reelle Bild entsteht erst auf der Netzhaut des Beobachters. Die subjektive Empfindung
der Größe eines Gegenstandes wird durch den Gesichtsfeldwinkel (Sehwinkel)  bestimmt, unter dem
der Gegenstand vom Beobachter wahrgenommen wird. Wenn die Gegenstandsweite beliebig
verringert werden kann (z.B. beim Mikroskop), verwendet man als Referenz den Sehwinkel unter dem
das Objekt durch das Auge ohne Instrument im Abstand der konventionellen Sehweite S0=25cm
gesehen wird.
VOkular 
Sehwinkel _ mit _ Instrument  I

Sehwinkel _ bei _ S 0
0

G
S0
VOkular 
S0
 I G / f Okular
25cm



0
G / S0
f Okular
f Okular
 
G
f
Vergrößerung des Mikroskops:
VMikroskop  VObjektiv  VOkular 
hier:
VMikroskop 
t  S0
f Objektiv  f Okular
10,6cm  25cm
 662,5
0,4cm  1cm
4. Aufgabe: Föhn
Warum sind bei Föhn und klarer Sicht die Berge "zum Greifen nahe"?
Warme Luftschichten;
geringere Dichte;
geringerer
Brechnungsindex
Kalte Luftschichten;
höhere Dichte;
höherer Brechnungsindex