MMIKlausur20042E

F A C H H O C H S C H U L E
F Ü R
D I E
W I R T S C H A F T
F H D W ,
H A N N O V E R
M AT H E M AT I S C H E M O D E L L E
P ETRI -N ETZE
ERSATZKLAUSUR
Studiengang: Informatik
Studienquartal: VI. Theoriequartal
Prüfungsumfang: Petri-Netz-Skript vom 2. Juni 2004.
Dozent: Löwe
Termin: 2. August 2004
Dauer: 60 Minuten
20 Punkte sind zu erreichen: Wissen 8, Anwendung 8 und Transfer 4 Punkte. Bestanden ab 10 Punkte.
TEIL I: WISSEN (20 MINUTEN)
Aufgabe 1 (2 Punkte): Warum sind Transitionen in einfachen Petri-Netzen1 in der Regel nicht von sich
selbst parallel unabhängig? Das ist in erweiterten Netzen2 anders! Warum?
Aufgabe 2 (2 Punkte): Was ist ein Schritt in erweiterten Petri-Netzen?
Aufgabe 3 (2 Punkte): Wann ist ein Schritt in erweiterten Petri-Netzen in einem Zustand aktiviert?
Aufgabe 4 (2 Punkte): Wie wird der Zustand verändert, wenn ein aktivierter Schritt in erweiterten Netzen schaltet?
TEIL II: ANWENDUNG ( 20 MINUTEN)
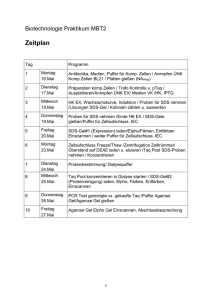
Betrachten Sie das erweiterte Petri-NetzSystem zur Rechten, in dem alle Gewichte
von Elementen der Flussrelation 1 sind.
Das Netzsystem stellt 3 Prozesse, die in
einen Puffer schreiben, und 3 Prozesse, die
aus demselben Puffer lesen, dar. Die Anzahl
der „Token“ in dem Puffer definiert den
Füllstand des Puffers.
Puffer
3
will
schreiben
hat geschrieben
will
lesen
20
3
3
hat gelesen
3
Aufgabe 5 (2 Punkte): Ergänzen Sie in
dem System alle Komplementärstellen!
Aufgabe 6 (3 Punkte): Erweitern Sie das
Netzsystem so, dass nach maximal 2
Schreibvorgängen hintereinander in den Puffer auf jeden Fall ein Lesevorgang aus dem Puffer folgt, auch
wenn der Puffer noch nicht voll ist.
Aufgabe 7 (3 Punkte): Erweitern Sie das Netzsystem um einen Mechanismus, der ab 15 noch nicht
gelesenen Einträgen in dem Puffer (Füllstand  15) einen zusätzlichen Leser erzeugt. Dieser zusätzliche
Leser soll wieder entfernt werden, wenn der Füllstand des Puffers unter 10 (Füllstand  10) sinkt.
1
2
Einfache Petri-Netze haben Kapazität 1 an allen Stellen und Gewicht 1 an allen Flussrelationen.
Erweiterte Petri-Netze haben Kapazitäten  1 an allen Stellen und Gewicht  1 an allen Flussrelationen.
TEIL III: TRANSFER (20 MINUTEN)
Sei ein einfaches Petri-Netz-System N = (N = (S, T, F), z0) gegeben.
(1) Dann ist eine Transition t in N lebendig, wenn für alle erreichbaren Zustände z  R(N) gilt: Es gibt
eine Schaltsequenz z  z1 ... zn  z’ so, dass t in Zustand z’ aktiviert ist.
(2) Das Netzsystem N heißt lebendig, wenn alle seine Transitionen lebendig sind.
(3) Das Netzsystem N heißt zyklisch, wenn es von jedem erreichbaren Zustand in jeden anderen erreichbaren Zustand eine Schaltsequenz gibt, i.e. wenn für je zwei erreichbare Zustände z und z’ eine Sequenz z  z1 ... zn  z’ existiert.
(4) Dann bezeichnet N-1 = (N-1 = (S, T, F-1), z0) das inverse Netz zu N, wobei F-1 = {(y, x)|(x, y)  F}.
Das heißt, dass in N-1 lediglich alle Pfeile umgedreht sind.
Aufgabe 8 (2 Punkte): Ist N-1 zyklisch, wenn N zyklisch ist? Wenn ja, warum? Wenn nein, bitte Gegenbeispiel angeben!
Aufgabe 9 (2 Punkte): Ist N-1 lebendig, wenn N lebendig ist? Wenn ja, warum? Wenn nein, bitte Gegenbeispiel angeben!
2