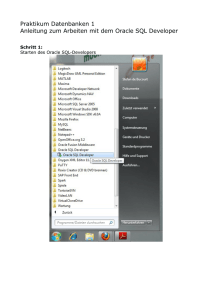
Document

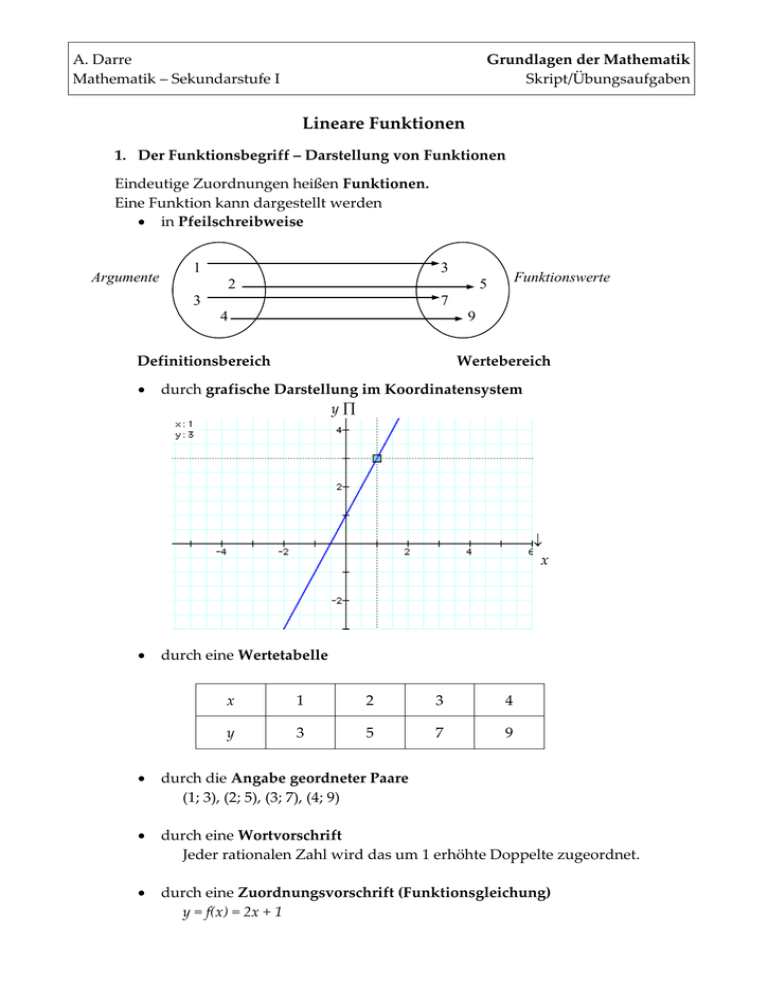
Grundlagen der Mathematik
Skript/Übungsaufgaben
A. Darre
Mathematik – Sekundarstufe I
Lineare Funktionen
1. Der Funktionsbegriff – Darstellung von Funktionen
Eindeutige Zuordnungen heißen Funktionen.
Eine Funktion kann dargestellt werden
 in Pfeilschreibweise
Argumente
1
3
2
3
7
4
9
Definitionsbereich

Funktionswerte
5
Wertebereich
durch grafische Darstellung im Koordinatensystem
y

x

durch eine Wertetabelle
x
1
2
3
4
y
3
5
7
9

durch die Angabe geordneter Paare
(1; 3), (2; 5), (3; 7), (4; 9)

durch eine Wortvorschrift
Jeder rationalen Zahl wird das um 1 erhöhte Doppelte zugeordnet.

durch eine Zuordnungsvorschrift (Funktionsgleichung)
y = f(x) = 2x + 1
A. Darre
Mathematik – Sekundarstufe I
Grundlagen der Mathematik
Skript/Übungsaufgaben
2. Lineare Funktionen – Definitionen
Lineare Funktionen haben die Form
y = f(x) = m x + n
Anstieg der
Geraden
y
m=
x
.
Schnittpunkt
mit der y-Achse
Alle Punkte des Graphen einer linearen Funktion liegen auf einer Geraden.
Jede Zahl x aus dem Definitionsbereich einer Funktion f, für die f(x) = 0 gilt, heißt
Nullstelle dieser Funktion.
Zeichnen des Graphen einer linearen Funktion im Koordinatensystem
Gegeben sind zwei Punkte P und Q:
Verbinden der Punkte ergibt den Graphen der Funktion f (Gerade).
Gegeben ist die Funktionsgleichung y = f(x):
 In der Gleichung y = mx + n bezeichnet n den Schnittpunkt mit der y-Achse.
Ein Punkt der Geraden ist also P(0; n).
 Von P aus geht man eine Einheit nach rechts und dann m Einheiten nach
oben (für m > 0) bzw. |m| Einheiten nach unten (für m < 0). Dort liegt der
zweite Punkt Q(1; n + m)
 Die beiden Punkte P und Q werden durch eine Gerade verbunden.
Monotonie einer linearen Funktion
monoton steigend
m>0
Eine lineare Funktion heißt
, wenn der Anstieg
monoton fallend
m<0
Lineare Funktionen
ist.
Seite 2
A. Darre
Mathematik – Sekundarstufe I
Grundlagen der Mathematik
Skript/Übungsaufgaben
3. Lineare Funktionen – Einführungsbeispiele
3.1 Beispiele
(1) Eine lineare Funktion ist gegeben durch die Bildungsvorschrift
y = f(x) = -0,5x + 1.
Die Funktion ist graphisch darzustellen und die Nullstelle zu berechnen.
Es ist für x   im Intervall –3 ≤ x ≤ 3 eine Wertetabelle zu erstellen.
Das Monotonieverhalten der Funktion ist anzugeben.
Graphische Darstellung
Berechnung der Nullstelle
0 = -0,5x + 1
=
x=
Lösen einer linearen Gleichung durch
Äquivalenzumformungen
Wertetabelle erstellen
Die Funktionswerte sind durch Einsetzen in die Funktionsgleichung zu
berechnen und in der Tabelle abzutragen, z.B. y = f(-3) = -0,5 . (-3) + 1 = 2,5.
x
-3
-2
-1
0
1
2
3
y
Montonieverhalten
Lineare Funktionen
f ist monoton
, da
.
Seite 3
A. Darre
Mathematik – Sekundarstufe I
Grundlagen der Mathematik
Skript/Übungsaufgaben
(2) Es sind die Punkte P(-1; -4,5) und Q(3; 1,5) einer linearen Funktion f
gegeben. Bestimme die Funktionsgleichung der Geraden und stelle diese
graphisch dar. Ermittle die Nullstelle von f und beschreibe das
Monotonieverhalten.
x1 = -1
f(x1) = y1 = -4,5
m=
y
=
x
y2 – y 1
x2 – x1
x2 = 3
f(x2) = y2 = 1,5
=
1,5 – (-4,5)
3 – (-1)
=
6
= 1,5
4
y = mx + n
n = y – mx
(allgemeine Form einer linearen Funktion)
(Umstellen nach n)
Der Anstieg wurde bereits ermittelt. Nun benötigen
wir noch ein x und den zugehörigen y-Wert. Die sind
durch die beiden Punkte P oder Q gegeben. Also
ergeben sich zwei Möglichkeiten der Berechnung:
n = y 1 – m . x1
oder
n = y 2 – m . x2
.
n = (-4,5) – 1,5 (-1)
n = 1,5 – 1,5 . 3
n = -3
n = -3
Demnach ergibt sich für die Funktionsgleichung y = f(x) = 1,5x – 3.
Graphische Darstellung
Nullstelle
Lineare Funktionen
0 = 1,5x – 3
=
x=
Monotonieverhalten
Seite 4
A. Darre
Mathematik – Sekundarstufe I
Grundlagen der Mathematik
Skript/Übungsaufgaben
3.2 Anwendungsbeispiel
Der Telefondienst "Handybillig" (HB) bietet an: Monatliche Grundgebühr 13 €,
jede Gesprächsminute kostet 0,08 €.
Anbieter "Handypreiswert" (HP) wirbt mit 10 € Grundgebühr pro Monat, jede
Gesprächsminute soll 0,10 € kosten.
Bei wie viel Minuten sind die Kosten bei beiden gleich?
Die Gesamtkosten werden durch f(x) bei Anbieter „Handybillig“ und g(x) bei Anbieter
„Handypreiswert“ beschrieben. Also sind die Funktionsgleichungen gleichzusetzen und nach x
umzustellen.
Bei 150 Gesprächsminuten sind bei beiden Anbietern die Kosten gleich
(25 €).
Ihnen stehen 30 € monatlich zum Telefonieren zur Verfügung (Oma zahlt).
Welchen Dienst wählen Sie und wie lange können Sie bei dem gewählten
Anbieter telefonieren?
HB ist der günstigere Anbieter, denn für 30 € kann dort 212,5 Minuten
telefoniert werden.
Stellen Sie den Sachverhalt graphisch dar.
Lineare Funktionen
Seite 5
A. Darre
Mathematik – Sekundarstufe I
Grundlagen der Mathematik
Skript/Übungsaufgaben
4. Übungsaufgaben
Aufgabe 1
Aufgabe 2
Aufgabe 3
Lineare Funktionen
Seite 6
A. Darre
Mathematik – Sekundarstufe I
Grundlagen der Mathematik
Skript/Übungsaufgaben
Aufgabe 4
Aufgabe 5
Aufgabe 6
Lineare Funktionen
Seite 7
A. Darre
Mathematik – Sekundarstufe I
Grundlagen der Mathematik
Skript/Übungsaufgaben
Aufgabe 7
Lineare Funktionen
Seite 8
A. Darre
Mathematik – Sekundarstufe I
Aufgabe 8
Grundlagen der Mathematik
Skript/Übungsaufgaben
A. Darre
Mathematik – Sekundarstufe I
5. Hausaufgaben
Hausaufgabe 1
Hausaufgabe 2
Grundlagen der Mathematik
Skript/Übungsaufgaben