inferenzstatistik

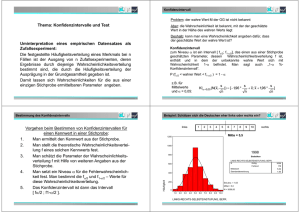
Inferenzstatistik
Vorlesung „Mathematik und Statistik für Raumplaner“
A.o. Universitätsprofessor Dr. W. Blaas
Institut für Finanzwissenschaft und Infrastrukturpolitik
Technische Universität Wien
Version vom 2. Mai 2006
Vorlesung Inferenzstatistik
2
INHALTSVERZEICHNIS
1. Einleitung
2. Auswahl von Stichproben
2.1. Die bewusste Auswahl
2.2. Die Zufallsauswahl
2.3. Mehrfach-Auswahlverfahren
2.4. Zusammenfassende Übersicht
3. Auswertung von Stichproben: Überblick
3.1. Die Schätzstichproben
3.2. Die Annahmestichproben
4. Schätzen von Anteilswerten
4.1. Entscheidungsregeln für die Wahl des Verfahrens
4.2. Schätzen von Anteilswerten bei Normalverteilung
4.3. Schätzen von Anteilswerten bei Nicht-Normalverteilung
5. Schätzen von Mittelwerten
6. Testen von Hypothesen
6.1. Parametertests für den Anteilswert
6.2. Der sequentielle Hypothesentest
6.3. Verteilungstests: Der Chiquadrat-Anpassungstest
6.4. Unabhängigkeitstest: Der Chiquadrat-Unabhängigkeitstest
7. Zusammenfassende Übersicht
8. Literaturhinweise
© W. Blaas 2006
Vorlesung Inferenzstatistik
3
Kapitel 1: Einleitung
Der Praktiker kann in vielen Fällen nicht gleichzeitig auch ein profunder Kenner der Details
einschlägiger statistischer Methoden sein. Es besteht daher die Notwendigkeit, dem praktisch
Tätigen ein Instrument an die Hand zu geben, welches ihm ein Maximum an RoutineEntscheidungen und -Berechnungen abnimmt und ihn damit in die Lage versetzt, sich rasch und
effizient einer Methode zu bedienen. Die moderne Zielrichtung ist dabei die Erstellung von
Expertensystemen oder Wissensbasierten Systemen, die die Flexibilität und Kompetenz des
Benutzers fördern sollen.
Die folgenden Ausführungen bestehen - inklusive Einleitung - aus sieben Kapiteln. Zunächst
werden die wichtigsten Verfahren der Stichprobenauswahl behandelt (Kapitel 2), wobei die Frage
des Umfanges der Stichproben ausgeklammert und in die einzelnen Methodenkapitel verwiesen
wird. Einen Überblick über die grundsätzlichen Fragestellungen im Zusammenhang mit der
Auswertung von Stichproben gibt dann der nächste Kapitel (3), der auch eine Entscheidungshilfe
für die Wahl der geeigneten Auswertungsmethode je nach den spezifischen Gegebenheiten einer
Stichprobe enthält.
Die beiden nächsten Kapiteln führen in die Methodik des Schätzens von Anteilswerten (Kapitel 4)
sowie von Mittelwerten ein (Kapitel 5).
Die Methode des Testens von Hypothesen ist Gegenstand des nächsten Kapitels (Kap. 6). Hier wird
ausführlich der sogenannte "sequentielle Hypothesentest" dargestellt, der in der praktischen Arbeit
(der Prüfung von Fehlerprozentsätzen) große Vorteile aufweist. Weiters wird der ChiquadratAnpassungstest behandelt.
Abschließend werden die einzelnen Methoden in einer Tabelle zusammengefasst (Kapitel 7).
© W. Blaas 2006
Vorlesung Inferenzstatistik
4
Kapitel 2: Auswahl von Stichproben
In vielen Fällen der Praxis sind Totalerhebungen nicht durchführbar, weil sie zu viel Zeit in
Anspruch nehmen und/oder zuviel Kosten verursachen. Sie sind außerdem dann ganz
auszuschließen, wenn die Prüfung einzelner Elemente mit deren Vernichtung oder Beschädigung
einhergeht (Qualitätskontrolle).
Es ist daher in diesen Fällen erforderlich, eine Teilerhebung oder Stichprobe durchzuführen.
Beispiel: Mikrozensus: quartalsweise Teilerhebung von 1% (ca. 30.000) aller österreichischen
Haushalte (ca. 3 Mio); Volkszählung: Totalerhebung, alle 10 Jahre.
Wir sprechen von der Grundgesamtheit als jener Menge von Elementen, die der Gegenstand der
Untersuchung ist. Jede Folge von Erhebungseinheiten wird als Stichprobe bezeichnet, und die
Länge dieser Folge als Stichprobenumfang. Man sagt, die Stichprobenelemente werden aus der
Grundgesamtheit entnommen, gezogen oder herausgegriffen.
Sind in der Stichprobe bestimmte Merkmalsausprägungen ermittelt worden - z.B. der Anteil
fehlerhafter Elemente oder das arithmetische Mittel eines gewissen Merkmals - so sprechen wir
vom Stichprobenergebnis.
Grundsätzlich kann man Verfahren der einfachen Stichprobenauswahl und der Mehrfach-Auswahl
unterscheiden. Wir befassen uns zunächst mit zwei Varianten der einfachen Stichprobenauswahl,
nämlich der bewussten Auswahl (1. Abschnitt) und der Zufallsauswahl (2. Abschnitt) und danach
mit der Mehrfach-Auswahl (3. Abschnitt).
2.1. Die bewusste Auswahl
Bei der bewussten Auswahl richtet sich der Prüfer nicht nach wahrscheinlichkeitstheoretischen
Erwägungen, sondern nach den beiden folgenden Kriterien:
-
die Bedeutung des einzelnen Prüfungsgegenstandes im Rahmen der Gesamtprüfung
sowohl in absoluter als auch in relativer Hinsicht
das "Fehlerrisiko", also die Wahrscheinlichkeit, mit der bei bestimmten
Stichprobenelementen unzulässige Abweichungen zu erwarten sind.
Beim ersten Kriterium geht man offenbar von der Vorstellung aus, dass - wenn schon nicht die
Gesamtheit prüfbar ist - zumindest jene Elemente aus der Gesamtheit zu prüfen sind, die wegen
ihres Gewichtes oder ihrer Bedeutung das Gesamturteil entscheidend zu beeinflussen in der Lage
sind.
Nach dem zweiten Kriterium soll der Prüfer sein Augenmerk vor allem auf jene Fälle in der
Grundgesamtheit legen, bei denen Fehler (Abweichungen von der Norm) am ehesten zu erwarten
sind.
Auswahltechniken
Im Rahmen der bewussten Auswahl können verschiedene Auswahl- oder Entnahmetechniken
unterschieden werden. Eine Technik, bei der das erste oben genannte Kriterium ("Bedeutung") im
Vordergrund steht, ist die Entnahme nach dem Konzentrationsprinzip. Dabei werden nur solche
© W. Blaas 2006
Vorlesung Inferenzstatistik
5
Elemente aus der Grundgesamtheit ausgewählt, denen der Prüfer besonderes Gewicht beimisst (z.B.
nur Aufträge für Großbauvorhaben).
Beim Verfahren der Auswahl "typischer Fälle" ist hingegen das zweite Kriterium ("Fehlerrisiko")
ausschlaggebend: es werden nur jene Fälle aus der Grundgesamtheit entnommen, von denen der
Prüfer erwartet, dass sie typischerweise fehlerbehaftet sind (z.B. Produkte, die an einem Montag
erzeugt wurden).
Als dritte Technik ist schließlich die sogenante "Klumpenauswahl" zu nennen. Das Prinzip der
Klumpenauswahl besteht darin, im kleinen eine möglichst gute Nachbildung der Grundgesamtheit
hervorzubringen, sozusagen ein Miniaturabbild der zu prüfenden Gesamtheit. Als Beispiel denke
man dabei etwa an die Buchungen im Laufe eines typischen Tages oder Monats: diese Vorgänge
werden dann als repräsentativ für alle Buchungen im betrachteten Gesamtzeitraum (z.B. ein Jahr)
angesehen, sodass der Schluss von der Klumpenauswahl auf die Gesamtheit vertretbar erscheint.
2.2. Die Zufallsauswahl
Die Methoden der zufälligen Auswahl von Stichprobenelementen können danach unterschieden
werden, ob es sich um eine uneingeschränkte Zufallsauswahl oder um eine systematische
Zufallsauswahl handelt.
Uneingeschränkte Zufallsauswahl
Sind die Elemente einer Grundgesamtheit fortlaufend numeriert, so kann das
wahrscheinlichkeitstheoretische Ideal einer uneingeschränkten Zufallsauswahl recht gut durch eine
Auswahl mithilfe von Zufallszahlen angenähert werden.
Zufallszahlen sind entweder entsprechenden Tafeln zu entnehmen (siehe z.B. WETZEL et al., S. 38
ff.), sie können aber auch direkt als Funktion in einem Tabellenkalulationsprogramm (z.B. in
EXCEL) abgerufen werden.
Erzeugen einer Zufallszahl im Intervall [a, b] mithilfe der EXCEL-Funktion ZUFALLSZAHL:
ZUFALLSZAHL().(b-a) + a
(Die Funktion ZUFALLSZAHL() gibt eine zufällige Zahl aus dem Intervall [0, 1] zurück.)
Die Verwendung von Zufallszahlen wird im folgenden Beispiel illustriert.
Beispiel 2.1.
Aufgabenstellung: Aus einer Grundgesamtheit von 1000 durchnumerierten Belegen (Nummern 1
bis 1000) seien 50 zufällig auszuwählen.
© W. Blaas 2006
Vorlesung Inferenzstatistik
6
Ausführung: Man erzeugt mithilfe der EXCEL-Funktion ZUFALLSZAHL() 50 der Größe nach
aufsteigend sortierte Zufallszahlen zwischen 1 und 1000.
Im Detail:
1. Aufruf der EXCEL-Funktion ZUFALLSZAHL(). Diese liegt zwischen 0 und 1.
2. Kopieren, um eine Spalte mit 50 Zufallszahlen zu erhalten.
3. Diese 50 Zufallszahlen in die nächste Spalte kopieren (mit (1) Kopieren; (2) Bearbeiten;
Inhalte einfügen/Werte)
4. In der nächsten Spalte: Multiplikation der Zufallszahlen mit 999 und Addition mit 1.
5. Wiederum in die nächste Spalte kopieren (mit (1) Kopieren; (2) Bearbeiten; Inhalte
einfügen/Werte)
6. Sortieren.
Man verfügt nunmehr über eine aufsteigende Reihe von 50 Zufallszahlen zwischen 1 und 1000. Die
Belege mit diesen Nummern stellen dann die (uneingeschränkt zufällige) Stichprobe dar.

Systematische Zufallsauswahl
Nicht immer ist eine Numerierung der Elemente der Grundgesamtheit möglich oder wirtschaftlich,
sodass das oben beschrieben Verfahren der uneingeschränkten Zufallsauswahl dann nicht
anwendbar ist.
Näherungsweise kann eine Zufallsauswahl dann z.B. durch die sogenannte Buchstabenauswahl
nach Namensanfängen oder durch das Geburtstagsverfahren erfolgen. Im ersten Fall wählt man
z.B. alle Personen, deren Namen mit einem bestimmten Buchstaben beginnt, aus der
Grundgesamtheit aus, im zweiten Fall alle Personen, die an einem bestimmten Tag, Monat oder
Jahr geboren sind.
Voraussetzung für die Anwendbarkeit dieser Hilfsverfahren ist allerdings, dass zwischen den
Auswahlkriterien (Namen; Geburtsdaten) und den zu prüfenden Merkmalen keine Korrelation
besteht. Darüberhinaus ist zu beachten, dass die Namensanfangsbuchstaben bzw. die Geburtsdaten
nicht notwendigerweise gleichmäßig in der Grundgesamtheit verteilt sind.
Als drittes Verfahren, das insbesondere in der Praxis der empirischen Sozialforschung immer
wieder eingesetzt wird, ist das sogenannte Random Walk-Verfahren zu nennen. Dieses Verfahren
besteht darin, dass - z.B. bei einer Befragung auf einer Tribüne - festgelegt wird, jeden 25. Besucher
zu interviewen. Allgemein bedeutet das also, dass jeder k-te Fall (Kunde, Besucher, etc.), dessen
Auftreten zufälliger Natur ist, in die Stichprobe aufgenommen wird.
2.3. Mehrfach-Auswahlverfahren
Die bisher behandelten Auswahlverfahren setzen eine weitgehende Homogenität der
Grundgesamtheit voraus. Ist diese jedoch sehr heterogen oder ist eine Chancengleichheit bei der
Auswahl der Elemente aus erhebungstechnischen Gründen nicht möglich, so muss zu komplexen
Auswahlverfahren übergegangen werden. Das gemeinsame Kennzeichen dieser Verfahren ist es,
dass aus der Grundgesamtheit mehrere Stichproben nach jeweils unterschiedlichen Kriterien
entnommen werden. Dabei ist auch eine Kombination von Zufalls- und von bewusster Auswahl
denkbar.
© W. Blaas 2006
Vorlesung Inferenzstatistik
7
Im folgenden betrachten wir die geschichtete Auswahl einerseits und die mehrstufige Auswahl
andererseits.
Die geschichtete Auswahl
Die geschichtete Auswahl empfiehlt sich, wenn die Grundgesamtheit in Teil-Grundgesamtheiten
(Schichten) zerlegt werden kann, wobei sich diese Zerlegung aus organisatorischen oder
institutionellen Gründen anbietet (z.B. Zerlegung des Bundesgebietes in Bundesländer oder
politische Bezirke) oder wenn sich die Teilmengen bezüglich der zu untersuchenden
Merkmalsausprägung sehr unterscheiden.
Umfasst eine Universität z.B. drei Fakultäten A, B und C, so kann der durchschnittliche
Studienerfolg dadurch erhoben werden, dass in jeder Fakultät (= Schichte) eine Stichprobe
entnommen wird und die jeweiligen Stichprobenmittel zu einem gewichteten Mittel
zusammengefasst werden (ein Rechenbeispiel dazu findet sich etwa bei STENGER, S. 117 f.).
Ist die Schichtung der Grundgesamtheit sowie der insgesamte Stichprobenumfang vorgegeben,
so stellt sich die Frage der Aufteilung der Stichprobe auf die einzelnen Schichten. Im einfachsten
Fall kann diese Aufteilung proportional erfolgen, d.h. der Anteil der jeweiligen Stichprobe
entspricht dem Anteil der Schichte an der Grundgesamtheit.
Sind die Kosten der Erhebung in den einzelnen Schichten sehr unterschiedlich, so bietet sich
aus ökonomischen Gründen eine kostenoptimale Aufteilung der Stichprobe an. Eine solche
Aufteilung ist optimal in dem Sinne, dass sie die Varianz (d.h. den Stichprobenfehler) minimiert
unter Einhaltung einer vorgegebenen, nicht zu überschreitenden Kostengrenze für die Durchführung
der Stichprobe.1
Die mehrstufige Auswahl
Das Prinzip der mehrstufigen Auswahl besteht darin, dass der Prüfer zunächst eine kleine
Stichprobe zieht und aufgrund der Ergebnisse dieser Stichprobe entscheidet, ob er weitere Elemente
aus der Grundgesamtheit entnimmt oder ob er eine hinreichend gut abgesicherte Aussage aus der
bisherigen Stichprobe formulieren kann (usw.).
Der Vorteil eines derartigen Verfahrens liegt vor allem in seiner Wirtschaftlichkeit: die
Erhebung kann in dem Moment abgebrochen werden, in dem eine statistisch zuverlässige Aussage
formulierbar ist.
Als ein Beispiel eines solchen mehrstufigen Auswahlverfahrens werden wir im Kapitel 6 den
sequentiellen Hypothesentest ausführlich behandeln.
2.4. Zusammenfassende Übersicht
Die auf der folgenden Seite zusammengestellte Übersicht fasst die in diesem Kapitel behandelten
Auswahlmethoden nochmals zusammen. Dem Benutzer soll es damit möglich gemacht werden, auf
einen Blick die wichtigsten Auswahlverfahren gegenüberstellen zu können.
1
Die Formel für die Aufteilungsquoten in Abhängigkeit von den jeweiligen Erhebungskosten ist bei STENGER, S. 120
finden.
© W. Blaas 2006
Übersicht 1: Stichprobenauswahl
Zusammenfassende Übersicht
"Stichprobenauswahl"
Mehrfach-Auswahl
(mehrere Stichproben nach
unterschiedlichen Verfahren)
Einfache Stichprobenauswahl
Bewußte Auswahl
(nach Bedeutung und Fehlerrisiko)
Zufallsauswahl
proportional
geschichtete Auswahl
Auswahltechniken
* Konzentrationsprinzip
(Bedeutung)
* typische Fälle
(Fehlerrisiko)
*Klumpenauswahl
(Teilmengen)
uneingeschränkt
(z.B. bei
Numerierung)
systematisch
kostenoptimal
* Buchstabenauswahl
nach Namensanfängen
mehrstufige Auswahl
* Geburtstagsverfahren
* random walk Verfahren
Stichprobe zu klein ->
weitere Stichproben
Kapitel 3: Auswertung von Stichproben: Überblick
Nach dem Untersuchungsziel lassen sich zunächst zwei Arten von Stichproben unterscheiden, und
zwar
*
Schätzstichproben einerseits und
*
Annahmestichproben andererseits.1
3.1. Die Schätzstichproben
Die Auswertung von Schätzstichproben soll statistisch abgesicherte Aussagen über die Struktur der
Grundgesamtheit oder über Merkmalsausprägungen in der Grundgesamtheit möglich machen,
wobei typischerweise etwa folgende Fragen interessieren:
*
*
der Anteil fehlerhafter Elemente in der Grundgesamtheit (Schätzen von Anteilswerten;
siehe unten Kapitel 4)
die Ausprägung eines kardinal-skalierten Merkmals wie z.B. des Mittelwertes (Schätzen
von Mittelwerten; siehe unten Kapitel 5) oder auch anderer Verteilungsparameter.
Dabei unterscheidet man zunächst grundsätzlich zwischen
*
*
Punktschätzungen einerseits und
Intervallschätzungen andererseits.
Bei der Punktschätzung wird für den zu schätzenden Parameter aufgrund des Ergebnisses der
Stichprobe nur ein einziger Schätzwert (Punktschätzwert) angegeben, z.B. der Schätzwert für das
unbekannte arithmetische Mittel mithilfe des arithmetischen Mittels aus der Stichprobe. Man nennt
im Rahmen der Schätztheorie eine derartige Funktion wie etwa das arithmetische Mittel eine
Schätzfunktion.
Wenn man eine Aussage darüber machen möchte, dass ein bestimmter unbekannter Paramter mit
einer gewissen Wahrscheinlichkeit in einem bestimmten Bereich (Intervall) liegt, so verwendet man
die Intervallschätzung. In diesem Falle wird ein sog. Vertrauensintervall oder Konfidenzintervall
ermittelt, das ist ein um den aus der Stichprobe ermittelten Wert liegendes Intervall,
z.B. also p - eu 
P  p + eo
oder
m - eu  µ  m + eo
1
Als eine dritte Art von Stichproben sind die Entdeckungsstichproben zu nennen, die aber im weiteren nicht behandelt
werden. Mit dieser Art der Stichprobe lässt sich die Entdeckungswahrscheinlichkeit von fehlerhaften Elementen in
der Grundgesamtheit berechnen.
Vorlesung Inferenzstatistik
10
innerhalb dessen der "wahre" Wert P bzw µ mit einer gewissen Wahrscheinlichkeit liegt. Die Werte
eu bzw. eo werden als untere bzw. obere Fehlergrenze bezeichnet. Wir befassen uns im folgenden
mit einigen Verfahren der Intervallschätzung.
3.2. Die Annahmestichproben
Die Auswertung von Annahmestichproben soll es andererseits ermöglichen, Hypothesen über die
Struktur der Grundgesamtheit, also über einzelne Parameter statistisch zu testen, oder aber
Hypothesen über die Verteilung als Ganzes statistisch zu testen.
Dementsprechend unterscheidet man
*
*
Parametertests einerseits (siehe Kapitel 6.1 und 6.2) und
Verteilungstests (siehe Kapitel 6.3) andererseits.
Typisch in diesem Zusammenhang ist etwa die Hypothese, dass der Anteil fehlerhafter Elemente in
der Grundgesamtheit einen bestimmten, vorgegebenen Prozentsatz nicht überschreitet; oder etwa,
dass eine empirisch erhobene Verteilung mit einer Gleichverteilung übereinstimmt.
Aus der Vielzahl von weiteren Testverfahren wird weiters ein Verfahren zur Feststellung der
Unabhängigkeit von Merkmalen dargesetllt, und zwar der
*
Chiquadrat-Unabhängigkeits-Test (siehe Kapitel 6.4
Das Verfahren der Annahmestichprobe besteht in der Bestimmung eines Annahme- und eines
Ablehnungsbereiches, die - bei gegebener statistischer Sicherheit - die Annahme oder Ablehnung
einer a priori formulierten Hypothese erlauben.
© W. Blaas 2006
Vorlesung Inferenzstatistik
11
Kapitel 4. Schätzen von Anteilswerten
4.1. Entscheidungsregeln für die Wahl des Verfahrens
Bei betriebswirtschaftlichen Prüfungsaufgaben, wenn es also z.B. um die Überprüfung des Anteils
fehlerloser oder korrekter Elemente in einer Grundgesamtheit geht, ist die Hypergeometrische
Verteilung anzunehmen, weil sie vom zufälligen "Ziehen ohne Zurücklegen" ausgeht, also von
einer Stichprobenanordnung, die i.A. auch der des Prüfers - der keine Interesse hat, ein Element
mehrfach zu prüfen - entspricht.
Dem Vorteil der Übereinstimmung zwischen mathematischem Modell und Stichprobenpraxis steht
bei der Hypergeometrischen Verteilung der Nachteil ihrer rechnerisch schwierigen Handhabbarkeit
gegenüber. Die Wahrscheinlichkeitsverteilung hängt nämlich von den drei Parametern (1) Umfang
der Grundgesamtheit N, (2) Stichprobenumfang n und (3) Anzahl A der fehlerhaften Elemente in
der Grundgesamtheit ab (siehe Kapitel „Wahrscheinlichkeitsverteilungen“).
Dieses derzeit noch in vielen Lehrbüchern verwendete Argument verliert jedoch mit zunehmender
Leistungsfähigkeit der PC-Hardware und -Software immer mehr an Relevanz. So kann man sich
z.B. der EXCEL-Funktion HYPGEOMVERT bedienen, um auf einfache und schnelle Weise die
Werte der Wahrscheinlichkeitsfunktion sowie jene der Verteilungsfunktion zu ermitteln.
In der Praxis der Schätzverfahren geht man allerdings von Bedingungen der Stichproben aus, die es
erlauben, andere Wahrscheinlichkeitsverteilungen als Näherung an die Hypergeometrische
Verteilung zu verwenden. Dabei geht es (1) um den Umfang der Stichprobe n; (2) um die
Stichprobenquote n/N, also das Verhältnis des Stichprobenumfangs zum Umfang der
Grundgesamtheit und (3) um die Größe des Anteilswertes p.
Im folgenden Flussdiagramm ist eine Entscheidungsabfolge wiedergegeben, mit Hilfe derer
entschieden werden kann, welches der in weiterer Folge beschriebenen Verfahren der Ermittlung
von Konfidenzintervallen für Anteiswerte verwendet werden kann.
© W. Blaas 2006
Vorlesung Inferenzstatistik
Abbildung 4.1:
12
Entscheidungsregeln für die Auswahl des Verfahrens zur Ermittlung von
Konfidenzintervallen von Anteilswerten
Start
Voraussetzungen:
(1) n/N "klein", d.h. n/N < 0.1
(2) n "groß", d.h. n > 30
p<0.1
Schätzen von
Anteilswerten bei
Nicht- Normalverteilung
Quelle: Eigene Darstellung, 12.4.2000
© W. Blaas 2006
p>0.1
Schätzen von
Anteilswerten bei
Normalverteilung
Vorlesung Inferenzstatistik
4.2.
13
Schätzen von Anteilswerten bei Normalverteilung
Wir haben gesehen, dass im Falle des Schätzens von Anteilswerten die Hypergeometrische
Verteilung durch die Normalverteilung dann angenähert werden kann, wenn der
Stichprobenumfang groß ist (n30) und der Anteilswert nicht zu klein ist (p>0.1).
Wenn wir nun annehmen, dass dies der Fall sei, so vereinfacht sich die Ermittlung des
Konfidenzintervalles
p - eu  P  p + eo
[4.1]
wegen der Symmetrie der Normalverteilung zu
p - e  P  p + e.
[4.2]
Der Stichprobenfehler e ist in Abhängigkeit vom Stichprobenergebnis (p), dem Stichprobenumfang
(n) und dem Sicherheitsgrad (w) bzw. dem davon abgeleiteten Quantil der Normalverteilung (t) wie
folgt zu berechnen:
p.(1  p)
n
[4.3]
p.(1  p)
p.(1  p)
, p  t.
]
n
n
[4.4]
e  t.
Das gesuchte Konfidenzintervall ist daher
[ p  t.
Hinweis: zwei trade-off’s
(1) Kosten versus Genauigkeit (Stichprobenumfang n)
(2) Genauigkeit versus Sicherheit
© W. Blaas 2006
Vorlesung Inferenzstatistik
14
Die Fraktile der Normalverteilung (t) für die am häufigsten verwendeten Sicherheitsgrade (w) sind
im folgenden zusammengestellt:
Tabelle 4.1.: Schranken der Normalverteilung [= -STANDNORMINV((1-w)/2)]
w (%)
90,00%
95,00%
95,50%
99,00%
99,70%
99,90%
Schranke t
1,64
1,96
2,00
2,58
3,00
3,29
Schranke heißt, dass eine standardnormalverteilte Zufallsvariable mit 90%-iger Wahrscheinlichkeit
zwischen -1,64 und +1,64 liegt (Daher ist das Ablesen der 0,05-Quantile bzw. der 0,95-Quantile
erforderlich: STANDNORMINV(0,05)=-1,64).
Rechenbeispiel 4.1.
Gegeben seien folgende Daten:
Stichprobenumfang n:
Grundgesamtheit N:
Stichprobenergebnis p:
235
8716
0.11.
Zu ermitteln ist ein Konfidenzintervall, innerhalb dessen mit einer Wahrscheinlichkeit von 95% der
"wahre" Anteilswert liegt.
Unter Verwendung der Tabelle 4.1. und Ausdruck [4.4] erhält man für das Konfidenzintervall:
[0,069995, 0,150004].
Mit anderen Worten: der wahre Wert des Anteils (fehlerhafter Elemente) liegt mit 95%-iger
Sicherheit zwischen 6.9% und 15.0%.
Das Ergebnis hängt nicht unwesentlich vom verlangten Sicherheitsgrad w ab. Fordern wir etwa eine
99.9%-ige Wahrscheinlichkeit für das Konfidenzintervall, so vergrößert sich das Intervall auf
[4.3%, 17.7%]. Zwischen der Sicherheit und der Genauigkeit der Schätzung besteht also ein
inverser Zusammenhang bzw. ein trade-off: je größer die Sicherheit, umso ungenauer, je genauer,
umso unsicherer die Aussage.

© W. Blaas 2006
Vorlesung Inferenzstatistik
15
Im obigen Beispiel ist der Stichprobenumfang n in Verhältnis zum Umfang der Grundgesamtheit N
klein (ungefähr 2.5%). Liegt diese Stichprobenquote zwischen 5% und 10%, ist also der
Stichprobenumfang im Verhältnis zur Grundgesamtheit größer, so muss der Ausdruck [4.3] durch
den Faktor (N-n)/(N-1) korrigiert werden:
e  t.
p(1  p) ( N  n)
.
n
( N  1)
[4.5]
Rechenbeispiel 4.2.
Unter den gleichen Annahmen wie im Rechenbeispiel 4.1., jedoch bei einer Grundgesamtheit von N
= 3721 ergibt sich dann nach Formel [4.5] ein mit dem Korrekturfaktor ermitteltes
Konfidenzintervall
[0.071273, 0.148726].

Stichprobenumfang
Löst man die Formel [4.3] nach n auf, so kann man den für eine vorgegebene Sicherheit (w) und
Genauigkeit (e) erforderlichen Stichprobenumfang ermitteln:
n
Dazu ist allerdings notwendig,
Stichprobenergebnis (p) trifft.
dass
t 2 . p(1  p)
e2
man
eine
[4.6]
Annahme
über
das
zu
erwartende
Die Annahme über p kann abgeleitet werden aus
(1) einer Schätzung von p aufgrund früherer Erfahrungen mit ähnlichen Stichproben;
(2) einer Schätzung von p aus einer Vorstichprobe (Pilot-Studie);
(3) der Unterstellung der ungünstigsten Konstellation: der Wert von p wird z.B. mit 0.5
(50% Fehleranteil) angenommen;
(4) der Feststellung eines höchstzulässigen Fehleranteiles.
Für die Bestimmung des Stichprobenumfanges n ist also die Vorgabe des Sicherheitsniveaus w
(und damit t), die verlangte maximale Fehlermarge e sowie eine Annahme über das
Stichprobenergebnis p erforderlich.
© W. Blaas 2006
Vorlesung Inferenzstatistik
16
Rechenbeispiel 4.3.:
Der Wähleranteil einer Partei, der in der Größenordnung von 12% liegt, soll durch eine Stichprobe
bis auf eine maximale Ungenauigkeit von  1% geschätzt werden (bei  = 0,05). Es wird also ein
95%-iges Konfidenzintervall für den Anteilswert gesucht. Wie groß muss die Stichprobe sein?
Es gilt:
e = 0.01
p = 0.12
w = 95%.
Durch Einsetzen der Formel [4.6] ergibt sich:
n = 4057.
Reduziert man die verlangte Genauigkeit e, z.B. auf 2% (gegenüber den ursprünglichen 1%), so
genügt eine wesentlich kleinere Stichprobe, nämlich
n = 1014.

© W. Blaas 2006
Vorlesung Inferenzstatistik
17
4.3. Schätzen von Anteilswerten bei Nicht-Normalverteilung
Ist der erwartete Fehleranteil in der Grundgesamtheit kleiner als 10%, so ist - gemäß dem
Entscheidungsdiagramm 4.1 - die Annäherung der Hypergeometrischen Verteilung durch die
Normalverteilung nicht zulässig. Ist der Stichprobenumfang nicht zu klein (n  30), so kann die
Poisson-Verteilung statt dessen verwendet werden. Die Poisson-Verteilung ist im Gegensatz zur
Normalverteilung asymmetrisch, sodass die obere und untere Grenze des Konfidenzintervalls
separat berechnet werden müssen. Da bei (betriebs-) wirtschaftlichen Prüfungen aber i.A. nur die
obere Fehlergrenze interessiert, genügt es meist, diese zu ermitteln.
Für die Bestimmung der Obergrenze po verwendet man die Beziehung
n.po = 0.5.2w;f .
[4.8]
Aus [4.8] ergibt sich daher für po:
po = 0.5.2/n .
[4.9]
Die jeweiligen Quantile der 2-Verteilung können entweder mithilfe der EXCEL-Funktion CHIINV
abgelesen werden oder aus einer Tabelle entnommen werden (siehe z.B. WETZEL et al.). Dabei
sind die Parameter der 2-Verteilung einerseits der Sicherheitsgrad w, andererseits der Freiheitsgrad
f. Der Freiheitsgrad ist aus dem Stichprobenergebnis zu berechnen, und zwar aus der Absolutzahl m
der fehlerhaften Elemente in der Stichprobe:
f = 2.(m+1).
Rechenbeispiel 4.4.
Aus einer Grundgsamtheit der Größe N=7500 sei eine Stichprobe mit dem Umfang n=520
entnommen worden, wobei m=6 fehlerhafte Elemente festgestellt wurden. Mit einer
Wahrscheinlichkeit von 95% soll die maximale Anzahl der fehlerhaften Elemente in der
Grundgesamtheit ermittelt werden. Es gilt also:
N = 7500
n = 520
m = 6; daher f = 14
w = 95%.
Aus der Tabelle der 2-Verteilung ergibt sich für 20.95;14 = 23.685 [EXCEL: CHIINV(0,05;14)].
Somit ist gemäß [4.9]
po = 0.02277 = 2.28%.
Ergebnis: Mit einer Aussagesicherheit von 95% kann gesagt werden, dass der Anteil der
fehlerhaften Elemente in der Grundgesamtheit nicht größer als 2.28% ist, oder, dass nicht mehr als
(N.po =) 171 Elemente fehlerhaft sind.

© W. Blaas 2006
Vorlesung Inferenzstatistik
18
Kapitel 5: Schätzen von Mittelwerten
Bei der Schätzung von Mittelwerten kann man, vorausgesetzt, die Stichprobe ist genügend groß,
grundsätzlich von einer Normalverteilung der Stichprobenergebnisse ausgehen.
Das arithmetische Mittel (einer bestimmten Merkmalsausprägung) aller Elemente der
Grundgesamtheit,
µ =
 Aj/N ,
j = 1, N .
[5.1]
schätzt man durch das arithmetische Mittel sämtlicher Elemente ai der Stichprobe:
m =  ai/n .
i = 1, n .
[5.2]
Wegen der Symmetrie der Normalverteilung ist das dazugehörige Konfidenzintervall gegeben
durch die Beziehung
m-e µ m+e.
[5.3]
Der Stichprobenfehler e (mit Korrekturfaktor) wird nach der Formel [5.4] berechnet:
e  t.
 2 .( N  n)
[5.4]
n.( N  1)
wobei t wiederum der gemäß dem Sicherheitsgrad w ermittelte Funktionswert der Normalverteilung
ist (siehe Kapitel 4, Tabelle 4.1.).
Die für die Berechnung der Formel [5.4] erforderliche Varianz 2 ist im allgemeinen nicht bekannt
und muss daher durch die Stichprobenvarianz s2 angenähert werden:
s2 =  (ai-m)2/n .
i = 1, n.
[5.5]
Durch Einsetzen von [5.5] in [5.4] und [5.4] in [5.3] erhält man schließlich das mit den
Stichprobenergebnissen berechenbare Konfidenzintervall
m  t.
s 2 .( N  n)
n.( N  1)
[5.6]
und ohne Berücksichtigung des Korrekturfaktors, wenn also die Stichprobenquote n/N kleiner als
oder höchstens gleich 5% ist,
m  e  m  t.
© W. Blaas 2006
s2
n
[5.7]
Vorlesung Inferenzstatistik
19
Rechenbeispiel 5.1.
Aus einer Grundgesamtheit von 4500 Einheiten wird eine Stichprobe von 150 Einheiten
entnommen und das arithmetische Mittel einer bestimmten Merkmalsausprägung sowie die
Stichprobenvarianz berechnet. Deren Werte seien m = 75 bzw. s2= 82. Es soll mit 95%-iger
Sicherheit ein Konfidenzintervall für den "wahren" Mittelwert µ angegeben werden.
Die Stichprobenquote n/N ist in diesem Falle kleiner als 5%, sodass Formel [5.7] zur
Anwendung gelangt. Die Lösung ist das Intervall
[73.55, 76.45].
Nehmen wir an, dass ein Stichprobenumfang von n = 500 unter den identischen Bedingungen zu
den gleichen Mittel- und Varianzwerten geführt hätte, so ist das gesuchte Konfidenzintervall
aufgrund der Formel [5.6] zu ermitteln und ergibt sich zu
[74.252, 75.748].

© W. Blaas 2006
Vorlesung Inferenzstatistik
20
Ergänzung: Verwendung der EXCEL-Funktion KONFIDENZ
Die Funktion KONFIDENZ Ermöglicht die Berechnung des Fehlerterms e eines 1-Alpha
Konfidenzintervalls für den Erwartungswert einer Zufallsvariablen (Achtung: nicht geeignet für die
Ermittlung eines Konfidenzintervalles für Anteilswerte!)
Syntax: KONFIDENZ(Alpha;StandardAbweichung;Umfang)
KONFIDENZ  e  t.
s
n
Alpha ist die Irrtumswahrscheinlichkeit bei der Berechnung des Konfidenzintervalls. Das
Konfidenzintervall ist gleich 100*(1 - Alpha)%, was bedeutet, dass ein Wert für Alpha von 0,05
einem Konfidenzniveau von 95% entspricht. StandardAbweichung ist die als bekannt
angenommene Standardabweichung der Grundgesamtheit. Umfang ist der Umfang der Stichprobe.
Hinweise
· Ist eines der Argumente nichtnumerisch, gibt KONFIDENZ den Fehlerwert #WERT!
zurück.
· Ist Alpha  0 oder Alpha  1, KONFIDENZ den Fehlerwert #ZAHL! zurück.
· Ist StandardAbweichung  0, KONFIDENZ den Fehlerwert #ZAHL! zurück.
· Ist Umfang keine ganze Zahl, wird der Dezimalanteil abgeschnitten.
· Ist Umfang < 1, KONFIDENZ den Fehlerwert #ZAHL! zurück.
· Ist Alpha gleich 0,05, dann muss die Fläche unter der Kurve der standardisierten
Normalverteilung berechnet werden, die dem Wert (1 - Alpha) bzw. 95% entspricht. Dieser
Wert ist ± 1,96. Für das Konfidenzintervall gilt daher:
  
m  1,96

 n
Beispiel
Angenommen, eine Stichprobe bei 50 Berufspendlern ergibt, dass diese im Mittel 30 Minuten
benötigen, um zu ihrem Arbeitsplatz zu gelangen, wobei die Standardabweichung der
Grundgesamtheit 2,5 beträgt. Dann gilt mit einer Wahrscheinlichkeit von mindestens 95%, dass der
Mittelwert der Grundgesamtheit im folgenden Intervall liegt:
 2,5 
30  1,96

 50 
oder:
KONFIDENZ(0,05;2,5;50) ist gleich 0,692951. Dies bedeutet eine mittlere Fahrzeit zur Arbeit 30
Minuten ± 0,692951 Minuten, also zwischen 29,3 und 30,7 Minuten.

© W. Blaas 2006
Vorlesung Inferenzstatistik
21
Stichprobenumfang
Die Frage des Stichprobenumfanges, der bei einem vorgegebenen zulässigen Fehler e und
gegebenem Sicherheitsgrad w erforderlich ist, kann wiederum aus den Beziehungen [5.6] bzw. [5.7]
abgeleitet werden.
Danach ergibt sich für den Stichprobenumfang n mit Korrekturfaktor
n
t 2 . N . s2
t 2 . s 2  e 2 .( N  1)
[5.8]
und ohne Korrekturfaktor
t 2 . s2
n 2
e
[5.9]
Rechenbeispiel 5.2.
Es seien folgende Angaben gültig:
N = 4500
e = 1.80
s2= 65
w = 95%.
Durch Anwendung der Beziehung [5.8] ergibt sich für den Stichprobenumfang mit Korrekturfaktor
n = 76,
unter Verwendung der Beziehung [5.9] der Stichprobenumfang ohne Korrekturfaktor
n = 77.

© W. Blaas 2006
Vorlesung Inferenzstatistik
22
Kapitel 6: Testen von Hypothesen
Im Rahmen der Testverfahren wird die Frage behandelt, wie man mithilfe von (Zufalls-)
Stichproben testen (überprüfen) kann, ob bestimmte Hypothesen (Annahmen, Behauptungen) über
eine unbekannte Grundgesamtheit richtig oder falsch sind.
Ein statistischer Test ist also ein Verfahren, das es erlaubt, bestimmte Hypothesen auf ihre
Richtigkeit hin zu überprüfen.
Im Folgenden befassen wir uns mit drei Arten von Hypothesen:
1.
Hypothesen
über
unbekannte
Parameter
einer
Grundgesamtheit,
Parameterhypothesen, die mit Parametertests überprüft werden;
2. Hypothesen über die unbekannte Verteilungsform einer Grundgesamtheit,
Verteilungshypothesen, die mit Verteilungstests überprüft werden.
3. Hypothesen
zur
Abhängigkeit
Unabhängigkeitstests.
oder
Unabhängigkeit
von
Merkmalen
sog.
sog.
–
6.1. Parametertests für den Anteilswert: Grundbegriffe für Testverfahren
Wenn aufgrund normativer Vorgaben der höchstzulässige Fehleranteil in der Grundgesamtheit
gegeben ist, so kann man bei gegebenem Sicherheits- und Genauigkeitsgrad der statistischen
Aussage jene Anzahl der fehlerhaften Elemente (m) bei gegebenem Stichprobenumfang (n)
berechnen, die gerade noch zur "Annahme" der Grundgesamtheit berechtigen. Umgekehrt kann die
Zahl der fehlerhaften Elemente, die zu einer "Ablehnung" der Grundgesamtheit berechtigen,
ermittelt werden.
Während die Schätzstichprobe also dazu verwendet wird, effektive Schätzwerte zu berechnen, dient
die Annahmestichprobe der Ermittlung sogenannter "Annahme-" bzw. "Ablehnungs-Bereiche".
Hat der Prüfer z.B. eine Vermutung über den Anteil fehlerhafter Elemente in der Grundgesamtheit
oder hat er diese auf einen bestimmten Fehleranteil hin zu untersuchen, so kann er diese Tatsache
als Hypothese formulieren. Man nennt diese die sogenannte "Nullhypothese" H0:
H0: P = p0;
sie besagt, dass nach der vom Prüfer verwendeten Ausgangshypothese der "wahre" Fehleranteil in
der Grundgesamtheit (P) gleich dem Anteil fehlerhafter Elemente in der Stichprobe (p0) ist.
Zu jeder Nullhypothese kann eine Gegenhypothese H1 formuliert werden, und zwar entweder in
nicht konkretisierter Form
H1: P  p0
oder in konkretisierter Form
H1: P = p1.
© W. Blaas 2006
Vorlesung Inferenzstatistik
23
In der Praxis empfiehlt es sich, die Gegenhypothese zu konkretisieren, denn dann ist es in jedem
Falle möglich, den sog. Sicherheitsgrad (w) bzw. dessen Gegenwahrscheinlichkeit (1-w) zu
berechnen, das ist die Irrtumswahrscheinlichkeit, mit der die Nullhypothese abgelehnt wird oder
nicht abgelehnt wird.
Dem Prüfer können zwei unterschiedliche Arten von Fehlurteilen unterlaufen. Erstens kann er
aufgrund der Stichprobe die Nullhypothese ablehnen, obwohl sie auf die Grundgesamtheit zutrifft,
also "wahr" ist. Dieses Fehlurteil wird Fehler 1. Art genannt und die Wahrscheinlichkeit, einen
derartigen Fehler zu begehen, bezeichnen wir mit  oder -Risiko. In der Literatur spricht man auch
vom Risiko des Prüfungsauftraggebers: eine ordnungsgemäße Grundgesamtheit wird aufgrund der
Stichprobe abgelehnt. Das -Risiko entspricht der Irrtumswahrscheinlichkeit (1-w0) bei einer
konkretisierten Gegenhypothese.
Das zweite mögliche Fehlurteil besteht in der Annahme einer "falschen" Nullhypothese. Dieser Fall
wird als Fehler 2. Art bezeichnet, und die Wahrscheinlichkeit, einen solchen Fehler zu begehen, als
 bzw. -Risiko. Dieses Risiko wird auch das Risiko des Prüfers genannt, weil es die
Irrtumswahrscheinlichkeit beschreibt, mit der der Prüfer eine nicht ordnungsgemäße
Grundgesamtheit annimmt.
Tabelle 6.1.: Entscheidungssituation des Prüfers (WYSOCKI [3], S. 206)
In der Grundgesamtheit
gilt tatsächlich:
H0 ist richtig
Urteil aufgrund der
Stichprobe:
H0 wird angenommen
H1 wird angenommen
© W. Blaas 2006
richtiges Urteil
falsches Urteil
-Produzenten-Risiko
H1 ist richtig
falsches Urteil
-Prüfer-Risiko
richtiges Urteil
Vorlesung Inferenzstatistik
24
Für die Durchführung des Tests hat der Prüfer konkrete Werte von  und  festzulegen. Im
allgemeinen genügt es durchaus, für das -Risiko eine Höhe von =0.05 anzunehmen. Dies
entspricht einer statistischen Sicherheit der Aussage von 95%.
Hinsichtlich des -Risikos kann man entweder so verfahren, dass man die gleiche Höhe wählt wie
beim -Risiko, oder aber, weil es das für den Prüfer gefährlichere Risiko ist, einen geringeren Wert
ansetzt (z.B. =0.01).
Das eigentliche Testverfahren besteht nun darin, einen Annahmebereich und einen
Ablehnungsbereich (Verwerfungsbereich; kritischer Bereich) für die Nullhypothese zu ermitteln.
Diese Bereiche lassen sich bei Kenntnis der Null- sowie der Gegenhypothese, des -Risikos und
des -Risikos, sowie der Stichprobendaten bestimmen.
Im folgenden Abschnitt wird ein solches Testverfahren vollständig anhand des Sequentiellen
Hypothesentests nach WALD beschrieben.
6.2. Der sequentielle Hypothesentest
Der sequentielle Hypothesentest gehört zur Klasse der Parametertests, mit denen Aussagen über
einzelne Parameter (Anteilswerte, Mittelwerte) oder Parameter-Differenzen geprüft werden können
(siehe dazu Abschnitt 3 unten).
Im Falle des sequentiellen Hypothesentests geht es um die Prüfung eines Anteilwertes in der
Grundgesamtheit, z.B. also um den Anteil fehlerhafter Buchungen. Mithilfe einer Stichprobe soll
festgestellt werden, ob eine den Fehleranteil betreffende Nullhypothese H0 angenommen werden
kann oder verworfen werden muss.
Der Vorteil des sequentiellen Hypothesentests gegenüber anderen in diesem Falle einsetzbaren
Tests besteht darin, dass er (im Durchschnitt) kostensparender, also wirtschaftlicher als andere
Tests ist. Es ist nämlich nicht erforderlich, von einem im voraus bestimmten Stichprobenumfang
auszugehen, sondern dieser kann - bei gegebenem Sicherheits- und Genauigkeitsniveau - während
des Verfahrens aus den Ergebnissen der Stichprobenziehungen festgelegt werden, sodass ein
minimaler Stichprobenumfang, und damit minimale Kosten der Stichprobenerhebung, gewährleistet
sind.
Das Verfahren kann wie folgt beschrieben werden (siehe dazu Abbildung 6.1.):
1.
Die Zufallsstichprobe wird nicht im ganzen gezogen, sondern die einzelnen Elemente
werden sukzessive aus der Grundgesamtheit entnommen, wobei nach der Prüfung jedes
einzelnen Falles (oder einer Gruppe von Elementen) entschieden wird, ob weitere
Stichprobenelemente gezogen werden müssen oder nicht.
2.
Nach jeder Entnahme eines Stichprobenelementes bzw. einer Gruppe von Elementen ist
eine der drei folgenden Entscheidungen zu treffen:
a.
Erreicht oder überschreitet die unter den bisherigen Stichprobenelementen vorgefundene
Zahl fehlerhafter Elemente (m) eine in Abhängigkeit vom Stichprobenumfang (n)
berechnete Ablehnungszahl z, gilt also mz, so ist die Grundgesamtheit (als fehlerhaft)
zurückzuweisen.
© W. Blaas 2006
Vorlesung Inferenzstatistik
b.
c.
3.
25
Erreicht oder unterschreitet die in den bisherigen Stichprobenelementen vorgefundene
Zahl fehlerhafter Elemente (m) eine in Abhängigkeit vom Stichprobenumfang (n)
berechnete Annahmezahl a, gilt also ma, so ist die Grundgesamtheit (als ordnungsgemäß)
anzunehmen.
Liegt die Zahl der unter den bisherigen Stichprobenelementen vorgefundenen fehlerhaften
Elementen (m) zwischen der Annahme- und der Ablehnungszahl, gilt also a<m<z, so ist
ein weiteres Element aus der Grundgesamtheit zu entnehmen.
Die Entnahme von Stichprobenelementen wird solange fortgesetzt, bis eine eindeutige
Annahme oder Ablehnung (der Nullhypothese) möglich ist.
Der Annahme- und der Ablehnungsbereich sind beim sequentiellen Hypothesentest also vom
Stichprobenumfang abhängig, sie verändern sich daher mit zunehmendem Stichprobenumfang. Die
Annahmezahl a und die Ablehnungszahl z werden bei gegebener Nullhypothese (H0=p0),
Gegenhypothese (H1=p1), bei gegebenem -Risiko und -Risiko nach den Ausdrücken [6.1] und
[6.2] bestimmt:
a = - hu + s.n
[6.1]
z = ho + s.n
[6.2]
mit
ln
hu 
ln
ho 
1 

P1.(1  P0)
P0.(1  P1)
ln
1 

P1.(1  P0)
ln
P0.(1  P1)
1  P0
1  P1
s
P1.(1  P0)
ln
P0.(1  P1)
ln
© W. Blaas 2006
Vorlesung Inferenzstatistik
26
Abbildung 6.1.: Flussdiagramm des sequentiellen Hypothesentests
Start
Bestimmung der Annahmezahlen (a) und der
Ablehnungszahlen (z) für alle
Stichprobenumfänge (n) aus P0, P1, a und b
Ziehen und Auswerten eines (weiteren)
Stichprobenelementes bzw. einer (weiteren)
Gruppe von Stichprobenelementen
ja
1?
Nullhypothese
annehmen
Ende
nein
ja
2?
Nullhypothese
ablehnen
Ende
nein
weiterprüfen!
Legende:
1. Anzahl bisher ermittelter fehlerhafter Elemente (m) kleiner als die dem
erreichten Stichprobenumfang (n) entsprechende Annahmezahl (a) ?
2. Anzahl bisher ermittelter fehlerhafter Elemente (m) größer als die dem
erreichten Stichprobenumfang (n) entsprechende Ablehnungszahl (z) ?
Quelle: WYSOCKI [3], S. 209
© W. Blaas 2006
Vorlesung Inferenzstatistik
27
Wie aus den Gleichungen [6.1] und [6.2] ersichtlich ist, können der Annahme- und der
Ablehnungsbereich als lineare Funktionen des Stichprobenumfanges n (das sind Geraden mit der
Steigung s) aufgefasst werden.
Rechenbeispiel 6.1.
Gehen wir von folgenden Voraussetzungen aus: Hinsichtlich des akzeptablen Fehleranteils sei eine
Nullhypothese in der Höhe von 1%, eine Gegenhypothese in der Höhe von 5% formuliert worden.
Das Auftraggeber-Risiko (-Risiko) sei mit 5%, das Prüferrisiko (-Risiko) sei mit 1% vorgegeben.
Es gilt daher:
H0 (Nullhypothese)
H1 (Gegenhypothese)
 (Auftraggeber-Risiko)
 (Prüferrisiko)
= 0.01 (= p0)
= 0.05 (= p1)
= 0.05
= 0.01
Lösung:
Die Anwendung der Formeln [6.1] und [6.2] ergibt
ho = 1.808758
hu = 2,758787
s = 0.024985
und somit folgende Gleichungen für die Annahmegerade (a) und die Ablehnungsgerade (z):
a = - 2.758787 + 0.024985.n
z = 1.808758 + 0.024985.n
Die beiden Geraden sind in der Abbildung 6.2. dargestellt. Sie spannen den zwischen ihnen
liegenden Prüfbereich auf, der jene Stichprobenergebnisse enthält, die zu weiteren StichprobenEntnahmen veranlassen.
Abbildung 6.2. zeigt, dass der Stichprobentest nach der Prüfung des 111. Elementes (mit positivem
Ergebnis) abgebrochen werden kann, wenn bis dahin kein fehlerhaftes Element aufgetreten ist. Ist
bis zum 151. Element nur ein fehlerhaftes Element aufgetreten, so kann der Test ebenfalls bei
Annahme der Nullhypothese abgebrochen werden usw.
© W. Blaas 2006
Vorlesung Inferenzstatistik
Abbildung 6.2.:
28
Annahme-, Prüf- und Ablehnungsbereich
beim sequentiellen Hypothesentest
( = 0.05;  = 0.01)
Vorlesung Inferenzstatistik
29
Im Vergleich dazu zeigt Abbildung 6.3. den Annahme-, Prüfungs- und Ablehnungsbereich bei sonst
gleichen Vorgaben, aber bei ==0,05. Man sieht, wie unter diesen weniger strengen
Sicherheitsvorgaben der Annahmebereich deutlich größer wird (d.h. die Annahmegerade verschiebt
sich parallel nach oben). In diesem Falle kann der Test bei Annahme der Nullhypothese schon nach
der Prüfung des 72. Elementes abgebrochen werden, wenn bis dahin kein fehlerhaftes Element
aufgetreten ist. Ist bis zum 112. Element nur ein fehlerhaftes Element aufgetreten, so kann der Test
ebenfalls mit positivem Ergebnis abgebrochen werden usw.
Hinweis (Übung):
Überprüfe die Veränderungen des Annahme-, des Prüf- und des Ablehnungsbereiches, wenn die
Differenz zwischen Null- und Gegenhypothese (H0 und H1) vergrößert/verkleinert wird, und wenn
 bzw.  variieren.
© W. Blaas 2006
Vorlesung Inferenzstatistik
Abbildung 6.3.:
30
Annahme-, Prüf- und Ablehnungsbereich
beim sequentiellen Hypothesentest
( = 0.05;  = 0.05)
Ablehnungsbereic
h
Prüfbereich
Annahmebereich
Vorlesung Inferenzstatistik
31
6.3. Verteilungstests: Der Chi-Quadrat-Anpassungstest
Bei der Prüfung einer Verteilungshypothese untersucht man, ob die in einer Stichprobe festgestellte
Verteilung mit der für die unbekannte Verteilung angenommenen theoretischen Verteilung in
Widerspruch steht oder nicht. Oder anders ausgedrückt: Man entscheidet, ob die Unterschiede, die
man zwischen der empirisch festgestellten und der theoretisch angenommenen Verteilung noch dem
Zufall zugeschrieben werden können oder nicht.
Da es dabei um die Güte der Anpassung der empirischen an eine theoretische Verteilung geht,
spricht man auch von Anpassungstests.
Ein sehr gebräuchliches Verfahren zur Prüfung von Verteilungshypothesen ist der Chi-QuadratTest (auch: Chiquadrat-Anpassungstest). Die Nullhypothese lautet immer, dass die Grundgesamtheit
einer bestimmten Verteilung gehorcht.
Wir besprechen den Chi-Quadrat-Test anhand eines einfachen Beispiels einer diskreten (Gleich-)
Verteilung der Grundgesamtheit:
1.
Beim 90-maligen Werfen eines Würfels seien folgende Häufigkeiten der Augenzahlen
beobachtet worden (hib):
Augenzahl i
abs. Häufigkeit hib
2.
1
19
2
13
3
14
4
12
5
17
6
15
Null- und Alternativhypothese und Signifikanzniveau
H0: : Die Augenzahlen sind gleichverteilt
H1: : Die Augenzahlen sind nicht gleichverteilt
 = 0,05.
3. Prüfgröße und Testverteilung
Bei Gültigkeit der Nullhypothese wären die erwarteten absoluten Häufigkeiten (expected)
hie = 90/6 = 15. Die folgende Tabelle enthält die beobachteten und die erwarteten
absoluten Häufigkeiten der Augenzahlen:
Augenzahl i
hib
hie
1
19
15
2
13
15
3
14
15
4
12
15
5
17
15
6
15
15
Es lässt sich zeigen, dass die Prüfgröße PG
PG =  ( hib - hie)2/hie i = 1,k
näherungsweise einer Chi-Quadrat-Verteilung mit (k-1) Freiheitsgraden folgt, wobei k die
Anzahl der Merkmalsausprägungen (= Anzahl der Elementarereignisse bei einmaliger
Durchführung des Experimentes) ist.
Voraussetzung für die Anwendung der Chi-Quadrat-Verteilung ist allerdings, dass die
erwarteten absoluten Häufigkeiten nicht zu klein sind, wobei als Faustregel hie  5 gilt. (In
© W. Blaas 2006
Vorlesung Inferenzstatistik
32
Fällen, wo dies nicht gegeben ist, müssen vor Anwendung des Tests Merkmalsklassen zu
stärker besetzten Klassen zusammengefasst werden).
4.
Annahme- und Ablehnungsbereich
Aus der Tabelle der Chi-Quadrat-Verteilung erhält man für das Signifikanzniveau  = 0,05
und (k-1) = 5 Freiheitsgraden den kritischen Wert 20,95; 5 = 11,07
[EXCEL: CHIINV(0,05; 5)=11,07].
Für PG > 11,07 ist die Nullhypothese abzulehnen, für PG  11,07 kann die Nullhypothese
nicht abgelehnt werden.
5.
Berechnung der Prüfgröße
PG = 2,267
6.
Entscheidung und Interpretation
Da die Prüfgröße PG  20,95; 5, kann die Nullhypothese "die Augenzahlen sind
gleichverteilt", nicht abgelehnt werden.
© W. Blaas 2006
Vorlesung Inferenzstatistik
33
6.4. Der Chi-Quadrat-Unabhängigkeitstest
Ein häufig verwendetes Testverfahren, das mit einer ähnlichen Methode vorgeht, ist der häufig
angewandte Chi-Quadrat-Unabhängigkeitstest.
Mit ihm lässt sich beispielsweise testen, ob zwei nominalskalierte (qualitative) Merkmale
voneinander unabhängig sind oder nicht.
Die Methode wird wieder anhand eines Beispiels erläutert.
Eine Stelle sei ausgeschrieben worden, für die sowohl HTL-Ingeneure, FH-Ingenieure als auch
Dipl.Ingeneure geeignet sein könnten. Es bewerben sich 30 HTL-AngängerInnen, 35 FHAbsolventInnen und 35 Universitätsabsolventinnen. Nach einem Eignungstest werden 14 HTL-, 10
FH- und 16 Diplomingenieure als geeignet qualifiziert.
Merkmal A: geeignet; ungeeignet (i = 1,2; allgemein: 1=1,…, r)
Merkmal B: Art der Ausbildung HTL, FH, UNI (j = 1,2,3; allgemein: j=1,…, s)
Die Frage lautet, ob die beiden Merkmal voneinander unabhängig sind oder nicht, m.a.W.: ist die
Eignung (für die ausgeschriebene) Stelle von der Art der Ingenieur-Ausbildung abhängig oder nicht
(mit einer Wahrscheinlichkeit von 95% bzw. bei einem Signifikanzniveau von 5%).
Kontingenztabelle:
HTL-Ingenieure
h
geeignet
ungeeignet
Spaltensumme
h
FH-Ingenieure
h
h
Diplomingenieure
h
Summe
h
14
16
10
25
16
19
40
60
30
35
35
100
Null- und Alternativhypothese
H0: die beiden Merkmal A und B sind voneinander unabhängig
H1: die beiden Merkmale A und B sind nicht voneinander unabhängig (sie sind abhängig
voneiander)
Prüfgröße
Zunächst sind die erwarteten absoluten Häufigkeiten zu berechnen: heij
Dazu sind die Spaltensummen im Verhältnis der Zeilensummen aufzuteilen.
© W. Blaas 2006
Vorlesung Inferenzstatistik
34
HTL-Ingenieure
geeignet
ungeeignet
Spaltensumme
FH-Ingenieure
Diplomingenieure
h
h
h
h
h
h
14
16
12
18
10
25
14
21
16
19
14
21
30
35
35
Zeilensumme
40
60
100
Sodann ist (analog zum CHiquadrat-Anpassungstest) die Prüfgröße
r
s
PG  
i 1 j 1
(hijb  hije ) 2
hije
zu berechnen, wobei
r
s
Anzahl der möglichen Ausprägungen des ersten Merkmals (A)
Anzahl der möglichen Ausprägungen des zweiten Merkmals (B)
bedeuten. Im vorliegenden Beispiel ist PG=2,937
Annahmebereich:
Die Nullhypothese ist auf dem Signifkanzniveau  anzunehmen, wenn die Prüfgröße kleiner als das
5%-Fraktil der Chiquadratverteilung mit f = (r-1)*(s-1) Freiheitsgraden ist
Dieser Fraktilwert ist CHIINV(; f) = 5,991
Ergebnis
Weil
² < CHIINV(; f)
nämlich 2,94 < 5,99
ist die Nullhypothese (auf dem Signifikanzniveau ) anzunehmen.
© W. Blaas 2006
Vorlesung Inferenzstatistik
35
Kapitel 7: Zusammenfassender Überblick
ZIEL
METHODE
Schätzen des Anteils
Schätzen von
Anteilswerten bei
Normalverteilung
mit Korrektur
ohne Korrektur
ANWENDUNGSBEDINGUNGEN
n  30
p > 0,1
n/N > 0,05
n/N  0,05
Ermittlung des
erforderlichen
Stichprobenumfanges
Schätzen des
Mittelwertes
Schätzen von
Anteilswerten bei
Nicht-Normalverteilung
n  30
p  0,1
Mittelwertschätzung
bei Normalverteilung
mit Korrektur
ohne Korrektur
n  30
n/N > 0,05
n/N  0,05
Ermittlung des
erforderlichen
Stichprobenumfanges
Testen von Hypothesen Sequentieller
über den Fehleranteil
Hypothesentest
Testen einer
Verteilungshypothese
Chiquadrat-Test
e
hi 5
ERFORDERLICHE
ANGABEN
Grundgesamtheit N
Stichprobenumfang n
Stichprobenergebnis p
Wahrscheinlichkeit w
Grundgesamtheit N
Genauigkeit e
Stichprobenergebnis p
Wahrscheinlichkeit w
Grundgesamtheit N
Stichprobenumfang n
Stichprobenergebnis p
Wahrscheinlichkeit w
Chiquadrat-Wert
Grundgesamtheit N
Stichprobenumfang n
Stichprobenmittelwert
Wahrscheinlichkeit w
Stichprobenvarianz
Grundgesamtheit N
Genauigkeit e
Wahrscheinlichkeit w
Stichprobenvarianz
Nullhypothese H0
Gegenhypothese H1
Auftraggeberrisiko 
Prüferrisiko 
b
e
hi, hi
Auftraggeberrisiko 
k
ERGEBNIS
REFERENZ
Konfidenzintervall
für den
Anteil
(mit Korrekturfaktor)
(ohne Korrekturfaktor)
Stichprobenumfang
(mit Korrekturfaktor)
(ohne Korrekturfaktor)
Kapitel 4
Obergrenze
für den
Fehleranteil bzw.
die Fehleranzahl
Kapitel 4
Konfidenzintervall
für den
Mittelwert
(mit Korrekturfaktor)
(ohne Korrekturfaktor)
Stichprobenumfang n
(mit Korrekturfaktor)
(ohne Korrekturfaktor)
Kapitel 5
Annahmezahl a und
Ablehnungszahl z
in Abhängigkeit von
Stichprobenumfang n
und den Eingabewerten
Annahme/Ablehung der
Verteilungs-Hypothese
Kapitel 6
Kapitel 4
Kapitel 5
Kapitel 6
Vorlesung Inferenzstatistik
36
8. Literaturhinweise
BLEYMÜLLER Josef et al., Statistik für Wirtschaftswissenschaftler. 10. Aufl., Verlag Franz
Vahlen, München 1996
BOHLEY, Peter, Statistik - Einführendes Lehrbuch für Wirtschafts- und Sozialwissenschaftler. 3.
Aufl., Oldenbourg. 1989
SACHS Lothar, Angewandte Statistik. Planung und Auswertung, Methoden und Modelle. SpringerVerlag, Berlin Heidelberg New York 1974
STENGER Horst, Stichproben. Physica-Verlag, Heidelberg Wien 1986
WETZEL Wolfgang et al., Statistische Tabellen. Verlag Walter de Gruyter, Berlin 1967
WYSOCKI Klaus v., Grundlagen des betriebswirtschaftlichen Prüfungswesens. 2. Auflage. Verlag
Vahlen, München 1977. Zitiert als "WYSOCKI [2]".
WYSOCKI Klaus v., Grundlagen des betriebswirtschaftlichen Prüfungswesens. 3. Auflage. Verlag
Vahlen, München 1988. Zitiert als "WYSOCKI [3]".
© W. Blaas 2006