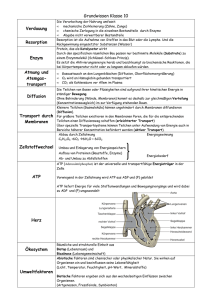
Die kinetische Energie der Moleküle

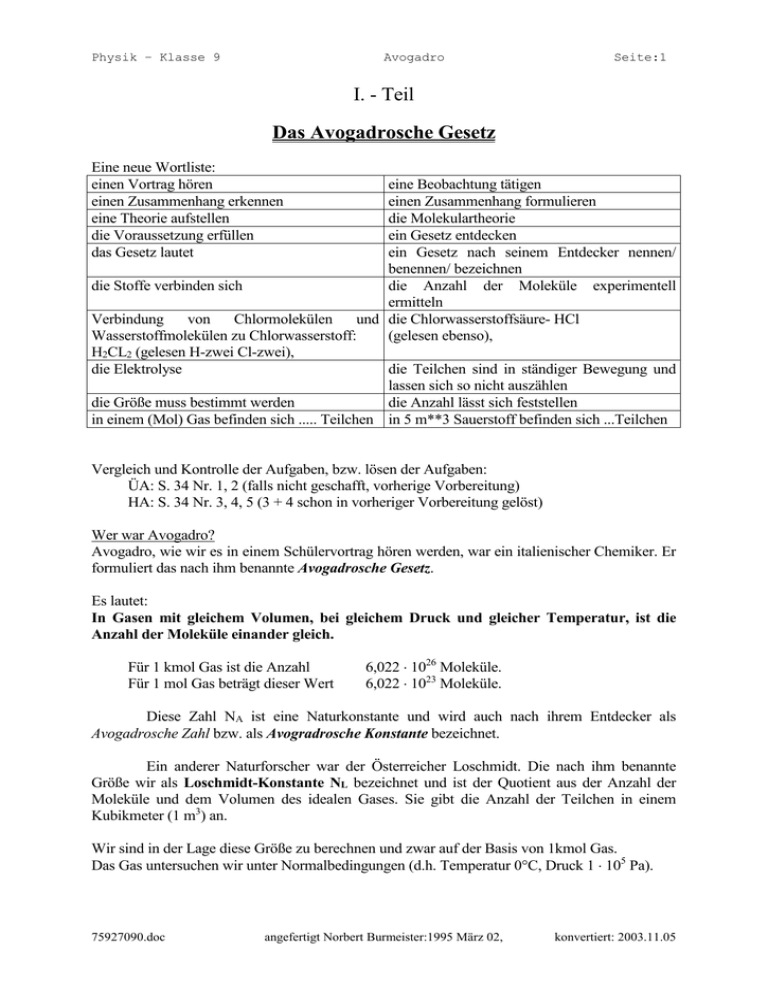
Physik – Klasse 9
Avogadro
Seite:1
I. - Teil
Das Avogadrosche Gesetz
Eine neue Wortliste:
einen Vortrag hören
einen Zusammenhang erkennen
eine Theorie aufstellen
die Voraussetzung erfüllen
das Gesetz lautet
eine Beobachtung tätigen
einen Zusammenhang formulieren
die Molekulartheorie
ein Gesetz entdecken
ein Gesetz nach seinem Entdecker nennen/
benennen/ bezeichnen
die Stoffe verbinden sich
die Anzahl der Moleküle experimentell
ermitteln
Verbindung
von
Chlormolekülen
und die Chlorwasserstoffsäure- HCl
Wasserstoffmolekülen zu Chlorwasserstoff:
(gelesen ebenso),
H2CL2 (gelesen H-zwei Cl-zwei),
die Elektrolyse
die Teilchen sind in ständiger Bewegung und
lassen sich so nicht auszählen
die Größe muss bestimmt werden
die Anzahl lässt sich feststellen
in einem (Mol) Gas befinden sich ..... Teilchen in 5 m**3 Sauerstoff befinden sich ...Teilchen
Vergleich und Kontrolle der Aufgaben, bzw. lösen der Aufgaben:
ÜA: S. 34 Nr. 1, 2 (falls nicht geschafft, vorherige Vorbereitung)
HA: S. 34 Nr. 3, 4, 5 (3 + 4 schon in vorheriger Vorbereitung gelöst)
Wer war Avogadro?
Avogadro, wie wir es in einem Schülervortrag hören werden, war ein italienischer Chemiker. Er
formuliert das nach ihm benannte Avogadrosche Gesetz.
Es lautet:
In Gasen mit gleichem Volumen, bei gleichem Druck und gleicher Temperatur, ist die
Anzahl der Moleküle einander gleich.
Für 1 kmol Gas ist die Anzahl
Für 1 mol Gas beträgt dieser Wert
6,022  1026 Moleküle.
6,022  1023 Moleküle.
Diese Zahl NA ist eine Naturkonstante und wird auch nach ihrem Entdecker als
Avogadrosche Zahl bzw. als Avogradrosche Konstante bezeichnet.
Ein anderer Naturforscher war der Österreicher Loschmidt. Die nach ihm benannte
Größe wir als Loschmidt-Konstante NL bezeichnet und ist der Quotient aus der Anzahl der
Moleküle und dem Volumen des idealen Gases. Sie gibt die Anzahl der Teilchen in einem
Kubikmeter (1 m3) an.
Wir sind in der Lage diese Größe zu berechnen und zwar auf der Basis von 1kmol Gas.
Das Gas untersuchen wir unter Normalbedingungen (d.h. Temperatur 0C, Druck 1  105 Pa).
75927090.doc
angefertigt Norbert Burmeister:1995 März 02,
konvertiert: 2003.11.05
Physik – Klasse 9
NL 
Avogadro
Seite:2
N A 6,022 10 26
1

 2,68 10 25 3
3
VN
22,4m
m
Wir wollen den Stoff festigen und wiederholen deshalb:
Frage: Welche Kenntnisse besitzen wir über die Anzahl der Moleküle?
Welche Energie besitzt ein kmol ideales Gas und wie lautet die Formel zu ihrer
Berechnung?
Wodurch unterscheiden sich die Avogadrosche Konstante und die Lochschmidt
Konstante?
II. - Teil
Die kinetische Energie der Moleküle
Bestimmen wir die Energie eines Moleküls im idealen Gas:
Wir stellen folgende Betrachtung an:
Uns ist sowohl die kinetische Energie als auch die Anzahl der Teilchen für 1 kmol Gas
bekannt. Aus diesem Zusammenhang erkennen wir, dass wir die schon berechnete Energie für
1kmol Gas nur noch durch die Anzahl der vorkommenden Teilchen zu dividieren brauchen, um
die kinetische Energie eines einzelnen Moleküls zu bestimmen.
E kin 
3  p  V 3360000 J

 5,6 10 21 J
26
2 N A
6 10
Einige wichtige Bemerkungen:
Die kinetische Energie ist für die Moleküle aller Gase gleich. Die Moleküle
verschiedener Gase besitzen unterschiedliche Massen. Daraus ergibt sich, dass die Teilchen mit
kleinerer Masse schneller sind, als die mit größerer.
Wir schlussfolgern, dass Moleküle mit kleiner Masse schneller diffundieren, d.h. Gase
breiten sich mit verschiedenen Geschwindigkeiten aus und die leichteren Gase sind schneller.
Betrachtungen zu Masse und Anzahl:
Berechne die Masse bzw. die Anzahl der Teilchen, wo es sich nicht um die
Normgrößen handelt. Weiterhin wenden wir auf diesen Zustand das Boyle-Mariottesche Gesetz
an.
HA: S.38 Nr. 3;
S.39 Nr. 3, 4
Vorbereitender Schülervortrag: Kelvin, Celsius
ÜA: S.38 Nr. 1, 2; S.39 Nr. 1, 2
Allgemeine Auflösung:
75927090.doc
angefertigt Norbert Burmeister:1995 März 02,
konvertiert: 2003.11.05
Physik – Klasse 9
Avogadro
Seite:3
 Die Anzahl der Moleküle einer bestimmten Molmenge ist konstant: 1kmol = 61026
Avogadrosche Zahl,
3  p V
 Die Energiemenge und die Formel zu ihrer Berechnung lautet:
 3360000 J
2
S.38 Nr. 1
Geg.: H2 Wasserstoffmolekül,
M = 2Kg je kmol
NA = 6  1026 Moleküle je kmol
ges.: m je Molekül
Lösung:
2kg
M

 3,667 10  27 kg  3,667 10  24 g
26
N A 6 10
Ein Wasserstoffmolekül hat die Masse von 3,667  10-27 kg
m
S.38 Nr. 2
Geg.: VLu = 1 dm3 Luft
ges.: NLu
3
1 mol  29 g  V = 22,4 dm  NA = 6  1023
Lösung:
Wir stellen ein Verhältnis auf:
N A : V N  N Lu : V Lu umgestellt nach N Lu
N A  V Lu 6 10 23 1dm 3
N Lu 

 2,68 10 22
3
VN
22,4dm
3
In 1 dm Luft sind 2,68  1022 Teilchen Gas enthalten. Dies entspricht der Lochschmidt
Konstante für 1 dm3.
S. 38 Nr. 3
Geg.: VEl = 80 cm3 = 0,08 dm3
ges.: NEl
1 mol  29 g  V = 22,4 dm3  NA = 6  1023
Lösung:
N A : V N  N El : V El
N El
damit ist
N A  V El 6 10 23  0,08dm 3


 2,14 10 22
3
VN
22,4dm
N ER 
N El
9
 2,14 1013
10
In der Elektronenröhre sind 2,14  1013 Teilchen enthalten.
S. 39 Nr. 1
Geg.: v = 629 m/s
E = 3 360 000 J / 6  1026 = 5,6  10-21 J
ges.: m
Lösung:
75927090.doc
angefertigt Norbert Burmeister:1995 März 02,
konvertiert: 2003.11.05
Physik – Klasse 9
Avogadro
Seite:4
m  v2

2
2 E 11,2  10  21 J
m 2 
 2,83  10  26 kg
m
v
(629 ) 2
s
Die Masse dieses Gasteilchens beträgt 2,83  10-26
E
S.39 Nr. 2
Geg.: V2 = 6 dm3
ges.: N
1 mol  29 g  VN = 22,4 dm3  NA = 6  1023
p2 = 25 N/cm˛ = 2,5  105 Pa
p1 = 1  105 Pa
Lösung:
a) Boyle- Mariotte
p1  V1  p 2  V2 dann ist
V1 
p 2  V2 2,5  10 5 Pa  6dm 3

 15dm 3
5
p1
1  10 Pa
b) Teilchenzahl
N A : V N  n1 : V1  6  10 23  22,4dm 3  n1 : 15dm 3
6  10 23  15dm 3
n1 
 4,017  10 23
3
22,4dm
Im Gefäß befinden sich 4,017 1023 Teilchen.
S.39 Nr. 3
Geg.: v = 499 m/s
p = 8 N/cm˛ = 0,8  105 Pa
Lösung:
3p
v

ges.:ρ


3 p 3  0,8  10 5 Pa
kg
g

 9,63 3  9,63 3
2
2
v
m
dm
m

 499 
s

Die Dichte des Gefäßes beträgt bei diesem Druck 9,63 kg/m3
S. 39 Nr. 4
Geg.: V1 = 1 cm3
VN = 22,4 cm3
NA = 6  1020
75927090.doc
ges.: N1 und N1/6
N19
angefertigt Norbert Burmeister:1995 März 02,
konvertiert: 2003.11.05
Physik – Klasse 9
Avogadro
Seite:5
Lösung:
V1 V N
=
, wird nach N 1 umgestellt.
N1 N A
28
3
N A  V 1 6  10  1 cm
=
=
= 2,68  1019 Teilchen sind im gesamten Gefäß.
N1
3
22,4 cm
VN
Für eine Seite des Würfels gilt damit
19
N1
10
= 2,68 
= 4,46  1018
6
6
4,46  1018 Teilchen üben auf eine Seite des Würfels einen Druck aus.
Nach Boyle-Mariotte können wir jetzt feststellen, dass p1  V1 = p2  V2, da sich hier aber
nicht das Volumen, sondern die Masse verändert, ===> p1 = 1/ 1019 p2
Das bedeutet andersherum:
p1 V 2
=
p2 V 1
da mit dem konstanten Volumen sich nur der Druck ändert, wenn wir die Masse
ändern, bedeutet dies für uns, dass sich damit die Dichte ändert.
m2
2
m1
1
p1  1
=
p2  2
=
75927090.doc
Mit anderen Worten: Das Verhältnis der Drücke zueinander verhält sich wie das
Verhältnis ihre Dichten. Wir beachten, dass eine direkte Proportionalität herrscht.
Die Drücke verhalten sich proportional zu ihren Dichten.
angefertigt Norbert Burmeister:1995 März 02,
konvertiert: 2003.11.05