VWL-Hausaufgaben
Werbung

VWL-Hausaufgaben Mikro Frage 1 a) Erläutern Sie ausführlich, was man unter "freien Gütern" und was man unter "knappen Gütern" versteht. Die Güter in der VWL teilen sich auf in knappe und freie Güter. Freie Güter sind für jedermann kostenlos und in ausreichender Menge vorhanden (z.B. Luft zum Atmen). Sie unterliegen keinen irgendwie gearteten Beschränkungen. Sie sind In beliebiger Menge verfügbar, deshalb gibt es für sie auch keinen Preis. Theoretisch gesehen würden sich Angebots- und Nachfragefunktion nicht schneiden. xNmax < xAmin Ein Gut wird als knapp angesehen, wenn es selten und nützlich ist. Es bestehen folglich Beschränkungen bzgl. der Menge, was zur Folge hat, dass nicht jeder seine Bedürfnisse an einem bestimmten Gut ausreichend befriedigen kann. Diese Nachfrage nach knappen Gütern regelt dann den Wert. Je knapper etwas ist, desto begehrter ist es und desto höher ist der Wert anzusehen. Weiterhin bestehen oftmals starke regionale Unterschiede im Vorhandensein eines Gutes und dieses kann zusätzlich zeitlichen Veränderungen unterworfen sein (z.B. Öl). b) Trinkwasser ist lebenswichtig, also sehr nützlich. Erläutern Sie, unter welchen Umständen es ein freies Gut ist und unter welchen Umständen es als ein "ökonomisches Gut" angesehen werden muß. Trinkwasser muß heutzutage in unserer Region als knappes Gut angesehen werden, da es nicht in ausreichender Menge jedem erreichbar zur Verfügung steht. Wir bezahlen für das Sachgut Trinkwasser als Unterkategorie der „Ökonomischen“, also knappen Güter. In Gegenden, in denen Trinkwasser z.B. als natürliches, für jeden kostenfrei zugängliches Quellwasser vorhanden ist, kann es jedoch als freies Gut angesehen werden. c) Unter welchen Umständen wären zB Gartenzwerge ein freies Gut, unter welchen anderen Umständen sind sie ein ökonomisches Gut? Angenommen, Gartenzwerge würden an Bäumen wachsen, dann wären sie ein freies Gut, da sie jedoch hergestellt werden, stecken in ihnen Wirtschaftsfaktoren, die eine Gegenleistung erfordern. U f ´1 x1dumm! Die Frage ist mir zu dumm! Oder ich bin zu f ´1 0 Frage 2 a) Erläutern Sie die Ober-Begriffe "Wirtschaftssubjekt" , "Wirtschaftsobjekt" und "Wirtschaftliche Transaktion". Nennen Sie weitere wichtige Unterteilungen für Wirtschaftssubjekte, für Wirtschaftsobjekte und für wirtschaftliche Transaktionen und geben sie jeweils ein praktisches Beispiel. Als Wirtschaftssubjekt wird jede selbständig handelnde Einheit einer Volkswirtschaft bezeichnet. Ein Wirtschaftssubjekt ist die natürliche oder juristische Person, die im Wirtschaftsleben agiert und handelt. Sie wirtschaftet mit Waren oder Dienstleistungen, hat die Möglichkeit aktiv ins Geschehen einzugreifen. Als Wirtschaftsobjekte sollen alle materiellen Dinge, immatrielle Leistungen und mit besonderen Rechten ausgestatteten Positionen heißen, um die sich wirtschaftliches Handeln dreht. Mann kann den Begriff Wirtschaftsobjekt auch durch den Begriff „Gut“ ersetzen. Volkswirte reduzieren die Handlungen von Menschen und Organisationen auf wirtschaftlich relevante Handlungen und nennen sie Transaktionen. Aufgrund der Arbeitsteilung, die sich im Laufe der Entwicklungsgeschichte der Menschheit herausbildete, kommt kein Wirtschaftssubjekt ohne Interaktionen mit anderen Wirtschaftssubjekten aus. Volkswirte nennen diese Handlungen Transaktionen, weil Ressourcen von einem Wirtschaftssubjekt zum anderen fließen. Beim Übergang der Objekte entstehen Forderungen. Der Inhaber einer solchen Forderung wird Gläubiger genannt. Er hat den Anspruch gegen den Schuldner. Hier herrschen also Kreditbeziehungen zwischen den einzelnen Wirtschaftssubjekten. Es entstehen Forderungen und Verbindlichkeiten. Da eine Transaktion entweder im Tausch gegen ein anderes Gut, eine andere Forderung oder ohne Gegenleistung geschehen kann, gibt es insgesamt 5 Arten ökonomischer Transaktion: 1.. Tausch Gut gegen Gut: Realtausch (auch Natural- oder Gütertausch genannt) 2.. Übertragung (auch Transfer) eines Gutes. = Übergang ohne Gegenleistung, heißt auch Schenkung oder Realtransfer 3.. Tausch Gut gegen Forderung: Hauptsächlich Kauf bzw. Verkauf 4.. Übertragung einer Forderung ohne Gegenleistung: Schenkung oder Forderungstransfer. Die Übertragung von Geld nennt man auch Transferzahlung 5.. Tausch Forderung gegen Forderung: Hauptsächlich Kauf bzw. Verkauf b) Was versteht man unter menschlichen Bedürfnissen, wie lassen sie sich untergliedern? Bedürfnis, in der Wirtschaftstheorie verwendeter Begriff für ein subjektives Empfinden des Mangels aufseiten der Nachfrager, den es durch ein entsprechendes Angebot zu decken gilt. Unterschieden werden dabei existentielle Bedürfnisse oder Grundbedürfnisse (Nahrung, Kleidung, Wohnung, Bildung u. ä. m.), Wohlfahrts-, Luxus- und Prestigebedürfnisse sowie individuelle und kollektive Bedürfnisse. In der Theorie der Marktwirtschaft wird die Produktion im Grunde von den Bedürfnissen der Wirtschaftssubjekte bestimmt; in Wirklichkeit erzeugen aber die Produzenten durch die Bereitstellung bzw. Inaussichtstellung bestimmter Güter beim Konsumenten häufig erst ein Bedürfnis. In der Psychologie sind die durch unbefriedigte Bedürfnisse verursachten psychischen Spannungen (Bedürfnisspannung) die eigentliche Triebfeder menschlichen Handelns. Unterschieden wird hier zwischen primären, angeborenen Bedürfnissen (Trieb- oder Vitalbedürfnisse) wie Hunger, Durst und Schutz vor Gefahr sowie sekundären, erworbenen Bedürfnissen, z. B. die geistig-kulturellen Interessen des Menschen. c) Was bedeutet es für die Bedürfnisbefriedigung, wenn es knappe Güter gibt? Die menschlichen Bedürfnisse auf knappe Güter rufen ein Optimierungsproblem hervor: Gibt es knappe Güter, besteht die Frage nach der Aufteilung. Wer bekommt etwas von den nicht in ausreichender Menge vorhandenen Dingen. Wie viel bekommt ein jeder der in Frage kommenden? d) Welche Möglichkeiten kennen Sie, das Problem der Verteilung knapper Güter praktisch zu lösen? (Mindestens 5 Alternativen) 1) 2) 3) 4) 5) Zentrale Verteilung nach schwere des Mangels Selbstregelung durch den Preis Steigerung der Produktion dieser knappen Güter … … c) Welche wichtigen ökonomischen Entscheidungen trifft ein privater Haushalt (HH) , welche wichtigen ökonomischen Entscheidungen triff ein Produktionsunternehmen? Der private HH entscheidet darüber, welche verschiedenen Gütern (Sachgütern und Dienstleistungen) für das Funktionieren des HH erforderlich sind (Nachfrage). Der Produktionsunternehmer hingegen entscheidet darüber, welche und wie viele Güter er anbietet und welche Produktionsfaktoren er für die Herstellung einsetzen muss (Angebot). d) Erläutern Sie die drei Stufen einer rationalen Entscheidung über ökonomische Güter (knappe Resourcen). „Drei-Schritt-Lehre“ (Zweck)Rationales-Handeln) Diese Theorie beschreibt die Untersuchung von Alternativen und die Entscheidungsfindung eines Wirtschaftssubjektes in Fragen knapper Güter: 1) Alternativen untersuchen (Voraugenführen der Möglichen Alternativen / Untersuchen nach Unterschieden und Gemeinsamkeiten) 2) Alternativen (subjektiv) bewerten (Vor- und Nachteile werden sich vor Augen geführt / Dies 3) unterliegt subjektiven Gesichtspunkten) Beste Alternative auswählen (Das WS wählt die für sich am besten geeignete Alternative aus) Frage 3 a) Welches sind die beiden großen Teilgebiete der Volkswirtschaftslehre? Beschreiben Sie die Unterschiede der Betrachtungsperspektive, des Aggregationsgrades und erläutern Sie die jeweiligen Aufgabenfelder. Die Mikroökonomik ist dasjenige Teilgebiet der Wirtschaftswissenschaft, das das Verhalten kleiner Wirtschaftseinheiten untersucht, z. B. einzelner Haushalte und Unternehmen, und davon ausgehend wirtschaftliche Tatbestände erklärt. Für die Mikroökonomik ist die Nachfrage das Ergebnis von Plänen der Haushalte, das Angebot das Ergebnis der Pläne von Unternehmen. Die Mikroökonomik geht davon aus, dass Verbraucher und Produzenten sich rational verhalten und nach dem ökonomischen Prinzip wirtschaften: Sie wollen mit gegebenen Mitteln einen möglichst großen Nutzen erzielen (Maximumprinzip) oder ein vorgegebenes Ziel mit möglichst wenig Aufwand erreichen (Minimumprinzip). Haushalte fragen sich beispielsweise, wie sie mit einem gegebenen Einkommen möglichst viele Konsumgüter kaufen können. Unternehmen fragen sich, wie sie einen festgesetzten Produktionsausstoß (Output) am kostengünstigsten produzieren (Minimumprinzip, Gewinnmaximierung). In der Makroökonomik hingegen wird die Entwicklung der Globalgrößen im gesamtwirtschaftlichen Kreislauf untersucht, d. h. den Zusammenhang zwischen Wachstum des Volkseinkommens, Beschäftigung, Investition, Konsum, Sparen und Preisniveau. Die Makroökonomik erhält die Globalgrößen, indem sie mikroökonomische Größen zusammenfasst (Aggregieren), z. B. die Konsumausgaben aller Haushalte zu Gesamtkonsum, die Ersparnisse aller Haushalte zu Gesamtersparnis, die Investitionen aller Unternehmen zu Gesamtinvestition. Zwischen den Globalgrößen bestehen folgende Zusammenhänge: Das Volkseinkommen wächst mit dem Beschäftigungsstand, dessen Ausmaß wiederum von der Nachfrage nach Konsum- und Investitionsgütern abhängt. Die Nachfrage nach Konsumgütern hängt von der Höhe der Einkommen ab. Die Nachfrage nach Investitionsgütern (Maschinen etc.) hängt davon ab, wie hoch der aus den Investitionsgütern erwartete Gewinn im Vergleich zu den Zinsen ist, die für Ersparnisse gezahlt werden. Die Makroökonomik bildet die Grundlage für die volkswirtschaftliche Gesamtrechnung. In ihr werden für vergangene Perioden alle Güter- und Geldbewegungen zwischen den Wirtschaftssubjekten einer Volkswirtschaft (Haushalte, Unternehmen etc.) dargestellt und damit ein Gesamtbild des Wirtschaftsprozesses gezeigt. b) Ordnen Sie die folgenden Themen den obigen Teilgebieten zu: Mikroökonomik: -Familienentscheidung über die Höhe der Ersparnis aus dem Einkommen -Unternehmensentscheidung, wegen eines Kostenanstiegs Arbeitskräfte zu entlassen. -Wirkung einer Preiserhöhung des HVV auf seine Passagierzahlen und seine Erlöse Makroökonomik: -Wirkung erhöhter Ersparnisbildung auf das Wachstum des Sozialproduktes -Wirkungen einer Erhöhung der Tabaksteuer auf die Nachfrage nach Zigaretten und auf das Tabaksteueraufkommen. -Zusammenhang zwischen Geldmengenänderung und durchschnittlicher Inflationsrate Frage 4 a) Erläutern Sie die Unterschiede zwischen ökonomischer Beschreibung, Erklärung, Prognose und Beratung. Die Beschreibung steht immer an erster Stelle. Per Expost-Analyse werden hier die Verhältnismäßigkeiten erklärt: Die ex-post Analyse wird auch volkswirtschaftliches Rechnungswesen genannt. Hier werden quantitative Angaben über gesamtwirtschaftliche Größen ermittelt, wobei sich die Angaben auf die Vergangenheit beziehen. Sie dienen als quantitative Information für die Wirtschaftspolitik, und wird für den internationalen Vergleich mit anderen Nationen gebraucht. Mit ihr kann man die Leistungsfähigkeit der Volkswirtschaften vergleichen. Nach der Beschreibung folgt die Erklärung. Hier wird eine Kausalität behauptet und Modelle eingesetzt, um Sachverhalte abstrakter darzustellen. (Zu Modellen später mehr.) Die Prognose ist dann sozusagen das Derivat aus den Modellen. Was lässt sich erkennen, welche Ableitungen kann man treffen. Am Schluss steht dann die Beratung, also das Weitergeben der Erkenntnisse aus der Modell-Ableitung. Die letzten drei Begriffe gehören zur Ex-AnteAnalyse: Die ex-ante Analyse wird auch makroökonomische Theorie genannt. Ziel dieser ist es, zu klären, welche Determinanten in welcher Weise die Entwicklung gesamtwirtschaftlicher Größen beeinflussen und welche Wirkungszusammenhänge zwischen den gesamtwirtschaftlichen Größen bestehen. Sind die Probleme hinreichend geklärt, dann können mit Hilfe der makroökonomischen Theorie die Ergebnisse der ex-post Analyse ursächlich erklärt werden und die Entwicklung gesamtwirtschaftlicher Größen kann prognostiziert werden. b) K. Popper hat behauptet, daß eine Theorie die Wissenschaft nur dann weiterbringt, wenn sie im Prinzip durch eine empirische, datenorientierte Untersuchung widerlegt (falsifiziert) werden kann. Erklären Sie, warum eine Theorie, die nicht falsifiziert werden kann, keine gute Theorie ist. Falsifizierbarkeit ist im kritischen Rationalismus die Eigenschaft einer Hypothese oder Theorie, empirisch widerlegbar zu sein. Karl Popper geht von einer Asymmetrie universeller Hypothesen aus, z. B. „Alle Schwäne sind weiß”, wodurch die Möglichkeit nicht weißer Schwäne ausgeschlossen wird. Tritt in Form eines nicht weißen Schwans ein gegensätzlicher Fall auf, ist diese universelle Hypothese ungültig. Die Feststellung gleicher Fälle kann diese Hypothese jedoch nicht für immer bestätigen, da konträre Fälle in Zukunft nicht ausgeschlossen werden können. Demnach ist eine universelle Hypothese zwar endgültig falsifizierbar, aber nicht verifizierbar. Zeigen sich bei der Überprüfung (z. B. durch Experimente, Tests) nur gleiche Fälle, ist eine Hypothese trotzdem nur vorläufig bestätigt. Wohingegen sie beim Auftreten gegensätzlicher Fälle als endgültig gescheitert gilt. c) Erläutern Sie den Unterschied zwischen einer positiven und einer normativen ökonomischen Analyse an folgenden Beispielen: Wirkungsanalyse einer Benzinsteuersenkung auf die Automobilnachfrage/ Wirkung auf das Benzin-Steueraufkommen/ Wirkung auf die Verschuldung des Staatshaushaltes/ Ist eine Benzinsteuersenkung wünschenswert?/ Wie hoch sollte die Benzinsteuer sein?. (Vgl. dazu etwa Pindyck/Rubinfeld Kap.1.1.2 ) b) Wenn Sie Bundeskanzler/in wären, würden Sie sich mehr für die positiven oder für die normativen Aussagen Ihrer Wirtschaftsberater interessieren? (mit Begründung). Frage 5 a ) Erläutern Sie Bedeutung von Modellen für die ökonomische Erkenntnis. Was ist von der Kritik zu halten, ein Modell würde die Wirklichkeit nicht zu 100 % korrekt abbilden? In der Alltags- und Wissenschaftssprache ist das Modell ein Objekt, das durch eine Struktur-, Funktions- oder Verhaltensanalogie zu einem Original erlaubt, dieses in schematisierter, auf wesentliche Züge komprimierter Darstellung wiederzugeben. Modelle sind Instrumente, um sehr komplexe wirtschaftswissenschaftliche Systeme zu vereinfachen und verständlich zu machen. Es sind meist nicht alle Einflüsse und Größen nötig, um etwas über einen Zusammenhang zu erfahren. Zusätzlich wären mit Informationen überladene Modelle viel zu undurchsichtig. Es wird also absichtlich großen Wert auf strukturierte Einfachheit gelegt. Unter Modellen versteht die VWL ein abstraktes Erkenntnisinstrument, das aber so einfach wie möglich ist und eine gewisse Geeignetheit aufweist. unabhängige Variable exogen Modell abhängige Variable endogen Zum Beispiel: Der Preis bestimmt die mengenmäßige Güternachfrage nach Bier. Preis Modell mengenmäßige Güternachfrage nach Bier Es geht aber auch anders herum, das die Summe der mengenmäßigen Nachfrage nach Bier den Preis bestimmt. Summe der mengenmäßigen Nachfrage nach Bier Modell Preis b) Was versteht man unter einer modell-exogenen Variable, was unter einer modellendogenen Variable? Bei welchen Fragestellungen ist z.b der Bierpreis eine exogene Variable (erklärende Variable), bei welcher Fragestellung eine endogene Variable(zu erklärende Variable)? Die „exogenen Variablen“ sind die Ursachen einer volkswirtschaftlichen Fragestellung. Bringt man diese in das sog. ökonomische Modell ein, erhält man daraus die endogenen Variablen, welche die Wirkung der Ursachen verdeutlichen. Exogene Variable endogene Variable Modell Erklärende V. zu erklärende V. Bei der Frage nach einem theoretischen Rückgang der Verkaufszahlen ist der Bierpreis eine erklärende (exogene) Variable. Bei der Frage nach einem Anstieg der Bierpreise, ist der Preis die zu erklärende (endogene) Variable, die dann z.B. mit einer schlechten Hopfenernte als erklärende Variable dargestellt werden kann. c) Warum wird das Wetter normalerweise in ökonomischen Modellen allenfalls als exogene Variable berücksichtigt? Was könnte ein Klimaforscher dazu kritisch anmerken? Wetter Prod. Prozeß Landwirtschaftliche Produktion Der Grund hierfür liegt natürlich darin, dass kurzfristig nichts das Wetter zu beeinflussen vermag. Die Klimaforscher hingegen bemerken schon seit langem, dass wir sehr wohl durch Treibhausgase etc. Einfluss auf das Klima und somit das Wetter nehmen, wenn auch auf längere Sicht. c) Nach einer statistische Untersuchung gibt es einen Zusammenhang zwischen der Anzahl der Feuerzeuge in Haushalten und der Krebswahrscheinlichkeit der dort lebenden Personen. Diskutieren Sie den kausalen Schluß, Feuerzeuge sollten wegen ihrer Gesundheitsgefährdung verboten werden. (Ausgelassene Variablen) Es lässt sich vielleicht nicht bestreiten, das es „statistisch“ gesehen wahr ist, jedoch muss bei der Erstellung von Modellen die Ursache in Verbindung zur Wirkung stehen, man muss also den Zusammenhang zwischen der Ursache und der Wirkung untersuchen / finden. In diesem Fall ist es höchst unwahrscheinlich, dass die im HH befindlichen Feuerzeuge die Krebswahrscheinlichkeit der dort lebenden Personen erhöht. d) Warum kann bei ökonomischem Verhalten die Wirkung u. U. früher zu beobachten sein als die eigentliche Ursache dieses Verhaltens? (Diskussion und Beispiel) Frage 6 a) Erläutern Sie die wichtigsten Unterschiede zwischen einer Zentralplanwirtschaft und einer Marktwirtschaft (Organisationsdiagramm). (Vgl. etwa: W. Cezanne, 2.Kapitel: Marktwirtschaft versus Planwirtschaft) Die Planwirtschaft ist eine Wirtschaftsordnung, in der das gesamte ökonomische Geschehen von einer zentralen Organisation nach einem von ihr festgelegten, einheitlichen Plan geleitet und gelenkt wird. Der Begriff „Planwirtschaft” erweckt den Eindruck, dass die Wirtschaft anderer Ordnungen nicht auf Plänen beruht, was faktisch natürlich falsch ist. Deshalb wird die „Planwirtschaft” in der Fachliteratur auch als „Zentralverwaltungswirtschaft” oder „zentral geleitete Wirtschaft” bezeichnet. Da sich die Nachfrage der Verbraucher nach Waren und Dienstleistungen in einer zentral geleiteten Wirtschaft nicht verbindlich festlegen, sondern immer nur abschätzen lässt, entstehen zahlreiche Schwierigkeiten. Typische Beispiele für diese Wirtschaftsordnung sind die Volkswirtschaften der ehemaligen sozialistischen Länder Osteuropas, wie z. B. die der Sowjetunion oder der DDR. Wesentliches Merkmal deren Wirtschaft waren die Vergesellschaftung der Produktionsmittel, die zentrale Planung des Wirtschaftsprozesses, die administrative Festlegung von Preisen und Löhnen und ein staatliches Außenhandelsmonopol. Im Gegensatz zur Zentralverwaltungswirtschaft steht die freie Marktwirtschaft, bei der die freien Kräfte des Marktes, Angebot und Nachfrage, Produktion und Verteilung der Waren und Dienstleistungen bestimmen. Bei der Einordnung der zentral geleiteten Wirtschaft ist zu bedenken, dass es in der wirtschaftlichen Praxis kaum beide Wirtschaftssysteme in Reinkultur gegeben hat. So kann auch eine Zentralverwaltungswirtschaft in Teilbereichen Elemente einer Marktwirtschaft enthalten, sind in allen Marktwirtschaften heute Teilbereiche zu finden, in denen der Staat mehr oder weniger stark eingreift und damit ganz oder teilweise das freie Spiel des Marktes wieder aufhebt. Die entsprechenden Interventionsformen werden auch als Dirigismus bezeichnet. Unternehmen Planvorschriften Planbehörde Planvorschriften = Transaktionen Abb.: Organisationsdiagramm einer Zentralwirtschaft Haushalte Konsumgütermärkte Einnahmen Ausgaben güter Konsum- Unternehmen Haushalte leistungen Faktor- Kosten Faktormärkte Einkommen Abb.: Güter – und Geldkreislauf in der Marktwirtschaft b) Nehmen Sie an, Sie seien als Chef der Planungsbehörde in einer Zentralplanwirtschaft für die Produktion von PKW´s im Lande verantwortlich. Welche Informationen benötigen Sie, um Ihre Aufgabe zu erfüllen? Ich benötige Informationen über: Erreichbarkeit, Verfügbarkeit und Preis von Produktionsfaktoren / Benötigte Menge an PKW´s / Erzielbarer Preis bei Verkauf der Wagen usw. usw. c) Wie wird demgegenüber die Produktion von PKW´s in einer Marktwirtschaft bestimmt? Warum gibt es in einer Marktwirtschaft kein Chaos, obwohl viele Millionen Wirtschaftssubjekte ihr ökonomisches Verhalten autonom planen und nicht miteinander abstimmen. Die Marktwirtschaft regelt sich im besten aller Fälle von selbst durch Nachfrage und Preis. Es wird nichts festgesetzt, sondern ergibt sich aus dem Zusammenspiel aller Wirtschaftsfaktoren. d) Was versteht man unter einem Konkurrenzmarkt? Unter einem Konkurrenzmarkt (auch Wettbewerbsmarkt) versteht man einen Markt mit einer großen Anzahl von Anbietern und Nachfragern, die identische Güter handeln. Der einzelne Marktteilnehmer hat dadurch einen äußerst kleinen Einfluss auf den Marktpreis und wird somit zum Preisnehmer bzw. Mengenanpasser. Vielmehr ist ihm sein Einfluss dabei sogar unbekannt. e) Durch welche ökonomischen Größen wird die nachgefragte Gütermenge eines privaten HH beeinflußt? - Nutzen maximieren - Einkommen - Bedürfnisse f) Durch welche ökonomischen Größen wird die Angebotsgütermenge eines Unternehmens beeinflußt? - Gewinn maximieren - Faktormenge (z.B. Arbeit, knappe Güter) Frage 7 a) Zeigen Sie mit drei selbstgewählten Alternativen mit einem Zeitbedarf von jeweils 4 Stunden , wie ein HWI-Student über die Verwendung seiner knappe Zeit (begrenztes Zeitbudget) Freitags von 12 bis 16 Uhr rational entscheiden kann. Erläutern Sie die drei Stufen seiner Entscheidung. Da Zeit bekanntlich ein knappes Gut ist, kommt hier die „Drei-Schritt-Lehre“ Anwendung: zur 4) Alternativen untersuchen (Voraugenführen der Möglichen Alternativen / Untersuchen nach Unterschieden und Gemeinsamkeiten) - Vorlesung bei Berry White Langsam aufstehen und bei McD das fettige Burger-Frühstück reinziehen, nach dem mein Körper nach dieser Nacht auf dem Kiez jetzt schreit Im Stadtpark Kicken und grillen 5) Alternativen (subjektiv) bewerten (Vor- und Nachteile werden sich vor Augen geführt / Dies unterliegt subjektiven Gesichtspunkten) … 6) Beste Alternative auswählen (Das WS wählt die für sich am besten geeignete Alternative aus) … b) Warum spricht man hier von Zweck-Rationalität? Das Individuum fällt eine möglichst rationale Entscheidung, da es sich Vor- und Nachteile der einzelnen Varianten gegenüberstellt und diese dann abwägt. Die Rationalität erfolgt zum Zweck der möglichst richtigen Entscheidung bei einem vorliegenden Problem. c) In einer anderen Knappheitssituation muß/darf der HWI-Student über die Verwendung von 100 Euro entscheiden. Erläutern Sie auch diese Entscheidung. … bla bla bla Frage 8 Auch auf gesamtwirtschaftlicher Ebene muß über knappe Güter entschieden werden : a) "Airbus oder Äpfel": Startbahnverlängerung oder Neuenfelder Apfelanbau. b) "Kanonen oder Butter":Produktionsentscheidung eines Landes im Krieg Erläutern Sie die Knappheitssituation und die drei Stufen der Entscheidungsfindung. … bla bla bla Immer das selbe! Frage 9 Was versteht man unter einem "Markt" (Geben Sie Beispiele), was geschieht auf einem Markt, wie läßt sich ein Markt abgrenzen? Was versteht man unter einem "Vollständigen Wettbewerbsmarkt" und unter dem "law of one price" für einen Markt? (Vgl. etwa Pindyck/Rubinfeld Kap. 1) Der Markt (von lateinisch mercatus: Handel, Messe) ist im engeren Sinne ein Ort, an dem sich Käufer und Verkäufer treffen, um wirtschaftliche Güter gegen Geld zu tauschen. Im weiteren Sinne ist ein Markt jedes Zusammentreffen von Angebot und Nachfrage, unabhängig davon, ob er geographisch oder zeitlich eindeutig bestimmbar ist, wie beispielsweise ein Wochenmarkt, oder ob er ein weltweiter Markt ist wie der Markt für Investitionsgüter (Maschinen u. a.). Auch ist es gleichgültig, unter welchen Umständen Angebot und Nachfrage zusammentreffen. Beim Devisenmarkt beispielsweise einigen sich Käufer und Verkäufer am Telefon. In der klassischen volkswirtschaftlichen Theorie bildet sich als Ergebnis des Zusammenwirkens von Angebot und Nachfrage der Marktpreis: Er ist ein Gleichgewichtspreis und liegt im Schnittpunkt zwischen Nachfrage- und Angebotskurve (bei den meisten wirtschaftlichen Gütern steigt die Nachfrage mit sinkendem Preis, während das Angebot mit dem Preis steigt). Zum Marktpreis kann die größtmögliche Gütermenge abgesetzt werden; er räumt den Markt, d. h., es gibt weder einen Angebots- noch einen Nachfrageüberhang. Der Marktpreis zeigt die Knappheit eines Gutes an: Je knapper das Angebot eines begehrten Gutes ist, desto eher kann man den Preis anheben, z. B. für Äpfel nach einem schlechten Erntejahr. Umgekehrt sinkt der Preis für ein Gut, wenn das Angebot größer ist als die Nachfrage. Der Marktpreis kann sich nur frei bilden, wenn auf einem Markt ein vollkommener Wettbewerb (=Vollständigen Wettbewerbsmarkt) herrscht: Keiner unter den Anbietern und Nachfragern darf so viel Macht haben, dass er den Preis beeinflussen kann. Der vollkommene Wettbewerb ist die theoretische Grundvoraussetzung für eine freie Marktwirtschaft. Realisiert wird solch ein vollkommener Markt in der Praxis am ehesten an der Börse. Reale Märkte sind dadurch gekennzeichnet, dass Unternehmen versuchen, Wettbewerber auszuschalten, deren Marktanteile zu übernehmen und zu einem marktführenden bzw. marktbeherrschenden Unternehmen zu werden. Hinsichtlich des betreffenden Marktes kann es sich um einen lokalen, nationalen oder den Weltmarkt handeln. In der Bundesrepublik Deutschland ist das Bundeskartellamt mit der Überwachung des Wettbewerbs betraut. Frage 10 a) Was versteht man unter den Opportunitätskosten (Alternativkosten) einer wirtschaftlichen Entscheidung, welche Informationen benötigt man, um sie zu bestimmen. (Beispiel) Opportunitätskosten geben an, welchen Wert man aufgeben würde, wenn man sich für eine Alternative entscheidet. Ein Beispiel dafür wären die Kosten einer entgangenen Miete, wenn man sie bezahlt um in einer eigenen Wohnung anstatt bei den Eltern zu wohnen. Informationen die man benötigt sind die Budgetrestriktion (wie viel Geld hab ich zur Verfügung), alle möglichen Alternativen, die sich anbieten, und die dazugehörigen Marktpreise. b) Sie gehen einer Teilzeitarbeit nach, aber ein Freund schlägt als Alternative einen Besuch im HSV-Stadion vor. Untersuchen Sie zunächst die Opportunitätskosten des Stadionbesuchs und danach die Opportunitätskosten der Teilzeitarbeit. Opportunitätskosten des Stadionbesuches: - Eintrittskarte entgangene Einnahme aus der Teilzeitarbeit Opportunitätskosten der Teilzeitarbeit: - c) Welches sind die Opportunitätskosten eines Kurzurlaubes (last-minute Flug nach Bologna für 1 Euro) während der Zeit der Semestervorlesungen? d) Erläutern Sie die konkreten Opportunitätskosten der Entscheidungen in Frage 7a, 7c, 8a und 8b. ???????????????????????? Frage 11 a) Ein HH verfügt über eine Konsumsumme von e = 2000 Euro. Er fragt zwei Güter (zb. Lehrbücher und Flugreisen) nach, deren Preise p1 = 40 Euro und p2 = 400 Euro sind. Die Nachfragemenge für Gut 1 sei mit x1 bezeichnet, die Nachfragemenge für Gut 2 mit x2. Ermitteln Sie die Budgetgleichung und zeichnen Sie die Budgetgerade in ein Koordinatensystem mit x1 auf der Ordinate und x2 auf der Abzisse. (Unterstellen Sie dazu, daß e vollständig ausgegeben wird und lösen Sie die Budgetrestriktion nach x1 auf.) . Markieren Sie den Bereich der realisierbaren Verbrauchspläne des HH. Die Budgetgerade ergibt sich zu : e = p1x1 +p2 x 2 . Löst man diese nach x1 auf, folgt: x1 = x1 50 e p2 - x2 . p1 p1 Der Bereich der realisierbaren Verbrauchspläne des HH, liegt unter der Voraussetzung, dass das ganze Einkommen e ausgegeben wird, auf der roten Gerade. Budgetgerade: x1 = e p2 - x2 p1 p1 5 x2 b) Berechnen Sie die Achsenabschnitte der Budgetgerade und erläutern Sie ihre jeweilige ökonomische Bedeutung. e e p2 e bedeutet, dass wenn der HH nur das - x 2 folgt mit x 2 = 0, x1 = . x1 = p2 p1 p1 p1 Gut 1 nachfragt, die Anzahl dieses Gutes von seinem Einkommen e und reziprok von dem Preis des Gutes 1 abhängt. Aus x1 = e e p2 e bedeutet, dass wenn der HH nur das - x 2 folgt mit x1 = 0, x 2 = . x 2 = p2 p1 p1 p2 Gut 2 nachfragt, die Anzahl dieses Gutes von seinem Einkommen e und reziprok von dem Preis des Gutes 2 abhängt. Aus x1 = Je billiger also das Gut, desto mehr kann der HH davon erwerben, bei konstantem Einkommen e. c) Berechnen Sie die Steigung der Budgetgerade und erläutern Sie ihre ökonomische Bedeutung. p dx e p2 - x 2 folgt die Steigung = 1 = - 2 . D.h. die Änderung der p1 p1 dx 2 p1 Güternachfrage entspricht dem umgekehrten negativen Verhältnis der Preise der beiden Güter. Aus x1 = Die Steigung der Budgetgeraden beträgt: (-)50/5 = -10 Dies bedeutet, dass man für eine weitere Flugreise auf 10 Lehrbücher verzichten muß! Dies sind dann die Alternativkosten einer zusätzlichen Flugreise in der Einheit Lehrbücher gemessen, die man für eine Reise aufgeben muß. d) Erklären Sie was man unter den Opportunitätskosten (Alternativkosten) des Konsums einer zusätzlichen Einheit von Gut 2 versteht. Wie lassen sich diese Opportunitätskosten zeichnerisch ermitteln? Wie groß sind hier diese Opportunitätskosten einer zusätzlichen Flugreise? ( |dx1/dx2| = p2/p1 = 10 Lehrbücher) Will man eine zusätzliche Einheit Gut 2 erwerben, braucht man 400€ dafür, deshalb muss man diese Summe vom Gut 1 abziehen, welche 10 Lehrbüchern entspricht, da eines 40€ kostet. Somit sind die Alternativkosten einer zusätzlichen Flugreise, 10 Lehrbücher. Rechnerisch ergibt sich diese aus: dx1 p2 400 = = =10 . dx 2 p1 40 d) Wie verändern sich die Opportunitätskosten für Gut 2, wenn sich der Preis für Gut 1 vervierfacht, während sich gleichzeitig der Preis für Gut 2 halbiert? (neue Zeichnung) ( von 400/40= 10 auf 200/160 = 1,25 !!!!!!!!!!! ) Von dx1 p2 0,5 400 dx1 p2 400 = = =1,25 . = = =10 auf dx 2 p1 4 40 dx 2 p1 40 e) Wie groß sind in d) die Opportunitätskosten des Konsums einer zusätzlichen Einheit von Gut1 , also eines zusätzlichen Lehrbuches? ( |dx2/dx1| = 160/200 = 0,8 ) Es ergeben sich die Opportunitätskosten zu dx 2 p1 4×40 = = = 0,8 . dx1 p2 0,5×400 f) Wie verändern sich die Opportunitätskosten, wenn sich gegenüber der Ausgangslage die Preise für beide Güter um 50 % erhöhen und sich gleichzeitig die Konsumsumme e um 100 % vergrößert? (neue Zeichnung). x1 66,67 4000 66,67 60 4000 6,67 600 50 5 6,67 x2 Frage 12 Bisher wurde vereinfachend unterstellt, die Wirschaftssubjekte entscheiden frei gemäß ihren individuellen Vorlieben über gegebene Alternativen, wobei alle relevanten Informationen vollständig zur Verfügung stehen. Welche Probleme müssten bei einer Entscheidung gelöst werden, wenn die Informationen über die Alternativen unsicher sind? (Ermittlung der objektiven oder der subjektiven Wahrscheinlichkeiten, Anwendung von bestimmten Verfahren wie des Maximin-Kriteriums, der Maximierung des Erwartungswertes oder der Auswahl der optimalen Alternative aus den verfügbaren Kombinationen von Erwartungswert und Risiko) Ist das die Antwort?? Was versteht man in dieser Situation unter einem Verhalten a) nach Bayes, Beim Verhalten nach Bayes sind die Wahrscheinlichkeiten für ein Eintreten der Einzelnen Fälle bekannt. Man entscheidet nun einfach nach dem höchsten Erwartungswert, der sich aus ( x) wi xi ergibt. i b) nach dem Prinzip des unzureichenden Grundes, Hierbei werden die Wahrscheinlichkeiten nicht als bekannt vorausgesetzt, sondern als gleich unterstellt. Jedes Eintreten der zur Verfügung stehenden Fälle hat folglich die 1 Wahrscheinlichkeit mit x als Anzahl der Fälle. Hiernach wird wieder nach dem höchsten x auftretenden Erwartungswert entschieden. c) nach dem Maximin-Kriterium Beim Maximum-Kriterium wird danach entschieden, in welchem Fall, bei welchem Gut das kleinste Minimum des Nutzens auftritt. Beispiel: Gut A B C Fall1 5 2 10 Fall2 -2 -1 -5 d) nach dem Optimismus-Pessimismus-Kriterium? Bei diesem Kriterium nimmt man eine Gewichtung des Zeilen-Maximums bzw. – Minimums vor. Der zu erwartende Nutzen wird mit diesen Anteilen in beiden Fällen bewertet und dann addiert. Beispiel: Gut A B C Fall1 5 2 10 Fall2 -2 -1 -5 Max 3/10 3/10 3/10 Min 7/10 7/10 7/10 E 0,1 -0,1 -0,5 (Dazu vgl. Schumann, I B h) Welche Probleme müssten bei einer Entscheidung gelöst werden, wenn das Ergebnis nicht nur von der eigenen Entscheidung, sondern auch von den Entscheidungen und Reaktionen der anderen Wirtschaftssubjekte abhängt. (Die voraussichtlichen Handlungen der anderen Individuen lassen sich nicht durch Wahrscheinlichkeiten erfassen, sondern nur dadurch bestimmen, daß man die verfügbaren Strategien, die möglichen Auszahlungen und die jeweiligen Zielsetzungen betrachtet.) Frage 13 a) Zeichnen Sie eine Produktionsmöglichkeitenkurve einer Volkswirtschaft für zwei Güter in ein Diagramm und nennen Sie die dahinter stehenden Annahmen. Gut A I oder II möglich, aber nicht III. I III II Gut B Bei diesem Modell wird eine Volkswirtschaft mit nur zwei Gütern vorausgesetzt. In der Produktionsmöglichkeitenkurve für zwei Güter sind die Möglichkeiten abzulesen, ein Gut in Abhängigkeit eines anderen mit gegebenen Produktionsgütern und gegebener Technik zu produzieren. Am Schnittpunkt der Kurve mit der Ordinate bzw. der Abszisse ist die Menge des Gutes abzulesen, wenn alle Produktionsfaktoren in nur ein Gut fließen. Die Funktion beschreibt eine Kurve, weil wenn man mehr des einen Gutes will, muß man die Produktion des anderen zurückschrauben, da sonst die Faktoren nicht ausreichen würden. Alles was aber an Kombinationen unter der Kurve liegt, ist möglich, alles was außerhalb liegt nicht. b) Erläutern Sie mit einer solchen Kurve den Zielkonflikt der Volkswirtschaft bei der Entscheidung zwischen der Produktion von PCs und der Produktion von PKW´s. Produktion PC / PKW Rubinfeld PC Tauschgerade Prod.-Punkt Wunschpunkt PKW c) Warum hat die Kurve eine negative Steigung? Wie oben erwähnt, hat ein Anstieg der Produktionsmenge des Produktes A eine Regression in der Menge des Produktes B aufgrund der beschränkten Produktionsfaktoren zur Folge. Daraus resultiert die negative Steigung der Kurve. d) Was bedeutet ein Punkt unterhalb der Kurve, was ein Punkt oberhalb der Kurve und was ein Punkt auf der Kurve? Punkte unterhalb der Kurve beschreiben einen Zustand, indem eine Güterkombination gefunden wurde, die die Produktionsfaktoren nicht vollständig ausnutzt. Es kann aufgrund des Mangels an diesen Faktoren keine Kombinationspunkt überhalb der Funktionskurve gefunden werden. Genau auf der Kurve werden alle Faktoren dann vollständig ausgenutzt. Eine Produktionssteigerung muß eine Einsparung beim anderen Produkt zur Folge haben. e) Wie kann man die Opportunitätskosten der PC-Produktion aus der Kurve ermitteln? Indem man die Steigung der Kurve in einem bestimmten Punkt ermittelt. Aus dieser Steigung ergeben sich dann die Opportunitätskosten einer zusätzlichen Einheit des Gutes B in Einheit Gut A gemessen, die man dann aufgeben müsste. f) Wie verändern sich die Opportunitätskosten der PC-Produktion für Produktionspunkte auf einer konvex nach außen gekrümmten Produktionsmöglichkeitenkurve? Geben Sie eine ökonomische Erläuterung für die ermittelte Veränderung. Gut A Gut B Da die Steigung der Kurve mit zunehmender Produktion des Gutes B stark zunimmt, nehmen auch die Opportunitätskosten stark zu! Dies bedeutet ökonomisch gesehen, dass jedes neu produzierte Gut B immer mehr Einheiten des Gutes A kosten. Hat am Anfang der Kurve ein weiteres Stück B noch kaum einen Einfluss auf die zu produzierende Menge des Gutes A, so lässt gegen Ende ein weiteres Stück B der Herstellung von A kaum noch Mittel über. g) Warum sind für einen Punkt unter der Kurve die Opportunitätskosten gleich Null? Weil in diesem Fall ein weiteres Stück vom Gut B nicht mit einer Verminderung der Produktion des Gutes A einhergeht. Dies ist erst wieder mit Erreichen der Kurve nötig. Gut A Gut B h) Wie verschiebt sich die Kurve, wenn die Ingenieure durch Technischen Fortschritt die PCProduktion effizienter gestalten? Die Kurve verschiebt sich wie in folgendem Schaubild. Es ist durch technischen Fortschritt möglich geworden, mit gleicher Menge an Produktionsfaktoren eine größere Menge an PCs herzustellen. [Der Fortschritt bei einem Gut kann gleichzeitig auch einen beim anderen Gut bewirken. Die eine Produktion hat oftmals in Bezug auf Know How oder gleich einsetzbare Neuerungen für beide Produkte u.ä. Auswirkungen auf andere Bereiche. ] PC PKW i) Wie ändern sich dadurch die Opportunitätskosten der PC-Produktion für ein beliebiges vorgegebenes Verhältnis von PC-Mengen zu PKW-Mengen (Etwa 1:1 oder 1:2)? Bei einer Steigerung der PC Produktion steigen auch die Opportunitätskosten der PCs. Denn wie im Schaubild ersichtlich wird die Steigung der Kurve in jedem ihrer Punkte größer. j) Wie verschiebt sich die Produktionsmöglichkeiten-Kurve, wenn in die Volkswirtschaft aus dem Ausland zusätzliche Arbeitskräfte und Kapitalgüter einströmen? (Zeichnung) Zusätzliche Arbeitskräfte und Kapitalgüter bedeuten zusätzliche Produktionsfaktoren. Somit können jeweils mehr Güter (wiederum in Abhängigkeit zueinander) produziert werden. Gut A Gut B Frage 14 Ein Unternehmer erwägt, 20 Euro in ein Projekt I oder ein Projekt II zu investieren, bei dem es jeweils drei mögliche Ergebnisse mit den folgenden Wahrscheinlichkeiten gibt: i Wahrscheinlichkeit wi 1 2 3 0,2 0,4 0,4 Projekt I Ertrag Xi Projekt II Ertrag Xi 100 Euro 50 Euro -25 Euro -40 Euro 10 Euro 85 Euro a) Berechnen Sie für das Projekt I und für das Projekt II jeweils den Erwartungswert der Erträge und die Standardabweichung s der Erträge (Maß für das Risiko). ( x) wi xi i s 2 w1 x1 E ( x) w2 x2 E ( x) 2 2 s s2 E I (X) = 0,2*100 + 0,4*50 + 0,4*(-25) = 30 s I (X) = 48,48 = [ 0,2(100-30)2 + 0,4(50-30)2 + 0,4(-25-30)2 ]0,5 E II (X) = 0,2*(-40) + 0,4*10 + 0,4*85 = 30 s II (X) = 48,48 = [ 0,2(-40-30)2 + 0,4(10-30)2 + 0,4(85-30)2 ]0,5 (Erwartungswert E(X) = w1X1 + w2x2 + w3X3 Standardabweichung s(X) = ( w1(x1-E(x))2 + w2(x2-E(x))2 + w3(x3-E(x))2 )0,5 Projekt I: 30 / 48,48 Projekt II: 30 / 48,48 Projekte haben hier gleiche Parameter ) b) Ein Unternehmer will auf jeden Fall investieren und entscheidet sich nach dem Maximin-Kriterium, was wird er tun? Wahl von Projekt I, da -25 größer ist als -40; wenn er auch die zusätzliche Alternative III "nicht investieren" prüft, würde er nicht investieren und Euro 20 sicher haben.) c) Erläutern Sie, was man unter einem risikoaversen Investor A, einem risikofreudigen Investor B und unter einem risikoneutralen Investor C versteht. Wie würden sie sich gegenüber Projekt I verhalten? (mit Begründungen) (A: investiert nicht B: investiert C: investiert) (Zum Verständnis vgl. Pindyck/Rubinfeld) Ein risikoaverser Investor A möchte am liebsten überhaupt kein Risiko bei einer Entscheidung eingehen. Er wird in Fall I nicht investieren. Ein risikofreudiger Investor B geht mit Blick auf einen hohen Gewinn auch ein hohes, bzw. höheres Risiko ein. Bei einem Erwartungswert, der wie hier über seinen Einsätzen liegt, wird er investieren. Auch der risikoneutrale Investor wird in Fall I sein Geld einsetzen, denn er schreckt zwar nicht vor Risiko zurück, will aber, dass der Erwartungswert der Investition über seinem Einsatz liegt. d) Der Investor A erwägt, zweimal 20 Euro zu investieren, nachdem man ihm erzählt hat, daß er durch "Diversifikation" , also durch Aufteilung der Resourcen auf verschiedene Projekte das Risiko seiner Gesamtanlage unter Umständen vermindern kann. Errechnen Sie den Erwartungswert und die Standardabweichung einer kombinierten Investition aus Projekt I und Projekt II. Was wird Investor A tun? (Projekt I + Projekt II: Der Erwartungswert beträgt 60 Euro, die Standardabweichung ist gleich 0 . Der risikoaverse Investor A wird investieren, weil er aus sicheren 40 Euro in der Ausgangslage hier 60 Euro erzielen kann, ohne das Risiko zu erhöhen) E I+II (X) = 30+30 = 60 ?????????????????? Warum ist s = 0? Frage 15 Betrachten Sie eine Lotterie mit drei möglichen Ergebnissen: 1. 100 Euro werden mit einer Wahrscheinlichkeit von 0,1 erzielt. 2. 50 Euro werden mit einer Wahrscheinlichkeit von 0,2 erzielt. 3. 10 Euro werden mit einer Wahrscheinlichkeit von 0,7 erzielt. a) Wie hoch ist der Erwartungswert der Lotterie? 27 b) Wie hoch ist die Varianz der Ergebnisse? 841 c) Wieviel würde eine risikoneutrale Person zahlen, um in der Lotterie mitzuspielen? Genau 27 Euro, denn da liegt der Erwartungswert der Lotterie. d) Wieviel würde eine risikofreudige Person für die Lotterie zahlen? Mehr als 27 Euro, weil sie neben dem Erwartungswert auch das Risiko, hier vebunden mit der Möglichkeit höherer Gewinne, positiv bewertet e) Wieviel würde eine sehr risikoabgeneigte Person für die Lotterie zahlen? Weniger als 27 Euro, bei sehr großer Risikoabneigung möglicherweise gar nichts. In beiden Aufgaben 14c und 15e wird untersucht, ob eine Situation I mit einem mit Sicherheit verfügbarer Betrag einer anderen Situation II mit einem bestimmten Erwartungswert und positivem Risiko vorgezogen wird, oder ob beide Situationen als äquivalent angesehen werden, oder ob Situation II der Situation I vorgezogen wird. Ein risikoaverser Mensch verlangt für die Übernahme des Risikos in Situation II eine sog. Risikoprämie, nur dann empfindet er beide Situationen I und II als gleichwertig. In 14c geht es darum, ob Situation I ( Ausgangssituation 20 Euro sicher, Risiko gleich Null) besser ist als Situation II (Investition mit Erwartungswert 30 Euro und Risiko s= 48). Nur in diesem Falle wird investiert. Ein risikofeindlicher Investor wird prüfen, ob die Risikoprämie in Höhe des zusätzlichen Erwartungswertes von +10 Euro ausreicht, um I zu verlassen und die Übernahme des Risikos in II zu rechtfertigen. Ein sehr risikofeindlicher Investor wird das verneinen und I vorziehen.. In 15e geht es darum, welche Situation I (welcher mit Sicherheit zu zahlende Preis der Lotterie) als angemessen empfunden wird, wenn man dafür eine Situation II (Lotterie mit Gewinn-Erwartungswert 27 und Gewinn-Varianz 841) erhält. Ein risikoaverser Lotteriespieler würde nur dann spielen (die Situation II der Situation I vorziehen), wenn er für die Übernahme des Risikos eine hinreichend große Prämie bekommt. Seine Prämie ergibt sich bei gegebenem Erwartungswert der Lotterie von 27 daraus, daß der Lotterie-Preis deutlich niedriger liegt als der Gewinn-Erwartungswert der Lotterie. Nur wenn die Prämie (Erwartungswert minus Preis) als angemessen empfunden wird, wird der risikoaverse Mensch Situation II wählen. Je höher seine Risikoabneigung und seine geforderte Risikoprämie, desto niedriger der von ihm akzeptierte Preis. In den Ihnen bekannten Lotterien liegen die Preise in der Regel wesentlich höher als die Gewinn-Erwartungswerte. Daraus kann man schließen, daß die Lotterie-Teilnehmer dort recht risikofreundig sind. Frage 16 In der Vorlesung haben wir den Fall einer Entscheidung zwischen zwei Anstellungsalternativen besprochen, die jeweils mit einer gewissen Wahrscheinlichkeit zu einem Ergebnis 1 und einem Ergebnis 2 führen können. Anstellung 1 Erwartetes Einkommen: 1500 Euro Standardabweichung 500 Anstellung 2 Erwartetes Einkommen: 1500 Euro Standardabweichung 99,50 (Zum Fall vergl. Pindyck/Rubinfeld Kapitel 5.1.3 Tabellen 5.1 und 5.3) Tragen Sie die beiden Alternativen als Punkte in ein Koordinatensystem mit dem erwarteten Einkommen auf der Ordinate und der Standardabweichung auf der Abzisse. Einkommen 1500 Standartabweichung s 99,5 500 Erläutern Sie, was man hier unter einem risikoaversen Investor A, einem risikofreudigen Investor B und unter einem risikoneutralen Investor C versteht. Wie würden sich A, B und C jeweils bei der Entscheidung zwischen den beiden Anstellungen verhalten? Frage 17 Ein Eigenheimbesitzer hat in seinem Haus Vermögensgegenstände im Wert von 50.000 Euro. In seiner Wohngegend muß er mit einer Wahrscheinlichkeit von 0,1 damit rechnen, daß im Laufe des Jahres in sein Haus eingebrochen wird und er einen Verlust von 10.000 Euro erleidet. Die Einbruchsversicherung kostet 1000 Euro pro Jahr. a) Errechnen Sie das erwartete Vermögen des Eigenheimbesitzers und die Standardabweichung s des Vermögens, - einmal für den Fall 1, dass er eine Versicherung abgeschlossen hat ( E(Vermögen) = 49.000 Euro ; s = 0) (Berücksichtigen Sie, dass das Vermögen hier in jedem Falle um die Kosten der Versicherung vermindert wird) Da er eine Versicherung abgeschlossen hat, bekommt er den gesamten Wert seines Vermögens erstatten. Es mindert sich nur um die Versicherungspolice: 50.000€ – 1000€ = 49.000€ - und einmal für den Fall 2, dass er keine Versicherung abgeschlossen hat. ( E(Vermögen)= 49.000 ; s = 3000) s² = 0,1 [] Konrad? Du machst doch gerade Statistik! Ich hab keinen Plan, was das alles mit VWL zu tun hat! b) Würde sich ein Hausbesitzer bei den gegebenen Versicherungskosten versichern oder nicht versichern, wenn er A- risikoneutral ist, B-wenn er riskoavers ist, C -wenn er risikofreudig ist? c) Würden sich A,B oder C versichern, wenn die Versicherung 2000 Euro pro Jahr kostet? ( Zur Erläuterung vgl. Pindyck/Rubinfeld Abschnitt 5.3.2) Frage 18 a) Was versteht man in einer spieltheoretischen Situation ganz allgemein unter einer dominanten Strategie? (Vgl. dazu Pindyck/Rubinfeld, Kapitel 13.1 und 13.2) Eine dominante Strategie ist für einen selber immer optimal, das heißt mit positivem Ausgang, egal welche Strategie der Gegner verfolgt. Analysieren Sie die folgenden strategischen Situationen (S1, S2, S3, S4 und S5) auf einem Markt mit jeweils zwei konkurrierenden Unternehmen auf der Angebotsseite. Jede Situation sei jeweils dadurch gekennzeichnet, daß beide Unternehmen ("Spieler") gleichzeitig entscheiden müssen und es keine Verhandlungen und Verabredungen zwischen Ihnen geben darf. b) Untersuchen Sie zunächst, ob die beteiligten Unternehmen jeweils (zb A und B in Frage 18) über eine dominante Strategie verfügen, die sie in jedem Falle vorziehen, egal was das jeweils andere Unternehmen macht. (Dazu müssen Sie einerseits ermitteln, welche Strategie für A optimal ist, wenn B die Strategie W wählt und andererseits, welche Strategie für A optimal ist, wenn B die Strategie kW wählt. Wenn die optimale Strategie für A in beiden Fällen die gleiche ist, handelt es sich um eine dominante Strategie für A, die in jedem Falle vorzuziehen ist. Danach prüfen Sie, ob es umgekehrt eine dominante Strategie für B gibt. Vgl. dazu Pindyck/Rubinfeld, Kapitel 13.1 und 13.2) c) Zeigen Sie, wie die Maximin-Strategie der beteiligten Unternehmen jeweils aussehen würde. Situation S1 Zwei Unternehmen A und B haben die Wahl, für Ihre Produkte zu werben oder nicht zu werben. Es ergeben sich die folgenden Auszahlungen für A und für B in Abhängigkeit der von beiden gewählten Strategien: Werbung Unternehmen B Werbung keine Werbung 10, 5 15, 0 Unternehmen A keine Werbung 6,8 10, 2 b) Für beide Unternehmen ist jeweils die Strategie W ("Werben") dominant. c) A hat Maximin-Strategie Werbung mit 10>6. B hat Maximin-Strategie Werbung mit 5 > 0. Situation S2 Werbung Unternehmen B Werbung keine Werbung 10, 5 15, 0 Unternehmen A keine Werbung 6,8 20, 2 b) Unternehmen A hat keine dominante Strategie mehr, seine optimale Strategie hängt ganz davon ab, was B tut. Unternehmen B dagegen hat die optimale Strategie "Werben" und wird diese Strategie wählen. Überlegen Sie, für welche Strategie sich A in dieser Situation entscheiden sollte.. c) A hat Maximin-Strategie Werbung mit 10 > 6. B hat Maximin-Strategie Werbung mit 5 > 0 . Situation S3 Die Nahrungsmitteldiscounter "A" und "L" konkurrieren in diesen Tagen mit einem ähnlichen Produkt (500 gr Kaffee) um die Nachfrage auf einem speziellen Markt, wobei die erzielbaren Gewinne von der Preispolitik abhängen, und zwar sowohl vom eigenen Preis als auch vom Preis des Konkurrenten. Beide Unternehmer müssen ihren Preis zur gleichen Zeit festlegen und dürfen keine Preisabsprachen treffen. Zur Wahl steht eine Hochpreisstrategie S2 (2,20 Euro) und eine Niedrigpreisstrategie S1 (1,99 Euro) mit folgender GewinnAuszahlungsmatrix (in 10.000 Euro): S1: 1,99 Euro Unternehmen "L" S1: 1,99 Euro S2: 2,20 Euro 12,12 29,11 Unternehmen "A" S2: 2,20 Euro 3,21 20,20 b) (Für beide ist die Niedrigpreisstrategie S1/S1 dominant. c) (A: Strategie S1 ist Maximin-Strategie mit 12 > 3. B: hier ist ebenfalls Strategie S1 Maximin-Strategie mit 12 > 11) Die Spieler werden bei gleichzeitigem unabgesprochenen Handeln beide die agressive PreisStrategie S1 mit dem Niedrigpreis wählen, weil diese Strategie, unabhängig von der Strategie des Gegners optimal ist. Gerade hat auch "A" den Kaffeepreis auf 1,99 gesenkt. Die Gewinne für beide sind 12,12 . Erläutern Sie, warum es hier nicht gelingt, das für beide viel bessere Ergebnis 20,20 zu erreichen. (Es exisiert hier ein sog. Gefangenen-Dilemma, das in der nächsten Vorlesung erklärt wird: Das insgesamt optimale Ergebnis 20,20 wird nicht erreicht, weil bei einer Strategiewahl S2 jeder Unternehmer befürchten muss, vom Mitbewerber durch Strategie S1 unterboten zu werden, weil das besser für ihn wäre. Eine Strategie S2 ist daher ohne feste Vereinbarung für jeden zu riskant.) Situation S4 Zwei Fluggesellschaften I und II entscheiden über Ihre Flugregion, sie können entweder in Nordeuropa fliegen oder in Südeuropa. Fluggesellschaft II S1: Nordeuropa S1: Nordeuropa Fluggesellschaft I 100, 600 S2: Südeuropa 500,900 S2: Südeuropa 200,800 400,500 b) Es gibt keine dominante Strategie für A, und auch keine dominante Strategie für B. In der nächsten Vorlesung lernen Sie das allgemeine Konzept des Nash-Gleichgewichtes kennen, das in dieser Situation weiter helfen kann. c) Maximin-Strategie für I ist S2. Maximin-Strategie für II ist S1. Situation S5 Analysieren Sie die Auszahlungsmatrix des folgenden nichtkooperativen Spiels zweier Spieler mit jeweils drei Strategien: B S21 S22 S32 S11 8,-8 1,1 -8,8 A S12 1,1 2,2 1,1 S13 -8,8 1,1 8,-8 c) Es gibt auch hier keine dominante Strategien für A oder für B. Auch hier gibt es Maximin-Strategie für A ist S12 . Maximin-Strategie für B ist S22 Frage 19 a) Erläutern Sie ausführlich, was man unter einem Nash-Gleichgewicht versteht. (Vgl. Pindyck/Rubinfeld 13.3. Es handelt sich dabei um eine Strategie-Kombination, bei der jeder Spieler unter Berücksichtigung der gegebenen Handlung des Gegners für sich das Bestmögliche tut. Beide tun das Bestmögliche bei gegebenen Entscheidungen des anderen. Kein Spieler hat damit einen Anreiz, von dieser zunächst gewählten Strategie abzuweichen.) b) Untersuchen Sie die Situationen S2, S4 und S5 aus Frage 18 darauf hin, ob es ein oder mehrere Nash-Gleichgewicht/e gibt. (S2: W/W (10,5) S4: S2/S1 (200,800) und S1/S2 (500,900) S5: S12/S2 (2, 2) Es handelt sich um Strategiekombinationen, bei denen wechselseitig jeweils die Strategie des einen Spielers die beste Antwort auf die jeweils gewählte Strategie des anderen Spielers darstellt, sodaß kein Spieler eines nicht-kooperativen Spiel im Nachhinein einen Anlaß hat, seine Strategie zu wechseln. Achtung: Sie müssen nacheinander jede mögliche StrategieKombination prüfen!) Reicht dass als Antwort? c) Erläutern Sie am Beispiel der Situation S3, daß ein Gleichgewicht in zwei dominanten Strategien in jedem Fall ein Nash-Gleichgewicht sein muß (Sonderfall eines NashGleichgewichtes) S1: 1,99 Euro Unternehmen "L" S1: 1,99 Euro S2: 2,20 Euro 12,12 29,11 Unternehmen "A" S2: 2,20 Euro 3,21 20,20 Beispiel S3 zeigt, dass sowohl für A als auch für B die Strategie S1 die dominante ist. Es handelt sich hierbei um ein sog. „Prisoners Dilemma“! Beide Discounter würden mit S2 besser dastehen, sprechen sich aber nicht ab und wählen deshalb nicht die optimale Lösung. Prisoners Dilemma Gefangener B gestehen: 1,99 Euro gestehen: 1,99 Euro -5,-5 nicht gest: 2,20 Euro -1,-10 Gefangener A nicht gest: 2,20 Euro -10,-1 -2,-2 Jahre Haft Da sich gefangene nicht absprechen können vor ihrer Aussage, ist es ein zu großes Risiko für beide nicht zu gestehen. Gesteht dann nämlich der andere, erhöht sich die Strafe für den nicht gesteher! Folge beide gestehen (dom. Strategie) Frage 20 Die Käufer und die Verkäufer auf einem Markt habe die folgenden Nachfragepläne bzw Angebotspläne: Preis in Euro 4 5 6 7 8 9 Nachfragemengen(Stück) 135 104 81 68 53 39 Angebotsmengen (Stück) 26 53 81 98 110 121 a) Zeichnen Sie die Angebotskurve und die Nachfragekurve für diesen Markt in ein PreisMengen-Diagramm. P A1 y(p) 6 D1 x(p) y,x 0 81 b) Wie hoch sind auf diesem Markt der Gleichgewichtspreis und die Gleichgewichtsmenge? Am Schnittpunkt der beiden Kurven sind Angebot und Nachfrage im Gleichgewicht! Hier lassen sich die Gleichgewichtsmenge (81) und der Gleichgewichtspreis (6) ablesen! c) Erläutern Sie, welche Marktteilnehmer im Gleichgewicht (b) ihre Pläne nicht realisieren können? Anbieter, die für ihre Ware mehr als 6 € verlangen, werden nichts verkaufen. Bitte prüfen! d) Was würde geschehen, wenn der tatsächliche Marktpreis mit 9 Euro deutlich über bzw mit 4 Euro deutlich unter dem Gleichgewichtspreis läge? Welche Marktteilnehmer könnten dann ihre Pläne nicht realisieren?(mit Zeichnung) P x(p) Überschußangebot y(p) P0 P* PU Überschußnachfrage 0 y,x y*/x* Aus einem zu hohen Pries resultiert ein Angebotsüberschuss. Die Folge daraus ist ein Druck durch den Markt, die Preise zu senken. Liegt der Preis unter dem Gleichgewichtspreis, so wird man eine Überschussnachfrage erleben, da sehr viele Leute die Ware zu so einem günstigen Preis kaufen möchten. Der Preis wird sich dann durch diese vielen Nachfrager wieder nach oben verschieben. Frage 21 Der Zusammenhang zwischen Eintrittspreisen und Sitzplätzen in einem kleinen Fußballstadion ist durch die folgende Angebots- und Nachfragetabelle dargestellt. Preis p in Euro Nachfragemenge (Stück) 4 8 12 16 20 Angebotsmenge (Stück) 10 000 8 000 6 000 4 000 2 000 8000 8000 8000 8000 8000 a) Zeichen Sie die Angebots- und die Nachfragekurve in ein Preis-Mengendiagramm und diskutieren Sie ihren Verlauf. P A 20 16 12 8 D 4 x 2000 4000 6000 8000 10000 Die Nachfragekurve hat wie erwartet einen Verlauf mit negativer Steigung. Je teurer ein Ticket im Stadion ist, desto weniger Karten werden gekauft. Nichts desto trotz aber bietet der Stadionbetreiber immer dieselbe Menge an Karten an. Der Gleichgewichtspreis liegt bei 8€. Geht man davon aus, dass er immer alle seine Plätze besetzt haben will, so darf der Preis nicht über 8€ liegen, weil sonst keine 8000 Karten mehr verkauft werden. b) Wie hoch sind der Gleichgewichtspreis und die Gleichgewichtsmenge? Gleichgewichtspreis = 8€ Gleichgewichtsmenge = 8000 Karten c) Durch die Schliessung einer benachbarten Anlage des Ortes kommt Nachfrage hinzu: Preis in Euro zusätzliche Nachfragemenge (Stück) 4 4000 8 3000 12 2000 16 1000 20 0 Ermitteln Sie die neue Angebots- und Nachfragekurve, zeichnen Sie die Kurven und geben Sie die neuen Gleichgewichtswerte an. ( p* = 12 x* = 8000) Preis p in Euro Nachfragemenge (Stück) Angebotsmenge (Stück) 4 8 12 16 20 14 000 11 000 8 000 5 000 2 000 8000 8000 8000 8000 8000 P A 20 16 12 D´ D 8 4 x 2000 4000 6000 8000 11000 14000 Der Gleichgewichtspreis steigt bei dieser steigenden Nachfrage auf 12 € bei einer ebenfalls verkauften Menge Karten von 8000 Stück! Frage 22 Zeichnen Sie die im folgenden aufgeführten Nachfragefunktionen zweier HH nach einem Gut (z.B Schweinefleisch) in jeweils ein Preis-Mengen-Diagramm und leiten Sie daraus die aggregierte Nachfragekurve für dieses Gut grafisch und algebraisch her (mit Erläuterungen) HH1: p = -3x1 + 21 ( p = Preis des Gutes; x1 , x2 nachgefragte Gütermengen der beiden HH) HH2: p = -x2 +7 (Bei der grafischen Aggregation müssen für jeden denkbaren Preis p die einzelnen Nachfragemengen horizontal addiert werden; Zur algebraischen Herleitung müssen Sie die Nachfragefunktionen zunächst nach den Mengen x(p) als Funktion des Marktpreises auflösen. Sodann werden die Mengen für jeden Preisbereich addiert, in dem die einzelne Nachfrage jeweils auftritt. Abschließend werden die Nachfragefunktionen wieder zum Preis p(x) hin aufgelöst. Die Gesamtnachfragekurve hat bei p= 7 einen "Knick": Für: p >7 ist p = -3x + 21 und für 0 <= p <= 7 ist p = -(3/4)x + 42/4 Vgl.Schumann: IB7d ). P 21 7 x1 HH1 x2 HH2 x 1+x 2 1 p1 7 3 x2 ( p ) p 2 7 x1 ( p) 4 p 14 3 3 42 umformen p( x) x 4 4 x1 ( p) x2 ( p) Frage 23 a) Unterscheiden Sie sorgfältig die Begriffe "Angebotskurve" und "angebotene Menge" bzw "Nachfragekurve" und "nachgefragte Menge". Die angebotene Menge bzw nachgefragte Menge entspricht nur einem bestimmten Punkt auf der Angebots- bzw Nachfragekurve. Es handelt sich genau um die Menge, die bei einem bestimmten Preis gemäß der Angebotskurve und gemäß der Nachfragekurve geplant wird. b) Erläutern Sie mögliche Ursachen, die im allgemeinen eine Nachfragekurve nach rechts oder nach links verschieben könnten. Erläutern Sie die Ursachen für die Verschiebung einer Angebotskurve nach rechts oder nach links . Die Nachfragekurve wird im allgemeinen nach rechts verschoben, wenn die Nachfrage nach einem Gut steigt, nach links läuft sie, wenn die Nachfrage fällt. Dies kann verschiedene Gründe haben, z.B. Leute möchten kein Bier mehr kaufen, weil die BILD aus versehen geschrieben hat, dass man davon betrunken wird ;-) Die Angebotskurve läuft nach rechts, wenn z.B. nach einer guten Kohlernte mehr Kohl für den gleichen Preis angeboten werden kann, als im Vorjahr. Nach links geht es, wenn es eine schlechte Ernte war. Die Konsequenz dieser Verschiebung ist es, dass der einzelne Kohlkopf dieses Jahr teurer ist. c) "Bei einer bestimmten Verschiebung der Angebotskurve beeinflussen sowohl die Steigung der Angebotskurve als auch die Steigung der Nachfragekurve die Veränderung der Gleichgewichtsmenge". Trifft diese Aussage zu? Geben Sie Erläuterungen unter Verwendung von Diagrammen. P N´ Das resultierende Gleichgewicht ist immer abhängig von beiden Kurven! A´ A N y,x Die Aussage trifft zu, denn die Menge kann fallen, auch wenn sich die Nachfrage nach rechts verschiebt. Frage 24 Marktforscher haben für einen bestimmten Gütermarkt die folgende Nachfragefunktion ermittelt: xN = 1600 -300p xN = Nachfragemenge p = Güterpreis in Euro xA = Angebotsmenge Die Angebotsfunktion sei: xA = 1400 + 700p a) Berechnen Sie den Gleichgewichtspreis und die Angebotsmenge und die Nachfragemenge bei diesem Preis. ( p* = 0,2 xA* = xN* = 1540 ) xN x A p* 0,2 x N * x A * 1540 b) Wie groß ist der Angebotsüberschuß, wenn sich der Preis gegenüber dem Gleichgewichtspreis verdoppelt? (200) p *2 0,4 x N 1480 x A 1680 P A P** P* D 0 y,x 1480 1680 Der Angebotsüberschuss beträgt also 200! Frage 25 a) Beschreiben Sie zunächst algebraisch das Konzept der Preiselastizität der Nachfrage und das Konzept der Einkommenselastizität der Nachfrage und erläutern Sie jeweils präzise, was diese Konzepte jeweils ganz genau messen. x x p ηx;p = x = (wird relativ angegeben) p p x p (p Marktpreis (Dimension: Euro/kg) , x nachgefragte Menge (Dimension: kg), e Einkommenshöhe (Dimension: Euro)). (Vgl. Schumann IB4e; Pindyck/Rubinfeld 2.4 und 4.3.1. und 4.3.2) Preiselastizität hab ich zwar schon mal in BWL oder so gemacht, aber vllt habt ihr ja was anderes gemacht, als ich nicht mehr da war! Alle mit E. lass ich also erstmal aus! b) In welcher Dimension wird die Preiselastizität der Nachfrage gemessen und in welcher Dimension die Einkommenselastizität der Nachfrage? c) Welche Vorteile hat die Verwendung von Preis-Elastizität zur Messung der Nachfragerreaktionen gegenüber der Verwendung etwa der Preis-Sensitivität (dx/dp) ? d) Erläutern Sie das Verhalten eines HH1 mit einer Preiselastizität der Nachfrage für Benzin von -1,5 und eines HH2 mit einer Preiselastizität von -1. e) Erläutern Sie das Verhalten eines HH1 mit einer Einkommenselastizität der Nachfrage für Automobile von +1. und eines HH2 mit einer Einkommenselastizität von +3. f) Was versteht man genau unter der Preiselastizität des Angebots? Erläutern Sie das Verhalten einer Unternehmung mit einer Preiselastizität des Angebotes von +2. (Achtung: Alle Elastizitäten beziehen relative Größen aufeinander, z.B. prozentuale Änderungen einer Wirkungsvariable auf prozentuale Änderungen einer Ursachenvariable. Die muß immer ganz klar zum Ausdruck gebracht werden) Frage 26 Drei Fahrer A, B und C mit häufig wechselnden Einkommenshöhen fahren regelmäßig zum tanken. Fahrer A will, unabhängig von den derzeit auftretenden Preisschwankungen und Einkommensschwankungen, stehts ein Zwanzigstel seines Einkommens für Benzin ausgeben. Fahrer B tankt immer genau 60 Liter; Fahrer C tankt immer für exakt für 80 Euro. Wie groß ist jeweils die Einkommenselastizität und die Preiselastizität der Benzinnachfrage der drei Fahrer? ( Denksportaufgabe!!! A E-El: +1, P-El: -1 / B E-El: 0, P-EL: 0 / C E-El: 0, PEL: -1 Sie müssen ausgehen von der formalen Definition für die Einkommenselastizität der Nachfrage und für die Preiselastizität der Nachfrage. Bei der numerischen Bestimmung dieser Elastizitäten tritt in dieser Aufgabe das Problem auf, dass sich sowohl die Einkommen als auch die Preise gleichzeitig ändern. (wie es in der Realität auch passieren kann). Es gibt hier dann 2 mögliche Ursachen für das beobachtbare Nachfrageverhalten. Man muss zunächst überlegen, was es für die mengenmäßige Benzinnachfrage bedeutet, wenn die Fahrer A,B,C sich bei wechselnden Einkommenshöhen und wechselnden Preishöhen so verhalten wie angegeben und welcher Zusammenhang sich daraus dann zwischen den relativen Änderungen der Benzinnachfrage und den relativen Änderungen des Einkommens einerseits und den relativen Änderungen der Preise andererseits ergibt.) Frage 27 a) Die Nachfragefunktion eines HH nach einem Gut sei durch p = 20 - 0,5x gegeben. (p Marktpreis; x nachgefragte Menge). Zeichnen Sie den Graph der Funktion und bestimmen Sie den `Prohibitivpreis´ (Preis, bei dem die Nachfragemenge Null ist) ( 20 ) und die `Sättigungsmenge´ (Menge, die bei einem Preis von Null nachgefragt wird) ( 40 ). P 20 Nachfragefunktion p = 20 - 0,5x 0 y,x 40 Prohibitivpreis: p = 20 – 0,5*0 p=20 Sättigungsmenge: 0 = 20 – 0,5x x = 40 b) Errechnen Sie für die gegebene Funktion die Preiselastizität der Nachfrage für x = 10. ( -3) x p (2) 1,5 3 p x c) Errechnen Sie für die gegebene Funktion die Preiselastizität der Nachfrage für p = 10. ( -1). x p (2) 0,5 1 p x d) Begründen und erläutern Sie ausführlich, wie sich die Nachfrageelastizität entlang der gegebenen linearen Nachfragekurve verändert. (Grafische Herleitung und Analyse). e) In welchem Preisbereich und in welchem Mengenbereich ist diese Nachfragefunktion unelastisch? (Zur Abgrenzung dieser Bereiche ist es zunächst erforderlich, den AbgrenzungsPunkt auf der Nachfragekurve mit der Elastizität -1 zu bestimmen; danach bestimmen Sie den Preisbereich bzw den Mengenbereich für Punkte auf der Nachfragekurve, deren Elastizitäten, absolut genommen, kleiner als eins sind |(dx/dp)(p/x)| < 1 ). Frage 28 Im Jahre 1998 haben die Amerikaner 23,5 Mrd Päckchen (Pk) Zigaretten geraucht (=470 Mrd Zigaretten) . Der durchschnittliche Einzelhandelspreis betrug 2 $ pro Päckchen . Auf dem Zigarettenmarkt war 1998 ein Marktgleichgewicht. Statistische Untersuchungen haben gezeigt, daß die Preiselastizität der Nachfrage -0,4 und die Preiselastizität des Angebots + 0,5 betrug. Verwenden Sie diese Informationen zur Herleitung einer linearen Nachfragefunktion und einer linearen Angebotsfunktion für den amerikanischen Zigarettenmarkt. (Vgl. Pindyck/Rubinfeld 2.6 . Wenn man unterstellt, daß die Angebotskurve und die Nachfragekurve jeweils eine Gerade ist, kann man die jeweilige Geradengleichung aus Informationen über einen Kurvenpunkt und den Wert der Elastizität in diesem Punkt bestimmen: Nachfragekurve x = a + bp ; Angebotskurve y = c + dp ; a,b,c,d sind die Konstanten der Funktionen. Aus der Definitions-Gleichung für die Nachfrage-Elastizität von -0,4 im Gleichgewichtspunkt ermittelt man b = dx/dp = -4,7x109 (Pk/$). Durch Einsetzen in die Nachfragekurve erhält man a = 32,9x109 (Pk) Es ergibt sich also x = 32,9x109 - 4,7x109 p. Analog erhält man für die Angebotskurve y = 11,75x109 + 5,875x109 p . Kontrolle der Gleichgewichtswerte: Für x = y ergibt sich p* = 2 und x* = 23.5x109 ) Frage 29 Zeichnen Sie folgende Nachfragekurven in ein (p-x)-Diagramm: eine vollkommen preisunelastische Nachfragekurve, eine völlig preiselastische Nachfragekurve, eine vollkommen preisunelastische Angebotskurve und eine völlig preiselastische Angebotskurve. Erläutern Sie jeweils die dahinter stehenden Verhaltensweisen und geben Sie ein praktisches Beispiel für jeden Extremfall. Frage 30 Gegeben sei folgende Nachfragekurve: p = 0,5x-1 (mit p= Güterpreis und x= Gütermenge) . a) Berechnen Sie die Preiselastizität der Nachfrage für die Punkte auf der Kurve bei p=1 , p=2 und für p=3 und erläutern Sie den Befund. ( Isoelastische Kurve mit Preiselastizität von -1; sog. Eins-elastische Kurve. Vgl. Pindyck/Rubinfeld 4.3.2 und Schumann. IB4e) b) Bei welchem Preis ist der Marktumsatz px am größten? (Der Marktumsatz ist mit 0,5 überall gleich groß) Frage 31 Erläutern Sie denkbare Ursachen für a) eine Verschiebung der Güternachfragekurve für PKW nach links. Eine Verschiebung der Nachfragekurve nach links bedeutet, dass weniger PKWs nachgefragt werden, somit steigen sie im Preis. Mögliche Ursachen hierfür können die steigenden Benzinpreise sein. b) eine Verschiebung der Güterangebotskurve für PKW nach rechts. Eine Verschiebung der Angebotskurve nach rechts bedeutet, dass man mehr Autos für den selben Preis bekommt. Das bedeutet, dass sie im Preis fallen. Es werden mehr Autos angeboten. Ein Grund hierfür kann sein, dass es der Autoindustrie schlecht geht, weil die Leute aufgrund der hohen Benzinpreise immer weniger Auto fahren. d) Was wird auf dem PKW-Markt passieren, wenn sich gegenüber der Ausgangssituation beide Kurven wie angegeben verschieben? P A N´ A´ N y,x Frage 32 Wie lassen sich die folgenden Marktvorgänge durch Verschiebung der Angebotskurve und/oder der Nachfragekurve möglichst einfach erklären (jeweil eine Grafik im (p,x)Koordinatensystem): a) Marktpreis p steigt und gleichzeitig steigt die gehandelte Menge x . P A Nachfrageschock N´ Schnittpkt.= (A;N´) N y,x b) p steigt, x sinkt. P A´ N Schnittpkt.= (A´;N) A y,x c) p sinkt, x sinkt. P A Nachfrageschock N´ Schnittpkt.= (A;N´) N y,x d) p sinkt, x steigt. P A N Angebotsschockschock A´ Schnittpkt.= (A´;N) y,x e) p steigt, x bleibt unverändert. P A´ Schnittpkt.= (A´;N´) N A N´ y,x f) p sinkt, x bleibt unverändert. P A Schnittpkt.= (A´;N´) N´ A´ N y,x g) p bleibt unverändert, x steigt. P A Schnittpkt.= (A´;N´) N A´ N´ y,x h) p bleibt unverändert, x fällt. P A´ Schnittpkt.= (A´;N´) N´ A N y,x Frage 33 a) Welche der folgenden Güterkombinationen sind Komplementärgüter und welche sind Substitutionsgüter: -Vorlesung in Statistik/Vorlesung in Volkswirtschaftslehre (Komplementär) -Gleiche Vorlesungen wie oben, aber die Vorlesungen überschneiden sich zeitlich. (Substitution) -Tennisbälle und ein Tennisschläger (Komplementär) -Eine Flugreise und eine Zugreise nach München am 24.12.2004 (Substitution) -PKW und Benzin (Komplementär) Frage 34 Nehmen Sie an, der HSV wandelt sich in eine AG um und geht an die Börse. Es sollen 3000 Aktien angeboten und in jedem Falle ausgegeben werden. Die mit der Neuemission betraute Bank ermittelt für die Aktie zur Zeit folgende Nachfragekurve der potentiellen Anleger: p = 7000 - 2x (p Aktienpreis, x geplante mengenmäßige Aktiennachfrage). Zeichnen Sie die Marktsituation und bestimmen Sie den markträumenden Anfangspreis, bei dem die geplante Angebotsmenge gleich der geplanten Nachfragemenge ist. (p* = 1000) x 3000 p * (3000) 7000 2 * 3000 1000 Welche Marktsituationen ergäben sich bei einem Emissionspreis von 3500 bzw bei einem Emissionspreis von 50 ? Bitte überprüfen! 3500 7000 2 x x* 1750 50 7000 2 x x* 3475 Frage 35 Das Ölangebot der OPEC sei völlig preisunelastisch. Nachdem die Ölpreise mit 18 $ je Barrel auf den tiefsten Stand der vergangenen dreieinhalb Jahre gefallen waren, wollte das Kartell der Förderländer (OPEC) vereinbaren, die Angebotsmengen um 5 % zu kürzen. Das Kartell strebte damit nach eigenen Aussagen einen Preis von 27 $ je Barrel an. - Erläutern Sie die Wirkung dieser Maßnahme in einem Angebots-Nachfrage-Diagramm bei gegebener Nachfragekurve. - Von welcher kurzfristigen Preiselastizität der Ölnachfrage ging die OPEC in ihrer Argumentation offensichtlich aus? ( - 0,1) - Welche langfristigen Reaktionen der Nachfrager nach Öl sind bei einer so deutlichen Preissteigerung denkbar, wie könnte sich die Preiselastizität langfristig ändern und wie könnte sich die Nachfragekurve langfristig verschieben? Welchen Einfluß hätte die langfristige Reaktion der Nachfrager auf den Ölpreis? (AngebotsNachfrage-Diagramm). Frage 36 Verwenden Sie Angebots- und Nachfragekurven zur Illustration, um zu zeigen, warum jedes der folgenden Ereignisse den Butterpreis und die Menge der gekauften und verkauften Butter auf dem Markt für Butter beeinflusst: a) Ein Anstieg des Margarinepreises; b) ein Anstieg des Milchpreises; c) eine Zunahme des durchschnittlichen Einkommensniveaus; d) Eine TV-Sendung über Ursachen des Herzinfarktes mit drastischen Bildern aus dem OP, die vor übermäßigem Butterkonsum warnt. Bekloppt oder was? Frage 37 Ein einzelner Anbieter (Monopolist) steht vielen Nachfragern mit der folgenden MarktNachfragekurve gegenüber: p = 3x-1 . Er verkauft sein Produkt gegenwärtig zu einem Preis von p = 0,5. Um seinen Erlös zu erhöhen, erwägt der Monopolist, den Verkaufspreis zu erhöhen a) Wie hoch ist der Erlös in der Ausgangslage? ( px = 3) p 3* 1 Erlös px 3 x b) Prüfen Sie, ob dieser Erlös durch Preiserhöhungen vergrößert werden kann und diskutieren Sie das Ergebnis unter Verwendung der Preiselastizität der Nachfrage. c) An anderer Monopolist steht der folgenden Nachfragekurve gegenüber: p = 2 - 0,25x . Auch er erwägt, den Kaufpreis zu erhöhen, um seinen Erlös zu vergrößern. Prüfen Sie auch hier, ob der Erlös durch Preiserhöhungen vergrößert werden und diskutieren Sie, von welchen Ausgangspunkten auf der Nachfragekurve aus dies möglich ist bzw von welchen anderen Ausgangspunkten dies nicht möglich ist. Frage 38 a) Warum unterscheiden sich langfristige Nachfrageelastizitäten von kurzfristigen Nachfrageelastizitäten? b) Betrachten Sie die zwei Güter "Benzin" und "Automobile". Erwarten Sie Sie, daß die Preiselastizitäten nach Benzin kurzfristig oder langfristig größer sind (Absolutbeträge!)? Begründen Sie Ihre Erwartung. Wie verhält es sich mit den kurzfristigen und langfristigen Preiselastizitäten nach Automobilen? c) Erläutern Sie unter Berücksichtigung der kurzfristigen und der langfristigen Einkommenselastizitäten der Nachfrage, warum die Maschinenbaubranche im Konjunkturablauf erheblich stärkeren Produktionsschwankungen unterliegt als die Nahrungsmittelindustrie. Was könnte daraus für die Einstellungschancen junger Wirtschaftsingenieure folgen? (Vergl. Pindyck/Rubinfeld 2.5 . Für viele kurzlebige Verbrauchsgüter ist zu beobachten, daß die Wirtschaftssubjekte einige Zeit benötigen, um ihre Konsumgewohnheiten zu ändern, nachdem sich die Güterpreise oder die Einkommen geändert haben. Bei vielen langlebigen Gütern (zb. Automobile, Maschinen, Küchenherde, TV-Geräte, PC) wird der Gesamtbestand optimiert und die kurzfristigen Nachfrageströme in einem Jahr ergeben sich aus der erforderlichen Erneuerung alter Geräte und zusätzlich aus den eventuell gewünschten Bestandsänderungen. In der Regel ist der vorhandene Gesamtbestand dieser Güter wesentlich größer als die jeweilige Jahresproduktion (für den Ersatzbedarf) . Dies kann dazu führen, daß selbst kleine gewünschte Bestandserhöhungen/Bestandssenkungen kurzfristig zu einer vergleichsweise großen Zunahme/Abnahme der laufenden Nachfrage führt. Ebenso wirken etwa durch Preiserhöhungen eines langlebigen Gutes bedingte (nur begrenzt mögliche) Verschiebungen des "normalen" Ersatzzeitpunktes in die Zunkunft kurzfristig stark negativ auf die Nachfrage. Langfristig normalisiert sich dieser Effekt wieder. Dies kann man leicht an Beispielen zeigen.) Frage 39 a) Welche Wirkung hat es auf den Marktpreis p und die gehandelte Menge x des Marktes für Grünköhl, wenn die Bauern in einem Jahr eine völlig neu entwickelte Sorte Grünkohl anbauen, die bei völlig gleichen Produktionskosten und völlig gleicher Qualität 100% mehr Ertrag als die alte Sorte bringt. (Analyse mit Marktdiagramm) P A A´ P* P** y Der Verbraucher freut sich über billigere Ware, aber der Landwirt kämpft mit sinkenden Erlösen! b) In welche Richtung wird sich der Umsatz px der Bauern durch die neue Sorte verändern, wenn Sie davon ausgehen, daß die Nachfrager nach Grünkohl insgesamt relativ preisunelastisch reagieren? (Erläuterungen der Steigung der Nachfragekurve und der Marktsituation mit einem Marktdiagramm) Nachfragekurve mit hoher Preiselastizität: P Schon eine kleine Preisänderung hat starke Auswirkungen auf die abgesetzte Menge. 0 x Nachfragekurve mit sehr niedriger Preiselastizität: P Der Preis muß sehr stark fallen, um neues Gleichgewicht zu erreichen 0 x c) Was vermuten Sie, wie werden die Bauern die Einführung der neuen Sorte beurteilen? Wie werden die Konsumenten die Einführung der neuen Sorte beurteilen? Die Erlöse des Bauern sinken, da der Preis für Grünkohl aufgrund der steigenden Menge auf dem Markt fällt! Frage 40 a) Erläutern Sie, was man unter dem "Markt für Schokoladen-Weihnachtsmänner" in Deutschland genau versteht. Unter dem „Markt für Schokoladen-Weihnachtsmänner“ versteht man die Angebots- und Nachfragemodalitäten zwischen den Herstellern für diese Weihnachtsmänner und deren Konsumenten. Der Markt steht sinnbildlich für das Aufeinandertreffen von Angebot und Nachfrage. b) Zwei Haushalte A und B haben folgende Nachfragepläne bezügl. der W-Männer: Die Produzenten von W-Männern C haben zusammen folgende Angebotspläne: p (Euro) 0,00 0,50 1,00 1,50 2,00 2,50 3,00 3,50 (A) x (Stück) 12 10 8 6 4 2 0 0 (B) x (Stück) 7 6 5 4 3 2 1 0 (C) y(Stück) 3 4 5 6 7 8 9 10 Zeichnen Sie die Nachfragekurve von (A) und die Nachfragekurve von (B) in jeweils ein Diagramm. Wie groß ist der Prohibitivpreis und die Sättigungsmenge von (A) und von (B)? Ermitteln und zeichnen Sie die aggregierte Nachfragekurve von (A) und (B) für W-Männer. 1 p A x 12 x A 4 p A 48 4 1 pB x 7 xB 2 pB 14 2 xges x A xB 4 p 2 p 48 14 6 p 62 1 62 pges x 6 6 P Haushalt A Haushalt B 12 Angebot von C 7 3 x1 3,5 x2 x 1+x 2 Nachfrage b) Zeichnen Sie zusätzlich die Angebotskurve von C in das Diagramm. Bei welchem Preis und bei welcher Menge ist der Markt für W-Männer im Gleichgewicht? Laut der o.g. Liste besteht das Gleichgewicht bei einem Preis von 2€. An diesem Punkt werden 7 Einheiten W.-Männer von C angeboten, und 3 bzw. 4 W.-Männer von den beiden Haushalten nachgefragt. ??????????????????Konrad????????????????????? c) Nehmen Sie an, der Staat möchte sich besonders kinderfreundlich zeigen und begrenzt den Preis für W-Männer durch staatlichen Markteingriff auf maximal 1 Euro (staatlich festgelegter Höchstpreis). Erklären Sie die resultierende Marktsituation, die entsteht, wenn der Staat durch seinen Eingriff den Marktmechanismus außer Kraft setzt. Vergleichen Sie diese Situation mit der Gleichgewichts-Marktsituation unter b). In welchem Ausmaß sind die Nachfrage von A und B und in welchem Ausmaß das Angebot von C für die bei dem Höchstpreis von 1 Euro entstehende Knappheit verantwortlich? (Vgl Pindyck.Rubinfeld 2.7 ; Schumann IIIA3c. Bei p = 1 ergibt sich eine Knappheit in Höhe der Überschußnachfrage x -y = 8, die sich gegenüber dem Gleichgewicht aus Nachfrageausweitungen von A in Höhe von 4 und von B in Höhe von 2 und der Angebotseinschränkung von C in Höhe von 2 ermitteln läßt) d) Was wird in dieser Situation auf dem W-Mann-Markt mit dem Preis für SchokoladenKringel geschehen? (mit Begründung) e) Was spricht Ihrer Meinung nach für und was gegen diesen staatlichen Markteingriff? Frage 41 Erklären Sie die wesentlichen Entwicklungen auf dem Weltölmarkt der letzten 40 Jahre mit Hilfe von komparativ statischen Marktanalysen. ?????????????? Reicht das?? Frage 42 a) Der Preis für Brasilianischen Rohkaffee auf dem Kaffeemarkt weist im Zeitverlauf starke kurzfristige Preisschwankungen von bis zu 400 % auf, die sich mittel- und langfristig wieder auf normales Niveau zurückentwickeln. Dabei werden die Preiserhöhungen durch Dürre und Frost ausgelöst. Erläutern Sie die Zusammenhänge unter Berücksichtigung der unterschiedlichen Preiselastizitäten des Angebots und der Nachfrage für die kurze und für die lange Frist. Bei Verbrauchsgütern typisch: Kurzfristig kleine Preiselastizität Langfristig große Preiselastizität (kleine Wirkung) (große Wirkung) Beim Automarkt ist es anders: Kurzfristig große Preiselastizität (Erstmal bricht Nachfrage stark ein) Langfristig kleine Preiselastizität (wird dann aber wieder stärker) Hier fehlt noch was! b) Wie würden sich die obigen Zusammenhänge ändern, wenn Preiselastizität der KaffeeNachfrage hier sehr viel größer wäre als sie normalerweise ist? (Je ein Marktdiagramm für die kurze und eins für die lange Frist. Vgl. Pindyck/Rubinfeld S.78-80 Beispiel 2.6) ) Einscannen? Frage 43 a) Wodurch unterscheiden sich die beiden "Nutzengebirge" aus einer Nutzenfunktion U(x1,x2), - wenn gilt, daß U = 0 , falls x1 = 0 und x2 = 0 ? Das Gebirge fällt zu den Achsen hin immer bis auf Null ab! - wenn gilt, daß U = 0 , falls x1 = 0 oder x2 = 0 ? Dann fällt es nur zu einer Achse auf Null ab, über der anderen Achse kann immer noch ein Schnitt durch das Gebirge liegen. b) Erläutern Sie die oben auftretenden Unterschiede in der Nutzenbeurteilung der Güter. ??? c) Was versteht man unter dem Grenznutzen eines Wirtschaftssubjektes in Bezug auf ein Gut? In der Volkswirtschaft ist Grenznutzen eine Bezeichnung für den Nutzenzuwachs, der entsteht, wenn ein Verbraucher sein Verbrauchsniveau erhöht. d) Erläutern Sie mit einem Beispiel das sog. Gesetz des abnehmenden Grenznutzens (1. Gossen´sches Gesetz) mit einer Nutzenkurve (Grafik). Dem „Gesetz vom abnehmenden Grenznutzen” zufolge erhöht der Besitz zusätzlicher Güter die gesamte innere Zufriedenheit oder den Nutzen des Besitzers nur bis zu einem gewissen Grad. Der Gesamtnutzen steigt in geringerem Maß, da der Effekt des Konsums, die Befriedigung des Bedürfnisses, immer mehr abnimmt. 1. Gossen´sche Gesetz: Auch Gesetz der Bedürfnissättigung oder Gesetz vom abnehmenden Grenznutzen: „Die Größe ein und desselben Genusses nimmt, wenn wir mit der Bereitung des Genusses ununterbrochen fortfahren, fortwährend ab, bis zuletzt Sättigung eintritt.” Es kommt demnach nicht allein auf den absoluten Nutzen, sondern auch auf den Zuwachs an Nutzen an. Der Grenznutzen eines Gutes nimmt mit dem Wachstum der verfügbaren Menge dieses Gutes ab, je größer die verfügbare Menge eines Gutes ist, desto geringer ist der Anreiz, weitere Einheiten des Gutes zu nutzen. Bsp.: Salz in der Suppe U Abnehmender Grenznutzen x2 x1 e) Obwohl Trinkwasser lebenswichtiger ist als Diamanten, haben Diamanten normalerweise einen höheren Marktpreis. Erläutern Sie den Sachverhalt unter Berücksichtigung der unterschiedlichen Entwicklungen der Grenznutzen bei steigender Verfügbarkeit für beide Güter. Erst einmal gründet sich der hohe Preis von Diamanten auf ihre Seltenheit. Der Grenznutzen beschreibt den Nutzenzuwachs eines Gutes. Ein Mensch kann nicht unendlich viel Trinkwasser in sich aufnehmen, deshalb handelt es sich hierbei um einen abnehmenden Grenznutzen. Irgendwann nützt einem keine zusätzliche Einheit Wasser mehr etwas. U x1 2U f ´´1 2 x1 f ´´1 0 x2 x2 Abnehmender Grenznutzen x2 x1 Dies ist bei Diamanten jedoch anders. Hier handelt es sich um einen positiven Granznutzen. Jede weitere Einheit dieses Gutes erstellt einen Nutzenzuwachs, wenn dieser auch nach einem gewissen grad nur noch langsam zunimmt. Nutzen U x2 x2 Höherer Grenznutzen Pos. Grenznutzen x2 x1 Frage 44 a) Erläutern Sie den Begriff der `Indifferenzkurve´ unter Verwendung einer grafischen Darstellung in einem (x1, x2)-Diagramm. Niveaus Nutzenniveaus: Alles was drüber liegt ist besser, alles was drunter liegt ist schlechter. X1 B H D Indifferenzkurve (können sich nicht schneiden!) X2 Indifferenzkurven eines Individuums beschreiben Güterkombinationen mit dem gleichen Maß an Nutzen. Jeder Punkt auf der Kurve beschreibt eine dieser Kombinationen. Verschiedene Personen haben unterschiedliche Indifferenzkurven. Indifferenzkurven sind Schnitte durch ein Nutzengebirge. Indifference = Gleichgültigkeit Es ist egal, welche Kombination gewählt wird, weil sie alle den selben Effekt haben. b) Erläutern Sie den Begriff der `Grenzrate der Substitution´ (GRS) für einen Punkt auf der Indifferenzkurve. (grafische, algebraische und verbale Lösung) Die GRS beschreibt, wie viele Einheiten man von einem Gut x1 aufgeben muß, um 1 zusätzliche Einheit des Gutes x2 zu bekommen, ohne an Nutzen zu verlieren! Beispiel: Wenn es draußen kalt ist, ist man bereit vieles für eine warme Jacke aufzugeben, die GRS ist folglich sehr groß. Algebraische Herleitung: Tot. Diff.: dU f f dx1 dx2 x1 x2 dU 0 0 f1´dx1 f 2 ´dx 2 f 2 ´dx2 f1´dx1 Grenzrate der Substitution: dx1 f 2 ´ dx2 f1´ dx1 f´ 2 dx2 f1´ Graphische Herleitung: X1 dx1 Uo dx2 X2 c) Leiten Sie den Zusammenhang zwischen der GRS und dem Verhältnis der Grenznutzen der beiden Güter algebraisch her. Hab ich das nicht da oben eben gemacht?? d) Für beide Güter möge jeweils das 1. Gossen´schen Gesetz gelten. Erläutern Sie, warum es danach entlang einer Indifferenzkurve zu sinkenden GRS kommt. (mit Grafiken). ?????????? d) Begründen Sie ökonomisch, warum Indifferenzkurven eine negative Steigung haben und warum Sie in der Regel konvex zum Ursprung gekrümmt sind. Indifferenzkurven sind die 2-dimensionale Betrachtung der Höhenlinien des Nutzengebirges. Die negative Steigung rührt aus dem allgemein negativen Zusammenhang zweier Güter bei beschränktem Einkommen. Wenn man von einem Gut eine Einheit mehr will, muss man dafür auf einen bestimmten Anteil des anderen Gutes verzichten (Volleinsatz der Ressourcen vorausgesetzt). Sie sind konvex, weil eine Güterkombination höheren Nutzen haben wird, als die Extremwerte. Daher muss die Nutzenkurve ein geringeres Mengenverhältnis haben. Frage 45 a) Erläutern Sie, auf welche drei Weisen eine Nutzenkurve für x1, eine Nutzenkurve für x2 und eine Indifferenzkurve jeweils als ein spezieller Schnitt durch das durch eine Nutzenfunktion gegebenen "Nutzengebirge" erzeugt werden kann. Zeichnung des Gebirges wäre Hilfreich Die Nutzenkurve für x1 bekommt man, indem man das Gebirge parallel zur x1-Achse bei einem konstanten x2 schneidet. Die Nutzenkurve für x2 erreicht man analog durch einen Schnitt paralell zur x2-Achse unter Beibehalten eines konstanten x1. Die Indifferenzkurve erhält man durch die Höhenlinie als Schnitt bei einem konstanten Nutzen U. b) Was genau bedeutet Transitivität der Präferenzen eines Wirtschaftssubjektes? Es handelt sich hierbei um eines der 3 Axiome bei der Bewertung verschiedener Möglichkeiten. Transitivität der Präferenzen bedeutet, die Möglichkeiten einer Wahl sind widerspruchsfrei und konsistent. Frage 46 Zeichnen Sie die speziellen Indifferenzkurven (Skizze des jeweils typischen Verlaufes) für die folgenden Präferenzen: a) HH A ist der Auffassung, daß Gut 1 restlos durch Gut 2 ersetzt werden kann aber Gut 2 nicht restlos durch Gut 1 ersetzt werden kann (Gut 2 ist nicht vollständig substituierbar). Weiß nicht wie…. b) HH B isst einen Hamburger und spült ihn mit einem Bier herunter. Ohne eine weitere Einheit des einen Gutes wird er keine weitere Einheit des anderen Gutes konsumieren. c) Hund Bello mag Wurst, interessiert sich aber nicht für Fisch. Skizzieren Sie seine Indifferenzkurven. d) Kühlaggregate sind durch ein bestimmtes Verhältnis der Eigenschaften "Kühlleistung" und "Lärmerzeugung" gekennzeichnet. Wie könnten die Indifferenzkurven (Iso-Nutzenlinien) eines Käufers von Kühlaggregaten aussehen? Frage 47 Was bedeutet es ökonomisch genau, a) - wenn ein HH sich auf einer bestimmten gegebenen Indifferenzkurve nach links oben bewegt? Die Güterkombination verändert sich! Der HH verwendet mehr von Gut x1 u weniger von x2, zieht aber immer noch den gleichen Nutzen aus seinem Warenkorb. b) - wenn ein HH von einem Punkt auf einer gegebenen Indifferenzkurve auf einen Punkt einer andere Indifferenzkurve wechselt, die näher zum Koordinatennullpunkt liegt? Der HH wechselt auf ein niedriger gelegenes Nutzenniveau. Dieses ist ein schlechteres, denn es werden sowohl weniger Einheiten des Gutes x1 als auch des Gutes x2 erhalten. Dies kann in einem niedrigeren Einkommen, oder höheren Preisen der Güter begründet liegen. c) - wenn der HH über längere Zeit eine bestimmte Güterversorgung beibehält, während das System aller Indifferenzkurven des HH sich insgesamt in dieser Zeit vom Koordinatennullpunkt weg verschiebt? (Beachten Sie, daß in diesem Falle eine gegebene Güterversorgung auf einer neuen Indifferenzkurve liegt!) Das ist mir zu hoch! Frage 48 Nehmen Sie an, ein HH sieht Jever und Astra als vollkommene Substitute an, die er, unabhängig von seinen Versorgungsniveaus, immer genau im Verhältnis 1:1 substituiert, ohne Nutzeneinbußen zu erleiden. a) Zeichnen Sie eine Schar von Indifferenzkurven, die diese Präferenzen des HH beschreiben. Astra Vollständige Substitution realisierbar In verschiedenen Versorgungsniveaus Indifferenzkurven Jever b) Was versteht man unter der Grenzrate der Substitution? Wie groß ist sie im obigen Beispiel? Die GRS beschreibt, wie viele Einheiten man von einem Gut x1 aufgeben muss, um 1 zusätzliche Einheit des Gutes x2 zu bekommen, ohne an Nutzen zu verlieren! Im obigen Beispiel ist die GRS genau 1, denn da es sich um vollständige Substitute handelt, und wir davon ausgehen, dass beide Biere den gleichen Preis haben, muss der HH genau ein Astra aufgeben, um ein Jever mehr kaufen zu können! c) Welchen optimalen Warenkorb aus Jever und Astra wird der HH mit einem Budget von Euro 20,- wählen, wenn 1 Flasche Jever Euro 2,- kostet und 1 Flasche Astra Euro 1,- ? (Grafische Analyse der nutzenmaximalen Konsumentscheidung). ( Dies ist ein Sonderfall, das Optimum ist hier kein Tangentialpunkt von Budgetgerade und Indifferenzkurve : Es handelt sich um eine Randlösung, bei der die Marginalbedingung nicht gilt : 20 Flaschen Astra) Bitte überprüfen! Wenn Jever und Astra dem HH wirklich gleich gut schmecken, dann wäre es nur logisch alle 20 € nur für Astra auszugeben, denn dann bekommt man die größte Menge Pivo für sein Geld! „Dat sach ich dir!“ (Dittsche) Astra Theoretischer Tangentialpunkt ??????? 0 Jever Frage 49 a) Untersuchen Sie mit Hilfe der 1. und 2. partiellen Ableitungen nach x1 und nach x2 , ob die Nutzenfunktion U = 0,8x10,3x20,6 für Gut 1 und für Gut 2 einerseits positive und andererseits abnehmende Grenznutzen aufweist. U f ´1 x1 Positiver Grenznutzen: f ´1 0 2U f ´´1 2 x1 Abnehmender Grenznutzen U 0 , 7 0,6 f1´ 0,24 x1 x2 x1 f ´´1 0 2U 0, 6 f1´´ 0,168 x11,7 x2 2 x1 Auswertung bzgl. pos. oder neg. / zunehmend oder abnehmend? U 0,3 0 , 4 f 2 ´ 0,8 x1 0,6 x2 x2 2U 1, 4 f 2 ´´ 0,8 x10,3 (0,24) x2 2 x2 Auswertung bzgl. pos. oder neg. / zunehmend oder abnehmend? b) Welches Vorzeichen hat hier d2U/(dx1dx2) ? 2U 1, 7 1, 4 f ´´ 0,168 x1 (0,24) x2 Ist das so gemeint? Dann wäre es ein pos. Vorzeichen. x2 x1 Welche Bedeutung hat dies für die Zeichnung von zwei Nutzenkurven von x1 für ein gegebenes Niveau x2 = 10 und für ein anderes gegebenes Niveau x2 = 15 ? (Zeichnung) (Berechnung der Ableitungen und Untersuchung ihrer Vorzeichen. Unterstellen Sie, dass: x1, x2 >= 0) Das ist eher was für dich , glaub ich! Frage 50 a) Erläutern Sie, warum im Haushaltsoptimum eines HH seine individuelle GRS |dx1/dx2| gerade so groß sein muss, wie die Opportunitätskosten des Konsums einer zusätzlichen Einheit von Gut 2 bei den herrschenden Marktpreisen. (Herleitung der Optimalbedingung mit dem Lagrange-Ansatz und Interpretation) Da war ich schon weg! b) Einem HH mit der Nutzenfunktion U = x12 x2 steht eine Konsumsumme von e = 120 zur Verfügung. Die Güterpreise seien p1 = 4 und p2 = 2. Bestimmen Sie den optimalen Verbrauchsplan des HH und sein erreichbares Nutzenniveau. (x1* = 20 ; x2* = 20; U* = 8000) c) Bestimmen Sie die Grenzrate der Substitution von Gut 1 durch Gut 2 im Optimum. Erläutern Sie Ihren Ansatz. ( GRS = 1/2 ) d) Nehmen Sie an, die Konsumsumme und die beiden Preise fallen jeweils um 50 %. Welchen Einfluß hat das auf den optimalen Verbrauchsplan, das erreichbare Nutzenniveau und die Grenzrate der Substitution? (x1* = 20 ; x2* = 20; U* = 8000 ;Berechnung und Ergebniserläuterung) Frage 51 Ein HH befindet sich in einem bestimmten Punkt PO auf seiner Budgetgeraden und stellt in dieser Situation mit Erstaunen fest, daß seine Grenzrate der Substitution von Gut 1 durch Gut 2 in diesem Punkt wesentlich größer ist als das mengenmäßige Tauschverhältnis dieser Güter auf dem Gütermarkt (p2/p1). a) Erläutern Sie unter Verwendung der Begriffe "GRS" und "Opportunitätskosten", woran der HH den oben genannten Unterschied erkennen kann. dx1 p 2 dx2 p1 Im HH-Optimum muss gelten GRS (Steigung der Nutzenfkt.) = Tauschverhältnis der Güter. b) Untersuchen Sie, ob sich der HH gerade in seinem Optimum befindet, links davon oder rechts davon? (mit Zeichnung) c) Wie wird der HH sich vernünftigerweise verhalten, wenn er den oben genannten Unterschied erkennt, aber nicht weiss, wo genau sein Optimum liegt? Frage 52 a) Worin liegt der Unterschied zwischen ordinalen Nutzen und kardinalen Nutzen? Früher: Kardinale Nutzentheorie Gossen(1833)&Marshall(1898) Die Differenz zwischen zwei Niveaus ist durch eine messbare Zahl auszudrücken Heute: Ordinale Nutzentheorie Pareto (1906) Es gibt nur „Besser“, „Schlechter“ oder „Gleich“ b) Zeichnen Sie jeweils eine typische Indifferenzkurve für den Fall zweier substitutiver Güter, den Fall zweier komplementäter Güter, den Fall zweier neutraler (völlig unabhängiger) Güter und den Fall eines Gutes 1 mit positivem Nutzen und eines Gutes 2 mit negativem Nutzen (sog. "Ungut"). Erläutern Sie die Kurvenverläufe und geben Sie jeweils ein praktisches Beispiel. Gut 1 Substitutive Güter: Falls der Preis für ein Gut steigen sollte, nimmt man das andere. Bsp.: Erdgas und Erdöl Gut 2 Gut 1 Komplementäre Güter: Wenn der Preis für Gut 1 steigt, konsumiert man auch weniger von Gut 2. Bsp.: Benzin und Autos Gut 2 Gut 1 Neutrale Güter: Konsum steht in keinem Zusammenhang. ???????????????????????? Gut 2 Gut 1 Gut 1 : pos. Nutzen Gut 2 : neg. Nutzen ????????????????????????? Gut 2 Frage 53 Erläutern Sie das 1. Gossen´sche Gesetz. Auch Gesetz der Bedürfnissättigung oder Gesetz vom abnehmenden Grenznutzen: „Die Größe ein und desselben Genusses nimmt, wenn wir mit der Bereitung des Genusses ununterbrochen fortfahren, fortwährend ab, bis zuletzt Sättigung eintritt.” Es kommt demnach nicht allein auf den absoluten Nutzen, sondern auch auf den Zuwachs an Nutzen an. Der Grenznutzen eines Gutes nimmt mit dem Wachstum der verfügbaren Menge dieses Gutes ab, je größer die verfügbare Menge eines Gutes ist, desto geringer ist der Anreiz, weitere Einheiten des Gutes zu nutzen. Frage 54 a) Erläutern Sie kurz die wichtigsten Axiome, die bei Aufstellung Präferenzordnung erfüllt sein sollten: Vollständigkeit, Transitivität(Widerspruchsfreiheit), Monotonität(Nichtsättigung), Konvexität (sinkende GRS .Gütermischung wird gegenüber einseitigen Güterversorgungen vorgezogen) A) Alternativen sind vollständig B) Präferenzen sind transitiv (widerspruchsfrei ; konistent) C) Alle Güter sind nützlich ; Es gilt Nichtsättigung; A) AB ; BA ; A B = „wird vorgezogen vor“ = alternativ, hat den gleichen Nutzen wie (…) Steaks Hamburger Konsument kauft trotzdem Hamburger B) BMW Merzedes Merzedes Golf BMW Golf Axiome der Präferenzen: ordinale Vergleichbarkeit: x1x2 x1 wird x2 vorgezogen x1x2 x1 ist gleichgeschätzt zu x2 Vollständigkeit: alle Guter müssen eingeordnet sein Reflexibilität: keine Bündeldifferenz=Güter sind gleich Transitivität: x1x2 und x2x3 x1x3 Nichtsättigung: x1=x2+1Einheit x2x1 Substituierbarkeit: keine lexikographische Ordnung Konvexität: x1x2 Rationale Konsumente legen ihre Präferenzen nach diesen Axiomen fest b) Erläutern Sie mit einem Beispiel, welche Probleme für die rationale Wahlentscheidung eines Konsumenten entstehen, wenn er die einzelnen Güter nicht transitiv ordnet. Eine Verkettung von Alternativen kann zu Widersprüchen führen, die dann gegen das 2. Axiom der Transitivität (Widerspruchsfreiheit) verstoßen. Diese Alternativen unterschreiten in diesem Fall die Fühlbarkeitsschwelle. Fühlbarkeitsschwelle: Alpen Nordsee A N + 1€ A + 2€ N + 1€ […] A + 1000€ N + 999€ Verkettung führt zu Widerspruch A A + 1000€ Einzelne Alternativen unterschreiten die Fühlbarkeitsschwelle. Frage 55 Die Präferenzordnungen von vier HH lassen sich durch folgende Nutzenfunktionen beschreiben: 1) U = x1.x2 2) U = x12.x22 3) U = x12 + x22 4) U = Min (x1, x2) Min ist jeweils das Minimum der beiden Werte von x1 und x2. a) Zeichnen Sie für jede Nutzenfunktion den typischen Verlauf einer ausgewählten Indifferenzkurve in ein (x1,x2)-Gütermengendiagramm. (Auflösen nach x1 unter der Annahme eines konstanten Nutzenniveaus). U 1 x1 x2 x1 X1 U x2 U 2 x12 x22 x1 X1 X2 U x22 U 3 x12 x22 x1 U x22 X1 X2 X2 U4 = ????????? b) Welche dieser Präferenzordnungen entsprechen nicht den üblichen KonvexitätsAnnahmen? U3 entspricht nicht den Konvexitätsannahmen, weil die Grenzrate der Substitution nicht gilt. Extreme haben höheren Nutzen; -Gütermischung ist schlechter Frage 56 Gehen Sie von einem 2-Güter-Fall aus. Zeigen Sie algebraisch, daß die Summe der einzelnen Einkommenselastizitäten, jeweils gewichtet mit dem relativen Anteil des betreffenden Gutes an den Gesamtausgaben, immer gleich 1 ist. Was bedeutet im 2-Güter-Fall dieser Sachverhalt für das Gut 2, wenn es sich bei dem Gut 1 um ein superiores Gut handelt? (Hinweis: Budgetgleichung total differenzieren, wobei die Güterpreise hier konstant sind. Dann beide Seiten durch die Einkommensänderung de teilen, so daß die linke Seite gleich eins wird. Die Ausdrücke rechts so anordnen, daß die Einkommenselastizitäten und die Gewichte erkennbar werden. Wenn bei einer Einkommenssteigerung von 1 % die Nachfrage nach dem superioren Gut 1 zB um 2 % steigt, dann wird ein größerer Einkommensanteil für Gut 1 verbraucht als vorher; der Einkommensanteil für Gut 2 muss also sinken, Gut 2 ist hier notwendigerweise ein absolut inferiores Gut. Achtung: Dieser Zusammenhang gilt nur im 2-Güter-Fall!) Wieder was für dich, mein kleines Mathe AS! Das machst du doch mit Augen zu! Frage 57 Die Präferenzordnung eines HH sei beschrieben durch die Nutzenfunktion U = x11/2.x21/4 . Die Güterpreise seien p1 = 12 und p2 = 12 . a) Berechnen Sie die nutzenmaximalen Verbrauchsmengen für eine Konsumsumme e von Euro 180,-. (x1 = 10 ; x2 = 5) b) Wie verändern sich die Verbrauchsmengen im Haushaltsoptimum, wenn der Staat jedem Verbraucher für Gut 2 pro Gütereinheit eine Beihilfe (Preissubvention) von Euro 6,- je ME zahlt? ( der Verbraucher zahlt jetzt also wg der Subvention für Gut 2 nur noch p2 = 6). ( x1 = 10 ; x2 = 10 ) c) Wie hoch ist der insgesamt vom Staat zu zahlende Subventionsbetrag? ( Euro 60 : Optimale Verbrauchsmenge für Gut 2 mal Subventionsbetrag) d) Wie würde sich die Güternachfrage im HH-Optimum verändern, wenn der Staat dem HH den Subventionsbetrag aus c) nicht als Preissubvention gewährt hätte, sondern ihm einen gleich großen Betrag als pauschale Einkommenshilfe (allgemeine Einkommenssubvention) zukommen lassen würde? ( e = 240 x1 = 13,33 ; x2 = 6,67 ) d) Untersuchen Sie, welche Art der Subventionierung der HH hier vorziehen wird. (Einsetzen der Lösungen in die Nutzenfunktion : U(10;10) < U(13,33 ; 6,66) Der HH zieht die pauschale Einkommenshilfe der Preisbeihilfe vor.) Frage 58 a) Zeigen Sie, wie sich für stufenweise steigendes Einkommen e1< e2< e3 .... bei gegebenen, unveränderten Güterpreisen eine Folge von verschiedenen Haushaltsgleichgewichtspunkten im x1-x2-Diagramm grafisch herleiten lassen. (Gleichgewichtspunkte des HH : hier Punkte der sog. Einkommens-Konsum-Kurve) (Zeichnung mit vollständiger Bezeichnung aller Kurven und relevanten Punkte). b) Die Nutzenfunktion eines Nachfragers sei mit U = x11/8x23/8 gegeben, die Güterpreise seien p1 = 2 und p2 = 3 . Ermitteln Sie den Einfluß des Einkommensniveaus e auf die Nachfragemenge nach Gut 1 und Gut 2, wenn der Nachfrager bei jedem Einkommen jeweils seinen optimalen Konsumpunkt wählt. (Bestimmen Sie die nutzenmaximalen Verbrauchsmengen unter der Nebenbedingung e = 2x1 + 3x2 für ein allgemeines Einkommensniveau e: x1 = (1/8) e ; x2 = (1/4) e ) c) Wie groß sind hier die Einkommenselastizitäten? (Elastizitäten sind jeweils gleich 1). Engel-Kurven Frage 59 a) Zeigen Sie, wie sich bei schrittweiser Zunahme des Preises für Gut 1 1 p1 < 2p1 < 3p1 ....eine Folge von Haushaltsgleichgewichten im x1-x2-Diagramm grafisch herleiten lassen, wobei das Einkommen e und der Preis p2 sich nicht verändern. (Gleichgewichtspunkte des HH : hier Punkte der sog. Preis-Konsum-Kurve) (Zeichnung mit vollständiger Bezeichnung aller Kurven und relevanten Punkte) b) Die Nutzenfunktion des HH sei wie oben wiederum U = x11/8 x23/8 , das Einkommen e= 100 und p2 = 3. Ermitteln Sie den Einfluß des Preisniveaus p1 auf die Nachfrage des HH für das Gut 1, wenn der HH jeweils seinen optimalen Konsumpunkt wählt. (Bestimmen Sie die nutzenmaximalen Verbrauchsmenge für Gut 1 unter der Nebenbedingung 100 = p1 x1 + 3x2 für ein allgemeines Preisniveau p1 :x1 = 25 p1 bzw p1 = 25/x1 ) b) Wie groß ist hier die Preiselastizität der Güternachfrage in Bezug auf den eigenen Preis? (Gut 1: -1) Marshall-Kurven Frage 60 Wie groß ist die GRS für ein Güterverhältnis von 1:1 auf einer beliebigen Indifferenzkurve der Nutzenfunktion U = 6x10,4x20,8 ? (GRS = 2) Grenzrate der Substitution: dx1 f ´ 2 dx2 f1´ dx1 f ´ 6 x 0,8 x 0, 2 2 1 0,6 2 0,8 2 Mit der Annahme von x2 x1 dx2 f1´ 2,4 x1 x2 0, 4 Frage 61 Diskutieren Sie die sog. Fühlbarkeitsschwellen als eine mögliche Ursache für die Unfähigkeit eines Konsumenten, alle Güter transitiv zu ordnen. (Beispiel). Frage 62 Erläutern Sie mit Hilfe einer grafischen Darstellung, warum die Annahme falsch ist, Indifferenzkurven könnten sich schneiden.(Bezug zu den Axiomen der Präferenzordnungen herstellen) e A Karl ` B C Karl Güternachfrage Nein, Indifferenzkurven können sich nicht schneiden, weil: AB A C Transitivität: B C Das stimmt aber nicht! (s.Skizze) B hat mehr von x2 als von x2! BC Ringförmige Präferenzen: (Verletzung der Transitivität) BMW Benz GolfBMW Frage 63 a) Die Nutzenfunktion des HH sei wiederum U = x11/8 x23/8 und das Einkommen e= 100 . Leiten Sie die Preis-Nachfrage-Kurven (Marshall-Kurven) des HH für das Gut 1 und das Gut 2 her. ( p1 = 25/x1 ; p2 = 75/x2 ) b) Wie groß sind hier die Preiselastizitäten der Güternachfrage in Bezug auf ihren eigenen Preis? (Gut 1: -1 ; Gut 2: -1) c) Bestimmen Sie die Kreuzpreiselastizitäten für Gut 1 und für Gut 2 und prüfen Sie, ob der HH die beiden Güter eventuell als Substitute oder als Komplemente ansieht. (Güter werden als unabhängig voneinander angesehen) d) Untersuchen Sie, welchen Anteil seines Einkommens (p.x/e) der HH in diesem besonderen Beispiel jeweils für Gut 1 und für Gut 2 ausgibt. (Durch Berechnung des Optimums für beliebige Preise und Einkommenshöhen erhält man: Gut 1:25% und Gut 2: 75% des Einkommens. Die Einkommensanteile der Güter sind in diesem Beispiel unabhängig von der Höhe des Einkommens und unabhängig von der Höhe der Güter-Preise ) Frage 64 a) Gegeben seien die Preise p1 und p2 sowie das Einkommen e. Leiten Sie für eine Nutzenfunktion vom Cobb-Douglas-Typ U = x1a. x2b mit den festen Koeffizienten a,b>0 nach Lagrange das Haushaltsoptimum her und bestimmen Sie daraus die Güternachfragefunktionen des HH für x1 und für x2.. (Bestimmung der Bedingungen 1. Ordnung für ein Nutzenmaximum; Einsetzen in die Budgetgleichung und Auflösen nach x1 bzw x2. Sie erhalten hoffentlich folgende Ergebnisse: x1 = (e/p1)(a/(a+b)) und x2 = (e/p2)(b/(a+b)) Beachten Sie: Diese Ergebnisse gelten nur für den Sonderfall einer C-D-Nutzenfunktion!!! b) Erläutern Sie die Auswirkungen von Änderungen von e auf x1 und auf x2. Wie groß sind hier die Einkommenselastizitiäten der Nachfrage bei x1 und bei x2 ? c) Erläutern Sie die Auswirkungen von Änderungen von p1 auf x1 und von p2 auf p2. Wie groß sind jeweils die Preiselastizitäten der Nachfrage in Bezug auf den eigenen Preis? d) Wie groß sind die Kreuzpreiselastizitäten von p2 auf x1 und von p1 auf x2? Frage 65 Zeigen Sie, daß für allgemeine p1, p2 und e aus den drei unterschiedlichen Nutzenfunktionen a, b und c jeweils identische Nachfragefunktionen für Gut 1 einerseits und für Gut 2 andererseits herleitbar sind. a) U = x1 . x2 b) U = (x1 x2)0,5 c) U = ln x1 + ln x2 Frage 66 Drei HWI-Studenten I, II und III leben in einer Wohngemeinschaft und entscheiden demokratisch über die Anschaffung eines gemeinsamen Weihnachtsbaumes. Zur Auswahl stehen: eine Nordmann-Tanne (N), beliebt wegen ihrer Haltbarkeit, eine Korea-Tanne (K) mit bekanntlich ziemlich kurzen und weichen Nadeln und die besonders preisgünstige Blau-Fichte (B). Die Präferenzen der Studenten sind: I N>K>B II K>B>N III B>N>K Erläutern Sie, welche Probleme bei der Ermittlung einer gemeinsamen Präferenzordnung durch demokratische Abstimmung auftreten können. (Condorcet/Arrow-Paradox) Frage 67 Ein Fußballfan verwendet jedes Jahr 100 Euro für die beiden Güter "Bier" und "HSVEintrittskarten". Der Preis für 1 Bier ist 2 Euro, der Preis für eine Eintrittskarte ist 20 Euro. a) Zeichnen Sie die exakte Budgetgerade in ein Bier-HSV-Mengen-Diagramm. Wie gross sind die Opportunitätskosten eines zusätzlichen HSV-Spiels? Wie verläuft die neue Budgetlinie genau, b) -wenn der Fan für 3 Spiele persönlich einlösbare Freikarten bekommt, die nicht weiterverkäuflich sind? c) -wenn der Fan statt dessen für 30 Biere persönlich einlösbare Freigutscheine bekommt, die nicht weiterverkäuflich sind? d) -wenn er sowohl 3 Spielfreikarten als auch 30 Biergutscheine zur persönlichen Einlösung bekommt? e) -wenn er sowohl 3 Spielfreikarten als auch 30 Biergutscheine bekommt, die er selber verwenden oder auch verkaufen kann? Unter welchen speziellen Bedingungen könnte diese Möglichkeit zum Verkauf der Freikarten und der Gutscheine das optimale Verhalten des nutzenmaximierenden Fans gegenüber der Situation in (d) verändern? (Wenn seine GRS sehr gross oder aber sehr klein ist, wird der Fan sein Verhalten verändern: Grafik) f) Der Fan sieht Bier und HSV-Spiele als vollkommene Substitute an, seine GRS sei überall gleich 12. Zeichnen Sie eine Schar von seinen Indifferenzkurven. g) Ermitteln Sie zeichnerisch den jeweils optimalen Konsumpunkt des Fan für die Situationen (a), (b), (c), (d), (e). Warum gelten die üblichen Optimalitätsbedingungen hier nicht? (a: 0;5 b: 0;8 c: 30;5 d: 30:8 e: 0;11 Es handelt sich um Randlösungen). Frage 68 a) Beschreiben Sie das allgemeine Haushaltsoptimum mit Hilfe einer Grafik. b) Erläutern Sie das Konzept des "Grenznutzens des Geldes in alternativen Verwendungen". U = f(x1,x 2 ) Totales Differential : dU = f f dx1 + dx 2 x1 x 2 Indifferenzkurve dU = 0 : 0 = f1´dx1 + f2´dx 2 -f1´dx1 = f2´dx 2 dx1 f´ =- 2 dx 2 f1´ GRS dx1 f2´ = dx 2 f1´ Grenznutzen 2 = Grenznutzen 1 Anhand der obigen Berechnung sieht man, dass die GRS gleich dem umgekehrten Verhältnis der entsprechenden Grenznutzen ist. c) Warum befindet sich ein HH nicht im Optimum, wenn er bei sich unterschiedliche Grenznutzen des Geldes für die beiden Güter feststellt? Unterschiedliche Grenznutzen des Geldes haben immer eine Ausgleichssubstituition zur Folge. Ist der Nutzen einer zusätzlichen Einheit von Gut 1 größer, als der Nutzen einer zusätzlichen Einheit von Gut 2, so wird man die nächste auszugebende Geldeinheit für das Gut mit dem höheren zusätzlichen Nutzen ausgeben. d) Wo genau befindet sich der HH auf der Budgetgerade, wenn sein Grenznutzen des Geldes in der Verwendung für Gut 1 größer ist als in der Verwendung für Gut 2? Was wird der HH in dieser Situation zweckmäßigerweise tun? (mit ausführlicher Begründung) Ist der Grenznutzen für Gut 1 größer als für Gut 2, so substituiert der HH hin zu Gut 1. Daraus folgt, dass er sich auf der Budgetgeraden rechts vom Optimum befindet. Frage 69 Erläutern Sie das 2. Gossen`sche Gesetz mit Hilfe der "Grenznutzen des Geldes in alternativen Verwendungen". Die Bedingung für das HH – Optimum wird als das zweite Gossen´sche Gesetz f´ f´ bezeichnet und lautet: 2 = 1 . p2 p1 Die Aussage des 2. Gossen´schen Gesetzes ist einfach die, dass ein rationaler HH bei der Verausgabung seines Einkommens ein Güterbündel anstrebt, bei dem der für die verschiedenen Güter jeweils zuletzt ausgegebene € in allen Verwendungen den gleichen Nutzenzuwachs erzielt. Denn wenn dies noch nicht der Fall ist, dann ist es durch eine Umschichtung der Ausgaben noch möglich, das Nutzenniveau zu steigern, ohne mehr Geld ausgeben zu müssen. Anders ausgedrückt bedeutet es folgendes: U UE x1 ME Grenznutzen einer zusätzlichen Mengeneinheit x1 = p1 Preis in Geldeinheiten für eine Mengeneinheit € ME = Grenznutzen einer zusätzlichen für Gut 1ausgegebenen Geldeinheit "Grenznutzen des Geldes in der Verwendung für Gut 1". Im Optimum muss der Grenznutzen des Geldes für alle Güter gleich sein. Frage 70 Erläutern Sie, was man unter dem Sonderfall eines Giffen-Gutes versteht und zeigen Sie,wie die Preis-Nachfrage-Kurve eines Giffen-Gutes verläuft. Wie verläuft die zugrunde liegende Preis-Konsum-Kurve der Optimalpunkte, wenn eines der beiden Güter ein Giffen-Gut ist? (mit 2 Grafiken) Wenn die Marshallkurve folgendermaßen aussieht, spricht man von dem Giffen – Paradoxon: p und x steigen gleichzeitig p1 x1 Frage 71 a) Zeigen Sie, wie sich der Gesamteffekt einer Erhöhung des Güterpreises p1 nach Hicks in einen Substitutionseffekt (bei Nutzenstabilisierung, also entlang einer gegebenen Indifferenzkurve) und einen Einkommenseffekt zerlegen läßt. Führen Sie dazu als Zwischenschritt eine fiktive Budgetgerade ein, die bereits die Steigung des neuen Preisverhältnisses aufweist, aber noch die alte Indifferenzkurve tangiert.( Grafische Analyse im (x1,x2)-Diagramm mit ausführlichem Kommentar). Bei Preisänderungen kann man zwei unterschiedliche theoretische Aspekte beobachten: - den Einkommenseffekt nach Hick´s - den Substitutionseffekt (Nutzen – Stabilisierte Substitution) Ein Einkommenseffekt liegt vor, wenn z.B. der Preis für Gut 1 fällt, wodurch die Kaufkraft steigt, dieses entspricht dem Einkommenseffekt. Wenn nun z.B. der Preis für Gut 1 fällt und der Preis für Gut 2 konstant bleibt, verschiebt sich der HH in Richtung des Gutes 1, das ist der Substitutionseffekt. b) Diskutieren Sie die Wirkungsrichtung des Substitutionseffekts und die Wirkungsrichtung des Einkommenseffekts der unterstellten Preiserhöhung bei Gut 1 auf die Nachfragemenge von Gut 1. Welche Schlußfolgerungen lassen daraus für die Wirkungsrichtung des Gesamteffekts der Preissenkung auf die Nachfragemenge von Gut 1 ziehen? Zusatzfrage: Wie sehen Substitutionseffekt und Einkommenseffekt der unterstellten Preiserhöhung bei Gut 1 auf die Nachfragemenge von Gut 2 aus? c) Woran würde man bei der Analyse des Substitutionseffekts und des Einkommenseffekts erkennen, ob es sich bei dem untersuchten Gut um ein Giffen-Gut handeln könnte? d) Erklären Sie, warum jedes Giffen-Gut immer ein absolut inferiores Gut sein muß, nicht aber jedes absolut inferiore Gut ein Giffen-Gut sein muß. (Ausführlicher Lösungshinweis zu 71d: Zeichnen Sie in ein (x1,x2)-Diagramm für einen steigenden Preis von Gut 1 das alte Gleichgewicht (Punkt A) und das neue HH-Gleichgewicht (Punkt C) für den Fall, daß Gut 1 ein Giffen-Gut ist. Punkt C muß dann auf der flacheren neuen Budgetgerade links und oberhalb von Punkt A auf der alten Budgetgerade liegen. Nun zeichnen Sie den Punkt B ein, der auf der ursprünglichen Indifferenzkurve beim neuen Preisverhältnis liegt. Punkt B liegt damit rechts und unterhalb von Punkt A auf einer gemeinsamen Indifferezkurve.. Damit es zum Giffen-Paradox kommt, muss der Substitutionseffekt der Preisänderung (hier Abnahme der Nachfrage nach dem teuer gewordenen Gut 1 von Ordinatenwert von A auf Ordinatenwert von B) durch einen entgegen gerichteten Einkommenseffekt der Preisänderung (hier Zunahme der Nachfrage nach Gut 1 von Ordinatenwert B auf Ordinatenwert C) überkompensiert werden. Damit der Einkommenseffekt dem Substitutionseffekt entgegen gerichtet ist, muss die durch Preiserhöhung bewirkte Kaufkraftsenkung (wirkt wie eine Einkommenssenkung) hier zu einer Zunahme (!!!) der Nachfrage nach Gut 1 führen. Das kann nur geschehen, wenn es sich um ein absolut inferiores Gut handelt. Daher muss jedes Giffen-Gut immer ein absolut inferiores Gut sein. Andererseits könnte Gut 1 zwar ein absolut inferiores Gut sein, aber der (hier positive) Einkommenseffekt könnte absolut kleiner sein als der (hier negative) Substitutionseffekt. Dann gäbe es keine Überkompensation, der Punkt C würde dann zwar höher liegen als B aber doch noch niedriger als A. Man erkennt, dass nicht jedes absolut inferiore Gut ein Giffen-Gut sein muss. Wenn die Inferiorität nicht ausgeprägt genug ist, kann auch ein absolut inferiores Gut eine normale negative Preiselastizität der Nachfrage aufweisen. Vergl. Schumann, IB4d, Pindyck/Rubinfeld 4.2) Frage 72 a) Ein HH ißt nur Käse und Cracker und verwendet dafür sein gesamtes Budget. Erläutern Sie, ob Käse und Cracker für den HH beide superiore Güter sein können. b) Nehmen Sie an, Käse sei für den HH ein superiores Gut, während Cracker ein inferiores Gut ist. Was passiert mit dem Käse-Konsum des HH, wenn der Preis für Käse fällt? Was geschieht gleichzeitig mit dem Cracker-Verbrauch, wenn der Preis für Käse fällt? Begründen Sie Ihre Antworten unter Verwendung einer grafischen Analyse, in der die Gesamteffekte der Preissenkung für Käse auf die Nachfrage nach Käse und auf die Nachfrage nach Crackern jeweils in einen Substitutionseffekt und in einen Einkommenseffekt für Käse und einen Substitutionseffekt und einen Einkommenseffekt für Cracker zerlegt werden!!! Frage 73 Die Auswirkung der Änderung eines Güterpreises auf die Nachfragemenge kann nach Hicks in einen Substitutionseffekt und einen Einkommenseffekt zerlegt werden. Führen Sie diese Zerlegung zeichnerisch getrennt in jeweils einem x1-x2-Diagramm(!!!) durch (bitte Effekte deutlich erkennbar herausarbeiten) und kommentieren Sie die einzelnen Schritte a) für den Fall, daß Gut 1 billiger wird. b) für den Fall, daß Gut 2 billiger wird. c) für den Fall, daß Gut 2 teurer wird. (Hinweis: Man sollte diese Zerlegung unbedingt einmal für jeden der vier Fälle zeichnen. Zeichnen Sie zunächst immer die fiktive Budgetgerade und den Substitutionseffekt entlang der alten Indifferenzkurve und dann den Einkommenseffekt mit der Parallelverschiebung zur neuen Indifferenzkurve. Den Fall, daß Gut 1 teurer wird, haben wir bereits in Aufgabe 71 abgehandelt) Frage 74 Sie haben in der Frage 57d) für einen konkreten Fall untersucht, ob der HH eine Preissubvention oder eine gleich große pauschale Zahlung (Einkommenssubvention) vorzieht. Versuchen Sie in einem (x1-x2 )-Diagramm mit einer grafischen Analyse darzustellen, warum ein beliebiger HH im allgemeinen Fall immer eine pauschale Zahlung des Subventionsbetrages einer Preissubvention vorziehen wird. (Bei gleichen Subventions-Kosten für den Staat). Frage 75 Peters Grenzrate der Substitution von Orangensaft zu Apfelsaft sei immer gleichbleibend, ohne Rücksicht darauf, wie viel Orangensaft er trinkt. a) Zeichnen und erläutern Sie für einen variablen Preis des Apfelsafts die Preis-Konsumkurve und die Marshall-Kurve für Apfelsaft. b) Zeichnen und erläutern Sie für variables Einkommen eine Einkommens-Konsumkurve und eine Engel-Kurve für Apfelsaft. Frage 76 Wie verlaufen die Einkommens-Konsum-Kurve und die beiden Engel-Kurven, wenn Sie bei gegebenen Preisen p1 = 2,5 und p2 = 5 die folgenden Nutzenfunktionen unterstellen: U = 6x10,4x20,8 ( Berechnung der Kurvengleichungen) Untersuchen Sie, ob eins der beiden Güter inferior ist. Frage 77 Drei Vermögensverwalter A , B und C berücksichtigen in ihrer jeweiligen Nutzenfunktion U zum einen den erwarteten Ertrag ew und zum anderen das Risiko s einer Anlage U = U(ew,s) Aus dieser besonderen Nutzenfunktion lassen sich spezielle Indifferenzkurven für den erwarteten Etrag und das Risiko herleiten. Dabei geht man genau so vor, wie bei der Ermittlung der bisher behandelten Güter-Indifferenzkurven. Für alle drei Anleger gilt: dU/dew > 0 und U(ew, 0) > 0 für alle ew > 0 Entwickeln und erläutern Sie in jeweils einem ew-s-Diagramm den typischen Verlauf der Indifferenzkurven a) für den risiko-abgeneigten Anleger A mit dU/ds < 0 (Risiko ist ein "Nicht-Gut") b) für den risiko-neutralen Anleger B mit dU/ds =0 (Risiko ist ein "neutrales" Gut) c) und für den risiko-freundlichen Anleger C mit dU/ds > 0 (Risiko ist ein "Gut") (jede Indifferenzkurve beginnt an der Ordinatenachse (s =0) und verläuft mit zunehmendem s für A steigend (Risiko ist ein negatives "Gut") , für B horizontal (Risiko ist nutzenneutral) und für C fallend (Risiko ist hat positiven Nutzen) .Bedenken Sie, daß alle Punkte auf einer Indifferenzkurve gleichen Nutzen haben: Wenn C zb. bei gleich hohem ew einen Punkt mit höherem s dem Punkt mit niedrigerem s vorzieht, muß dieser Punkt auf einer höherenIndifferenzkurve liegen: dh. seine Indifferenzkurven verlaufend fallend. d) Unterstellen Sie, die Anleger können bei der Anlage ihres gegebenen Vermögens wählen zwischen einer sicheren Anlage mit ew = 0 und s = 0 (zb Kassenhaltung) und einer riskanten Anlage in ein Wertpapier mit ew = 100 und s = 100 sowie allen Kombinationen zwischen diesen beiden extremen Anlagen. Zeichnen Sie die Portfolio-Möglichkeitskurve (Portfolio-Budgetlinie) aller durch Mischung dieser Anlagen erreichbaren ew-s-Kombinationen für die Gesamt-Anlage in ein ew-sDiagramm. A, B und C wählen jeweils ihre optimale Anlagekombination auf der PortfolioMöglichkeitskurve mit ihrem maximalen Nutzen. Wodurch unterscheiden sich die Anlagen von A, B und C? (3 Grafiken mit Kennzeichnung des optimalen Anlagepunktes) e) Erläutern Sie (Diagramm) , wie sich das Anlageverhalten eines leicht risikoaversen Anlegers ändert, wenn für das Wertpapier in der Zukunft mit einem deutlich höherem ew zu rechnen ist, ohne dass sich seine Streuung s vergrößert. Frage 78 Drei Haushalte A, B und entscheiden über ihre Güternachfrage nicht unabhängig von anderen HH, sondern machen ihr individuelles Verhalten auch vom Verhalten der Mit-Konsumenten abhängig. Man spricht von sog. externen Konsum-Effekten (networl externalities) A unterliegt dem Mitläufer-Effekt und folgt den herrschenden Moden, B unterliegt dem SnobEffekt und liebt die Exklusivität und C unterliegt dem Prestige-Effekt (Veblen-Effekt) und beeindruckt gerne durch den Besitz sehr teurer Güter. Erläutern Sie das Verhalten der drei HH und geben Sie jeweils ein praktisches Beispiel für ein solches Verhalten. Überlegen Sie, wie sich die Preis-Nachfrage-Kurven modifizieren, wenn man die oben genannten Nachfrageinterdependenzen berücksichtigt. Wie verändert sich danach die Preiselastizität der Nachfrage für A, B und C? (A: wird absolut größer; B: wird absolut geringer; C: kann bei sehr großem Prestige-Effekt sogar positiv werden. Vergl. Schumann IB7e Nachfrageinterdependenzen; Pindyck/Rubinfeld 4.5) Externe Konsumeffekte (Netzwerk – Externalität) 1. Mitläufereffekt (P/R Seite 193) Eine positive Netzwerkexternalität, bei der ein Konsument ein Gut teilweise deshalb besitzen will, weil andere es besitzen. externerEffekt X1HH1 = X1HH1 (p1 ,p2 ,eHH1 , X1AlleHH ) - 2. Snob – Effekt + + + (P/R Seite 195) Negative Netzwerkexternalität, bei der der Konsument ein exklusives oder einzigartiges Gut besitzen will. externerEffekt HH1 1 X HH1 1 =X HH1 (p1 ,p2 ,e - , X1AlleHH ) + + - 3. Prestige – Effekt (Veblen – Effekt) externer Effekt HH1 1 X HH1 1 =X HH1 (p1 ,p2 ,e - + + , "p1" ) + Der Prestige – Effekt wird bei Ruiz auch „Porsche – Effekt“ genannt. Frage 79 a) Erläutern Sie die Problematik, das gängige ordinale Nutzenkonzept mit einer reellen Nutzenfunktion darzustellen. b) Was versteht man unter einer monotonen Transformation einer Nutzenfunktion, geben Sie für U= x1x2 fünf Beispiele für monotone Transformationen. c) Welche beiden der drei HH aus Frage 55 haben im Sinne des ordinalen Nutzenkonzepts die gleiche Präferenzordnung? (Erläutern Sie Ihre Untersuchungsmethode) (HH1 und HH2) d) Was ist der Unterschied zwischen einer Indifferenzkurve und einer Isoquante? Eine Isoquante ist eine Kurve, die alle möglichen Inputkombinationen darstellt, mit denen der gleiche Output erzielt werden kann. e) Erläutern Sie mit Hilfe einer grafischen Darstellung, warum Isoquanten fallend verlaufen. Frage 80 Ein HWI-Student verwendet jeden Monat einen Betrag von e zum Kauf von Gut 1 (Getränke) und von Gut 2 (Studien-Lehrbücher) mit den gegebenen Preisen p1 und p2. a) Erläutern Sie mit einer Grafik, wie sich die optimale Güternachfrage des Studenten verändert, wenn seine Eltern ihm bei jedem gekauften Lehrbuch die Hälfte des Preises dazugeben. Unterscheiden Sie dabei den Substitutionseffekt und den Einkommenseffekt dieser Maßnahme. b) Mit welcher grafik-basierten Analyse könnte der Student den Eltern seinen "Verbesserungsvorschlag" erläutern, daß es für ihn doch deutlich nützlicher wäre, wenn er die Beihilfe der Eltern einfach zur freien Verfügung bekommen könnte, ohne daß die Eltern auch nur einen Cent mehr zahlen müßten als vorher. Ermitteln Sie dazu in einer Zeichnung den Bereich, in dem der neue Konsumpunkt unter diesen Umständen liegen würde und untersuchen Sie die für den Studenten erreichbaren Nutzenniveaus. c) Welche Rolle spielt der Grad der Indifferenzkurvenkonvexität für die durch diesen "Verbesserungvorschlag" ausgelöste Größenordnung der Güternachfrageänderung? d) Was könnten die Eltern dagegen zur Rechtfertigung ihrer speziellen Buch-Subvention ins Feld führen? Wie werden Sie den Substitutionseffekt bewerten? Frage 81 - Was beschreibt eine Produktionsfunktion y = g(r1 , r2) genau? Die Produktionsfunktion hat im Allgemeinen die folgende Gestalt: y = g( r1,r2 Prod.menge ). Produktionsfaktoren Die Produktionsfunktion befasst sich mit der „Technik“. Des weiteren gibt es noch die Kostenfunktion, die die „Technik und die Ökonomie“ verbindet, woraus sich dann der optimale Produktionsplan ergibt. Die Produktionsfunktion kann kurzfristig in fixe und variable Produktionsfaktoren unterteilt werden. Es gibt formale Ähnlichkeiten zwischen der Theorie des HH und der der Unternehmung, aber Achtung sie sind inhaltlich zu unterscheiden. - Was bedeuten dabei die verwendeten Variablen, in welchen Dimensionen werden sie jeweils gemessen? y = g( r1,r2 Prod.menge ) Produktionsfaktoren - Was macht den Unterschied zwischen variablen und fixen Produktionsfaktoren aus? - Was versteht man unter einem Ertragsgebirge, und wie sieht es aus (Zeichnung)? - Wie ermittelt man aus einem Ertragsgebirge eine Ertragskurve für den Faktor 1? - Wie ermittelt man aus einem Ertragsgebirge eine Isoquante? Schnitt durch das Ertragsgebirge parallel zur x1 x2 Ebene. - Wie verlaufen die Ertragskurve und die Grenzertragskurve für den Faktor 1 ? (Zeichnung und Diskussion der Eigenschaften) die Ertragskurve und die Grenzertragskurve für den Faktor 2 ? (Zeichnung und Diskussion der Eigenschaften) -Welche Bedeutung hat eine Vergrößerung des Faktors 2 für die Ertragskurve von Faktor 1? -Geben Sie ein praktisches Beispiel für die Gültigkeit des sog. Ertragsgesetzes! Frage 82 In einem Unternehmen mit gegebener Maschinenausstattung produziert jeder zusätzliche Arbeiter bis zum sechsten Arbeiter (einschließlich) eine zusätzliche Outputeinheit. Jeder weitere Arbeiter vom siebten Arbeiter an produziert keinen zusätzlichen Output mehr Zeichnen Sie die Ertragskurve des Faktors Arbeit, die Kurve der durchschnittlichen Arbeitsproduktivität und die Grenzproduktivitätskurve für Arbeit.. Frage 83 a) Erläutern Sie die Begriffe "Isoquante" und "Grenzrate der Technischen Substitution" GRTS in einem (r1,r2)-Diagramm. Isoquanten r1 z.B. Arbeitnehmer dr1 dr 2 y = 110 y = 105 r2 z.B. Maschinen Eine Isoquante ist eine Kurve, die alle möglichen Inputkombinationen darstellt, mit denen der gleiche Output erzielt werden kann. Die obige Form der Isoquanten gilt für Substitutionale Produktionsfunktionen. Das sind Funktionen bei denen dieselbe Produktionsmenge mit unterschiedlichen Faktormengeneinsätzen erreichbar ist. dr1 . Die GRTS ist definiert als dr2 das betragsmäßige Verhältnis der Faktormengenänderungen bei konstantem Ertragsniveau. Die GRTS wird bei einer Bewegung entlang der Isoquanten von links oben nach rechts unten immer kleiner, dieses wird als das Gesetz von der abnehmenden Grenzrate der Faktorsubstitution bezeichnet. Die Grenzrate der technischen Substitution GRTS = b) Zeigen Sie, daß sich die GRTS auf das Verhältnis der Grenzproduktivitäten der Güter zurückführen läßt. (Produktionsfunktion total differenzieren; dy = 0) Aus y = g(r1,r2 ) wird das Totale Differential gebildet : dy = g1' dr1 + g'2dr2 . Desweiteren muss auf einer Isoquanten gelten dy = 0. Damit ergibt sich 0 = g1' dr1 + g'2dr2 . dr1 g'2 Daraus folgt schließlich = . dr2 g1' c) Bei r1 = 4 und r2 = 3 ist dy/dr1 = 2 und dy/dr2 = 3. Wie groß ist hier die GRTS? d) Was versteht man unter einer substitutionalen Produktionsfunktion, was unter einer limitationalen Produktionsfunktion und wodurch unterscheiden sich ihre jeweiligen Isoquanten? (Zeichnung) Leontief – Produktionsfunktion / limitationale Produktionsfunktion Eine Produktionsfunktion bei der eine Substitution der Produktionsfaktoren aufgrund technischer Gegebenheiten völlig unmöglich ist, bezeichnet man als Leontief – Produktionsfunktion . Zwischen der Produktion und dem jeweiligen Faktoreinsatz besteht ein festes Verhältnis. Folgend ist ein Isoquanten – Bild einer Leontief – Produktionsfunktion dargestellt: r1 y2 y1 y0 r2 r1 z.B. Arbeitnehmer dr1 dr 2 y = 110 y = 105 r2 z.B. Maschinen Die obige Form der Isoquanten gilt für Substitutionale Produktionsfunktionen. Das sind Funktionen bei denen dieselbe Produktionsmenge mit unterschiedlichen Faktormengeneinsätzen erreichbar ist. e) Welche Punkte auf den Isoquanten einer limitationalen Produktionsfunktion sind keine effizienten Produktionspunkte? (Begründung) f) Wie sehen die Ertragskurven und Grenzertragskurven für die Faktoren bei einer limitationalen Produktionsfunktion aus? (Der Grenzertrag einer Vergrößerung nur eines Faktors ist gleich Null) g) Diskutieren Sie, warum die GRTS entlang einer Isoquante aus einer substitutionalen Produktionsfunktion normalerweise mit Zunahme von r2 sinkt. Die GRTS wird bei einer Bewegung entlang der Isoquanten von links oben nach rechts unten immer kleiner, dieses wird als das Gesetz von der abnehmenden Grenzrate der Faktorsubstitution bezeichnet. Frage 84 Gegeben sei die Produktionsfunktion y = 1,2r10,4r20,3 (y Output; r1 und r2 Faktoreinsatzmengen) a) Untersuchen Sie algebraisch, ob beide Produktionsfaktoren positive Grenzerträge aufweisen und ob sie beide auch sinkende Grenzerträge aufweisen. Erläutern Sie die folgenden Eigenschaften: "Faktoren sind unbegrenzt produktiv" ; Es gilt das "Gesetz abnehmender Grenzprodukte". b) Erläutern Sie allgemein, was man unter dem Homogenitätsgrad m einer beliebigen Produktionsfunktion versteht.(mit algebraischer Darstellung) Homogenitätsgrad berechnen: y = r1αr21-α k m y = k αr1αk1-αr21-α = k1r1αr21-α = k1y Homogenitätsgrad m =1. c) Untersuchen Sie algebraisch, ob die obige Produktionsfunktion homogen ist und welchen Homogenitätsgrad sie gegebenenfalls aufweist. (Funktion ist homogen vom Grade m=0,7) d) Erläutern Sie denkbare ökonomische Ursachen in der Praxis für das Auftreten steigender Skalenerträge der Produktion oder das Auftreten sinkender Skalenerträge der Produktion . Allgemein gilt: m<1 m>1 sinkende Skalenerträge steigende Skalenerträge Sinkende Skalenerträge bedeutet, dass sich die Isoquanten immer weiter aneinander nähern, je größer die Produktionsmenge y wird. Steigende Skalenerträge bedeutet, dass sich die Isoquanten immer weiter voneinander entfernen, je größer die Produktionsmenge y wird. e) Skizzieren Sie die relative Position folgender ausgewählter Isoquanten dieser Produktionsfunktion: Zeichnen Sie die vier Isoquanten für die folgenden Produktionsniveaus: y1 = 1 ; y2 = 2; y3 = 3; y4 = 4 . (Keine genaue Berechnung erforderlich, die Funktionseigenschaft soll aber grafisch klar erkennbar sein) Betrachten Sie 4 andere Isoquanten der oben genannten Produktionsfunktion, die im (x1-x2)Diagramm jeweils einen gleichen Abstand zu einander aufweisen, weil sie jeweils Punkte mit der einfachen, doppelten, dreifachen oder vierfachen Menge beider Faktoren enthalten. Berechnen Sie die zu diesen Isoquanten gehörigen Produktionsniveaus! (wenn y1 = 1 : y2 = 1,62 ; y3 = 2,16 ; y4 = 2,64 ) Frage 85 Gegeben sei eine andere Produktionsfunktion y = 0,2r11,4r20,5 (y Output; r1 und r2 Faktoreinsatzmengen) Untersuchen Sie auch diese Funktion algebraisch, ob beide Produktionsfaktoren positive Grenzerträge aufweisen und ob sie beide auch sinkende Grenzerträge aufweisen und untersuchen Sie zusätzlich, ob die obige Produktionsfunktion homogen ist und welchen Homogenitätsgrad sie gegebenenfalls aufweist. Frage 86 Prüfen Sie folgende Produktionsfunktionen auf Homogenität und ermitteln Sie gegebenenfalls den Homogenitätsgrad. (1) y = 0,8r11/4 + 0,7r23/4 (nicht-homogen) (2) y = 0,5r10,4r20,6 (homogen vom Grade 1, linear-homogen) (3) y = (r1r2/(r1 + r2))3/2 (homogen vom Grade 1,5) (4) y = 0,8r10,5r20,6 (homogen vom Grade 1,1) 0,4 0,4 (5) y = 0,4r1 + r2 (homogen vom Grade 0,4) Frage 87 a) Ist es möglich, daß bei einem Produktionsprozess einerseits sinkende Grenzerträge der Faktoren und andererseits gleichzeitig steigende Skalenerträge (Homogenitätsgrad m > 1) auftreten können? Wie müßte das Ertragsgebirge in solch einem Falle aussehen? b) Untersuchen Sie die Produktionsfunktion y = 0,8r10,5 r20,75darauf hin! Frage 88 Die Produktionskosten K eines Unternehmens sind in folgender Definitionsgleichung mit K = r1.q1 + r2.q2 + F gegeben. ( r1, r2 verwendete Faktormengen. q1,q2 Faktorpreise. F Fixkosten der Produktion ) a) Zeichnen Sie für einen gegebenen festen Kostenbetrag K0 die dabei möglichen Faktormengenkombinationen von r1 und r2 in ein (r1-r2)-Diagramm und erläutern Sie, was die Achsenabschnitte und was die Steigung dieser sogenannten Isokostengerade festlegt. b) Wie verändert sich die Kurve bei Verdoppelung des Kostenbetrages, wenn alles andere gleich bleibt? c) Zeigen Sie unter Berücksichtigung der Isoquanten, wie man für gegebene Kosten K0 die maximale Produktion geometrisch finden kann. d) Gehen Sie alternativ von einer gegebenen Produktionshöhe y0 aus. Zeigen Sie, wie man für diese gegebene Produktion den Produktionspunkt mit den minimalen Produktionskosten geometrisch finden kann. Frage 89 a) Unterstellen Sie die folgende "typische" Kostenfunktion K(y) = ay3 + by2 +cy + F für die Kosten K in Abhängigkeit von der Produktionsmenge y (feste Parameter a,c > 0 ; b < 0 ; F Fixkosten) und fertigen Sie eine Skizze des Verlaufs. b) Erläutern Sie die Eigenschaften der hinter einer solchen typischen Kostenfunktion stehenden Produktionsfunktion. Die Faktorpreise für r1 und r2 seien mit q1 und q2 gegeben. Erläutern Sie das Auftreten von konstanten Skalenerträgen, steigenden Skalenerträgen oder sinkenden Skalenerträgen für die vermutliche Entwicklung der Produktionskosten in Abhängigkeit von der Produktionsmenge y. c) Ermitteln Sie aus der obigen Funktion die folgenden, aus der BWL bekannten speziellen Kosten algebraisch: Fixkosten pro Stück (Durchschnittliche Fixkosten DF), variable Kosten pro Stück (DVK), totale Kosten pro Stück (DTK) und die Grenzkosten (GK). d) Zeichnen Sie Verläufe dieser Kosten in ein Kosten-Produktionsmengen-Diagramm. e) Zeigen und erklären Sie, warum die GK-Kurve immer durch die Minima der DTK-Kurve und der DVK-Kurve laufen muß. Frage 90 Ein Unternehmen produziert unter Verwendung zweier variabler Faktoren r1 und r2 mit den gegebenen Faktorpreisen q1 = 1 und q2 = 16 und mit der folgenden Produktionsfunktion, deren Kenntnis für die Berechnung der Kosten unbedingt erforderlich ist: Y = r10,5 + r20,5 . Die Fixkosten betragen F = 50 Euro. a) Zeigen Sie, wie sich die verschiedenen Mininalkostenkombinationen geometrisch ermitteln lassen. b) Ermitteln Sie die kostenminimieren Faktoreinsatzverhältnisse für verschiedene y-Niveaus. (Minimieren Sie dazu die Kosten unter der Nebenbedingung, daß die Produktion mit der gegebenen Produktionsfunktion erfolgt). ( r1* = 256 r2* ) c) Ermitteln Sie die Gesamtkostenfunktion K = K(y). ( K = 0,941y2 + 50 ) (Durch Einsetzen des kostenminimalen Faktoreinsatzverhältnisses in die Produktionsfunktion, Ermittlung der kostenminimierenden Faktormengen als Funktion von y und Einsetzen in die Definitionsgleichung für Kosten.) d) Bestimmen Sie mit der ermittelten Kostenfunktion die gewinnmaximale Produktionsmenge des Unternehmens für einen gegebenen Güterpreis von Euro 18,82. (Aus der Bedingung für das Gewinnmaximum bei vollständiger Konkurrenz auf dem Gütermarkt) ( y* = 10 ) e) Wie groß sind in diesem Unternehmen bei gewinnmaximaler Produktionsmenge die Fixkosten pro Stück, die variablen Kosten pro Stück, die totalen Kosten pro Stück, die Grenzkosten, der Gewinn pro Stück und der Gesamtgewinn? ( DF = 5 , DVK = 9,41, DTK = 14,41, GK = 18,82 , G/y = 4,41, G = 44,10 ) Frage 91 a) Leiten Sie für ein Unternehmen bei vollständiger Konkurrenz auf seinen Güter- und Faktormärkten die Bedingungen für die gewinnmaximale Arbeitseinsatzmenge und für die gewinnmaximale Kapitaleinsatzmenge analytisch her (Inputregel). b) Erläutern Sie dazu die Begriffe "physisches Grenzprodukt der Arbeit" und "Wertgrenzprodukt der Arbeit", "physisches Grenzprodukt des Kapitals" und "Wertgrenzprodukt des Kapitals". (Vgl. Schumann, IID2, VB) Frage 92 Die Produktionsfaktoren werden im Gewinnmaximum bekanntlich jeweils in der Höhe ihres Wertgrenzproduktes entlohnt. (Inputregel) Unterstellen Sie die Produktionsfunktion y = r10,6 . r2 0,4 a) Untersuchen Sie die Funktion auf Homogenität und bestimmen Sie ggf. den Homogenitätsgrad. b) Berechnen Sie die sich ergebenden gewinnmaximalen Faktoreinkommen (bei vollständiger Konkurrenz auf allen Märkten) (Faktorpreis*Faktormenge) für r1 und für r2 mit gegebenen p (Güterpreis) und q1 , q2 (Faktorpreise) (q1 . r1 = p. 0,6.r1-0,4 . r2 0,4 .r1 q2 . r2 = p. 0,4. r10,6. r2-0,6 .r2 c) Zeigen Sie, daß bei dieser Produktionsfunktion der Erlös py im Gewinnmaximum gerade ausreicht, um die Summe der obigen Faktoreinkommen zu bezahlen und das Gewinnresiduum G daher gleich Null ist (Dies ist die Aussage des "Adding-up-Theorems" oder auch EulerTheorems für linear-homogene Produktionsfunktionen. ). c) In welchem Verhältnis wird der Erlös auf die Produktionsfaktoren aufgeteilt? ( 60% für Faktor 1, 40 % für Faktor 2; Die Verteilung ist durch die Parameter der Produktionsfunktion "technisch" festgelegt!!!) Frage 93 a) Ein Unternehmer plant, eine vorgegebene Produktionsmenge y* zu produzieren. Erläutern Sie in einem (r1,r2)-Diagramm, wo die Minimalkostenkombination des Unternehmers liegt. b) Wie wird der Unternehmer reagieren, wenn plötzlich der Preis q1 des Faktors 1, etwa der Preis für Energie cet. par. steigt, weil eine zusätzliche Energiesteuer erhoben wird? Wo liegt das neue Kostenminimum? Vergleichen Sie die Grenzrate der technischen Substitution im alten Kostenminimum mit der Grenzrate der Substitution im neuen Kostenminimum. (Die Grenzrate GRTS fällt, weil der Unternehmer entlang der Isoquante r1 durch r2 technisch subsituiert. Wiederholen Sie hierzu das Beispiel aus der Vorlesung mit der kostenminimierenden Reaktion eines Stahlwerks auf die Einführung von Abwassergebühren,, Vgl. Pindyck/Rubinfeld , S.321ff ,Beispiel 7.4 ) c) Unter welchen besonderen Bedingungen wird der Unternehmer nicht reagieren? d) Erläutern Sie mit Hilfe einer Grafik, wie sich bei konstantem Faktorpreisverhältnis aus den jeweiligen Minimalkostenkombinationen für unterschiedliche Produktionsmengen die sog. Faktoranpassungskurve zeichnerisch ermitteln läßt. e) Zeigen Sie algebraisch, daß die Faktoranpassungskurve mit Isoquanten aus einer CobbDouglas-Produktionsfunktion immer eine Gerade aus dem Ursprung sein muss. f) Erläutern Sie mit Hilfe einer Zeichnung, wie die spezielle Kostenfunktion K(y) einer homogenen Produktionsfunktion mit steigenden Skalenerträgen (Homogenitätsgrad m>1) aussieht. Erläutern mit ökonomischen Argumenten ihren speziellen Grenzkostenverlauf. Frage 94 a) Erläutern Sie die Begriffe "physisches Grenzprodukt der Arbeit" und "Wertgrenzprodukt der Arbeit" einerseits, "physisches Grenzprodukt des Kapitals" und "Wertgrenzprodukt des Kapitals" andererseits. b) Erläutern Sie, warum im Gewinnmaximum das Wertgrenzprodukt der Arbeit gleich dem Marktpreis für Arbeit q1 sein muss und das Wertgrenzprodukt des Kapitals gleich dem Marktpreis für Kapital q2 ? Zeigen Sie mit diesen Bedingungen, daß im Gewinnmaximum immer ein Kostenminimum vorliegt. c) Zeichnen Sie die gewinnmaximale Arbeitseinsatzmenge für einen gegebenen Güterpreis, einen gegebenen Preis für Arbeit und eine gegebenen Produktionsfunktion in eine Grafik. Warum ist die Wertgrenzproduktskurve gleichzeitig die Arbeitsnachfragekurve des gewinnmaximierenden Unternehmers? d) Zeigen Sie grafisch, welche Wirkungen es auf die gewinnmaximale Arbeitsnachfrage (bei gegebenem Kapitaleinsatz) hat, - wenn der Güterpreis p auf dem Absatzmarkt steigt (cet. par.). - wenn die Gewerkschaft einen steigenden Lohnsatz q1 auf dem Arbeitsmarkt durchsetzt (cet. par.) - wenn sich die Grenzproduktivität der Arbeitskräfte durch eine verbesserte Produktionstechnik generell erhöht. (cet. par) (Beachten Sie, daß es für diese Analysen nicht darauf ankommt, welche Ursachen die unterstellten Parameteränderungen haben.) e) Da die Löhne normalerweise einen nicht geringen Teil der Kosten ausmachen, trachtet der gewinnmaximierende Unternehmer gewöhnlich danach, die Löhne möglichst gering zu halten. Henry Ford hat dem gegenüber 1914 die Löhne für seine Arbeiter auf den doppelten Marktlohnsatz erhöht und dies als "eine der besten Maßnahmen zur Kostensenkung, die je durchgeführt wurde" bezeichnet. Erläutern Sie die der Maßnahme zugrunde liegende Idee des Effizienzlohns. Welche Wirkungen auf die gewinnmaximale Arbeitsnachfrage müssen bei einer Lohnerhöhung nach der Effizienzlohntheorie berücksichtigt werden? (Vgl. Pindyck/Rubinfeld Kap. 17.5,3) Frage 95 In Frage 90d haben Sie die gewinnmaximale Produktionsmenge eines Unternehmens nach der Outputregel ermittelt. a) Bestimmen Sie nun für das oben beschriebene Unternehmen die beiden (kurzfristigen) Faktornachfragefunktionen bei dem gegebenen Güterpreis p von Euro 18,82 und berechnen Sie daraus die gewinnmaximalen Faktoreinsatzmengen nach der Inputregel bei den auf den Faktormärkten gegebenen Preisen von q1 = 1 und q2 = 16. Welche Produktionsmenge wird mit den gewinnmaximalen Faktoreinsatzmengen produziert? ( q1 = 9,41r1-0,5 q2 = 9,41r2-0,5 r1* = 88,548 r2* = 0,3459 y* = 10, natürlich ) b) Ermitteln und zeichnen Sie für die Kostenfunktion aus Frage 90c die Güterangebotskurve eines gewinnmaximierenden Mengenanpassers. (Grafik) Frage 96 a) Erläutern Sie, was man unter einem Markt mit vollständiger Konkurrenz versteht. Wie groß ist hier der Einfluß der einzelnen Marktteilnehmer auf den Marktpreis? Wie groß wäre der Einfluß aller Marktteilnehmer zusammen auf den Marktpreis? b) Erläutern Sie mit Hilfe einer Grafik den Sonderfall, daß auf einem Markt kein Gleichgewicht existiert und geben Sie ein praktisches Beispiel dafür. c) Unterstellen Sie, daß sich die Preise auf einem anderen Markt zu einem eindeutigen Gleichgewichtspreis hin bewegen, wobei die Preis-Anpassung durch die Funktion F mit dem Argument (N-A) (Überschußnachfrage) beschrieben wird: dp/dt = F(N-A) mit F´ > 0 und F(0) = 0 . Erläutern Sie unter Verwendung einer Marktgrafik für ein konkretes Beispiel, durch welche Reaktionen der Anbieter und der Nachfrager es bei einem "zu hohen Preis" zu der oben beschriebenen Anpassung in Richtung Gleichgewicht kommt. d) Bei welchen Kurvenverläufen der Angebotskurve und der Nachfragekurve wäre ein Gleichgewicht nicht stabil? Frage 97 Zur wohlfahrtstheoretischen Bewertung der Funktionsweise von Märkten (Markteffizienz) kann das Konzept der "Konsumentenrente" , der "Produzentenrente" bzw der "Gesamtrente" herangezogen werden. a) Zeigen Sie in einer Grafik mit einer Nachfragekurve, wie man aus der individuellen Zahlungsbereitschaft und dem gezahlten Marktpreis die Konsumentenrente bestimmen kann. Welcher Konsument hat die größte Konsumentenrente, welcher Konsument die kleinste? b) Erklären Sie die Produzentenrente aus den Produktionskosten der Anbieter und dem tatsächlich erhaltenen Marktpreis. c) Zeigen Sie in einem Diagramm, wie bei vollständiger Konkurrenz im Marktgleichgewicht die Konsumentenrente, die Produzentenrente und die Gesamtrente bestimmt werden können. ( Vgl. Pindyck/Rubinfeld , Kap.9; Schumann, IIA2e.) Frage 98 a) Zeigen Sie mit Hilfe des Konzepts der Gesamtrente, daß das Marktergebnis bei freier Preisbildung auf einem Markt bei vollständiger Konkurrenz die Gesamtrenten (Wohlfahrt von Konsumenten und Produzenten) maximiert (Vorliegen von Markteffizienz) und damit unter dem Wohlfahrtsaspekt als gesellschaftlich besser zu beurteilen ist als andere Märkte, in denen der Staat in die Preisbildung eingreift. (Marktdiagramm) b) Untersuchen Sie in einem Marktdiagramm die veränderte Marktsituation auf einem Konkurrenzmarkt, wenn der Staat unterhalb des Gleichgewichtspreises einen Höchstpreis pMAX verbindlich festlegt. (Beispiel: Mietpreisspiegel in Hamburg) Analysieren Sie die Wirkungen eines solchen Eingriffs auf die Produzentenrente, die Konsumentenrente und auf die Gesamtrente und diskutieren Sie die Vorteile und Nachteile des Eingriffs gegenüber der freien Preisbildung für die einzelnen Wirtschaftssubjekte und für die Gesamtwirtschaft. Zeigen Sie, daß der durch pMAX entstehende Nachfrageüberhang durch einen Angebotsrückgang und durch gleichzeitige Nachfrageausweitung verursacht wird. c) Bei staatlicher Festsetzung eines über dem freien Gleichgewichtspreis liegenden Mindestpreises. pMIN läßt sich eine andere Marktsituation mit einem Angebotsüberhang entwickeln. (Grafische Lösung) (Beispiele: Agrarpreisstützung, um Produzenten vor starkem Preisverfall in der Folge von Angebotsschocks (Superernte) oder Nachfrageschocks (BSE-Diskussion) zu schützen.) Analysieren Sie die Wirkungen auch dieses Eingriffs auf die Produzentenrente, die Konsumentenrente und auf die Gesamtrente und diskutieren Sie die Vorteile und Nachteile des Eingriffs gegenüber der freien Preisbildung für die einzelnen Wirtschaftssubjekte und für die Gesamtwirtschaft,.wenn die Produzenten Ihr Angebot, abweichend von ihrer Angebotskurve, an die nachgefrage Menge bei pMIN anpassen? d) Welche Wirkung auf die Konsumentenrente, die Prozentenrente, die Staatskosten und Netto-Gesamtwohlfahrt hätte es im obigen Beispiel (c), wenn der Staat zusätzlich auf dem Markt zur Preisstützung als Nachfrager interveniert und durch staatliche Aufkäufe das gesamte Überschußangebot bei pMIN vom Markt nimmt und ans Ausland verschenkt? Wer hat durch die staatlichen Aufkäufe gegenüber (c) einen Vorteil, wer einen Nachteil? Frage 99 a) Auf dem amerikanischen Benzinmarkt war die Benzinnachfrage Mitte der 90ger Jahre mit x = 150 -50p gegeben und das Benzinangebot mit y = 60 + 40p (x,y in Milliarden Gallonen pro Jahr; p in $ pro Gallone) . Bestimmen Sie rechnerisch den Gleichgewichtspreis p* und die Gleichgewichtsmenge x* auf dem Markt und zeichnen Sie die Kurven in ein Marktdiagramm. (p* = 1,00; x* = 100) b) Berechnen Sie die Auswirkungen einer staatlichen Benzin-Steuer von t = 0,5 $ pro Gallone auf das Marktgleichgewicht. (x* = 89 , Gleichgewichtspreis der Nachfrager Np* = 1,22 ; Gleichgewichtspreis der Anbieter Ap* = 0,72) .c) Wie groß wird die Steuereinnahme des Staates sein, welchen Anteil der Steuerlast müssen die Konsumenten tragen und welchen Anteil tragen die Produzenten? ( tx* = 44,5 Milliarden $ , 19,58 Milliarden $ davon tragen die Konsumenten und 24,92 Milliarden $ die Anbieter). (Berücksichtigen Sie für Ihre Lösungen, dass auch nach der Einführung der Steuer im neuen Gleichgewicht x* = y* sein muss und dass die Nachfrager und die Anbieter den zu dieser Gleichgewichtsmenge gehörenden Preis auf ihrer jeweiligen Marktverhaltenskurve zahlen werden, wobei der von den Käufern zu zahlende Preis um den Steuerbetrag t größer sein muß als der Preis, den die Anbieter nach Abzug der Steuer erhalten.(Steuer-"Keil") Vgl. Pindyck/Rubinfeld, Beispiel 9.6, S451ff.) d) Zeichnen die Auswirkungen der Benzinsteuer in ein Marktdiagramm und untersuchen und diskutieren Sie die Auswirkungen der Steuer auf die Konsumentenrente, die Produzentenrente und die Rente des Staates. Warum ist der Wohlfahrtsverlust der Konsumenten und Produzenten größer als der Wohlfahrtsgewinn des Staates? Zeigen Sie, wie sich der daraus ergebende Nettowohlfahrtsverlust grafisch bestimmen läßt. Was bestimmt die Höhe dieses Verlustes? Frage 100 a) Zeigen Sie mit einer Grafik, daß die Auswirkung einer Steuer auf die Konsumentenrente und die Produzentenrente von der Preis-Elastizität des Angebotes und der Preiselastizität der Nachfrage abhängt. b) Wegen der auftretenden Abhängigkeit vom Nikotin ist es bekanntlich schwer, sich das Rauchen abzugewöhnen. Welche Folgerungen ergeben sich daraus für die Wirkung der Tabaksteuer auf die Konsumentenrente und den Anteil der Tabaksteuerlast, den die Raucher tragen müssen?. c) Der Staat plant durch eine Besteuerung von Segel-Yachten die wohlhabenden LuxusgutNachfrager an der Finanzierung der öffentlichen Haushalte zu beteiligen. Diese Steuer führt bekanntlich dazu, daß für die Nachfrager im Gleichgewicht bei der gehandelten Gleichgewichtsmenge ein um den Steuerbetrag höherer Preis auf der Nachfragekurve gilt als für die Anbieter bei der Gleichgewichtsmenge auf der Angebotskurve. Der Markt für Yachten ist durch eine hohe (negative) Preiselastizität der Nachfrage der wohlhabenden Kunden und durch eine niedrige (positive) Preiselastizität des Angebots der mittelständischen Werften gekennzeichnet. Erläutern Sie mit einer Grafik, wie sich ein solcher Staats-Eingriff durch Besteuerung im Yachten-Markt auf die Konsumentenrente, die Produzentenrente und auf die Gesamtrente (inklusive Steuereinnahmen) auswirken wird. Wer hat dadurch Vorteile, wer hat Nachteile? Wird das Ziel der Besteuerung erreicht? d) Wie Sie wissen, ist die Nachfrage nach dem dauerhaften Konsumgut PKW durch einen Bestandsanpassungsprozess gekennzeichnet. Nehmen Sie an, daß (wie in Dänemark) plötzlich eine spezielle Umsatzsteuer in Höhe von 100% auf PKW erhoben wird. Wird der von den Konsumenten getragenen Anteil der Steuer im Laufe der Zeit steigen oder sinken oder wird er gleich bleiben? Frage 101 a) Die Bedingung 1. Ordnung für ein Gewinnmaximum nach der Outputregel lautet bekanntlich E´(y) = K´(y) . Unter der Annahme der vollständigen Konkurrenz auf einem Markt stehen viele kleine Anbieter ohne Marktmacht einer Vielzahl von kleinen Nachfragern ohne Marktmacht gegenüber, der Grenzerlös eines kleinen Anbieters ist dann E´= p . Zeigen Sie, daß dagegen der Grenzerlös für einen großen Anbieter mit Marktmacht (etwa einem Monopolisten) immer kleiner ist als der Preis in der Ausgangslage, wobei es hier entscheidend auf die Höhe der jeweils relevanten Preiselastizität der Nachfrage Ex;p < 0 ankommt. ( Vergl. Schumann IID1; Herleitung und Interpretation von E´(y) = p (1 + 1/Ex,p) ) b) Ein großer Anbieter mit Marktmacht (Monopolist) hat die Kostenfunktion K = 0,75y2 + 4 und steht auf seinem Absatzmarkt folgender Nachfragefunktion gegenüber: p = -1,5y + 36 Berechnen Sie seine Erlösfunktion, seine Grenzerlösfunktion und seine Grenzkostenkurve und zeichnen Sie die Kurven in ein (p,y)-Marktdiagramm. Bei welchem y* ist die Bedingung 1.Ordung für sein Gewinnmaximum erfüllt und welchen Marktpreis p* werden die Nachfrager bei dem Angebot von y* zahlen? (y* = 8; p* = 24 ) c) Welcher Preis und welche Absatzmenge würde sich ergeben, wenn der Monopolist durch staatliche Kontrolle gezwungen würde, Preis und Menge so festzulegen, wie sie sich durch viele kleine Anbieter mit der gleichen Kostenfunktion auf einem Konkurrenzmarkt ergeben würden? (Die Güterangebotsfunktion auf dem Markt würde durch den steigenden Ast der Grenzkostenkurve bestimmt, bei der oben gegebenen Güternachfragefunktion ergibt sich: K´ = 1,5y p = -1,5y + 36 K´ = p !!! y** = 12 p** = 18.) d) Vergleichen Sie die Konkurrenzsituation (c) mit der Marktmachtsituation (b) im Hinblick auf die Konsumentenrente, die Produzentenrente und die Gesamtrente und diskutieren Sie auf dieser Grundlage die Vorteile bzw Nachteile einer Konkurrenzsituation gegenüber einer Monopolsituation für die Nachfrager, die Produzenten und für die Gesamtwirtschaft. (Vgl. Pindyck/Rubinfeld Abbild. 10.10 , S.491) *************************************************************************** *************** Allen Klausurteilnehmern wünsche ich viel Erfolg, alle übrigen Teilnehmern eine angenehme Semesterpause bis zur 1. Vorlesung Makroökonomie am 8.4.2004.
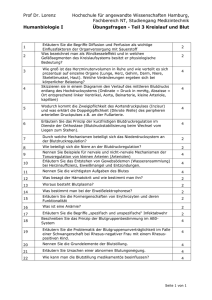




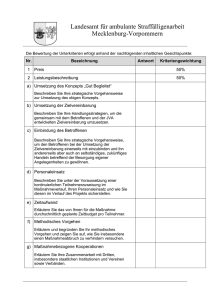

![Aufgabe 1 [ Markt und Marktinterventionen ] Das Streben nach](http://s1.studylibde.com/store/data/001810673_1-f17ea9e5378542d3ef29a2e698d95c40-300x300.png)