Prof

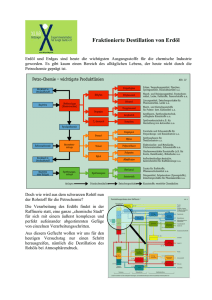
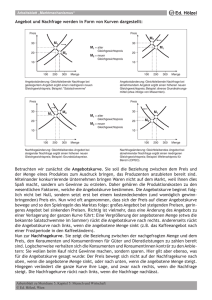
Prof. Dr. Rainer Marggraf
WS 2007/08
Vorlesung
Volkswirtschaftslehre
Übungsfragen
13. Das Angebot der Unternehmung
13.1 Severinus, der Krähenhändler, ist für seine Leberkräuter berühmt. Seine Gesamtkostenfunktion lautet c(y) = y2 + 10.
a) Wie lautet seine Grenzkostenfunktion? – Seine Durchschnittskostenfunktion?
b) Bei welcher Menge sind seine Grenzkosten gleich den Durchschnittskosten? – Bei
welcher Menge sind seine Durchschnittskosten ein Minimum?
c) Wie hoch muß auf einem Wettbewerbsmarkt der niedrigste Preis sein, zu dem er
eine positive Menge anbieten wird? – Wieviel würde er zu diesem Preis anbieten?
13.2 Die Raffinesse-Raffinerie wandelt Rohöl in Benzin um. Man benötigt zur Produktion
eines Fasses Benzin ein Faß Rohöl. Zusätzlich zum Rohöl entstehen bei der
Raffinierung auch noch andere Kosten. Die Erzeugung von y Fässern Benzin kann durch
die Kostenfunktion c(y) = y2/2 + p0y beschrieben werden, wobei p0 der Preis eines
Fasses Rohöl darstellt.
a) Drücke die Grenzkosten der Erzeugung von Benzin als eine Funktion von p0 und y
aus.
b) Angenommen die Raffinerie kann 50 Fässer Rohöl um $ 5 kaufen, sie muß jedoch
$ 15 für jedes Faß Rohöl zahlen, das sie über 50 hinausgehend kauft. Die
Grenzkostenkurve für Benzin wird daher bis zu einer Menge von 50 Fässern Benzin
............................... lauten und danach ....................................
c) Zeichnen Sie in ein Diagramm die Angebotskurve der Raffinesse-Raffinerie ein.
d) Angenommen die Raffinesse-Raffinerie sieht sich bei einem Preis von $ 30 je Faß
einer horizontalen Benzinnachfragekurve gegenüber. Zeichnen Sie diese
Nachfragekurve ein. – Wieviel Benzin wird die Raffinerie anbieten?
e) Nun kann die Raffinesse-Raffinerie die ersten 50 Fässer Rohöl nicht mehr um $ 5
kaufen, sondern muß für ihr gesamtes Rohöl $ 15 je Faß zahlen. Wie würde sich ihr
Output ändern?
14. Marktangebot einer Branche
14.1 Gegeben sei eine Branche unter vollständiger Konkurrenz mit einer großen Zahl von
Unternehmungen, die alle die identische Kostenfunktion c(y) = y2 + 1 haben. Die
Nachfragefunktion lautet D(p) = 55 – p.
a) Wie lautet die Angebotskurve einer einzelnen Unternehmung? – Wie lautet die
Angebotskurve der Branche, wenn sie aus n Unternehmungen besteht?
b) Wie hoch wird der Gleichgewichtspreis für n = 20 sein? – Wie groß wird der Output
jeder einzelnen Unternehmung im Gleichgewicht sein?
c) Wie groß wird der Gleichgewichtsoutput der gesamten Branche sein?
d) Wie groß werden die Gleichgewichtsgewinne jeder einzelnen Unternehmung sein?
e) Angenommen die Nachfrage verschiebt sich auf D(p) = 44 – p. Wie hoch wird der
neue Gleichgewichtspreis sein?
f) Wie groß wird der Output jeder einzelnen Unternehmung im Gleichgewicht sein? –
Wie groß werden die Gleichgewichtsgewinne jeder einzelnen Unternehmung sein?
14.2 In dieser Aufgabe wollen wir die landwirtschaftliche Nutzung von Land in der
Umgebung einer Stadt im Gleichgewicht ermitteln. Stellen wir uns eine Stadt vor, die in
der Mitte einer eher gesichtslosen Ebene liegt. Der Weizenpreis im Stadtzentrum beträgt
pro Zentner € 10, die Kosten für die Produktion eines Zentners Weizen betragen
lediglich € 5. Der Transport eines Zentners Weizen kostet pro Kilometer 10 Cent.
a) Schreiben Sie die Gleichung für den Gewinn einer Farm pro Zentner Weizen, den
sie zum Markt transportiert, wenn die Farm t Kilometer vom Stadtzentrum entfernt
ist.
b) Nehmen wir an, daß man auf einem Hektar Land 1.000 Zentner Weizen ernten kann.
Um wieviel wird man einen Hektar Land pachten können, der t Kilometer vom
Markt entfernt liegt?
c) Wie weit muß man vom Markt entfernt sein, damit das Land Null wert ist?
15. Monopol
15.1 Ein Monopolist sieht sich der inversen Nachfragekurve p(y) = 12 – y gegenüber, seine
Kostenkurve lautet c(y) = y2.
a) Wie hoch wird sein gewinnmaximierendes Outputniveau sein?
b) Angenommen der Staat besteuert den Monopolisten in der Form, daß er für jede
verkaufte Einheit € 2 an den Staat abführen muß. Wie hoch wird sein Output bei
dieser Art der Besteuerung sein?
c) Angenommen der Staat erhebt alternativ (zu b) eine Pauschalsteuer von € 10 auf den
Gewinn des Monopolisten. Wie hoch wird nun sein Output sein?