Partneraufgabe Name

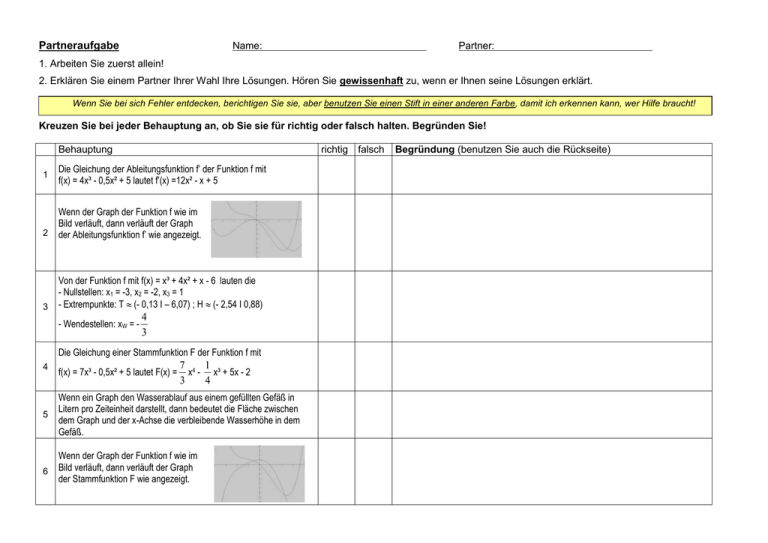
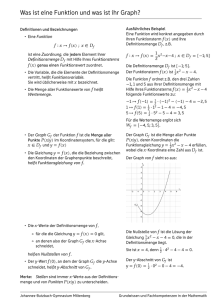
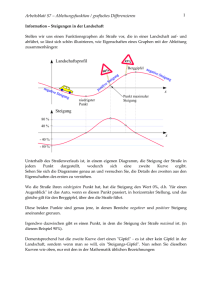
Partneraufgabe
Name:
Partner:
1. Arbeiten Sie zuerst allein!
2. Erklären Sie einem Partner Ihrer Wahl Ihre Lösungen. Hören Sie gewissenhaft zu, wenn er Ihnen seine Lösungen erklärt.
Wenn Sie bei sich Fehler entdecken, berichtigen Sie sie, aber benutzen Sie einen Stift in einer anderen Farbe, damit ich erkennen kann, wer Hilfe braucht!
Kreuzen Sie bei jeder Behauptung an, ob Sie sie für richtig oder falsch halten. Begründen Sie!
Behauptung
1
richtig falsch
Die Gleichung der Ableitungsfunktion f’ der Funktion f mit
f(x) = 4x³ - 0,5x² + 5 lautet f’(x) =12x² - x + 5
2
Wenn der Graph der Funktion f wie im
Bild verläuft, dann verläuft der Graph
der Ableitungsfunktion f’ wie angezeigt.
3
Von der Funktion f mit f(x) = x³ + 4x² + x - 6 lauten die
- Nullstellen: x1 = -3, x2 = -2, x3 = 1
- Extrempunkte: T  (- 0,13 I – 6,07) ; H  (- 2,54 I 0,88)
- Wendestellen: xW = -
4
3
Die Gleichung einer Stammfunktion F der Funktion f mit
7 4 1
x - x³ + 5x - 2
3
4
4
f(x) = 7x³ - 0,5x² + 5 lautet F(x) =
5
Wenn ein Graph den Wasserablauf aus einem gefüllten Gefäß in
Litern pro Zeiteinheit darstellt, dann bedeutet die Fläche zwischen
dem Graph und der x-Achse die verbleibende Wasserhöhe in dem
Gefäß.
6
Wenn der Graph der Funktion f wie im
Bild verläuft, dann verläuft der Graph
der Stammfunktion F wie angezeigt.
Begründung (benutzen Sie auch die Rückseite)
Partneraufgabe
Name:
Partner:
1. Arbeiten Sie zuerst allein!
2. Erklären Sie einem Partner Ihrer Wahl Ihre Lösungen. Hören Sie gewissenhaft zu, wenn er Ihnen seine Lösungen erklärt.
Wenn Sie bei sich Fehler entdecken, berichtigen Sie sie, aber benutzen Sie einen Stift in einer anderen Farbe, damit ich erkennen kann, wer Hilfe braucht!
Kreuzen Sie bei jeder Behauptung an, ob Sie sie für richtig oder falsch halten. Begründen Sie!
Behauptung
1
richtig falsch
Die Gleichung der Ableitungsfunktion f’ der Funktion f mit
f(x) = 4x³ - 0,5x² + 5 lautet f’(x) =12x² - x + 5
2
Wenn der Graph der Funktion f wie im
Bild verläuft, dann verläuft der Graph
der Ableitungsfunktion f’ wie angezeigt.
3
Von der Funktion f mit f(x) = x³ + 4x² + x - 6 lauten die
- Nullstellen: x1 = -3, x2 = -2, x3 = 1
- Extrempunkte: T  (- 0,13 I – 6,07) ; H  (- 2,54 I 0,88)
x
Begründung (benutzen Sie auch die Rückseite)
f’(x) =12x² - x (Ableitung des absoluten Gliedes ist 0)
x
x
Begründung durch Rechnung.
4
- Wendestellen: xW = 3
Die Gleichung einer Stammfunktion F der Funktion f mit
7 4 1
x - x³ + 5x - 2
3
4
4
f(x) = 7x³ - 0,5x² + 5 lautet F(x) =
5
Wenn ein Graph den Wasserablauf aus einem gefüllten Gefäß in
Litern pro Zeiteinheit darstellt, dann bedeutet die Fläche zwischen
dem Graph und der x-Achse die verbleibende Wasserhöhe in dem
Gefäß.
6
Wenn der Graph der Funktion f wie im
Bild verläuft, dann verläuft der Graph
der Stammfunktion F wie angezeigt.
x
7 4 1
x - x³ + 5x - 2
4
6
x
F(x) =
x
Menge des abgeflossenen Wassers
Begründung darüber, dass f das Steigungsverhalten von F beschreibt.