Übungsaufgaben - Institut für Medizinische Informatik

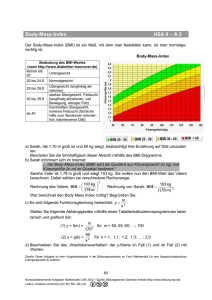
INSTITUT FÜR MEDIZINISCHE INFORMATIK, STATISTIK UND EPIDEMIOLOGIE
Statistik für Studenten der Sportwissenschaften
SS 2007
Aufgabe 1
Man weiß von Rehabilitanden, die sich einer bestimmten Gymnastik unterziehen, dass sie im
Mittel µ=54 Jahre (mit einer Standardabweichung von σ=3 Jahre) alt sind.
a) Welcher Anteil der Rehabilitanden ist
(1) Jünger als 48 Jahre?
(2) Älter als 63 Jahre?
(3) Zwischen 48 und 60 Jahren alt?
b) Bestimmen Sie das obere Quartil, d.h. die Altersgrenze, über der 25% aller Rehabilitanden liegen?
Aufgabe 2
Seit dem Giftgasunfall in Soveso hatten die der Dioxin-Belastung ausgesetzten Männer 88
Jungen und 103 Mädchen gezeugt. Die normale Geschlechtsverteilung ist 106:100. Ist das
ein signifikanter Hinweis dafür, dass Dioxin die Zeugung von Jungen verhindert, wie eine
Schlagzeile in der Presse behauptete?
Prüfen Sie dies durch Berechnung des 95%-Konfidenzintervalls!
Aufgabe 3
An 16-jährigen Schülern von Gymnasien und Mittelschulen wurde in einer Studie unter anderem auch der Body-Mass-Index (BMI) [Körpergewicht in kg / (Körpergröße in m)2] bestimmt.
In folgendem Box-Plot ist der BMI für 40 Gymnasiasten dargestellt. Für 40 weitere Schüler
aus einer Mittelschule wurden für BMI folgende Werte ermittelt: Minimum=17; Maximum=33;
1.Quartil=20; Median=21,5; 3.Quartil=25.
a)
Skizzieren Sie das Box-Plot des BMI für Mittelschüler neben dem Box-Plot für Gymnasiasten.
b)
c)
d)
Body-Mass-Indizes ab 25 gelten als auffällig. Geben Sie die relative Häufigkeit (Prävalenz) von Schülern mit auffälligem Body-Mass-Index in dieser Mittelschule an!
Mit einem statistischen Test wurde der beobachtete Unterschied auf einem Signifikanzniveau von 5% geprüft. Der ermittelte p-Wert betrug p=0,0004. Welche Testentscheidung treffen Sie und welche Schlussfolgerung ziehen Sie?
Welcher statistische Test ist in dieser Situation der angemessene? Begründen Sie!
SS 2007
1
INSTITUT FÜR MEDIZINISCHE INFORMATIK, STATISTIK UND EPIDEMIOLOGIE
Aufgabe 4
Bereits im Kindesalter steigt der Anteil von Kindern mit Adipositas. In einer Studie wurde der
Effekt einer Therapie bestehend aus Bewegungsprogrammen und Ernährungsschulung untersucht. Dazu erhielten 95 übergewichtige Kinder im Alter von 8-12 Jahre diese Therapie
Interventionsgruppe). Eine Gruppe von 90 gleichaltrigen übergewichtigen Schülern ohne
diese Therapie diente als Kontrollgruppe. In der Interventionsgruppe konnten 65% der Kinder
innerhalb eines Jahres ihren Body-Mass-Index reduzieren. In der Kontrollgruppe gelang dies
im genannten Zeitraum nur 50% der Schüler. Die Kinder wurden den beiden Gruppen nach
dem Zufallsprinzip zugeordnet. Dabei wurde das Geschlecht berücksichtigt, so dass Jungen
und Mädchen in den beiden Gruppen etwa gleich verteilt sind.
a)
Charakterisieren Sie das Studiendesign durch 3 Attribute!
b)
Stellen Sie aus diesen Angaben die Vierfeldertafel auf. Runden Sie die absoluten
Häufigkeiten auf ganze Zahlen)!
c)
Testen Sie auf einem Signifikanzniveau von α=5%, ob sich Interventions- und Kontrollgruppe bzgl. der Reduktion im Body-Mass-Index unterscheiden! Interpretieren Sie
das Testergebnis! Hinweis: Testvoraussetzungen sind erfüllt.
Aufgabe 5
Um zu beurteilen, ob ein spezielles Aufwärmtraining einen Einfluss auf die Bewegungsqualität beim Basketballwurf hat, wurde bei 18 Sportlern vor und nach dem Training die Bewegungsqualität anhand einer Punktebewertungsskala gemessen (hohe Werte bedeuten gute
Bewegungsqualität). Beurteilen Sie den Einfluss des Aufwärmtrainings durch einen geeigneten statistischen Test bei α=5%.
nr
vorher
nachher
1
1,00
2
2,00
8,00
7,00
3
3,00
10,00
10,00
4
4,00
12,00
9,00
5
5,00
9,00
8,00
6
6,00
13,00
13,00
7
7,00
10,00
12,00
8
8,00
13,00
11,00
9
9,00
14,00
7,00
10
10,00
9,00
7,00
11
11,00
12,00
11,00
12
12,00
12,00
10,00
13
13,00
11,00
11,00
14
14,00
9,00
10,00
15
15,00
8,00
7,00
16
16,00
10,00
11,00
17
17,00
11,00
10,00
18
18,00
12,00
10,00
Insgesamt
N
Mittelwert
Standardabweichung
SS 2007
13,00
differenz
12,00
18
18
18
9,5000
10,8889
9,7778
5,33854
1,84355
1,89599
1,93691
2