Algebra, Geometrie

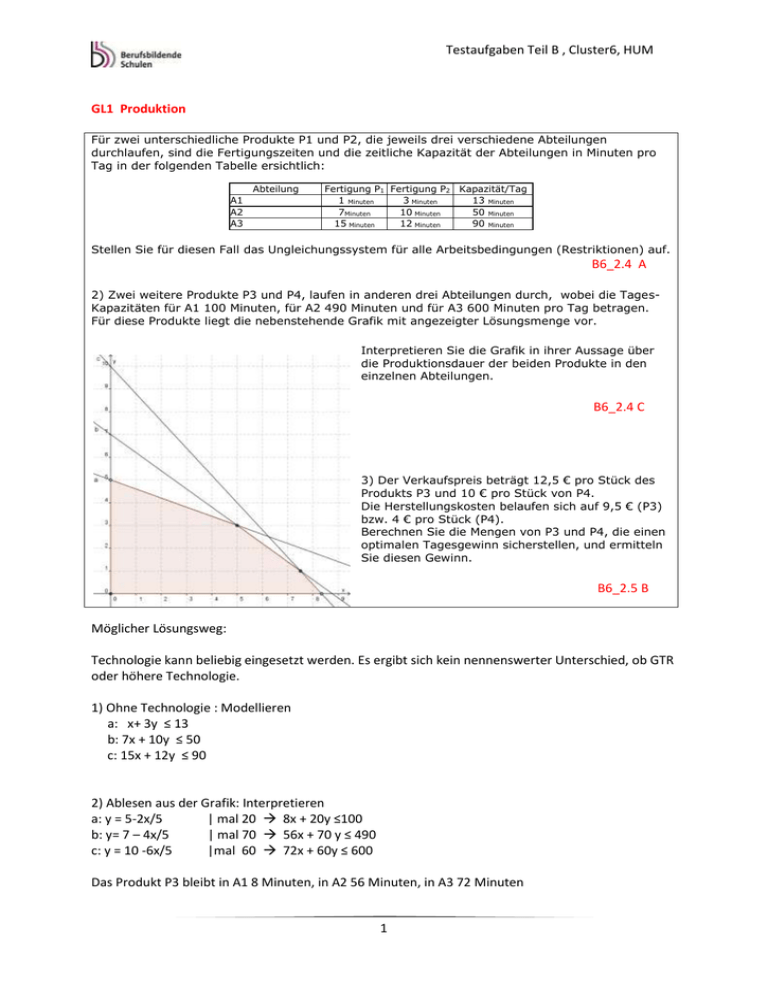
Testaufgaben Teil B , Cluster6, HUM
GL1 Produktion
Für zwei unterschiedliche Produkte P1 und P2, die jeweils drei verschiedene Abteilungen
durchlaufen, sind die Fertigungszeiten und die zeitliche Kapazität der Abteilungen in Minuten pro
Tag in der folgenden Tabelle ersichtlich:
Abteilung
A1
A2
A3
Fertigung P1 Fertigung P2 Kapazität/Tag
1 Minuten
3 Minuten
13 Minuten
7Minuten
10 Minuten
50 Minuten
15 Minuten
12 Minuten
90 Minuten
Stellen Sie für diesen Fall das Ungleichungssystem für alle Arbeitsbedingungen (Restriktionen) auf.
B6_2.4 A
2) Zwei weitere Produkte P3 und P4, laufen in anderen drei Abteilungen durch, wobei die TagesKapazitäten für A1 100 Minuten, für A2 490 Minuten und für A3 600 Minuten pro Tag betragen.
Für diese Produkte liegt die nebenstehende Grafik mit angezeigter Lösungsmenge vor.
Interpretieren Sie die Grafik in ihrer Aussage über
die Produktionsdauer der beiden Produkte in den
einzelnen Abteilungen.
B6_2.4 C
3) Der Verkaufspreis beträgt 12,5 € pro Stück des
Produkts P3 und 10 € pro Stück von P4.
Die Herstellungskosten belaufen sich auf 9,5 € (P3)
bzw. 4 € pro Stück (P4).
Berechnen Sie die Mengen von P3 und P4, die einen
optimalen Tagesgewinn sicherstellen, und ermitteln
Sie diesen Gewinn.
B6_2.5 B
Möglicher Lösungsweg:
Technologie kann beliebig eingesetzt werden. Es ergibt sich kein nennenswerter Unterschied, ob GTR
oder höhere Technologie.
1) Ohne Technologie : Modellieren
a: x+ 3y ≤ 13
b: 7x + 10y ≤ 50
c: 15x + 12y ≤ 90
2) Ablesen aus der Grafik: Interpretieren
a: y = 5-2x/5
| mal 20  8x + 20y ≤100
b: y= 7 – 4x/5
| mal 70  56x + 70 y ≤ 490
c: y = 10 -6x/5
|mal 60  72x + 60y ≤ 600
Das Produkt P3 bleibt in A1 8 Minuten, in A2 56 Minuten, in A3 72 Minuten
1
Testaufgaben Teil B , Cluster6, HUM
Das Produkt P4 bleibt in A1 20 Minuten, in A2 70 Minuten, in A3 60 Minuten.
3) Aufstellen der Zielfunktion;
Ermitteln des Gewinns (Kopfrechnen)
P3
P4
Verkauf
12,5
10
Z: 3x + 6y max!
Kosten
9,5
4
Gewinn
3
6
y = -0,5x
In der Grafik (Angabe) die Gerade einzeichnen und parallel verschieben
 Ablesen des Punktes (5/3).
Es sollen 5 Stück von P3 und 3 Stück von P4 hergestellt werden, das ergibt einen Tagesgewinn von
39€
Das kann mit Technologieeinsatz auch gemacht werden  GTR, Geogebra, EXCEL…
2