Aufgaben3

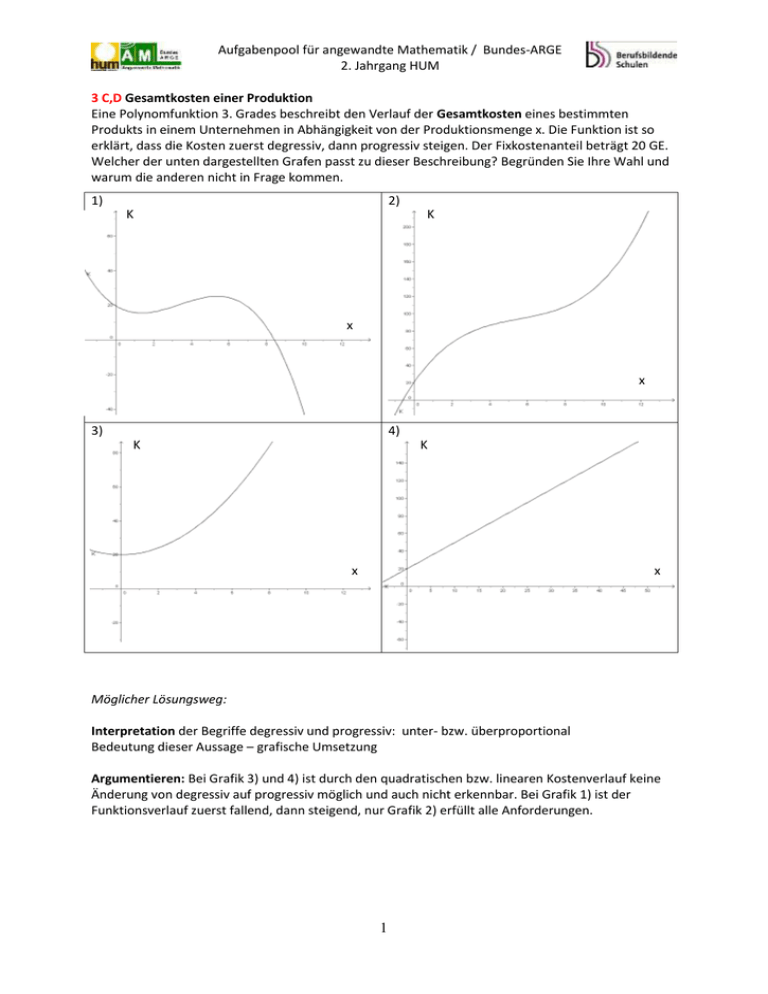
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 C,D Gesamtkosten einer Produktion
Eine Polynomfunktion 3. Grades beschreibt den Verlauf der Gesamtkosten eines bestimmten
Produkts in einem Unternehmen in Abhängigkeit von der Produktionsmenge x. Die Funktion ist so
erklärt, dass die Kosten zuerst degressiv, dann progressiv steigen. Der Fixkostenanteil beträgt 20 GE.
Welcher der unten dargestellten Grafen passt zu dieser Beschreibung? Begründen Sie Ihre Wahl und
warum die anderen nicht in Frage kommen.
1)
2)
K
K
x
x
3)
4)
K
K
x
x
Möglicher Lösungsweg:
Interpretation der Begriffe degressiv und progressiv: unter- bzw. überproportional
Bedeutung dieser Aussage – grafische Umsetzung
Argumentieren: Bei Grafik 3) und 4) ist durch den quadratischen bzw. linearen Kostenverlauf keine
Änderung von degressiv auf progressiv möglich und auch nicht erkennbar. Bei Grafik 1) ist der
Funktionsverlauf zuerst fallend, dann steigend, nur Grafik 2) erfüllt alle Anforderungen.
1
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3C, D Betriebsoptimum
Die unten dargestellte Grafik zeigt eine Stückkostenfunktion (= Funktion der durchschnittlichen
Kosten = K/x). Erklären Sie den Verlauf der Funktion und ermitteln Sie aus der Grafik die Menge x,
die die geringsten Stückkosten verursacht.
K/x in Geldeinheiten/Mengeneinheit
x in Mengeneinheiten
Möglicher Lösungsweg:
Argumentieren: Die Stückkostenfunktion ist eine gebrochen rationale Funktion (K(x)/x), daher an der
Stelle 0 nicht definiert. Die Stückkosten nehmen zunächst stark ab, erreichen dann einen minimalen
Wert und nehmen langsam wieder zu.
Interpretieren: Die geringsten Stückkosten liest man aus der Grafik bei ca. 15 ME ab.
2
Aufgabenpool für angewandte Mathematik / Bundes-ARGE
2. Jahrgang HUM
3 C,D Wirtschaftsfunktionen (Basis 2. JG)
Die unten dargestellte Grafik zeigt
1. eine Kostenfunktion K 3. Grades, die die gesamten Kosten beschreibt, die bei der Herstellung
eines Produkts anfallen.
2. eine lineare Erlösfunktion E, die die Einnahmen beschreibt, die man beim Verkauf des Produktes
hat, sowie
3. die Gewinnfunktion G, die man mit G = E - K erhält.
Ordnen Sie diese Begriffe den Funktionen in der Grafik zu und erklären Sie auch, was die
Besonderheit der eingezeichneten Punkte (BE, GG, KK, Gmax) ausmacht.
E,K,G
x
Möglicher Lösungsweg:
Lineare Erlösfunktion E ist die Gerade und geht durch den Ursprung: Wenn man nichts verkauft, dann
hat man auch keine Einnahmen.
Die Kostenfunktion schneidet die y-Achse. Dieser Schnittpunkt bezeichnet jene Kosten, die anfallen,
noch etwas hergestellt zu haben = Fixkosten. KK heißt Kostenkehre, ab diesem Punkt nehmen die
Kosten progressiv zu.
Gewinnfunktion muss dort die Nullstellen haben, wo Kosten und Erlös gleich groß sind, also die
Schnittpunkte der beiden Funktionen. BE... break even – Gewinnschwelle, weder Gewinn noch
Verlust,G = 0, es wird kostendeckend gearbeitet, am Beginn der Gewinnzone
GG... Gewinngrenze – kostendeckend, am Ende der Gewinnzone, ab dieser Menge steigen die Kosten
so stark an, dass die Erlöse die Kosten nicht mehr abdecken können, daher Übergang in Verlust!
Gmax...maximaler (größtmöglicher) Gewinn.
3