Mittelwert und Standardabweichung bei wiederholter Beobachtung

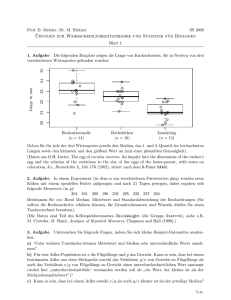
1
D:\68623242.doc
Mittelwert und Standardabweichung bei wiederholter Beobachtung mit
unterschiedlichen Genauigkeiten
Jörg Ihringer
Ein Messwert werde N mal erfasst, aber mit unterschiedlicher Genauigkeit. Jede Beobachtung
Nr. j liefere einen Messwert x j und eine Standardabweichung  j . Aus diesen Wertepaaren
kann der Mittelwert x der Messgröße und die Standardabweichung  x des Mittelwerts berechnet werden.
xj
Messwert bei Beobachtung Nr. j
j
Standardabweichung zur dieser Beobachtung
N
Anzahl der Beobachtungen
xj
N
x

j
N
1
j 1
j

 x2 
2
j 1
Mittelwert für x
2
1
N
1
j 1
j

2
Varianz, Quadrat der Standardabweichung,
von x
Tabelle 1 Mittelwert und Standardabweichung bei wiederholter Beobachtung mit unterschiedlichen Genauigkeiten
Den Mittelwert folgt entweder aus der Forderung nach der kleinsten Summe der gewichteten
Fehlerquadrate oder aus der Forderung nach größter Wahrscheinlichkeit für den gesamten
Satz der Messwerte. Diese Wahrscheinlichkeit wird mit der „Likelihood-Funktion“ formuliert.
Kennt man den analytischen Ausdruck für den Mittelwert, dann kann die Standardabweichung des Mittelwerts aus den partiellen Ableitungen des Mittelwerts nach den die Messwerte
repräsentierenden Variabeln und ihren Standardabweichungen bestimmt werden („Fehlerfortpflanzungs-Gesetz“).
Berechnung des Mittelwerts mit Hilfe der Likelihood-Funktion
Die „Likelihood-Funktion“ ist vor allem in der angelsächsischen Literatur gebräuchlich, auch
sie führt auf die Summe der Fehlerquadrate. Das Ergebnis jeder einzelnen Messung, z. B. der
Wert x j der Messung Nr. j , wird als Stichprobe aus einer Gaußverteilung mit Mittelwert x
und Standardabweichung  j aufgefasst. Nach jeder Messung überlegt man sich nun, mit
welcher Wahrscheinlichkeit ein Messwert zwischen x j und x j  dx zu erwarten war („aposteriori-Wahrscheinlichkeit“). Nach allen N Messungen formuliert man aus dem Produkt aller
Einzel-Wahrscheinlichkeiten die Wahrscheinlichkeit für den gesamten Satz der Ergebnisse
(unabhängige Beobachtungen vorausgesetzt). Die Variable in diesem Produkt, x , wird aus
2
D:\68623242.doc
der Forderung berechnet, dass das Produkt, d. h. die Wahrscheinlichkeit für den ganzen Satz
der Beobachtungen, maximal wird.
60
Häufigkeit
40
Beispiel: Histogramm von 500 Messungen
des Werts Nr. j zum Mittelwert x  0 und
 j =1.
20
0
-3
-2
-1
0
1
2
3
x
Messwert
j
dP
j
N
dP  L  dx  
j 1
N
L
j 1

1
 f ( x j , x )  dx 
2  j

1
e
2  j

1
e
2  j
e
Wahrscheinlichkeit, einen Messwert zwischen x j und x j  dx aus einer Gaußvertei-
x j  x 2
2 j 2
dx
Wahrscheinlichkeit, den ganzen Satz mit N
Messwerten zwischen x j und x j  dx
x j  x 2
2 j 2
dx
x j  x 2
2 j 2
1 N x j  x 
l 
 const.
2 j 1  j 2
2
N x x
N
N
xj
dl
1
j



x

0


2
2
2
d j 1  j
j 1  j
j 1  j
N
x
lung mit Mittelwert x und Standardabweichung  j zu erhalten.
( j  (1,2,..N ) bei Mittelwert x und den
Standardabweichungen  j zu erhalten
Definition der Likelihood Funktion. Zur
Erleichterung der Rechnung bildet man den
Logarithmus der Likelihood Funktion, das
ist – bis auf die Konstante- die Summe der
gewichteten Fehlerquadrate.
Bedingung für das Maximum, es folgt daraus der
xj

2
j 1
j
N
1
j 1
j

Mittelwert
2
Tabelle 2 Berechnung des Mittelwerts bei wiederholter Beobachtung mit unterschiedlichen
Genauigkeiten mit Hilfe der Likelihood-Funktion
3
D:\68623242.doc
Berechnung der Standardabweichung des Mittelwerts
Die Standardabweichung  x des Mittelwerts x folgt aus dem „Fehlerfortpflanzungs-Gesetz“
als Funktion der Standardabweichungen  j .
N
x
xj

2
j 1
j
N
1
j 1
j


Z(x)
N
2
N
xj
j 1
 j2
Z(x)  
Mittelwert, aufgeteilt in Zähler Z und Nenner N. Nur Z hängt vom Vektor x der
Messwerte ab.
Z(x)
1
 2
x j
j
N
1
j 1
 j2
N
x
2
 x
 

j 1  x j
N
2

2

 j

 xx
2
x
 x2 
2
1 N  Z( x) 
2
 2  
 j
N j 1  x j  x x
1 N 1
1
2

 j  
2 
4
N
N j 1  j
Fehlerfortpflanzungsgesetz, Z und N eingesetzt
1
N
1
j 1
j

2
Tabelle 3 Berechnung der Standardabweichung des Mittelwerts aus dem Fehlerfortpflanzungsgesetz
Literatur: z.B. S. Brandt, Datenanalyse, (1992), BI Wissenschaftsverlag Mannheim/Leipzig/Wien/Zürich
Zur Skripten Seite:
http://www.uni-tuebingen.de/uni/pki/skripten/skripten.html