Angabe des Messwerts und Fehlerabschätzung
Werbung

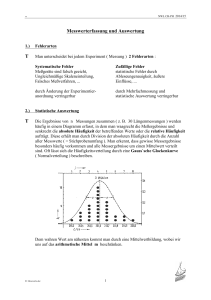
Manual zur Angabe des Messwerts und der Fehlerabschätzung 1) Messungen sind immer fehlerhaft Da einerseits Messgeräte nicht 100 % genau sind und andererseits der Beobachter nicht vollkommen ist, stimmt der Messwert mit dem wahren Wert nicht überein. Dazu kommt noch, dass äußere Einflüsse sich ebenfalls auf die Messungen auswirken. So gesehen sind Messungen immer fehlerbehaftet. Man unterscheidet zwei Arten von Messfehlern, die zum sogenannten „absoluten Messfehler x“ der Messgröße x führen: zufällige Fehler systematische Fehler Ursachen sind: unverlässliche Sinnesorgane ungeschicktes Messen ungenaues Ablesen ungenaue Messgeräte wenig geeignete Messverfahren nicht korrigierte Einflüsse des Messgeräts auf das Messobjekt statistisch wirkende äußere Einflüsse wie T-Schwankungen, Luftdruckschwankungen systematische Fehler sind unter gleichen Bedingungen immer gleich, daher können sie korrigiert werden. zufällige Fehler streuen um einen Mittelwert, wobei zu beachten ist, dass die Abweichungen x positiv und negativ sein können. 2) Messwerte Messwert: Ergebnis einer Einzelmessung xi Messreihe: Wiederholtes Messen einer Messgröße unter mehr oder weniger gleichen Voraussetzungen n Mittelwert: Arithmetisches Mittel der Messwerte einer Messreihe x x i 1 i n , wobei „n“ die Anzahl der Messungen in der Messreihe ausdrückt. ACHTUNG: Eindeutig als falsch erkennbare Messwerte bleiben unberücksichtigt. Erwartungswert: Je größer die Anzahl der Messungen einer Messreihe ist, desto mehr nähert sich der Mittelwert einem Grenzwert, dem Erwartungswert. 1 G.Lechner/deptphywest/15.05.16 D:\68614991.doc 3) Ablesen von Messwerten, signifikante Stellen Beim Ablesen von Messwerten ist darauf zu achten, dass auf eine sinnvolle Anzahl von Stellen angegeben wird. Bsp.: Es hat nicht nur wenig Sinn, sondern es ist falsch bei der Messung von Längen mit einem Lineal die Länge auf 0,001 mm anzugeben. Es ist für jede Messung zu entscheiden, wie viele signifikante Stellen man angibt. Dabei ist in jedem Fall zu berücksichtigen, dass der Messwert ( oder auch das Ergebnis ) in einem Intervall liegt. 20 cm ist nicht identisch mit 20,0 cm 19,5 cm 20 cm 20,4 cm 19,95 cm 20,0 cm 20,04 cm 4) Rechengenauigkeit Setzt sich das Ergebnis aus mehreren Faktoren zusammen, so muss man achten, dass die Ergebnisse nie genauer sein können als die Einzelergebnisse. Vor allem bei der Benützung von Taschenrechnern ist die Gefahr gegeben, dass es durch Angabe zu vieler Stellen zu einer Scheingenauigkeit kommt. Grundregel: Die signifikanten Stellen des am ungenauest bekannten Wertes bestimmen die Genauigkeit des Resultats. Beispiel: m = 1,555 kg: V = 2,2 m³ 1,555 kg kg kg = 0,7068 3 0,7 3 3 m 2,2 m m 5) Absoluter Fehler Der absolute Fehler ist die Differenz zwischen Messwert und Mittelwert (wahrer Wert) x x xi Da absolute Fehler positiv wie negativ sein können, wird mit Zunahme der Messzahl die xi 0 gehen. Dies kann als Kontrolle für die Genauigkeit der Messungen i herangezogen werden. a) Absoluter Fehler und Einzelmessung Bei Einzelmessungen wird der Fehler abgeschätzt. b) Absolute Fehler und die Standardabweichung Aufgrund der zufälligen Fehler streuen die Messwerte um den Mittelwert. Ein Maß für die Zuverlässigkeit der einzelnen Messwerte in einer Messreihe ist die Standardabweichung. Sie bestimmt die durchschnittliche Abweichung vom 2 G.Lechner/deptphywest/15.05.16 D:\68614991.doc mittelwert und wird daher auch als „mittlerer quadratischer Fehler der Einzelmessung“ bezeichnet: x i n n 2 i x2 x i 1 i x 2 n 1 ACHTUNG: Die Herleitung beruht auf statistischen Methoden. Vielleicht ist auch bekannt. dass 2 als die Varianz bezeichnet wird Der Nenner ( n - 1) entspricht der Anzahl der Freiheitsgrade bei der Berechnung. Der Grund für ( n - 1 ) ist, dass für die Werte xi eine kleine Einschränkung gegeben ist. Um die Standardabweichung berechnen zu können, müssen wir zunächst den Mittelwert kennen. Wenn man nun z.B. zehn Werte hat, so können neun frei gewählt werden, der zehnte Wert ist aber an den Mittelwert gebunden. So verliert man auf diese Weise einen Freiheitsgrad. Je höher die Anzahl der Messungen ist, desto weniger Einfluss hat der Verlust des Freiheitsgrades. Daher ist es auch leicht einsichtig, dass für solche n Messreihen die Standardabweichung übergeht in x i 1 i x 2 n 68,3 % der Messwerte liegen im Bereich x , 95,4 % im Bereich x 2 und 99,73 % im Bereich x 3 c) Vertrauensbereich des Mittelwerts Der Mittelwert ist meist nicht identisch mit dem richtigen gesuchten Wert, daher ist es wesentlich zu wissen, mit welcher statistischen Sicherheit der Mittelwert betrachtet werden kann. Es wird dieser Wert deshalb auch als der mittlere Fehler des Mittelwerts bezeichnet. Es werden daher zwei Grenzen angegeben zwischen denen der wahre Wert mit einer bestimmten Sicherheit liegt. Die Breite dieser Zone oberhalb und unterhalb des Mittelwerts errechnet sich folgend: t , wobei t en Wert ist, der von der statistischen Sicherheit abhängt. n n t x i 1 i x n n 1 2 ; für 10 Messwerte liefert t = 1,06 eine statistische Sicherheit von 68,3 % und t = 2,3 eine statistische Sicherheit von 95 % 3 G.Lechner/deptphywest/15.05.16 D:\68614991.doc 5) Relativer Fehler und Angabe des Messergebnisses Der absolute Fehler als solcher gibt keinen Aufschluss über die Stärke einer Messung. Aus diesem Grund setzt man den absoluten Fehler in eine Beziehung zum Mittelwert. relativer Fehler: x 100 % x Welchen absoluten Fehler man verwendet hängt von der Interpretation des Messergebnisse ab: x ; x ACHTUNG: In den angeführten Fällen ist die Messunsicherheit ohne systematischen Fehler angeführt. Im Falle der Berücksichtigung systematischer Fehler setzt sich die Messunsicherheit aus dem absoluten Fehler und dem systematischen Fehler zusammen ! 6) Fehlerfortpflanzung Ergibt sich das Ergebnis aus einer Funktion, die sich aus mehreren Messwerten zusammensetzt, sind folgende Regeln zu beachten ( ohne Beweis): Summe und Differenz: z x y z x y Produkt und Quotient: z x y z Potenz: z x y z x y x y z xn z x n z x Die Fehlerfortpflanzung für Funktionen mit einer unabhängigen veränderlichen bzw. mit mehreren unabhängigen veränderlichen ist über die Differentialrechnung bzw. über das totale Differential durchzuführen. 4 G.Lechner/deptphywest/15.05.16 D:\68614991.doc