Blatt 11 - userpages

Universität Koblenz-Landau
FB 4 Informatik
1
Prof. Dr. Viorica Sofronie-Stokkermans∗
2
Dipl.-Inform. Markus Bender∗
11.07.2014
Übung zur Vorlesung Logik für Informatiker
Aufgabenblatt 11
Abgabe bis 18.07.2014, 15:00 s.t.
Aufgabe 11.1
Sei Σ = (Ω, Π) eine Signatur, wobei
• Ω = ∅, und
• Π = {p/1, q/1, r/2}.
Ferner sei X eine Menge von Variablen und x, y, z ∈ X.
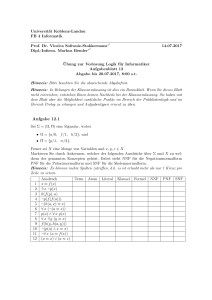
Markieren Sie durch Ankreuzen, welche der folgenden Formeln über Σ und X in NNF,
bereinigt, in Pränexnormalform, in Skolemnormalform sind.
Hinweis: Es können mehre Spalten zutreffen, d.h. es ist erlaubt mehr als nur 1 Kreuz pro
Zeile zu setzen.
NNF bereinigt Pränexnormalform Skolemnormalform
p(x) → r(x, y)
¬(p(x) ∨ r(x, y))
(∀x q(x)) ∧ (∃x r(x, y))
∀x∀y(p(x) ∨ r(x, y))
∀x∃y(p(x) ∨ r(x, y))
(∀x r(x, y)) ∧ (∀z p(x) ∨ q(z))
(∀x r(x, y)) ∨ ¬(∃z p(x) ∨ q(z))
∀x∃z∀y (r(x, y) ∨ ¬(p(x) ∨ q(z)))
Aufgabe 11.2
Sei Σ = (Ω, Π) eine Signatur, wobei
• Ω = ∅, und
• Π = {r/2}.
Ferner sei X eine Menge von Variablen und x, y, z ∈ X.
Gegeben sei die folgende Formel über Σ und X:
F = ∃x∀y ¬r(y, x) ↔ ¬∃z(r(y, z) ∨ r(z, y))
Transformieren Sie F nach Pränexnormalform und geben Sie dabei alle Zwischenschritte
explizit an (Negationsnormalform, bereinigte Form, Pränexnormalform).
Aufgabe 11.3
Sei Σ = (Ω, Π) eine Signatur, wobei
• Ω = {f /1}, und
• Π = {q/2, r/3}.
Ferner sei X eine Menge von Variablen und v, w, x, y, z, z1 ∈ X.
Gegeben sei die folgende Formel über Σ und X:
F = ∃v∀w∃x∀y∃z q(f (y), z) ∨ r(w, y, w) ∨ r(w, x, z1 ) ∧ ¬r(z1 , v, f (x))
Geben Sie zur Formel F jeweils die folgenden Formen an:
a) die Skolemnormalform
b) die Skolemnormalform mit Matrix in konjunktiver Normalform
c) die Klauselnormalform (in Mengennotation)
Aufgabe 11.4
Sei Ω = {f /1, g/1, h/2} eine Menge von Funktionssymbolen, X eine Menge von Variablen
und v, w, x, y, z ∈ X.
Gegeben sind die folgenden 3 Unifikationsprobleme über Ω und X:
?
?
?
I) {g(v) = g(w), h(x, f (x)) = v, w = h(f (y), x)}
?
?
?
II) {g(v) = g(w), h(x, x) = v, w = g(y)}
?
?
?
III) {g(v) = g(w), h(x, f (y)) = v, w = h(f (y), z)}
a) Wenden Sie den Martelli-Montanari Algorithmus auf die gegebenen Probleme an. Notieren Sie dabei sämtliche Zwischenschritte und dabei auch den Namen der im Schritt
angewendeten Regel. Jeder Schritt soll der Anwendung genau einer Regel.
Hinweis: Achten Sie darauf, den Algorithmus so lange anzuwenden, bis keine Regeln
mehr anwendbar sind.
b) Verwenden Sie die Ergebnisse aus dem vorherigen Aufgabenteil um eine begründete
Aussage über das (Nicht-)Vorhandensein eines Unifikators zu machen. Gibt es einen
Unifikator für ein Probleme, so geben Sie ihn explizit an.
Aufgabe 11.5
Erstellen Sie die Wissensbasis solution11.pl, und definieren Sie in ihr das Prädikat
eamv(EL, AL) (entferne aufeinaderfolgende mehrfache Vorkommen), das genau dann wahr
ist, wenn die Liste AL der Liste EL entspricht, wobei alle direkt aufeinanderfolgenden mehrfachen Vorkommen eines Atoms auf ein einzelnes Vorkommen reduziert wurde.
EL (somit auch AL) sind flache Listen, d.h. es kommen keine verschachtelten Listen vor.
Zur Verdeutlichung einige Beispielaufrufe:
Eingabe
eamv([a,
eamv([a,
eamv([a,
eamv([a,
eamv([a,
eamv([a,
b,
a,
a,
a,
a,
a,
c,
a,
b,
b,
b,
b,
d], AL).
a, b, c, d], AL).
a, b], AL).
b, a, a, b, b], AL).
a, b], [a, a, b, a, b]).
a, b], [a, b, a, b]).
Ausgabe
AL=[a, b,
AL=[a, b,
AL=[a, b,
AL=[a, b,
false
true
c,
c,
a,
a,
d]
d]
b]
b]
Prolog soll für jeden Aufruf exakt eine Antwort zurück geben, es gibt also keine Möglichkeit
nach weiteren Antworten zu fragen.
Bis auf die folgenden Ausnahmen dürfen Sie keine built-in Prädikate und keine Arithmetik
verwenden:
• den Cut-Operator ‘!’,
• das Prädikat ‘fail’, das immer falsch ist,
Achten Sie darauf, dass es beim Laden Ihrer Wissensbasis zu keinen Fehlern oder Warnungen kommt.
∗1
∗2
B 225
B 224
[email protected]
[email protected]
www.uni-koblenz.de/~sofronie
www.uni-koblenz.de/~mbender
Bitte beachten Sie die Modalitäten zur Abgabe, die Sie unter http://userp.uni-koblenz.de/~mbender/
ss14logic.html einsehen können.