Aufgabenbeispiel zu "offene Fragestellungen

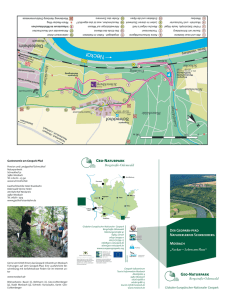
Auguste Pattberg Gymnasium
Mosbach Neckarelz
- Fachbereich Mathematik -
Betr.:
Mosbach, Februar 1999
Beispiel einer Aufgabe für offene Fragestellungen, Anwendungsbezug
und fächerübergreifende Thematik
Ergebnisse der Fachkonferenz vom 28.1.1999
Aufgabenbeispiel zu "offene Fragestellungen, Anwendungsorientierung,
fächerübergreifende Probleme"
Text:
Um die Bekämpfung von Schadinsekten zu optimieren, beobachtet man in gleichen
Zeitintervallen (z.B.2 Wochen) die Dichte des Befalls, indem man die Anzahl der Insekten
pro dm2 großflächig auszählt und dann den Mittelwert bildet.
Diese Werte trägt man in ein Koordinatensystem ein.
Mögliche Fragestellungen
Schadinsekten pro dm2

denkbar



Welche Fragestellungen sind für ein
solches Problem relevant ?
Welche analytischen Ansätze können
zu ihrer Beantwortung beitragen ?
Beschreiben Sie den zeitlichen Verlauf
des Befalls durch ein möglichst einfache,
aber für die Meßwerte passende ganzrationale Funktion.(alternativ: Funktionsgrad vorgeben)
Welche Kriterien haben Ihre Wahl beeinflußt ?
Bestimmen Sie die Gleichung einer solchen
Funktion mit Hilfe der Meßwerte.
Welche weiteren Informationen lassen sich
mit Hilfe der Modellfunktion gewinnen ?
Wo liegen die Grenzen, wenn nicht sogar
Fehler des Modells ?
5
4
3
2
1
0
1
2
3
4
5
Zeitintervalle
6
Lösungen:

Von Interesse sind: Maximaler Befall, Prognose des Befalls, Periode stärkster Vermehrung,
durchschnittlicher Befall, Ende des Befalls.
Mittels einer geeigneten Funktion, der Berechnung von Nullstellen,
Extremstellen, Wendestellen, Steigungen und Flächenberechnungen
lassen sich die oben genannten Fragen beantworten.

Erstellung der Funktionsgleichung mit Hilfe geeigneter Wertepaare.
5
9
5
y   x 3  x 2  x; x  ( theoretisc h)
24
8
12
Da lineare Funktionen ausscheiden, quadratische Funktionen aber
achsensymmetrische Schaubilder liefern, bleibt eigentlich nur eine
Funktion dritten Grades übrig, zumal es sich um eine möglichst
einfache ganzrationale Funktion handeln soll.

Durchführung einer vollständigen Kurvendiskussion.
N1(0/0); N2(0,4/0); N3(5/0) H(3,4/3,4); T(0,2/-0.04); W(1,8/1,7)
Vervollständigen des Schaubildes (oder neu zeichnen).
0,2
5
0
0,2
Berechnung des  f ( x )dx und  f ( x )dx sowie des Quotienten

Fläche
. (Ergebnis: Durchschnitt = 1,83Ins/dm2)
Zeit int ervall
Kritische Auseinandersetzung mit dem Modell und seinen Ergebnissen.
Prognose kaum möglich (erneuter Anstieg denkbar), negative
Funktionswerte im Zeitintervall [0,1], unsichere Aussagen auf Grund der
Diskrepanz zwischen diskret verteilten Meßdaten und stetiger, ja sogar
differenzierbarer Modellfunktion.
Vorbehalte und Kritik
Die Kolleginnen und Kollegen des Fachbereichs Mathematik haben im Zuge einer Fachkonferenz
eine Reihe von kritischen Aspekten zu solchen Fragestellungen formuliert. Die Fachkonferenz legt
ebenfalls Wert auf die Feststellung, daß die Probleme mit den diesjährigen Abituraufgaben nicht
im Anwendungsbezug zu suchen waren, sondern in einem durch den geforderten Umfang
begründeten zeitlichen und handwerklichen Defizit.
Außerdem erinnern sich alle noch sehr gut an eine frühere Fortbildungsveranstaltung zum
Thema "Aufgabenstellung", in der damals (vor ca. 10 Jahren) verlangt wurde, daß
Fragestellungen eindeutig und unmißverständlich Sinn und Frageinhalt der Aufgabe
dokumentieren sollen (Hr. Fillbrunn!).
Detailliert ist mit folgenden Problemen beim obigen Beispiel zu rechnen.:
-
Breiter und variabler Erwartungshorizont 

-
Notwendigkeit intensiver Einübung



-
Leitcharakter der Einstiegsfrage



-
Grenzen von Anwendungsbezug und
Offenheit der Fragestellung



Verunsicherung von Schüler und Korrektor
Überforderung, wenn der Schüler allen
Eventualitäten gerecht werden will.
Noch mehr Mängel im handwerklichen
Bereich.
Verlust der Flexibilität in der Anwendung von
mathematischen Lösungsmethoden.
Diskrepanz zwischen Strategie und
rechnerischen Umsetzung.
Bewertung unterschiedlichster
Interpretationen.
"Trifft der Schüler nicht das erwünschte
Fahrwasser, so gerät er rechnerisch in
Teufels Küche"
Abitur: ??Thema verfehlt ??
Überforderung (bes. Grundkurs).
Spielerei mit den Steckenpferden von
Lehrern und Aufgabenstellern.
Verlust der Vergleichbarkeit in Anforderung
und Ergebnis.
Mit kollegialem Gruß
Die Kolleginnen und Kollegen des Fachbereichs Mathematik
des Auguste Pattberg Gymnasiums, Mosbach Neckarelz
i.A. Rudi Kolb