AusarbeitungDiffererentialrechnungDanielaHinz

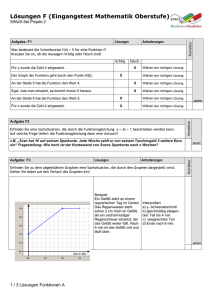
Ausarbeitung zur Einführung in die Differentialrechnung
Mathematikdidaktik B, Didaktik der Sek II
21. Dezember 2009
Daniela Hinz
Studienfächer Mathematik und Biologie
Fachsemester: 5./ 9.
In der vorliegenden Ausarbeitung soll dargestellt werden, welche Möglichkeiten es gibt, die
Differentialrechnung im Unterricht einzuführen. Dabei wird auf verschiedene
Grundvorstellungen vom Ableitungsbegriff eingegangen. Es sind unter anderem folgende
Grundvorstellungen vom Ableitungsbegriff möglich (vergleiche auch Blum/ Kirsch in
mathematik lehren, Heft 78):
• Steigung der Tangente/ des Funktionsgraphen an einer Stelle
• Lineare Approximation
• Grenzwert
• Lokale (momentane) Änderungsrate
• Momentangeschwindigkeit
• Umfang eines Kreises
• Grenzsteuersatz (als Ableitung der Funktion, welche die Einkommenssteuer abbildet)
• Kraft (als Ableitung der Arbeit nach dem Weg)
• Oberfläche der Kugel (als Ableitung des Kugelvolumens nach dem Radius)
• Querschnitt des Körpers in einer bestimmten Höhe (als Ableitung des Volumens eines
Körpers dieser Höhe)
• Ordinate des Kurvenpunktes/ Höhe an dem Punkt (als Ableitung des Flächeninhalts
unter der Kurve bis zu diesem Punkt)
• Funktionswert (als Ableitung des Integrals)
Die zentralsten Begriffe sind hierbei (vergleiche die Darstellung Schneiders in mathematik
lehren, Heft 102) zum einen der Begriff der lokalen Änderungsrate und zum anderen der
Begriff der linearen Approximation, d.h. der Tangentensteigung bzw. des Grenzwertes der
Sekantensteigungen.
Im Folgenden werden drei Möglichkeiten der Einführung in die Differentialrechnung genauer
ausgeführt: ein Einstieg mit Hilfe von Computer-Algebra-Systemen (CAS), der auf der
klassischen Vorstellung der Ableitung als Tangentensteigung basiert, ein Einstieg, bei dem
anhand von mathematischen Sätzen und Definitionen das mathematische Argumentieren
geübt werden kann und ein Einstieg über das Konzept des lokale Änderungsverhaltens,
welches auf einer Studie aus dem Bereich der didaktischen Rekonstruktion basiert. Dabei
wird jeweils diskutiert, welche Voraussetzungen dafür jeweils von Seiten der Schüler
notwendig sind und welche langfristigen und kurzfristigen Unterrichtsziele dabei angestrebt
werden.
Unterrichtsentwurf 1: Einstieg mit Hilfe von CAS/ Computer
Als erstes soll hier dargestellt werden, wie man kann CAS nutzen kann, um die
Differentialrechnung einzuführen. Geogebra bietet hierzu z.B. interaktive Arbeitsblätter im
Internet
an:
http://www.geogebra.org/de/examples/funktion_steigung/funktion_steigung1.html
http://www.geogebra.org/de/examples/funktion_steigung/funktion_steigung2.html
http://www.geogebra.org/de/examples/funktion_steigung/funktion_steigung3.html
Die hierbei angesprochene Grundvorstellung vom Ableitungsbegriff ist die Steigung der
Tangente am Graphen. Die Schüler können mit den oben angegebenen Arbeitsblättern selbst
Entdecken, dass der y-Wert des Ableitungsgraphen an einer Stelle x die Tangentensteigung
der Ursprungskurve an der Stelle x angibt. Allerdings benötigen die Schüler hierzu bei den
dargestellten Arbeitsblättern die Fähigkeit, formal eine (Polynom-) Funktion abzuleiten.
Notwendige Vorkenntnisse der Schüler:
- Grundlagen des Umgangs mit dem Computer
- Schüler müssen bei den dargestellten Arbeitsblättern bereits formal ableiten können
- Polynomfunktionen und Geradengleichungen müssen bekannt sein (Ablesen einer
Geradengleichung aus dem Graphen, Erkennen eines Graphen von Polynomfunktionen 2.
Und 3. Grades)
- die Schule muss entsprechende Ausstattung/ Räumlichkeiten haben
Mögliche Vor- und Nachteile dieses Unterrichtseinstiegs:
Vorteile:
- hoher Grad der Anschaulichkeit
- Zusammenhang zwischen Tangentensteigung und Ableitung ist klar sichtbar
- die Schüler können den Zusammenhang zwischen Ableitung und Tangentensteigung
selbst entdecken
- ein Arbeiten in unterschiedlichem Tempo ist möglich (innere Differenzierung), da jeder
Schüler alleine arbeiten kann (bei entsprechender Ausstattung der Schule)
Nachteile:
- Schüler müssen nicht selbst überlegen, wie die Ableitung aussehen könnte, wenn sie der
Tangentensteigung entspricht - der Computer zeichnet es selbständig
- bei den Arbeitsblättern in dieser Form müssen die Schüler bereits formal ableiten können;
meist ist es jedoch günstiger, das formale Ableiten an den Schluss einer
Unterrichtssequenz zu setzten, da dann die Grundkonzepte bereits verstanden worden sind
bevor das „Schema-Rechnen“ beginnt
- das Programm kann als Spielzeug missverstanden werden, so dass der mathematische
Hintergrund nicht erfasst wird
Kurzfristige und längerfristige Ziele, die durch diesen Unterrichtseinstieg angesteuert
werden sollen:
- Erkennen, dass die Steigung der Tangente an eine Funktion sowohl negativ als auch
positiv sein kann
- Beobachten, dass am „tiefsten" und „höchsten Punkt" des Graphen die Steigung gleich
Null ist
- Erkennen, dass die Steigung der Tangenten einer Parabel, als Funktion abgetragen, eine
Gerade ergibt
- Erkennen, dass die Steigung der Tangenten eines Polynoms dritten Grades, als Funktion
abgetragen, eine Parabel ergibt
- Erkennen und Verstehen des Zusammenhangs zwischen Tangentensteigung und
Ableitung einer Funktion
Bemerkung: Man könnte das Arbeitsblatt jedoch auch zur Wiederholung des
Zusammenhangs zwischen Ableitung und Tangentensteigung nutzen (z.B. im Anschluss an
Unterrichtsentwurf 3) oder aber ein anderes CAS Programm nutzen, bei dem der Übergang
von Sekanten zur Tangente für die Schüler beobachtbar ist und so der Differenzenquotient
und die Ableitung als deren Grenzwert entwickelt werden kann.
Unterrichtsentwurf 2:
Differentialrechnung
Üben
des
Argumentierens
mit
Hilfe
der
Heinrich Bürger und Günther Malle stellen in der Zeitschrift „mathematik lehren“ (Heft 103,
S.60) einen völligen anderen Zugang zur Differentialrechnung vor. Es geht dabei darum, dass
die Schüler am Beispiel der Differentialrechnung das mathematische Argumentieren lernen
bzw. üben. Da es im Bereich der Differentialrechnung eine überschaubare und wohl definierte
Argumentationsbasis (damit wird die Gesamtheit der beim Argumentieren verwendeten
Definitionen und Sätze bezeichnet) gibt, bietet sich dieser Zugang nach Bürger und Malle an.
Dabei werden zunächst den Schülern bereits bekannte Vorstellungen wie das Steigen und
Fallen einer Funktion oder intuitive Begriffe wie Maximum und Minimum aufgegriffen und
formal definiert sowie mit Graphen veranschaulicht. Die von Bürger und Malle
vorgeschlagene Argumentationsbasis, welche mit den Schülern gemeinsam erarbeitet werden
soll, sieht dann folgendermaßen aus:
Nachdem Schüler zunächst lernen, Graphen mit Hilfe des Monotonieverhaltens zu skizzieren,
sollen sie in einer zweiten Unterrichtsphase ihr Vorgehen auch mit Hilfe der
Argumentationsbasis begründen. Dabei werden sie nach Bürger und Malle wiederkehrende
Argumentationsketten aufdecken und dabei selbst Sätze entwickeln und diese mit Hilfe der
Argumentationsbasis auch beweisen. Die Schüler sollen, indem sie exemplarisch die
mathematische Art des Begründens praktizieren, ein unverfälschtes Bild der Mathematik
bekommen und präzises Begründen generell - auch bezogen auf andere Lebensbereiche –
lernen.
Notwendige Vorkenntnisse der Schüler:
- Grundlegende Kenntnisse über Funktionsgraphen (aus der Mittelstufe)
- eventuell Kenntnisse über das Verhalten von Funktionen (Begriffe wie steigend, fallend,
Maximum, Minimum)
- Begriff des Intervalls muss klar sein
- Schüler müssen bestimmte mathematische Notationen kennen (z.B. logischer Folgepfeil)
- Grundlagen der Mengenlehre (Teilmenge, Element)
- Schüler benötigen hohes Abstraktionsvermögen
Mögliche Vor- und Nachteile dieses Unterrichtseinstiegs:
Vorteile:
- Schüler üben abstraktes Denken und erhalten Einblick in strenge mathematische
Argumentationsweise
- Schülern lernen, dass man in der Mathematik sehr exakt und präzise arbeiten und jeden
Schritt begründen/ beweisen können muss
- Nähe zur Hochschulmathematik, so dass der Übergang von Schule zu Uni erleichtert wird
- für den Lehrer oft leichter, da dieser Zugang ihm aus der Uni bestens bekannt ist
Nachteile:
- wenig anschaulich
- sehr abstrakt
- für viele Schüler sicherlich abschreckend
- wenig praxisnah
- erzeugt eventuell ein falsches Bild von Mathematik als langweilige feinschrittige Theorie,
die benutzt werden muss, um zu zeigen, was man sowieso schon weiß
- die Argumentationsbasis muss zu einem großen Anteil vom Lehrer vorgegeben werden,
da die Schüler von selbst nicht auf solche abstrakte Formulierungen kommen werden
- es ist sehr fraglich, ob die Schüler in der Lage sind, das präzise Argumentieren auf andere
Fächer/ Lebensbereiche zu übertragen, wenn dieses lediglich an einem beschränkten Feld
der Mathematik geübt wird
Kurzfristige und längerfristige Ziele, die durch diesen Unterrichtseinstieg angesteuert
werden sollen:
- selbständiges Skizzieren von Funktionsgraphen anhand des Monotonieverhaltens
- Schüler lernen exakte Definition von Monotonie, Maximum, Minimum kennen
- eventuell erster Kontakt bzw. Üben der mathematisch-logischen Denkweise und Exaktheit
- Erkennen, dass aus bestimmten Sätzen in der Mathematik weitere Sätze abgeleitet werden
können
- selbständiges Ableiten und Beweisen von mathematischen Sätzen
- Nutzen von Sätzen in der Mathematik zum Argumentieren und Beweisen
Bemerkung: Bei dem dargestellten Entwurf handelt es sich nicht im engsten Sinne um einen
Einstieg sondern vielmehr um die Darstellung einer ganzen Unterrichtssequenz, die durch
einen besonderen Zugang (über die Argumentationsbasis) ausgezeichnet ist.
Unterrichtsentwurf 3: Einstieg über die Ableitung als momentanes/ lokales
Änderungsverhalten
Ein bedeutender Vorteil der Einführung der Ableitung als Änderungsverhalten ist der starke
Praxisbezug bzw. genauer die Relevanz beim Beschreiben, Modellieren und Lösen
praxisnaher Probleme.
Darüber hinaus greift ein solcher Einstieg optimal auf das Vorwissen der Schüler zurück, wie
Steffen Hahn in einer im Rahmen seiner Promotionsarbeit durchgeführten Studie zeigt
(vergleich Hahn/Prediger in JMD 29). Die Studie basiert auf der konstruktivistischen
Lerntheorie, welche auch durch neurophysiologische Untersuchungen gestützt wird. Die
Theorie besagt, dass Lernen die Eingliederung eines neuen Lerngegenstandes in bereits
vorhandene Strukturen beim jeweiligen Lerner darstellt. Nach dieser Theorie spielt
dementsprechend das Vorwissen des Lerners eine bedeutende Rolle (da dies die Möglichkeit
der Integration neuer Inhalte bestimmt). Dabei kommen im Mathematikunterricht als
Vorwissen sowohl alltagsweltliche Vorstellungen als auch vorunterrichtliche Vorstellungen
aus vergangenem (Mathe-) Unterricht zum Tragen.
Hahn untersuchte das Vorwissen von Schülern im Bezug auf die Differentialrechnung und
kam dabei zu dem Schluss, dass Schüler bereits vor Einführung der Differentialrechnung
weitreichende Vorstellungen vom Änderungsverhalten von Kurven haben (bei Wahl
geeigneter praxisnaher Beispiele). Schüler erkennen z. B. Wendepunkte und Extrema als
bedeutsame Stellen – selbstverständlich ohne die Begriffe zu kennen.
Häufig treten jedoch nach seinen Untersuchungen Ebenenverwechslungen (zwischen
Ableitung und Funktion bzw. Bestand und Änderung) auf, insbesondere im Fall von
gegensinniger Kovariation. Mit gegensinniger Kovariation wird der Fall bezeichnet, in dem
der Bestand (Funktion) steigt, die Änderung (Ableitungsfunktion) jedoch abnimmt oder aber
der Fall in dem der Bestand (Funktion) fällt, die Änderung (Ableitungsfunktion) jedoch
zunimmt. Selbst bei Studienanfängern treten nach Hahns Studie hierbei noch viele
Verwechslungen auf.
In seiner Arbeit entwickelte Hahn aus seinen Erkenntnissen zum Vorwissen von Schülern
einen daran angepassten Einstieg in die Differentialrechnung. Dabei werden entsprechend des
Modells der didaktischen Rekonstruktion zwei Ziele verfolgt.
a) Conceptual Change: Vorstellungsänderung, d. h. falsche Vorstellungen bei den Schülern
sollen gelöscht und durch neue ersetzt werden (Hahn bezeichnet dies als vertikale
Vorstellungsentwicklung)
b) Ergänzen zusätzlicher alternativer Vorstellungen (neben den bereits vorhandenen) sowie
situationsangemessene Aktivierung der richtigen Vorstellungen (Hahn bezeichnet dies als
horizontale Vorstellungsentwicklung)
Das Vorgehen im Unterricht stellt er folgendermaßen dar:
Begonnen wird mit einem Beispiel (vergleiche Unterrichtsentwurf unten), in dem
gegensinnige Kovariation auftritt und es somit nötig wird, die Begriffe Bestand und
Änderung genau voneinander abzugrenzen. Daraufhin werden die Begriffe lokaler
Extrempunkt und Wendestellen als Punkte, an denen sich die Qualität des Wachstums ändert
eingeführt. Dies schließt direkt an das Vorwissen der Schüler an, die in der Lage sind, diese
Punkte zu identifizieren. Nun werden sie lediglich mathematisch benannt. Eine exaktere
Definition und auch eine formale Berechnung erfolgt im folgenden Unterricht.
Hahn konnte klare Erfolge dieser Unterrichtssequenz feststellen. Die Schüler machten bei
einem Test weniger Fehler bei der Unterscheidung von Funktion und Ableitung als angehende
Studenten. Dennoch lagen bei gegensinniger Kovariation nur 60% richtig, was nochmals die
Schwierigkeit dieses Sachverhalts deutlich macht.
Zusätzlich zu diesem Einstieg, der auf den conceptual change abzielt, da hier Veränderungen
in der (intuitiv falschen) Vorstellung angestrebt werden, schlägt Hahn vor, auch auf die
Ergänzungen von alternativen Vorstellungen (horizontale Vorstellungsentwicklung)
einzugehen. Nach seinen Untersuchungen gaben die Schüler die Steigung anfangs häufig in
Prozent an. Da diese Vorstellung nicht falsch ist, für den Bereich der Differentialrechnung
jedoch weniger geeignet, besteht hier die Möglichkeit der Gegenüberstellung und der
Diskussion wann welche Vorstellung nützlich ist.
Es soll nun ein möglicher Ablaufplan einer Einführungsstunde skizziert werden, in dem die
Vorstellung der Ableitung als Änderung genutzt und somit gezielt an das Vorwissen der
Schüler angeknüpft werden soll:
Zeit
Lehrertätigk
eit
7
min
Vorstellen
des Graphen
der Umsätze
eines
Supermarktes
18
min
15
min
5
Schülertätigkeit
Aufgabenstellung:
1) Interpretation des
Verlaufs des Graphen
(Aufschreiben von
Fragen)
2) Einteilen in inhaltlich
bedeutsame Phasen
Monitoring
Aufgabenstellung:
des Prozesses 1) Mündliche
in den
Interpretation des
Gruppen,
Graphen (Diskussion
eventuell
untereinander, Klärung/
Hilfestellung Aufschreiben von
Fragen)
2) Einteilen in inhaltlich
bedeutsame Phasen
3) Plakat mit Ergebnissen
erstellen
Zusatzaufgabe für
schnelle Gruppen:
4) Umsatzänderungsgraphen zeichnen
Problematisie Vorstellung der
rung der
Arbeitsergebnisse der
gegensinnige einzelnen Gruppen,
n
Diskussion, eventuell
Kovariation, Vergleich verschiedener
Diskussion
Herangehensweisen, falls
der
nötig Richtigstellung
Probleme, die
entstanden
sind
Benennung der (hoffentlich) von den
Sozialform
Einzela
rbeit
Unterri
chtsmit
tel
OHP,
siehe
unten
Teilziele
jedem Schüler die
Möglichkeit zur
Beschäftigung mit der
Fragestellung geben, bevor
in die Gruppenarbeit
eingestiegen wird (wichtig
für schwache Schüler)
Motivation,
Erfassen des Paradox der
gegensinnigen Kovariation,
Erkennen der Extrema und
Wendepunkte als Stellen, an
denen sich die Qualität der
Änderung ändert
Gruppe
n-arbeit
OHP,
Blatt
mit
großer
Kopie
des
Graphe
n für
jede
Gruppe
,
Plakate
Plenum
Angefe
rtigte
Plakate
Unterscheidung der Begriffe
Bestand und Änderung
Plenum
Tafel
Definition der Begriffe
min
Schülern gefundenen herausragenden
Punkte (Maximum, Wendepunkt),
Entwicklung von Definitionen (Sicherung
im Heft)
Minimum, Maximum und
Wendepunkt mit Hilfe der
Begriffe Bestand und
Änderung (anschauliche
Definition, die später
konkretisiert werden kann)
Abbildung für den OHP:
Bemerkung: In der folgenden Stunde könnte man beispielsweise über CAS (vergleiche
Unterrichtsentwurf 1) den Zusammenhang der Änderungsfunktion und der Umsatzfunktion
nochmals deutlich machen und so auch die Beziehung zwischen „Änderungsgrad“ und
Tangentensteigung diskutieren, so dass man den Schülern verschiedene Zugänge zum Thema
bietet.
Alternativ könnte man in der nächsten Stunde auch beginnen, bestimmte Werte der Änderung
zu berechnen. Dabei kann man von der absoluten Änderung über die mittlere Änderung zur
lokalen Änderung (Ableitung) hinführen. Dies ist durchaus auch mit Hilfe eines grafikfähigen
Taschenrechners oder CAS denkbar, indem die Funktionsgleichung des in dieser
Einführungsstunde behandelten Graphen angegeben wird. Es ist jedoch auch zu überlegen,
hierfür zunächst eine einfachere und besser bekannte Funktion zu verwenden (z.B. Parabel).
Notwendige Vorkenntnisse der Schüler:
- Grundlagenwissen über Funktionen (aus der Mittelstufe): Interpretation von
Funktionsgraphen; Ablesen aus einem Graphen, in welchem Bereich eine Funktion steigt
und fällt; Ablesen von geringer und großer Umsatzsteigerung aus einem Graphen (in dem
Umsatz gegen Zeit aufgetragen ist)
- Vorkenntnisse aus dem Alltag (z.B. konstanter Umsatz bedeutet, dass sich der Umsatz
nicht ändert; sinkender Umsatz bedeutet, dass eine negative Umsatzänderung vorliegt;
eine starke Zunahme/ Steigerung des Umsatzes in einem kurzen Zeitraum bedeutet eine
hohe Änderung des Umsatzes; eine geringe Zunahme des Umsatzes in einem kurzen
Zeitraum bedeutet eine geringe Änderung)
- Fähigkeit zur Gruppenarbeit (Schüler sollten mit Gruppenarbeit vertraut sein)
- Fähigkeit der Erstellung von Plakaten (Grundregeln der Darstellung auf Plakaten)
- Fähigkeiten des Präsentierens (Präsentieren von Ergebnissen sollte vorher geübt worden
sein, z.B. Vorrechnen und Erklären einer Hausaufgabe)
Mögliche Vor- und Nachteile dieses Unterrichtseinstiegs:
Vorteile
- das Vorwissen der Schüler wird gezielt aufgegriffen und genutzt
- falsche Vorstellungen (z.B. zur gegensinnigen Kovariation) werden gezielt angesprochen
und können somit für die Zukunft vermieden werden
- die Schüler arbeiten selbständig am Thema (entdeckendes Lernen)
- die Schüler können sich verschiedene Zugänge erarbeiten (es sind z.B. verschiedene
Einteilungen des Graphen in Phasen möglich)
- Anschluss an Alltagssituationen (Praxisbezug)
- der Lehrer ist lediglich Moderator, nicht bestimmendes Element des Unterrichts
- viele langfristige Ziele werden bei diesem Unterricht mit abgedeckt (siehe unten)
Nachteile
- man kommt in dieser ersten Stunde noch nicht zu mathematisch exakten Begriffen von
Ableitung oder Extremwerten
- hohe Anforderungen an den Lehrer bei der Vorstellung der Ergebnisse, um diese
zusammenzufassen, verschiedene Aspekte herauszuheben und nochmals zu diskutieren
- Problem der Vielfalt der Zugänge, die zum Schluss gebündelt werden müssen
- starke Abhängigkeit von zielführenden Schülerideen; wenn diese nicht kommen, muss der
Lehrer viel vorgeben
- geringere Planbarkeit des Unterrichtsverlaufs (schlecht für unsichere Lehrer)
- in der Gruppenarbeit bringen sich eventuell nicht alle Schüler gleich stark ein
Kurzfristige und längerfristige Ziele, die durch diesen Unterrichtseinstieg angesteuert
werden sollen:
Kurzfristige Ziele:
- Unterscheidung zwischen der Ebene des Bestandes und der Änderung
- Erfassen des Paradox der gegensinnigen Kovariation (insbesondere: Wenn der Bestand
steigt, heißt das nicht automatisch, dass auch die Änderung steigt)
- Erkennen der Extrema und Wendepunkte als Stellen, an denen sich die Qualität der
Änderung ändert
- anschauliche Definition der Begriffe Maximum, Minimum und Wendepunkt
Längerfristige Ziele:
- Sozialkompetenz durch Gruppenarbeit
- mathematisches Kommunizieren und Argumentieren durch die Diskussion in der Gruppe
- Präsentieren (Plakaterstellung und –vorstellung)
Literatur:
Blum, Werner und Kirsch, Arnold: Die beiden Hauptsätze der Differential- und
Integralrechnung in mathematik lehren, Heft 78, S.60-65
Bürger, Heinrich und Malle, Günther: Eine Chance, argumentieren zu lernen in mathematik
lehren, Heft 103, S.60-64
Hahn, Steffen und Prediger, Susanne: Bestand und Änderung – Ein Beitrag zur Didaktischen
Rekonstruktion der Analysis in JMD 29 (2008), Heft 3/4, S.163-198
Schneider, Edith: Einstieg in die Differentialrechnung mit CAS in mathematik lehren, Heft
102, S.40-43
http://www.geogebra.org/de/examples/funktion_steigung/funktion_steigung1.html
http://www.geogebra.org/de/examples/funktion_steigung/funktion_steigung2.html
http://www.geogebra.org/de/examples/funktion_steigung/funktion_steigung3.html
http://www.geogebra.org/de/examples/funktion_steigung/funktion_steigung_projektbeschreib
ung.pdf