Die im Kerncurriculum (KC) aufgeführten prozessbezogenen
Werbung
EdM 11 Einführungsphase Technik Die im Kerncurriculum (KC) aufgeführten prozessbezogenen Kompetenzen „Mathematisch Argumentieren“, „Probleme mathematisch lösen“, „Mathematisch Modellieren“, „Mathematische Darstellungen verwenden“, „Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen“ und „Kommunizieren“, sind in der folgenden Übersicht nicht explizit aufgenommen, da sie die Grundlage eines problemorientierten, schülerzentrierten Mathematikunterrichts darstellen und somit einzelnen Themen nicht eindeutig zuzuordnen sind. Gliederung im Buch 1 Funktionen Lernfeld: Funktionale Zusammenhänge 1.1 Funktionsbegriff – Modellieren von Sachverhalten Inhaltsbezogenen Kompetenzen 1.2 Lineare Funktionen 1.2.1 Begriff der linearen Funktion - Eigenschaften 1.2.2 Gegenseitige Lage von Geraden 1.2.3 Funktionen aus Daten – lineare Regression 1.3 Quadratische Funktionen 1.3.1 Definition - Nullstellen - Linearfaktordarstellung 1.3.2 Scheitelpunktform - Extremwertbestimmung 1.3.3 Bestimmung quadratischer Funktionen 1.4 Ganzrationale Funktionen 1.4.1 Potenzfunktionen mit natürlichen Exponenten 1.4.2 Potenzfunktionen mit negativen ganzen Exponenten 1.4.3 Begriff der ganzrationalen Funktion 1.4.4 Globalverlauf 1.4.5 Symmetrie 1.4.6 Nullstellen ganzrationaler Funktionen - Polynomdivision 1.4.7 Rationale Funktionen in technischen Zusammenhängen 1.5 Exponentialfunktionen und Logarithmus stellen Datenpaare auch unter Verwendung der eingeführten Technologie grafisch dar und führen Regressionen durch. - modellieren Sachsituationen, indem sie die Eigenschaften von Funktionen zur Lösung von Problemen nutzen und die Lösungen bewerten erkennen in Anwendungsbezügen funktionale Zusammenhänge als Zuordnungen zwischen Zahlen bzw. Größen in Tabellen, Diagrammen und Sachtexten, beschreiben diese verbal, erläutern und beurteilen sie - kennen verschiedene symbolische Darstellungsformen für Funktionen identifizieren und klassifizieren Funktionen in Tabellen, Termen, Gleichungen und Graphen und wechseln zwischen den Darstellungen. - nutzen Potenz-, Exponential- und Sinusfunktion als Mittel zur Beschreibung quantitativer Zusammenhänge führen eine Parametervariation für Potenz- und Exponentialfunktionen in der Form y a f b x cd an Beispielen unter Verwendung der eingeführten Technologie durch und beschreiben und begründen die Auswirkung auf den Graphen. grenzen in Sachzusammenhängen lineares und 1 EdM 11 Einführungsphase Technik 1.5.1 Exponentielles Wachstum 1.5.2 Exponentialfunktionen - Eigenschaften 1.5.3 Verschieben und Strecken der Graphen der Exponentialfunktionen 1.5.4 Lösen von Exponentialgleichungen - Logarithmus 1.5.5 Exponential- und Logarithmusfunktionen in technischen Zusammenhängen 1.6 Trigonometrische Funktionen 1.6.1 Sinus, Kosinus und Tangens im rechtwinkligen Dreieck (Wdh.) 1.6.2 Sinus und Kosinus am Einheitskreis 1.6.3 Bogenmaß eines Winkels 1.6.4 Definition und Eigenschaften der Sinusfunktion 1.6.5 Strecken des Graphen der Sinus- und Kosinusfunktion 1.6.6 Verschieben der Graphen der Sinus- und Kosinusfunktion 1.6.7 Allgemeine Sinusfunktion 1.6.8 Anwenden und Modellieren mit allgemeinen Sinusfunktionen Kompetenzcheck 2 Differenzialrechnung Einstiegsseite Differenzialrechnung Lernfeld: Änderungen beschreiben 2.1 Tangentensteigung und Änderungsrate – Ableitung 2.1.1 Steigung eines Funktionsgraphen in einem Punkt - Ableitung 2.1.2 Lokale Änderungsrate 2.1.3 Ableitung der Quadratfunktion Brennpunkteigenschaft 2.1.4 Ableitung weiterer Funktionen 2.2 Differenzierbarkeit – Ableitungsfunktion 2.2.1 Differenzierbarkeit Blickpunkt: Stetigkeit und Differenzierbarkeit 2.2.2 Ableitungsfunktion 2.2.3 Ableitung der Sinus- und Kosinusfunkton 2.3 Ableitungsregeln 2.3.1 Faktorregel 2.3.2 Summenregel 2.4 Differenzialrechnung in technischen Anwendungen exponentielles Wachstum gegeneinander ab, auch unter Verwendung der eingeführten Technologie - deuten in grafischen Darstellungen von Anwendungssituationen die Parameter der Potenz- und Exponentialfunktion bestimmen eine Funktionsgleichung aus gegebenem Graphen für Potenz- und Exponentialfunktion in der Form y a f b x cd. - beschreiben und interpretieren mittlere Änderungsraten und Sekantensteigungen in funktionalen Zusammenhängen, die als Tabelle, Graph oder Term dargestellt sind, berechnen diese auch unter Verwendung der eingeführten Technologie und erläutern sie an Beispielen - beschreiben und interpretieren mithilfe eines propädeutischen Grenzwertbegriffs die Entwicklung der Ableitung als lokale Änderungsrate aus der mittleren Änderungsrate - beschreiben und interpretieren die Ableitung als Tangentensteigung, erläutern sie an Beispielen und berechnen sie unter Verwendung des eingeführten Taschenrechners - entwickeln Graph und Ableitungsgraph auseinander, beschreiben und begründen Zusammenhänge und interpretieren diese in Sachzusammenhängen - kennen zur Bildung der Ableitungsfunktion die Potenzregel, Faktorregel und Summenregel und wenden diese zur Berechnung der Ableitungsregeln von ganzrationalen Funktionen an - kennen die Ableitungsfunktion von x → sin (x) 2 EdM 11 Einführungsphase Technik Kompetenzcheck 3 Fortführung der Differenzialrechnung Lernfeld: Auf und ab, hin und her 3.1 Änderungsverhalten von Funktionen 3.1.1 Extrema und Monotonie 3.1.2 Untersuchung auf Monotonie und Extrema mithilfe der 1. Ableitung 3.1.3 Das NEWTON-Verfahren zur Bestimmung von Nullstellen 3.2 Linkskurve, Rechtskurve – Wendepunkte – 2. Ableitung 3.3 Kriterien für –Extrem- und Wendepunkte 3.3.1 Kriterien für Extremstellen 3.3.2 Kriterien für Wendestellen 3.3.3 Anwenden der Kriterien zur Untersuchung von Funktionen 3.4 Extremwertaufgaben 3.5 Weitere technische Anwendungen der Differenzialrechnung Kompetenzcheck - beschreiben und begründen Zusammenhänge zwischen Graph und Ableitungsgraph auch unter Verwendung der Begriffe Extrem- und Wendepunkt - lösen mit der Ableitung Sachprobleme mit Anwendungsbezug, auch unter Verwendung der eingeführten Technologie lösen mit der Ableitung von ganzrationalen Funktionen bis 4. Grades Optimierungsprobleme, auch unter Verwendung der eingeführten Technologie 3
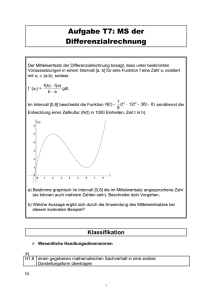







![für eine stetige Funktion f e C[a,b] Um das Polynom pd(x) von Grad](http://s1.studylibde.com/store/data/010375789_1-5deb84f41ff930e9273ba618f926d47b-300x300.png)

