1 Negative Zahlen

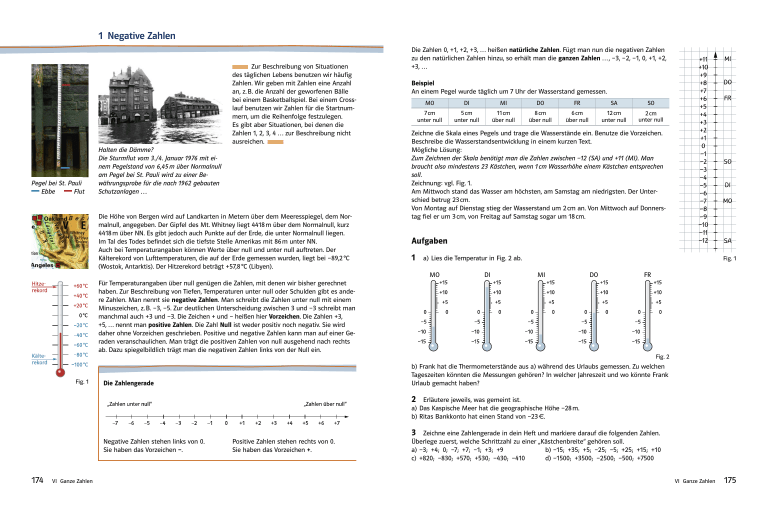
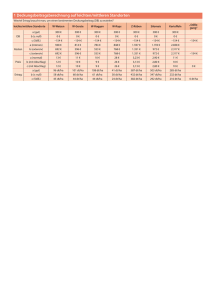
1 Negative Zahlen
Zur Beschreibung von Situationen
des täglichen Lebens benutzen wir häufig
Zahlen. Wir geben mit Zahlen eine Anzahl
an, z. B. die Anzahl der geworfenen Bälle
bei einem Basketballspiel. Bei einem Crosslauf benutzen wir Zahlen für die Startnummern, um die Reihenfolge festzulegen.
Es gibt aber Situationen, bei denen die
Zahlen 1, 2, 3, 4 . . . zur Beschreibung nicht
ausreichen.
Pegel bei St. Pauli
Ebbe
Flut
Halten die Dämme?
Die Sturmflut vom 3./4. Januar 1976 mit einem Pegelstand von 6,45 m über Normalnull
am Pegel bei St. Pauli wird zu einer Bewährungsprobe für die nach 1962 gebauten
Schutzanlagen . . .
Die Höhe von Bergen wird auf Landkarten in Metern über dem Meeresspiegel, dem Normalnull, angegeben. Der Gipfel des Mt. Whitney liegt 4418 m über dem Normalnull, kurz
4418 m über NN. Es gibt jedoch auch Punkte auf der Erde, die unter Normalnull liegen.
Im Tal des Todes befindet sich die tiefste Stelle Amerikas mit 86 m unter NN.
Auch bei Temperaturangaben können Werte über null und unter null auftreten. Der
Kälterekord von Lufttemperaturen, die auf der Erde gemessen wurden, liegt bei –89,2 °C
(Wostok, Antarktis). Der Hitzerekord beträgt +57,8 °C (Libyen).
Die Zahlen 0, +1, +2, +3, . . . heißen natürliche Zahlen. Fügt man nun die negativen Zahlen
zu den natürlichen Zahlen hinzu, so erhält man die ganzen Zahlen . . . , –3, –2, –1, 0, +1, +2,
+3, . . .
Beispiel
An einem Pegel wurde täglich um 7 Uhr der Wasserstand gemessen.
MO
DI
MI
DO
FR
SA
SO
7 cm
unter null
5 cm
unter null
11 cm
über null
8 cm
über null
6 cm
über null
12 cm
unter null
2 cm
unter null
Zeichne die Skala eines Pegels und trage die Wasserstände ein. Benutze die Vorzeichen.
Beschreibe die Wasserstandsentwicklung in einem kurzen Text.
Mögliche Lösung:
Zum Zeichnen der Skala benötigt man die Zahlen zwischen –12 (SA) und +11 (MI). Man
braucht also mindestens 23 Kästchen, wenn 1 cm Wasserhöhe einem Kästchen entsprechen
soll.
Zeichnung: vgl. Fig. 1.
Am Mittwoch stand das Wasser am höchsten, am Samstag am niedrigsten. Der Unterschied betrug 23 cm.
Von Montag auf Dienstag stieg der Wasserstand um 2 cm an. Von Mittwoch auf Donnerstag fiel er um 3 cm, von Freitag auf Samstag sogar um 18 cm.
Aufgaben
1
a) Lies die Temperatur in Fig. 2 ab.
MO
DI
Fig. 1
MI
Für Temperaturangaben über null genügen die Zahlen, mit denen wir bisher gerechnet
haben. Zur Beschreibung von Tiefen, Temperaturen unter null oder Schulden gibt es andere Zahlen. Man nennt sie negative Zahlen. Man schreibt die Zahlen unter null mit einem
Minuszeichen, z. B. –3, –5. Zur deutlichen Unterscheidung zwischen 3 und –3 schreibt man
manchmal auch +3 und –3. Die Zeichen + und – heißen hier Vorzeichen. Die Zahlen +3,
+5, . . . nennt man positive Zahlen. Die Zahl Null ist weder positiv noch negativ. Sie wird
daher ohne Vorzeichen geschrieben. Positive und negative Zahlen kann man auf einer Geraden veranschaulichen. Man trägt die positiven Zahlen von null ausgehend nach rechts
ab. Dazu spiegelbildlich trägt man die negativen Zahlen links von der Null ein.
Fig. 1
DO
FR
Fig. 2
b) Frank hat die Thermometerstände aus a) während des Urlaubs gemessen. Zu welchen
Tageszeiten könnten die Messungen gehören? In welcher Jahreszeit und wo könnte Frank
Urlaub gemacht haben?
Die Zahlengerade
2
Erläutere jeweils, was gemeint ist.
a) Das Kaspische Meer hat die geographische Höhe –28 m.
b) Ritas Bankkonto hat einen Stand von –23 €.
3
Negative Zahlen stehen links von 0.
Sie haben das Vorzeichen –.
174
VI Ganze Zahlen
Positive Zahlen stehen rechts von 0.
Sie haben das Vorzeichen +.
Zeichne eine Zahlengerade in dein Heft und markiere darauf die folgenden Zahlen.
Überlege zuerst, welche Schrittzahl zu einer „Kästchenbreite“ gehören soll.
a) –3; +4; 0; –7; +7; –1; +3; +9
b) –15; +35; +5; –25; –5; +25; +15; +10
c) +820; –830; +570; +530; –430; –410
d) –1500; +3500; –2500; –500; +7500
VI Ganze Zahlen
175