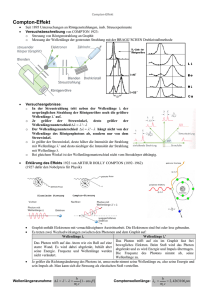
Compton Effekt

Der Compton-Effekt
Der Compton-Effekt
Einleitung
1921 untersuchte Arthur Holly Compton die Streuung von Röntgenstrahlen an Graphit und
anderen Elementen bei denen die Elektronen schwach gebunden sind. Dabei beobachtete er bei
der Streuung von Röntgenstrahlen eine Wellenlängenverschiebung und dass zusätzlich zur
spektral unverschobenen Streustrahlung der ursprünglichen Wellenlänge 1 noch eine
spektralverschobene Komponente der Wellenlänge 2 auftritt.
Die Wellenlängenverschiebung ´ -  ist abhängig vom Streuwinkel  aber unabhängig vom
Streumaterial.
c
1
cos
mit der so genannten Compton
h
12
2.43 x10
m
c
mc
Wellenlänge
Vom Streumaterial hängt nur die Intensität
der Compton-Streuung ab, die bei leichten
Materialien besonders groß ist. Die Wellenlängenverschiebung ´ -  ist maximal bei

= 180 und ist unabhängig von einlaufenden Wellen.
h
´
mc
. 1
cos
Compton-Streuung
Diese Versuchergebnisse konnten mit den klassischen Ansätzen der Physik nicht erklärt
werden, und so forschte Compton bis 1923, wo er die Streuung der Strahlen anhand eines
Lichtteilchens zu erklären versuchte:
Er betrachtete den Compton-Effekt als einen zwischen einem Photon und einem anfangs
ruhendem freien Elektronen, bei dem sowohl Energie- als auch Impulssatz erfüllt sein müsse.
Energiesatz:
h
h ´
1
mc²
1
1
v²
c²
Seite 1
14.05.2016
Der Compton-Effekt
Impulssatz:
h
c
h ´
mv
c
1
v²
c²
Aus der ersten Gleichung folgt unmittelbar, das  >´ ist, das heißt das Photon gibt bei der
Streuung Energie an das Elektron ab und hat nach der Streuung folglich eine größere
Wellenlänge.
Aus diesen Überlegungen lässt sich der Schluss ziehen, dass ein freies Elektron das Licht nicht
absorbieren kann, sondern nur streuen. Eine völlige Absorption würde bedeuten das  ´=0 und
 ´/ c=0 sind. Die Forderung nach gleichzeitiger Erhaltung von Energie und Impuls verbietet
die Absorption eines Lichtquants an einem ruhenden Elektron ebenso wie für ein gleichförmig
bewegtes Elektron. Man kann nämlich aufgrund des Kovarianzprinzips immer ein
Bezugssystem wählen, relativ zu dem das einfallende Elektron ruht. Die Unmöglichkeit der
Absorption darf aber nicht vom Bezugssystem abhängen. Aus Symmetriegründen gilt die
gleiche Schlussforderung auch für die Emission eines Lichtquants. Ein gleichförmig bewegtes
Elektron kann aus Gründen der gleichzeitigen Energie- und Impulserhaltung kein Lichtquant
emittieren und strahlt daher nicht.
Klassische Erwartung im Vergleich zum experimentellen Ergebnis
Seite 2
14.05.2016
Der Compton-Effekt
Physikalisch theoretische Voraussetzungen

Einstein´sche Theorie vom Licht als Photonen (Quanten), die sich mit der Energie h·ν
und der Lichtgeschwindigkeit c bewegen.

Energie einer bewegten Masse:
m0
E = m·c2
mit der
Masse
(m0 ist die Ruhemasse, v die
m=
√ (1-(/) )
v

c
Geschwindigkeit)
2
Masse eines Photons:
h·ν
E = h·ν = m·c2
⇒
m=
c2

Impuls eines Photons:
h·ν
p=
c
Superposition des Impulses p = m·v bei einem Stoßvorgang.
Seite 3
14.05.2016
Der Compton-Effekt
Berechnung des Compton-Effekts
Schematische Darstellung des Compton-Effekts
Berechnung über 4-Impuls
Einlaufendes Photon:
Ruhendes Elektron:
Auslaufendes Photon:
Auslaufendes Elektron:
ep=(h  ,h / c,0,0)
re=(m c²,0,0,0)
ap=(h  ´,h  ´.cos / c, h  ´.si n / c,0 )
ep=(h  -h ´+m c²,h  /c-h ´.cos / c,h  / c-h ´.si n / c ,0 )
Die sogenannten 4-Impulse sind vierkomponentige Vektoren. Die erste Komponente ist die
Energie des Teilchens, die anderen drei sind die Impulskomponenten.
Impulse gleichzeitig ein- und auslaufender Teilchen addieren sich Komponentenweise. Der
gesamte einlaufende 4-Impuls muss gleich sein wie der gesamte auslaufende 4-Impuls.
Das „Quadrat“ des Impulses wird vom Vektorquadrat abweichen.
Falls p=(E,p 1 ,p 2 ,p 3 ) dann folgt daraus p² =E² - c²(p1²+p2²+p3² )=E² - c²p²
Für einzelne Teilchen gilt: E²-c²p²=m ²c4
Das einlaufende Elektron hat die Masse m und das einlaufende Photon besitzt Masse 0.
Das Photon nähert sich dem Elektron in Richtung der positiven X-Achse. Es wird erwartet das
sich das Photon mit dem Winkel  bezüglich zur X-Achse wieder vom Elektron entfernt. Da
die Masse des Photons unverändert 0 ist, können wir die Y-Achse so wählen dass das Photon
den oben angeführten 4-Impuls besitzt.
Damit der Impuls der auslaufenden Teilchen gleich bleibt wie der der Einlaufenden, muss das
gestreute Elektron den bereits genannten Impuls besitzen. Das „Quadrat“ des Impulses muss
m²c4 sein, da es sich hierbei um ein Elektron handelt:
Seite 4
14.05.2016
Der Compton-Effekt
ea ²
h
4
m²c
h ´
me c²
2 h .h ´
h ´ ²
h ´ ²cos ²
h
h ´
c
c
2 h c²me
cos
2 h ´c²m
4
h ´ c m²
h ´ mc²
h ´
c²
4
c m
2 h .h ´cos
h ´ mc² 2 h .h ´cos
1
h ´ ²sin
2 h .h ´cos
h ´ ²sin ²
2 h .h ´ 2 h
2 h
h
c²
4
m²c
4
m²c
2 h .h ´
h .h ´ 1 cos
1
1
h
mc²
1
cos
Wenn man für die Wellenlänge folgende Beziehung einsetzt
c
erhält man als Ergebnis
´
h
mc
1 cos
die Gleichung für den Compton
,
Effekt
Zum besseren Verständnis des Compton-Effekts:

Die Compton-Streuung ist verhältnismäßig schwach bei stark gebundenen Elektronen,
das heißt in schweren Atomen. Wenn die Bindungsenergie der Elektronen groß gegen
die Quantenenergie h der Photonen ist, dann ist kein Impulsübertrag möglich

Der Compton-Effekt ist in bestimmten Energiebereichen, und zwar für mittelharte
Röntgenstrahlen, der für die Streuung und Abschwächung von Röntgenstrahlen in
Materie wichtigste physikalische Vorgang

Bei der Streuung mit h´≠ h sind einfallende und gestreute Strahlung zueinander
inkohärent
Seite 5
14.05.2016
Der Compton-Effekt
Wie wir sehen, können der Photoeffekt und der Compton-Effekt nur so verstanden werden,
dass das Licht aus einzelnen Teilchen mit einem Impuls p besteht. Andererseits wissen wir aus
Interferenz- und Beugungsexperimenten, das sich Licht wie eine Welle verhält, die durch eine
Wellenlänge  und eine Frequenz  charakterisiert ist. Die Teilcheneigenschaften des Lichtes
haben durch Photo- und Compton-Effekt ihre Begründung gefunden.
Wie ist nun Wellen- und Teilchencharakter miteinander vereinbar? Zur Klärung dieser Frage
stellen wir uns in Gedanken folgendes Experiment vor:
Durch eine Blende mit einem sehr kleinen Loch lassen wir einen Lichtstrahl auf einen Schirm
fallen. Auf diesem Schirm beobachtet man nach der Wellenoptik eine Beugungsfigur.
Entsprechend könnte man das Licht hinter dem Schirm durch den Compton-Effekt oder durch
den Photoeffekt nachweisen. Macht man nun die Intensität des Lichtes immer kleiner und
kleiner, so stellt man anhand etwa des Photoeffekts fest, dass ganz lokal, an irgendeiner Stelle,
jeweils ein Photo-Elektron vom Licht losgeschlagen wird. Es offenbart sich also der
Teilchencharakter. Wiederholt man nun dieses Experiment sehr oft und registriert die
Häufigkeit, mit der der Photoeffekt an den einzelnen Stellen vorkommt, so ergibt sich eine
Häufigkeitskurve, die genau mit dem Beugungsbild übereinstimmt.
Dieses Gedankenexperiment, das man durch tatsächliche Experimente ausführen könnte, liefert
den Schlüssel zur Deutung der Natur des Lichts. Das Licht trägt, sozusagen virtuell, beide
Eigenschaften – Welle und Korpuskeln in sich. Je nach dem durchgeführten Experiment zeigt
es die eine oder die andere Natur. Um beide, zunächst widersprüchlichen Aspekte zu vereinen,
muss eine statistische Betrachtungsweise angewandt werden. Im vorliegenden Fall also, wenn
wir ein Experiment machen, das die Beugungsfigur nachweisen soll, dann aber doch nach dem
Korpuskelcharakter fragen, können wir nicht mehr mit Sicherheit den Auftreffpunkt des
Lichtteilchens voraussagen. Wir können viel mehr nur die Wahrscheinlichkeit dafür angeben,
dass es an einem bestimmten Punkt auftrifft. Diese Wahrscheinlichkeitsverteilung ist dann
identisch mit der nach der klassischen Physik berechneten Beugungsfigur. Diese statistische
Betrachtungsweise ist grundlegend für eine quantentheoretische Deutung der Phänomene.
Seite 6
14.05.2016