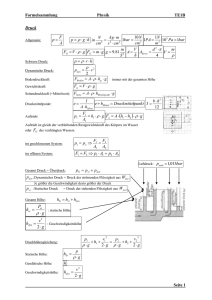
1 Zustandsgrössen und System
Werbung

Formelsammlung
Thermo- und
Hydrodynamik
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
Inhaltsverzeichnis
1
1.1
Zustandsgrössen und System .................................................. 3
Systembegriff, Systemgrenzen ................................................................... 3
1.1.1
1.1.2
1.2
Zustands- und Prozessgrössen .................................................................. 4
1.2.1
1.3
Spezifische Zustandsgrössen ........................................................................................... 4
Thermische Zustandsgleichung .................................................................. 4
1.3.1
1.3.2
1.3.3
1.3.4
1.4
Stationär / Instationär ........................................................................................................ 3
Spezielle Systeme ............................................................................................................ 3
Ideale Gasgleichung ......................................................................................................... 4
Realgasfaktor .................................................................................................................... 5
Verschiedenes .................................................................................................................. 5
Gasgemische .................................................................................................................... 5
Kalorische Zustandsgleichung.................................................................... 6
1.4.1
1.4.2
Äquipartitionsgesetz von Boltzmann ................................................................................ 6
Spezifische Wärmekapazität ............................................................................................ 6
2
Massen- und Energieerhaltung ................................................. 7
2.1
2.2
Massenerhaltung: Kontinuitätsgleichung .................................................. 7
Energieerhaltung: 1. Hauptsatz ................................................................... 7
2.2.1
2.2.2
2.2.3
2.3
2.4
Geschlossenes System .................................................................................................... 7
Offenes-, oder massedurchflossenes System .................................................................. 8
Allgemeiner 1. Hauptsatz für offene Systeme .................................................................. 9
Eindimensionale Bernoulli-Gleichung ........................................................ 9
Druckverluste ................................................................................................ 9
2.4.1
Gerades Rohrstück ........................................................................................................... 9
3
Reale Effekte ............................................................................ 10
3.1
3.2
3.3
Quergleichung ............................................................................................ 10
Grenzschicht ............................................................................................... 10
Rohrströmung ............................................................................................. 10
3.3.1
3.3.2
3.3.3
3.3.4
3.4
Reversible und irreversible Vorgänge, Zustandsgrösse Entropie ......... 11
3.4.1
3.4.2
3.4.3
3.4.4
3.4.5
3.5
3.6
3.7
3.8
Reversible und irreversible Vorgänge ............................................................................ 11
Gibb’sche Hauptgleichung: ............................................................................................. 11
Isentropenexponent ........................................................................................................ 11
Isentropengleichung (Zusammenhang der ZGr bei konstanter Entropie ) ..................... 12
Spezifische Arbeit bei konstanter Entropie ..................................................................... 12
Der 2. Hauptsatz.......................................................................................... 12
Das T-S-Diagramm...................................................................................... 13
Der 3. Hauptsatz, Nernst’sches Wärmetheorem ...................................... 13
Kreisprozesse ............................................................................................. 13
3.8.1
3.8.2
3.9
Einlaufstrecke ................................................................................................................. 10
Parabolisches Geschwindigkeitsprofil ............................................................................ 10
Turbulentes Geschwindigkeitsprofil ................................................................................ 10
Nicht-kreisrunde Strömungskanäle................................................................................. 10
Kreisprozessanalyse ....................................................................................................... 13
Wirkungsgrad Joule-Prozess .......................................................................................... 14
Realer Kreisprozess am Beispiel Gasturbine........................................... 15
3.9.1
14.05.2016
Totalenthalpie-Zustände im Gasturbinen-Prozess ......................................................... 15
2 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
1 Zustandsgrössen und System
1.1
Systembegriff, Systemgrenzen
Eine thermodynamische Aussage bezieht sich immer auf ein bestimmtes, exakt
umgrenztes materielles Gebilde, das thermodynamische System. Die Abgrenzung
muss nicht unbedingt körperlich sein. Sie kann auch gedacht sein. Die Abgrenzung
muss allerdings in jedem Fall geschlossen sein.
Bilanzieren:
1.
2.
3.
Massenbilanz:
m1 m2 m3
dm
dt Bilanzgebi et
dm
dt
kg
s
Energiebilanz:
dE
E 1 E 2 E 3
dt Bilanzgebi et
dE
dt
kJ
s
.
Bilanzgebiet:
Massenbilanz:
Energiebilanz:
.
.
abgrenzen durch Wahl der Systemgrenze
Bilanzierung der Massenströme
Bilanzierung der Energieströme
Konvention: Dem System zugeführt = positiv, vom System abgeführt = negativ
1.1.1 Stationär / Instationär
Bei Systemen mit zeitlich unveränderlichen Grössen wird die zeitliche Ableitung zu Null.
Stationär:
1.1.2
0
t
Instationär:
0
t
Wi kJ
Qi kW
Spezielle Systeme
Systembezeichnung
offen
geschlossen
kg
mi
mi kg
s
0
0
Wi kW
Beliebig
Beliebig
Beliebig
Beliebig
Adiabat (perfekte
Isolierung)
Beliebig
Beliebig
0
diabat / diatherm
(unendlich guter
Wärmeleiter)
Beliebig
Beliebig
0
0
0
0
abgeschlossen
14.05.2016
3 / 16
Qi kJ
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
1.2
Zustands- und Prozessgrössen
Natürliche Zustandsgrössen:
Abgeleitete Zustandsgrössen:
Direkt messbare Grössen (Volumen V, Druck p, usw.)
Nicht direkt messbare Grösse (z. Bsp. Energieinhalt E)
1.2.1 Spezifische Zustandsgrössen
Masseabhängige Zustandsgrössen (extensiv):
Masseunabhängige Zustandsgrössen (intensiv):
Volumen V, Dichte ρ, spezif. innere Energie,…
Druck p, Temperatur T
Man kann ein Teilsystem erzeugen, welches genau 1kg Masse enthält und die Probleme könne auf
1kg Masse bezogen werden. Pro Masse normierte Grössen nennt man spezifische Grössen
Spezifisches Volumen:
v
V
m
v
m3
kg
Spezifische Dichte:
m
V
kg
m3
Spezifisches molares Volumen:
V
v~
n
v~
m3
kmol
Spezifische molare Dichte:
n
~
V
~
kmol
m3
Spezifisches innere Energie:
u
U
m
u
kJ
kg
Spezifische Enthalpie:
h
H
m
h
kJ
kg
Spezifisches kinetische Energie:
Ekin w 2
m
2
E kin
m
kJ
kg
Thermische Zustandsgrössen:
Kalorische Zustandsgrössen:
Prozessgrössen:
1.3
Temperatur T, Druck p, spezifisches Volumen v
Enthalpie h, Innere Energie u
Arbeit W, Wärme Q, Strömungsgeschwindigkeit w
Thermische Zustandsgleichung
Die thermische Zustandsgleichung beschreibt den Zusammenhang zwischen den thermischen
Zustandgrössen Druck, Volumen und Temperatur
1.3.1
Ideale Gasgleichung
Avogadro-Konstante:
1mol 6.02 10 23 [Teilchen ]
Universelle Gaskonstante:
J
8314.41
kmol K
p V n T m R T
14.05.2016
p~
v T
4 / 16
R
J
M kg K
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
1.3.2 Realgasfaktor
Bei extremen Bedingungen, z. Bsp. bei sehr hohen Drucken oder bei sehr hohen oder sehr tiefen
Temperaturen, stellt man fest, dass Gase, die bei Umgebungstemperatur die Gasgleichung erfüllen,
Abweichungen von der idealen Gasgleichung aufweisen. Gase mit diesem Verhalten werden reale
Gase genannt. Die thermische Zustandgleichung wird nun reale Gasgleichung (in spezieller Form)
genannt.
z ( p, T )
p V z ( p, T ) m R T
Rreal
Rideal
z(p,T) wird Realgasfaktor genannt
1.3.3 Verschiedenes
Normzustände:
Normdruck:
p 760 [Torr] = 1.01325 [bar]
Normtemperatur: T 0°C
Normvolumen:
vn
Wassersäule:
22.414
m3
kmol
1 [mmWs] = 9.81 [Pa]
In den Diagrammen finden wir immer wieder
ISO-Linien. Das sind Linien mit konstanten
Werten einer Zustandsgrösse.
1.3.4
=
=
=
=
=
=
konstant
konstant
konstant
konstant
konstant
konstant
Isothermen
Isobaren
Isochoren
Isenthalpen
Linien gleicher innerer Energie
Isentropen
Gasgemische
Vi
n
p
mi M i
i i
Vtot ntot ptot mi M i
RGemisch
T
p
v
h
u
s
mi
1
Ri
ni
i mtot
Mi
i ntot
f Gemisch,theoretisch
14.05.2016
n
fi i
ntot
i
Massenanteil:
wi
mi
mtot
Molanteil:
yi
ni
ntot
Volumenanteil:
i
Vi
Vtot
Druckanteil (mit Partialdruck pi):
xi
pi
ptot
5 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
1.4
Kalorische Zustandsgleichung
Zusammenhang zwischen Teilchenverhalten im System und Systemdruck kinetische Gastheorie
Annahmen:
Teilchen fliegen mit Schwirrgeschwindigkeit w’ im Raum
Teilchen nehmen wenig Volumen im System ein „materiell grosse Leere“
Die Reflexionen bei Zusammenstössen der Teilchen mit Gefässwänden und untereinander sind
ideal (vollkommen elastisch und verlustfrei)
keine An- oder Abstossungskräfte unter den Teilchen und zwischen Teilchen und Wand
Häufigste Schwirrgeschwindigkeit:
wh ' 2 R T
1.4.1 Äquipartitionsgesetz von Boltzmann
Die innere Energie U eines thermodynamische Systems besteht in der Summe der dem System
zugeführten Energiemengen (Austausch mit der Umgebung).
Spezifische innere Energie:
f
w'2
u R T
2
2
J
kg
Durch rechnerische Verknüpfung von Zustandsgrössen können weitere Zustandsgrössen definiert
werden. Die Enthalpie verknüpft die Zustandsgrössen U, p und V.
Spezifische Enthalpie:
Beispiele:
aber z.B.:
f
h u p v 1 R T
2
Helium
1-atomig
f=3
Sauerstoff
2-atomig
f=5
CO2 (100 K)
3-atomig
f=5
CO2 (1800 K)
f = 12
NH3 (373 K)
f = 7,2
Luft
f=5
J
kg
1.4.2 Spezifische Wärmekapazität
Es hat sich eingebürgert, dass an Stelle von den Freiheitsgraden f eine Kombination mit f dargestellt
wird, die als Stoffwerte cv (spezifische Wärmekapazität bei konstantem Volumen) und c p (spezifische
Wärmekapazität bei konstantem Druck) bezeichnet werden:
spezifische Wärmekapazität bei konstantem Volumen:
f
cv R
2
spezifische Wärmekapazität bei konstantem Druck:
f
c p 1 R
2
cp c v p v
1
R
T
u u u
f
R (T T ) cv (T T )
2
f
h h h 1 R (T T ) cv (T T )
2
14.05.2016
6 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
2 Massen- und Energieerhaltung
2.1
Massenerhaltung: Kontinuitätsgleichung
m
t Stromröhre
Allgemeine Kontinuitätsgleichung:
w A w A
Für stationäre Strömung:
w A w A 0
Für stationäre Strömung:
w A w A 0
2.2
Energieerhaltung: 1. Hauptsatz
In diesem fundamentalen Satz müssen alle Energieformen (potentielle, kinetische,
Druck-, innere Energie; aber auch magnetische, chemische und elektrische Energie)
elektrische, ...) berücksichtigt werden.
In der Fluiddynamik ist die Energieerhaltung unter dem Namen Bernoulli-Gleichung besser bekannt.
2.2.1 Geschlossenes System
(System ohne Massendurchfluss)
Energieerhaltung:
USy stem WSy stemUmgebung QSy stemUmgebung
dUSy stem
dt mSy stem u u
USy stem
dt
WSystemUmgebung W Fa ds p dV m p dv
Q Sy stemUmgebung Q Q dt
u: spez. innere
Energie
J
kg
Q: Wärmemenge
W: Arbeit
J
Q : Wärmefluss
J
s ;W
W wird auch als W V (Volumenänderungsarbeit) bezeichnet.
Der Wärmefluss Q wird von einem Fluid oder Körper ausserhalb der Systemgrenze mit dem
Systeminneren ausgetauscht.
Im Gegensatz dazu ist der Strahlungs-Wärmefluss Q
Energietransport durch Wellen erfolgt.
14.05.2016
7 / 16
Str unabhängig
von der Materie, da der
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
2.2.2
Offenes-, oder massedurchflossenes System
Die Energie eines Körpers kann in Form von mechanischer (potentieller und kinetischer), thermischer
(innere Energie) und chemischer Energie vorliegen. In der Energiebilanz müssen wir die Veränderung
der Energie im Bilanzgebiet den zu- bzw. abgeführten Energieformen gleichsetzen:
E
Sy stemv olumen
E
therm
Sy stemv olumen
Epot Ekin
w 2
m u g z 2
Sy stemv olumen
Konvektiver Energiefluss: Übertragene Energieströme durch die Systemgrenzen (Massenfluss vom
Eingang bis Ausgang)
w2
Ekonv
m h
2
kg J J
s kg s W
nicht-konvektiver Energieflüsse: Dem System kann Energie pro Zeiteinheit in Form von Leistung,
Druckkräften, Schubspannungskräften und Feldkräften zugeführt werden.
Leistung von Normalkräften oder Druckkräften W*p, dem System von aussen durch bewegte
Flächen (Geschwindigkeit wk) zugeführt.
Wp Fa w k p A Sy stem w k p
Sys tem
Kompression: dV 0 W
VSy stem
t
W W p m w m vdp
0
Expansion:
Sy stem
dV 0 W
0
Mechanische Leistung von Wellen W*W, wird dem System über rotierende Wellen zugeführt.
Leistung von Feldkräften W*f, entstehen, weil Feldkräfte im Systeminneren an den bewegten
Fluidteilchen angreifen. Mögliche Kräfte sind Gravitation, Magnetfeld, elektrostatische Kräfte,
Zentrifugalkräfte und Corioliskräfte.
0
mit Erdfeld f 0
g
dW dFf w dm f w dV f w
f
14.05.2016
8 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
Einschiebe- und Ausschiebearbeit, Verschiebungen der Massen über die Systemgrenzen
bedingen eine Arbeit.
Einschiebearbeit:
Wp,Ein p v m
Einschiebeleistung:
Ausschiebearbeit:
Wp,A us p v m
Ausschiebeleistung:
Wp,Ein Fp ,Ein w p v m
Wp, A us Fp , A us w p v m
Diese Arbeiten sind für einen bestimmten Massenstrom m i mit dem letzten Term im 1.Hauptsatz
verknüpft.
2.2.3
Allgemeiner 1. Hauptsatz für offene Systeme
Kompression Wellen
Feldkräfte
Wärmefluss
konvektiver Term
w 2
w 2
m
u
g
z
W
W
W
Q
m
h
p w g
t Systemvolumen
2 Ab
2
Aw
V
A
Am
Ab
V
Am
2.3
Bewegte Systeme
Systemvolumen
Massedurchströmte Systemgrenze
Aw
A
Welle durch Systemgrenze
Fläche
Eindimensionale Bernoulli-Gleichung
Aus der Energieerhaltungsgleichung kann die Bernoulligleichung hergeleitet werden. Sie wird in 3
verschiedenen Formen dargestellt:
2
2
Energieform:
w
w
1
1
p g z ePumpe p g z eVerluste
2
2
Druckform:
w
w
p g z p Pumpe( zugeführt) p g z pVerluste
2
2
Höhenform:
w
w
1
1
p z H Pumpe
p z H Verluste
2 g g
2 g g
2
2
2
2.4
2.4.1
2
Druckverluste
Gerades Rohrstück
p
p
2
2
14.05.2016
w2
w2
L
d
λ [-] ist die Rohrreibungszahl (Bohl Seite 164 / 165)
ζ [-] ist der Druckverlustbeiwert (Bohl Seite 180)
9 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
3 Reale Effekte
3.1
Quergleichung
Druckverteilung senkrecht zu den Stromlinien für Strömungen mit
Krümmung.
3.2
2
w
p
r 2
r
r
Grenzschicht
Als Grenzschicht wird eine dünne Schicht um einen umströmten Körper bezeichnet. Durch die
Zähigkeit des Fluids werden Schubkräfte übertragen. Das Fluid hat an einer Wand die
Wandgeschwindigkeit w = 0.
kg
Pas
m s
Dynamische Viskosität
Kinematische Viskosität
s
3.3
m2
Werte für und entnimmt man Tabellenbüchern
(VDI-Wärmeatlas, Wasserdampftafel, Dubbel)
oder berechnet sie mit Hilfe von
Gebrauchsformeln
Rohrströmung
3.3.1 Einlaufstrecke
Die bisherigen Berechnungen des Druckverlustes für Rohrleitungen und Rohrabschnitten gelten nur
für Rohrabschnitte, in denen die Geschwindigkeitsprofile voll ausgebildet sind, bzw. sich nicht mehr
ändern. (Bohl Seite 226)
3.3.2 Parabolisches Geschwindigkeitsprofil
Im kreisrunden Rohr werden die in der Achse strömenden Fluidteilchen durch Scherkräfte, die von
den Rohrwänden aus gehen, nach hinten gebremst. Dadurch
stellt sich ein Geschwindigkeitsprofil ein, das in der Mitte ein Maximum besitzt und an der Wand eine
l
Wandgeschwindigkeit = 0 aufweist.
wr
w
p1 p 2
2
r0 r 2
4 l
V
R2
wmax . 2 w
p1
p2
(Bohl ab Seite 151)
3.3.3 Turbulentes Geschwindigkeitsprofil
Anmerkung: Für die Berechnung von λturb ist je nachdem die Wandrauigkeit k verlangt.
pturb turb
3.3.4
2
w2
l
d
λturb ist der turbulente Widerstandsbeiwert (Bohl Seite 164 / 165)
Nicht-kreisrunde Strömungskanäle
14.05.2016
10 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
dh
4 A 4 Strömungsquerschnitt sfläche
U
benetzter Umfang
3.4
Reversible und irreversible Vorgänge, Zustandsgrösse Entropie
3.4.1
Reversible und irreversible Vorgänge
Ein reversibler Vorgang ist ein Vorgang, der sich vollständig rückführen lässt, ohne
dass in der Umgebung eine Veränderung zurückbleibt.
Ein irreversibler Vorgang lässt sich nur rückführen, wenn in der Umgebung bleibende
Veränderungen gemacht werden.
Für adiabate Systeme gelten:
In jedem irreversiblen Prozess:
dU p dV 0
Im Grenzfall des reversiblen Prozesses:
dU p dV 0
In adiabaten Systemen nicht möglich:
dU p dV 0
3.4.2
Gibb’sche Hauptgleichung:
Die Entropie S ist eine Zustandsgrösse, die Reversibilität bzw. Irreversibilität anzeigen kann.
dS
du p dv
T
dh v dp
ds
T
dq dwDiss
T
ds
J
kg K
du p dv dh v dp
T
T
s aus u oder h und den therm. ZGr. berechenbar
ds
ds
J
K
dU p dV dH V dp
T
T
s aus der Prozessführung berechenbar
u
v
h
p
1
p
1
v
f
T
v
s s ds du dv dh dp R ln R ln
T
T
T
T
2
T
v
u
v
h
p
(Letzte Formel gilt nur für f = konstant)
Für s = konstant wird mit der Isentropengleichung gerechnet.
Für s konstant wird mit der idealen Gasgleichung gerechnet.
3.4.3
Isentropenexponent
f 2
f
14.05.2016
Gasart
1-atomig
2-atomig
≥ 3-atomig
(nur falls fOsz.=0)
Freiheitsgrad f
Isentropenexponent κ
3
1.6666
5
1.40
6
1.33333
11 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
3.4.4 Isentropengleichung (Zusammenhang der ZGr bei konstanter Entropie )
Der nachfolgend abgeleitete Zusammenhang beschreibt das Verhalten der thermischen
Zustandsgrössen {p,v,T} und gilt nur, falls die Zustandsänderung die Randbedingung s = konstant
erfüllt.
p v p v
Druck:
p
p
v
v
T 1
T
spezifisches. Volumen:
v
v
p
p
Dichte:
v
v
p T 1
p
T
Temperatur:
T
T
p
p
1
1
1
1
1
v
v
T
T
1
1
1
1
1
Merke: Temperaturverhältnisse sind kleiner als Druckverhältnisse
3.4.5 Spezifische Arbeit bei konstanter Entropie
Geschlossenes System:
w p , geschl
1 v
R T
1 v
1
1
1 p
1 T
1 R T
1 R T
1 p
1 T
1
Offenes System:
w p ,offen
3.5
v
R T
1 v
1
1
p
T
1 R T
1 R T
1 p
1 T
1
Der 2. Hauptsatz
dφ ist die Wärme, die im Innern des Systems durch Reibungseffekte entstanden ist, also dem System
zugeführt wurde. Sie wird auch als Reibungswärme bezeichnet. Die Grösse dφ hat also die gleiche
Wirkung im System wie eine Wärmemenge dq, die von aussen über die Systemwand transportiert
wird.
du p dv
dh v dp dq d
T ds
es gilt dabei immer:
14.05.2016
d 0
aber
dq beliebig
12 / 16
J
dq ; d :
kg
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
3.6
Das T-S-Diagramm
Formel für das T-s-Diagramm:
T ds q
Der 3. Hauptsatz, Nernst’sches Wärmetheorem
3.7
Im 2. Hauptsatz interessieren vor allem die Entropieunterschiede zwischen 2 Zuständen interessieren
und der absolute Wert der Entropie eines Zustandes weniger interessiert. Erst wenn durch chemische
Reaktionen die Substanzen in einem System von einem Anfangszustand α in einen Endzustand ω
ihre Zusammensetzung ändern, muss man eine gemeinsame Entropieskala anwenden. Daraus
entstand der 3. Hauptsatz:
Die (absolute) Entropie eines homogenen festen Körpers, der sich in ungehemmtem
thermischen Gleichgewicht befindet, nähert sich dem Wert Null, wenn sich die
Temperatur dem absoluten Nullpunkt nähert.
3.8
lim sabs 0
T 0 K
Kreisprozesse
Ein geeignetes Medium durchläuft eine Serie von Zustandsänderungen, so dass schlussendlich
wieder der gleiche Zustand erreicht wird wie am Anfang.
Wärmekraft-Maschinen produzieren als Nutzen Wellenenergie. Dazu benötigt werden zwei
Wärmereservoire.
Kältemaschinen und Wärmepumpen produzieren ein Wärmeresevoir (bei Wärmepumpe
Nutzwärme, bei Kältemaschinen Nutzkälte). Sie benötigen mechanische Antriebsenergie und
ein zweites Wärmereservoir.
3.8.1
Kreisprozessanalyse
Zustandsänderungen in geeigneten Diagrammen einzeichnen
Involvierte Energiemengen (Arbeit und Wärme) identifizieren
Apparativer Aufbau studieren
Nutzen und Aufwand bestimmen
Wirkungsgrad berechnen
Wirkungsgrad :
abgeführte Arbeit
Nutzen
Aufwand zugeführte Energie
Wärmemengen können im T-s-Diagramm sichtbar gemacht werden
Arbeitsmengen können im p-v-Diagramm sichtbar gemacht werden
14.05.2016
13 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
Carnot-Prozess
Jouleprozess
Stirlingprozess
Isentrope Kompression
Isotherme Expansion
Isentrope Expansion
Isotherme Kompression
Isentrope Kompression
Isobare Wärmezufuhr
Isentrope Expansion
Isobare Wärmeabfuhr
Isochore Wärmezufuhr
Isotherme Expansion
Isochore Wärmeabfuhr
Isotherme Kompression
3.8.2
Wirkungsgrad Joule-Prozess
T4 T1
T3 T2
Joule Pr ozess 1
p
T
th 1 1 1 1
T2
p2
1
1
1
1
Druckverhältnis:
p 2 poben
p1 punten
opt. Wirkungsgrad:
optimale Temperatur:
T2,opt T1 T3
opt 1
T1
T3
Je grösser der Druckunterschied, desto besser der Wirkungsgrad
Der theoretische thermische Wirkungsgrad hängt nur von der 1. Kompression ab, und nicht
etwa von T3
Für gute Wirkungsgrade:
1-atomige Gase (jedoch in Praxis problematisch)
grosse Druckverluste
14.05.2016
14 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
3.9
Realer Kreisprozess am Beispiel Gasturbine
Bei realem Verdichter und Turbine gilt: d > 0 ds > 0
Die Entropie nimmt immer zu, auch bei Entspannung!
Verdichter: V , is
h2, is h1
his
hreal h2, real h1
Turbine: T , is
allgemein: V , is
h3 h 4 , real
allgemein: T , is
h3 h 4 , is
T2, is
T1
p
oben
punten
1
1
T2, is T1
T2, real T1
T3 T4 , real
T3 T4 , is
T3
T4, is
3.9.1 Totalenthalpie-Zustände im Gasturbinen-Prozess
Beim Begriff Totalenthalpie geht man von der Modellvorstellung aus, dass die in einem
Strömungszustand vorhandene kinetische Energie isentrop in thermische Energie umgewandelt wird,
indem die Strömungsgeschwindigkeit auf 0 reduziert wird. Damit kann sie auch in den relevanten
Diagrammen eingezeichnet werden.
h0 h
wV h20 h10
0
14.05.2016
w2
2
wT h30 h40
0
15 / 16
Version 1.0
Formelsammlung: Thermo- und Hydrodynamik
14.05.2016
16 / 16
Version 1.0