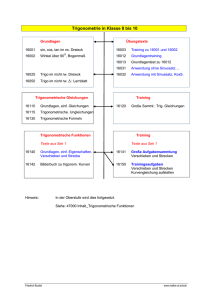
FFT–Algorithmus (fast fourier transform, Gauß 1805, Cooley

FFT–Algorithmus (fast fourier transform, Gauß 1805, Cooley-Tukey 1965)
Reeller Input yk k=0...7: 8 Funktionswerte
an den äquidistanten Stützstellen xk= k·2/8
(2-periodisch angenommen).
Beachte Reihenfolge der yk!
3
f ( x)  c0   (an cos(nx)  bn sin(nx))  c4 cos(4 x)
n 1
f ( xk )  yk
" f interpoliert ( xk , yk )"
Prof. Dr. Müller-Horsche
FH Augsburg
Ingenieurmathematik
Komplexer Output „Spektralwerte“ cn n=0...4:
Diese können wie angegeben in reelle a- und b-Werte
umgerechnet werden, mit denen dann die „trigonometrische
Interpolation“ der Funktionswerte (xk,yk) gelingt (s. Formel)
butterfly
y0
8·c0 immer reell, Mittelwert oder
„Gleichspannungsanteil“
y4
8·c1 a1 = 2·Re(c1) b1 = -2·Im(c1)
Grundwelle
y2
8·c2 a2 = 2·Re(c2) b2 = -2·Im(c2)
1. Oberwelle
y6
8·c3 a3 = 2·Re(c3) b3 = -2·Im(c3)
2. Oberwelle
y1
8·c4 immer reell
Oberwellenrest
y5
1 j
2
Zahl
Zahl
Zahl
Zahl
y3
y7
Erläuterung:
1  j
2
wird weitergeleitet
wird mit –1 multipliziert und weitergeleitet
wird mit j multipliziert und weitergeleitet
wird mit –j multipliziert und weitergeleitet
mit Inhalt des Rechtecks multiplizieren und
weiterleiten
alle von links in einen Kreis eingehenden Zahlen
werden addiert und ergeben den neuen Kreisinhalt
6
6
Prof. Dr. Müller-Horsche
FH Augsburg
Ingenieurmathematik
y6
y5
4
y
D( t )
0
y4
y7
y3
2
FFT–Algorithmus (Beispiel: Sägezahn)
y2
0 y0
0
y1
0.5
0
1
1.5
2
x t

 
2.5
3
3.5
4
x/3.998
y0
0
4
12
y4
4
-4
-4 + 4j
y2
2
y6
6
8
-4
8·c0 c0 = 3
24
4  2 2
 j 4 2 2

-4

1 
 8·c1 a1 =  1  2  = b1


8·c2 a2 = -1 b2 = 0
-4
4  2 2
 j 4  2 2

-4 - 4j
c0
 8·c a = 1  1 = -b
3
3
3
2
y1
y5
1
5
6
-4
12
-4
8·c4 c4 = 0
0
1 j
6
2
3
6
f ( t)
0
Fourier
Reihe
3
3
a1
-1,707 -1,621
b1
-1,707 -1,621
a2
-1
-0,811
b2
0
0
a3
-0,293 -0,180
b3
0,293
0,180
a4
0
0
b4
-
0
trigonometrische
Interpolation
4
y
y5
6
FFT
2
3
y7
3
0
-4
1  j
2
0
0
0
0
0.5
1
1.5
2
x t

 
2.5
3
3.5
4
x/3.998