Diskrete Fouriertransformation, FFT

Inhaltsverzeichnis
1
Inhaltsverzeichnis
Diskrete Fouriertransformation
Fast Fourier-Transform (FFT)
3
1 Diskrete Fouriertransformation
3
2 Anwendungen der diskreten Fouriertransformation
4
2.1
Fourierreihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
2.2
Trigonometrische Interpolation, Teil 1 . . . . . . . . . . . . . . . . . . .
5
2.3
Trigonometrische Interpolation, Teil 2 . . . . . . . . . . . . . . . . . . .
5
3 Fast Fourier-Transform (FFT)
10
3.1
Vorüberlegungen (FFT) . . . . . . . . . . . . . . . . . . . . . . . . . .
10
3.2
Algorithmus (FFT) . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
3.3
JAVA Quelltext für FFT . . . . . . . . . . . . . . . . . . . . . . . . . .
13
2
Inhaltsverzeichnis
3
Diskrete Fouriertransformation
Fast Fourier-Transform (FFT)
Jan Henrik Sylvester
1
Diskrete Fouriertransformation
Definition 1.1 Zu einem gegebenen Datensatz von N komplexen Zahlen f0 , f1 , ..., fN −1
bezeichnet der Datensatz d0 , d1 , ..., dN −1 komplexer Zahlen definiert durch
N −1
1 X −ijk2π/N
fi e
,
dk =
N j=0
k = 0, 1, ..., N − 1
(i =
√
−1)
(1)
die diskrete Fouriertransformierte von f0 , ..., fN −1 . Es wird auch folgende Notation verwendet,
F[f0 , ..., fN −1 ] := [d0 , ..., dN −1 ].
(2)
Mit der Matrix
V := (ω kj )k,j=0..N −1

1
1


= 1
 ..
.
1
ω
ω2
..
.
1
ω2
ω4
..
.
1 ω N −1 ω 2(N −1)
ergibt sich die Fouriertransformierte

d0
 ..
 .

...
1
. . . ω N −1 

. . . ω 2(N −1) 
 ∈ CN ×N , ω := ei2π/N (3)
.. 
...
. 
(N −1)2
... ω
durch Multiplikation:



f0
1  . 

 = V  .. 
N
dN −1
fN −1
(4)
4
Diskrete Fouriertransformation
Fast Fourier-Transform (FFT)
In der Matrix (3) sind jeweils der k-te Zeilen- und Spaltenvektor gleich. Da die Zeilenvektoren eine orthonomarle Basis bilden, ist da Skalarprodukt der Zeilen- und Spaltenvektoren mit dem gleichen Index 1, ansonsten 0. Deshalb gilt
1 −1
V
= V.
N
(5)
Man erhält das folgende Korollar.
Korollar 1.2 Jeder Datensatz f0 , ..., fN −1 komplexer Zahlen lässt sich also aus seiner
diskreten Fouriertransformierten F[f0 , ..., fN −1 ] = [d0 , ..., dN −1 ] mittels
fj =
N
−1
X
dk eijk2π/N ,
j = 0, 1, ..., N − 1,
(6)
k=0
zurückgewinnnen. Es wird auch die folgende Notation verwendet,
F −1 [d0 , ..., dN −1 ] = [f0 , ..., fN −1 ].
2
2.1
(7)
Anwendungen der diskreten Fouriertransformation
Fourierreihen
Im folgenden werden sowohl reelle, als auch komplexe Darstellungen verwendet. Aus
der Eulerschen Formel folgt:
e±ik2πx/L = cos k
2πx 2πx ± i sin k
,
L
L
i=
√
−1
(k ∈ Z).
(8)
Jede Riemann-integrierbare Funktion f : [0, L] → R mit f (0) = f (L) lässt sich in eine
Fourierreihe entwickeln,
∞
a0 X h
2πx 2πx i
f (x) =
+
ak cos k
+ bk sin k
,
2
L
L
k=1
(9)
mit den reellen Fourierkoeffizienten
2
ak =
L
Z
0
L
2πy f (y) cos k
dy,
L
2
bk =
L
Z
L
f (y) sin k
0
2πy dy
L
(10)
oder als komplexe Fourierentwicklung
f (x) =
∞
X
k=−∞
ck eik2πx/L
(11)
2 Anwendungen der diskreten Fouriertransformation
5
mit den komplexen Fourierkoeffizienten
Z
1 L
ck =
f (y)e−ik2πy/L dy,
L 0
k ∈ Z.
(12)
Es besteht der Zusammenhang
ak − ibk
,
2
ak = ck + c−k ,
ck =
2.2
ak + ibk
,
2
bk = i(c−k − ck ).
c−k =
(13)
(14)
Trigonometrische Interpolation, Teil 1
Der abgebrochene Fourierreihe eignet sich zur Interpolation periodischer Funktionen
mit der Periode L auf dem Interval [0, L] mit L > 0. Dafür werden trigonometrische
Polynome der folgenden Form herangezogen,
p(x) =
N
−1
X
dk eik2πx/L ,
x ∈ R.
(15)
k=0
Theorem 2.1 Zu äquidistanten Stützstellen xj = jL/N ∈ [0, L] und beliebigen Stützwerten fj ∈ C für j = 0, 1, ..., N − 1 mit N ∈ N besitzt das trigonometrische Polynom
p aus (15) die Interpolationseigenschaft
j = 0, 1, ..., N − 1,
p(xj ) = fj ,
(16)
genau dann, wenn (F )[f0 , ..., fN −1 ] = [d0 , ..., dN −1 ] erfüllt ist.
Beweis: Die Interpolationsbedingungen (16) ausgeschrieben bedeuten
fj =
N
−1
X
dk eijk2π/N ,
j = 0, 1, ..., N − 1,
(17)
k=0
was mit der Fourierrücktransformation (6) übereinstimmt. Die Aussage folgt unmittelbar.
2
Diese trigonometrischen Polynome oszillieren stark und konvergieren nicht (Abbildung
2.1), da noch Terme bis k = N − 1 verwendet werden.
2.3
Trigonometrische Interpolation, Teil 2
Bessere Interpolationseigenschaften haben folgende trigonometrische Polynome, bei denen weniger stark oszillierende Terme mit unterschiedlichen Vorzeichen verwendet werden,
N/2−1
r(x) =
X
k=−N/2
dk eik2πx/L ,
N gerade.
(18)
6
Diskrete Fouriertransformation
Fast Fourier-Transform (FFT)
Abbildung 2.1: Dreieck (f (x) = 0.5−|x−[x]−0.5|) mit 8 und 32 Interpolationspunkten
(nach (15)).
Theorem 2.2 Zu äquidistanten Stützstellen xj = jL/N ∈ [0, L] und Stützwerten
fj ∈ C für j = 0, 1, ..., N − 1 mit N ∈ N gilt für die Funktion r aus (18) die Interpolationseigenschaft
j = 0, ..., N − 1
r(xj ) = fj ,
(19)
genau dann, wenn
F[(−1)0 f0 , (−1)1 f1 , ..., (−1)N −1 fN −1 ] = [d−N/2 , ..., dN/2−1 ]
(20)
erfüllt ist.
Beweis: Eine Umindizierung führt auf
=:p(x)
r(x) =
N
−1
X
k=0
dk−N/2 ei(k−N/2)2πx/L =
z
N
−1
X
}|
{
dk−N/2 eik2πx/L e−iN πx/L
(21)
k=0
mit dem trigonometrischen Polynom der Form (15). Das Theorem folgt unmittelbar
mit e−iN πxj /L = e−ijπ = (−1)j .
2
2 Anwendungen der diskreten Fouriertransformation
7
Abbildung 2.2: Dreieck (f (x) = 0.5−|x−[x]−0.5|) mit 8 und 32 Interpolationspunkten.
(nach (18))
Diese Polynome haben bessere Interpolationseigenschaften. Sie oszillieren schwächer
und konvergieren für stetige Funktionen (Abbildung 2.2). Lediglich an Unstetigkeitsstellen ist der Fehler nur von der Sprunghöhe abhängig, nicht aber von der Anzahl der
Stützstellen; dieses nennt sich Gibbisches Phänomen (Abbildung 2.3).
Die trigonometrische Interpolation eignet sich zur Datenglättung (Abbildung 2.4), wenn
hochfrequente Störungen auf ein niederfrequentes Signal aufmoduliert sind, sofern nur
Therme mit niedrigerer Oszillation als die Störung verwendet werden, dh. N nicht zu
hoch gewählt wird.
Zur Interpolation mit reellen Stützstellen können reelle trigometrische Polynome der
folgenden Form herangezogen werden,
T (x) = A0 + 2
N/2−1 X
k=1
k2πx k2πx N πx Ak cos
+ Bk sin
+ AN/2 cos
L
L
L
(22)
mit geradem N , wobei für die Koeffizienten gilt
N −1
1 X
jk2π Ak =
fj cos
∈ R,
N j=0
N
N −1
1 X
jk2π Bk =
fj sin
∈ R,
N j=0
N
(23)
k = 0, 1, ..., N/2.
(24)
8
Diskrete Fouriertransformation
Fast Fourier-Transform (FFT)
Abbildung 2.3: Sägezahn (f (x) = x − [x]) und Rechteck mit 32 Interpolationspunkten.
Lemma 2.1 Zwischen den Koeffizienten Ak , Bk , k = 0, 1, ..., N − 1 in (23) und der
diskreten Fouriertransformierten aus (20) bestehen die Zusammenhänge
d0 = A0 ,
dk = Ak − iBk ,
d−N/2 = AN/2 ,
d−k = Ak + iBk ,
k = 1, 2, ..., N/2 − 1
(25)
(26)
Beweis: Entsprechend (20) gilt
dk−N/2 =
N −1
1 X
(−1)j fj e−ijk2π/N ,
N j=0
k = 0, 1, ..., N − 1,
(27)
beziehungsweise
N −1
1 X
dk =
(−1)j fj e−ijk2π/N e|−ijπ
{z }
N j=0
j
(28)
=(−1)
=
N −1
1 X h
jk2πx jk2πx i
fj cos
− i sin
,
N j=0
N
N
k = −N/2, ..., N/2 − 1,
woraus die angegebenen Identitäten unmittelbar folgen.
(29)
2
2 Anwendungen der diskreten Fouriertransformation
9
Abbildung 2.4: Gestörtes Signal und Fourier-Interpolation mit 8 Interpolationspunkten.
Theorem 2.3 Für die trigonometrische Funktion r aus (18) und T aus (22) gilt <r(x) =
T (x) sowie T (xj ) = fj für j = 0, 1, ..., N − 1 (< bedeutet Realanteil).
Beweis: Mit der trigonometrischen Funktion r aus (18) gilt
r(x) =d0 +
N/2−1 X
dk eik2πx/L + d−k e−ik2πx/L + d−N/2 e−iN πx/L
k=1
(*)
=A0 +
N/2−1 X
ik2πx/L
(Ak − iBk )e
−ik2πx/L
+ (Ak + iBk )e
+ AN/2 e−iN πx/L
(30)
k=1
=A0 + 2
N/2−1 X
k=1
Ak cos
k2πx + Bk sin k2πxL + AN/2 e−iN πx/L
L
wobei in (*) noch das vorangegangene Lemma herangezogen wurde. Aus dieser Darstellung für r ergeben sich unmittelbar die beiden Aussagen des Theorems.
2
10
3
3.1
Diskrete Fouriertransformation
Fast Fourier-Transform (FFT)
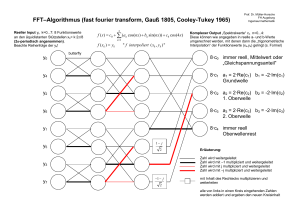
Fast Fourier-Transform (FFT)
Vorüberlegungen (FFT)
Eine Berechnung der Fouriertransformation mittels einer Matrix-Vektor-Multiplikation
hat einen hohen Rechenaufwand von N 2 komplexen Multiplikationen. Dagegen benötigt
die nun vorgestellte schnelle Fouriertransformation lediglich O(N log2 (N )) komplexe
Multiplikationen.
Theorem 3.1 Aus der diskreten Fouriertransformation der beiden (komplexen) Datensätze g0 , g1 , ..., gM −1 und gM , gM +1 , ..., g2M −1 der Längen M lässt sich die Fouriertransformierte des Datensatzes g0 , gM , g1 , gM +1 , ..., gM −1 , g2M −1 der Länge 2M folgendermaßen bestimmen:
1
−ikπ/M
Fk [g0 , g1 , ..., gM −1 ] + e
F[gM , gM +1 , ..., g2M −1 ]
2
= Fk [g0 , gM , g1 , gM +1 , ..., gM −1 , g2M −1 ]
1
−ikπ/M
Fk [g0 , g1 , ..., gM −1 ] − e
F[gM , gM +1 , ..., g2M −1 ]
2
= FM +k [g0 , gM , g1 , gM +1 , ..., gM −1 , g2M −1 ]
k = 0, 1, ..., M − 1
(31)
(32)
(33)
Hierbei bezeichnen Fk bezeihungsweise FM +k die k-te beziehungsweise (M + k)-te Komponente von F.
Beweis: Für k = 0, 1, ..., M − 1 gilt
Fk [g0 , gM , g1 , gM +1 , ..., gM −1 , g2M −1 ]
M
−1
M
−1
X
X
1
−i2jk2π/2M
−i(2j+1)k2π/2M
=
gj e
+
gM +j e
2M j=0
j=0
M
−1
M
−1
X
X
1
−ijk2π/M
−ikπ/M
−ijk2π/M
=
gj e
+e
gM +j e
.
2M j=0
j=0
(34)
Die zweite Gleichung im Theorem erhält man völlig analog, wobei noch
e−ij(k+M )2π/2M = e−ijπ e−ijk2π/2M = (−1)j e−ijk2π/2M
berücksichtigt wird.
(35)
2
Damit können nun Datensätze der Länge N = 2q mit q ∈ N rekursiv oder iterativ
transformiert werden, wobei letzteres speichersparender ist und im Folgenden behandelt
3 Fast Fourier-Transform (FFT)
11
wird. Schema beispielhaft für r = 3:
Stufe 0
Stufe 1
Stufe 2
Stufe 3
f0
f4
f2
f6
f1
f5
f3
f7
k
k
k
k
k
k
k
k
F[f0 ] F[f4 ] F[f2 ] F[f6 ] F[f1 ] F[f5 ] F[f3 ] F[f7 ]
&
.
&
.
&
.
&
.
F[f0 , f4 ]
F[f2 , f6 ]
F[f1 , f5 ]
F[f3 , f7 ]
&
.
&
.
F[f0 , f2 , f4 , f6 ]
F[f1 , f3 , f5 , f7 ]
&
.
F[f0 , f1 , f2 , f3 , f4 , f5 , f6 , f7 ]
(36)
Um die anfängliche Reihenfolge zu erhalten, kann die Bit-Umkehr verwendet werden.
Position
Index von f
Dezimal , Binär Binär revers , Dezimal
0
000
000
0
100
4
1
001
010
2
2
010
Für das Beispiel erhält man:
110
6
3
011
4
100
001
1
101
5
5
101
011
3
6
110
111
7
7
111
Pq−1 l
Definition 3.1 Für q ∈ N0 sei k = l=0
bl 2 die eindeutige Binärdarstellung einer
q
Zahl k ∈ Mq = {0, ..., 2 − 1} mit Binärziffern (Bits) bl ∈ {0, 1}. Die durch
σq : Mq → Mq ,
q−1
X
bl 2l 7→
q−1
X
l=0
bq−1−l 2l
(37)
l=0
definierte Abbildung bezeichnet man als Bit-Umkehr.
Bemerkung 3.2 Die Bit-Umkehr σq : Mq → Mq ist bijektiv mit σq−1 = σq . Um sie
effizient zu implementieren sollte noch Folgendes beachtet werden, wobei die Beweise
elementar sind:
σq (2r + k) =σq (k) + 2q−1−r ,
σr (k) =σr+1 (2k),
r
2 + σr (k) =σr+1 (2k + 1),
3.2
k = 0, ..., 2r − 1; r = 0, ..., q − 1
r = 0, 1, ...; k ∈ Mr
r = 0, 1, ...; k ∈ Mr
(38)
(39)
(40)
Algorithmus (FFT)
Ausgehend von Zahlen d[0,j] = gj ∈ C, j = 0, ..., 2q − 1 bestimme man für Stufen
r = 1, 2, ..., q in der r-ten Stufe insgesamt 2q−r Vektoren der Länge 2r
d[r,0] , d[r,1] , ..., d[r,2
q−r −1]
∈ C2
r
(41)
12
Diskrete Fouriertransformation
Fast Fourier-Transform (FFT)
aus den Datensätzen der jeweils vorhergehenden Stufe r − 1 gemäß der folgenden Vorschrift:
[r+1,j]
dk
:=
1 [r,2j]
1 [r,2j]
[r,2j+1] [r+1,j]
[r,2j+1] dk + θ(r)k dk
, d2r +k := dk − θ(r)k dk
,
2
2
k = 0, ..., 2r − 1, j = 0, ..., 2q−r−1 − 1, r = 0, ..., q − 1
(42)
r
mit den Zahlen θ(r) := e−iπ/2 , r = 0, ..., q − 1. Der Algorithmus wird schematisch
dargestellt:
Stufe 0
Stufe 1
Stufe 2
..
.
g0
g1
g2
g3
k
k
k
k
[0,0]
[0,1]
[0,2]
[0,3]
d
d
d
d
&
.
&
.
[1,0]
[1,1]
d
d
&
.
[2,0]
d
&
..
.
&
Stufe q − 1
Stufe q
...
...
...
...
...
...
...
g2q −4
g2q −3
g2q −2
g2q −1
k
k
k
k
[0,2q −4]
[0,2q −3]
[0,2q −2]
[0,2q −1]
d
d
d
d
&
.
&
.
[1,2q−1 −2]
[1,2q−1 −1]
d
d
&
.
[2,2q−2 −1]
d
.
.·
·
.
d[q−1,0] d[q−1,1]
& .
d[q,0]
(43)
Theorem 3.2 Es gilt
d[r,j] = F[gj2r +σr (0) , gj2r +σr (1) , ..., gj2r +σr (2r −1) ]
j = 0, 1, ..., 2q−r − 1, r = 0, 1, ..., q.
(44)
Beweis: Es wird vollständige Induktion über r angewandt. Die Aussage (44) ist sicher
richtig für r = 0, und im Folgenden sei (44) richtig für ein 0 ≤ r ≤ q−1. Dann berechnet
man unter Berücksichtigung von 2j2r = j2r+1 Folgendes,
[r+1,j]
dk
1
= Fk [g2j2r +σr (0) , ..., g2j2r +σr (2r −1) ] + θ(r)k Fk [g(2j+1)2r +σr (0) , ..., g(2j+1)2r +σr (2r −1) ]
2
=Fk [gs0 , ..., gs2r+1 −1 ]
(45)
mit
σr+1 (2k)
z }| {
s2k :=j2
+ σr (k) ,
s2k+1 :=j2r+1 + 2r + σr (k),
| {z }
r+1
σr+1 (2k+1)
k = 0, 1, ..., 2r − 1,
(46)
3 Fast Fourier-Transform (FFT)
13
unter Berücksichtigung der Bemerkungen zur Bit-Umkehr (39) und (40). Die angege[r+1,j]
bene Darstellung für d2r +k ergibt sich durch die gleiche Rechnung, mit θ(r)k ersetzt
durch −θ(r)k . Dies komplettiert den Beweis des Theorems.
2
Korollar 3.3 Der FFT-Algorithmus liefert
d[q,0] = F[gσq (0) , ..., gσq (2q −1) ].
(47)
Die Setzung gk = fσq (k) , k = 0, 1, ..., 2q − 1, führt somit auf d[q,0] = F[f0 , ..., f2q −1 ].
3.3
JAVA Quelltext für FFT
public static class C implements Cloneable {
public double re; public double im;
public C(double re, double im) {this.re = re; this.im = im;}
public C() {re = 0; im = 0;}
public Object clone() {return new C(re, im);}
public void copyTo(C z) {z.re = re; z.im = im;}
public void conj0() {im = -im;}
public void neg0() {re = -re; im = -im;}
public void add0(C z) {re += z.re; im += z.im;}
public void sub0(C z) {re -= z.re; im -= z.im;}
public void mult0(C z) {double tre=re*z.re-im*z.im; im=re*z.im+im*z.re;
re=tre;}
public void div0(double z) {re /= z; im /= z;}
}
/**
* does Fast Fourier-Transform
* @param f values
* @return Fourier-Transform
*/
public static C[] fft(C f[]) {
int M0, q; for(q = 0, M0 = 1; M0 < f.length; q++, M0 <<= 1); // q=lb(M0)
if(M0 != f.length) throw new UnsupportedOperationException(
"Array length must be 2^n for Fast Fourier-Transform.");
C d[] = new C[M0]; // Fourier coefficients
for(int k = 0; k < M0; k++) { // initialisation loop
int k0 = 0; // for bit reversal
for(int m = 1, m0 = 1 << (q - 1); m <= k; m <<= 1, m0 >>= 1)
if((k & m) != 0) k0 |= m0; // do bit reversal via masks
d[k] = (C)f[k0].clone(); // initialize
}
for(int r = 0, M = 1; r < q; r++, M <<= 1) {
C phi = new C(); double PI_M = Math.PI / (double)M;
14
Diskrete Fouriertransformation
Fast Fourier-Transform (FFT)
C phi1 = new C(Math.cos(PI_M), -Math.sin(PI_M)); C x = new C();
for(int k = 0; k < M; k++) {
if(k > 1) phi.mult0(phi1); // phi=e^(-i*k*PI/M)
else if(k == 1) phi1.copyTo(phi);
else {phi.re = 1.0; phi.im = 0.0;}
for(int j = 0, j0 = 1 << (q - r - 1); j < j0; j++) {
int j2 = 2 * j * M + k, j1 = j2 + M; // work on these 2
d[j1].copyTo(x); x.mult0(phi); // *phi to temp
d[j2].copyTo(d[j1]); d[j1].sub0(x); d[j1].div0(2.0); // diff
d[j2].add0(x); d[j2].div0(2.0); //sum
}
}
}
return d;
}
Bemerkung 3.4 Kommentare an Jan Henrik Sylvester <[email protected]>