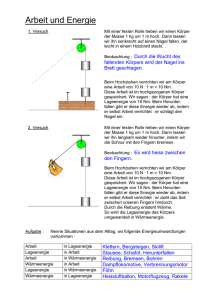
Karteikarten - Energieerhaltung - Schulen
Werbung
M Energieerhaltung Begründen EE/1 Lösung: Wo bleibt die Energie EE/1 Die Kohle verbrennt nicht heißer. Sie brennt auch nicht länger. Aber die Verbrennungsprodukte besitzen bei ihrer Entstehung eine um 10m erhöhte Lage. Sie weisen daher eine potenzielle Energie auf, die um die selbe Energiedifferenz erhöht ist, wie die Lageenergie der Kohle Wo bleibt die Energie Trägt man einen Eimer mit Kohle (5kg) aus dem Keller in den dritten Stock (Höhenunterschied rund 10m) erhöht sich die potenzielle Energie (=Lageenergie) der Kohle um etwa 500 J (Gewichtskraft 50 N• Höhenunterschied 10m) Was geschieht nun mit dieser zusätzlichen potenziellen Energie, wenn die Kohle im Ofen verbrannt wird? Verbrennt die Kohle dann heißer oder brennt sie länger? M Energieerhaltung Begründen EE/2 Die schwebende Rakete – wo bleibt die Energie? Eine Rakete ist senkrecht aufgestellt. Die Schubkraft ihres Triebwerks kann durch Regelung der Treibstoffzufuhr verändert werden. Die Schubkraft wird nun so eingestellt, dass sie die Gewichtskraft der Rakete ausgleicht. Die Rakete schwebt. Der in den Triebwerken verbrannte Treibstoff erzeugt eine Schubkraft. Aber an der Rakete wird keine Arbeit verrichtet, denn es wird ja kein Weg zurückgelegt Wohin „verschwindet“ die chemische Energie des Treibstoffes Erkläre diesen scheinbaren Widerspruch Lösung: Die schwebende Rakete Die chemische Energie wird verwandelt in Wärmeenergie und kinetische Energie der verbrannten Gasmassen EE/2 L Energieerhaltung Berechnen EE/3 Lösung: Freie Fall aus 30m EE/3 E pot E kin Freie Fall aus 30m Ein Stein fällt aus einer Höhe von 30m frei herab. Mit welcher Geschwindigkeit (in km/h) trifft er auf dem Boden auf, wenn Reibung (Luftwiderstand) vernachlässigt wird? Energieerhaltung Berechnen 1 mv 2 2 m km 87 s h Der Stein trifft mit 87 km/h auf. v 2gh 2.9,81.30 24 Lösung ohne Energieerhaltungssatz 1 s gt 2 2 2s 2s t v g .t v g . 2 gs g g Verwende zur Lösung den Energieerhaltungssatz! M mgh EE/4 Lösung: Der hüpfende Tischtennisball EE/4 Energie kann die Form wandeln, ohne den Besitzer zu wechseln. Der hüpfende Tischtennisball Ein Tischtennisball wird auf eine harte Tischplatte fallen gelassen. Beschreibe die Energieumwandlungen. Warum nimmt die Sprunghöhe ständig ab? Der Ball wird angehoben: Er erhält Lageenergie. Der Ball fällt: Die anfangs vorhandene Lageenergie verwandelt sich mit schwindender Höhe zunehmend in Bewegungsenergie. Der Ball stößt auf: Die gesamte Bewegungsenergie verwandelt sich beim Aufprall in Spannenergie, der Ball wird leicht zusammengedrückt. Der Ball stößt ab: Die Spannenergie verwandelt sich beim zurückprallen wieder in Bewegungsenergie, der Ball entspannt sich Der Ball steigt: Mit zunehmender Höhe nimmt die Bewegungsenergie ab, dabei erhöht sich die Lageenergie um am oberen Umkehrpunkt ihr Maximum zu erreichen. Nun beginnt das Spiel von vorne. Irgendwann kommt der Ball jedoch zum Stillstand. Das liegt daran, dass er durch Luftreibung, Reibung beim verformen und durch Schall Energie verliert L Energieerhaltung Berechnen EE/5 Lösung: Auto gegen Mauer geg: v = 108 Auto gegen Mauer Ein Auto prallt mit 108 km/h gegen eine feste Mauer. Aus welcher Höhe müsste es frei herabfallen, um die gleiche zerstörende Energie zu bekommen ? L Energieerhaltung Berechnen Rollende Kugel Eine Kugel rollt reibungsfrei aus der Höhe h = 2 m herab. km Welche Geschwindigkeit erreicht sie (in )? h EE/6 EE/5 km 108 m m 30 h 3,6 s s ges: h Ekin = Epot mv 2 m.g.h /m 2 v2 g.h 2 v2 30 2 h m 45,87 m 2g 2.9,81 Das Auto müsste aus über 45 m Höhe herabfallen Lösung: Rollende Kugel EE/6 Wenn die Kugel reibungsfrei aus dieser Höhe hinabrollt, wandelt sie ihre gesamte potenzielle Energie in kinetische Energie um Epot = Ekin mv 2 m.g.h /:m 2 v2 g.h 2 m m km v 2.g.h 2.9,81.2 6,26 22,6 s s h Bemerkung: Die gleiche Formel v 2gh erhält man, wenn man die Aufgabe über den freien Fall löst. Die Kugel hat also für das Herabrollen und den freien Fall aus 2 m Höhe die gleichen Geschwindigkeiten.