Kreher WS1819 Klausur aus Gedächtnis

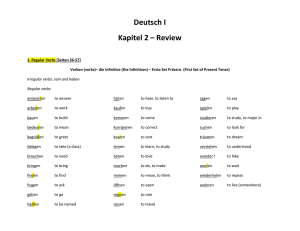
Stochastik II
Dörte Kreher, 18.02.2019, Gedächtnisprotokoll
Aufgabe 1
Let X ∈ L2 (Ω, F, P) and let G ⊂ F be a sub-σ-algebra of F.
a) We define the conditional variance V ar(X|G) := E((X − E(X|G))2 |G). Show that
V ar(x) = E(V ar(X|G)) + V ar(E(X|G)).
b) Let Y be another random variable on (Ω, F, P) and suppose that E(X 2 |Y ) = Y 2
a.s. and E(X|Y ) = Y a.s. Show that X = Y a.s.
Aufgabe 2
Let (Xn )n∈N be a sequence of i.i.d. random variables on a probability space (Ω, F, P)
1
such that P(Xn = 1) = P(Xn = −1) = . We define the filtration F0 := {∅, Ω},
P 2
Fn := σ(X1 , .., Xn ), n ∈ N, an set Sn := nk=1 Xk for all n ∈ N with S0 := 0. For c ∈ Z
we define the first hitting time τc := inf{n ∈ N0 : Sn = c}. Let a, b ∈ N and define
τ := τa ∧ τ−b .
a) Apply the stopping theorem so (Sn ) and compute P(τa < τ−b ) as a function of a, b.
b) Prove that Mn := Sn2 − n, n ∈ N0 , is a martingale with respect to (Fn )n∈N0 .
c) Apply the stopping theorem to (Mn ) and compute E(τ ) as a function of a, b.
Aufgabe 3
P
P
Let ϕ : N0 −→ R+ with n∈N ϕ(n) < ∞, and let φ(n) := nk=1 ϕ(k) and
Mn = ϕ(Mn )(Mn − Sn ) + φ(M –n).
a) Show that Mn is a martingale.
b) Does Mn converge and what is the limit? Is it uniformly integrable?
Aufgabe 4
Ms. Daisy has two suitors: Mr. Hampshire and Mr. Smith. Each month she changes the
relations to the suitors. If she is engaged to one of them at the beginning of a month,
there are now three possibilites for this month: She is either still engaged to this one,
or married to him, or engaged to his rival (with prabability 0.4, 0.3, 0.3). Assume that
marriage is permanently.
1
a) Write this as a 4-state Markov chain. Which states are transient and which recurrent?
b) Assume that Ms. Daisy ist engaged to Mr. Smith. What is the probability that she
marries him?
c) Assume that Ms. Daisy is not married. What ist the expected number of months
until marriage?
Aufgabe 5
Assume two urns. At the beginning, there are N black balls (no white balls) in the first
urn and N white balls (no black balls) in the second urn. At each time, there are two
balls (one of urn 1 and the other of urn 2) randomly choosen and exchanged. Denote by
Xn the number of black balls in urn 1.
a) Find the transition probabilities.
b) ...
Aufgabe 6
et be two independent Brownian motions. Define
a) Let Bt and B
Wt =
e
Bt + B
√ t
2
Show that Wt is a Brownian motion.
b) Let Sk be a simple random walk. Show that
"
#
1
E √
max Sk = E sup Bt
n 0≤k≤n
t∈[0,1]
lim
n−→∞
2