Lineare Gleichungssysteme und Matrizen
Lineare Algebra I
Volkmar Welker
Fachbereich Mathematik und Informatik
Philipps-Universität Marburg
WS 2023/24
Marburg 22. November 2023
1 / 37
Lineare Gleichungssysteme und Matrizen
Lineare Algebra I
3. Lineare Gleichungssysteme
und Matrizen
2 / 37
Lineare Gleichungssysteme und Matrizen
Problemstellungen aus Kapitel 3:
(2, 1, 0), (0, 1, 1), (0, 0, 1) ∈ R3 .
Sind diese 3 Vektoren linear unabhängig?
→ Lösungen der Gleichung
λ1 (3, 1, 0) + λ2 (0, 1, 1) + λ3 (0, 0, 1) = (0, 0, 0)
⇔
2λ1 + 0λ2 + 0λ3 = 0
1λ1 + 1λ2 + 0λ3 = 0
0λ1 + 1λ2 + 1λ3 = 0.
Im Folgenden: systematisches Lösen solcher Gleichungen
3 / 37
Lineare Gleichungssysteme und Matrizen
Denition (lineares Gleichungssystem)
Ein lineares Gleichungssystem mit n Gleichungen und m
Unbestimmten x1 , . . . , xm über dem Körper K ist gegeben durch
a11 x1 + . . . + a1m xm = b1
..
.
an1 x1 + . . . + anm xm = bn
für aij ∈ K, 1 6 i 6 n, 1 6 j 6 m und bi ∈ K, 1 6 i 6 n.
Gilt b1 = . . . = bn = 0K , so heiÿt das Gleichungssystem homogen ,
andernfalls inhomogen .
Die aij heiÿen Koezienten des Systems.
4 / 37
Lineare Gleichungssysteme und Matrizen
Besseren Darstellung eines linearen Gleichungssystems:
Denition (Matrix)
Eine Matrix mit n Zeilen und m Spalten über dem Körper K ist ein
Schema
a11 . . . a1m
..
..
A= .
.
an1 . . . anm
mit aij ∈ K, 1 6 i 6 n, 1 6 j 6 m. Wir schreiben auch
A = (aij )16i6n,16j6m .
5 / 37
Lineare Gleichungssysteme und Matrizen
Denition (Zeilen/Spaltenvektor)
Für b1 , . . . , bn ∈ K heiÿt
b1
..
.
bn
heiÿt Spaltenvektor und
(b1 , . . . , bn )
heiÿt Zeilenvektor .
6 / 37
Lineare Gleichungssysteme und Matrizen
Bemerkung
Bisher: Kn als Menge von Zeilenvektoren (a1 , . . . , an )
Ab jetzt: Kn je nach Kontext als Vektorraum von Zeilen- oder
Spaltenvektoren
Denition
Für die Matrix A = (aij )1616n,16j6m heiÿt der Vektor
a1j
..
.
anj
der j -te Spaltenvektor von A und
(ai 1 , . . . , aim )
der i -te Zeilenvektor von A.
7 / 37
Lineare Gleichungssysteme und Matrizen
Beispiel
2 0 0
1 1 0
0 1 1
ist Matrix mit Einträgen in R
(1, 1, 0) ist der zweite Zeilenvektor
0
1
ist der zweite Spaltenvektor.
1
8 / 37
Lineare Gleichungssysteme und Matrizen
Denition
Für ein lineares Gleichungssystem
a11 x1 + . . . + a1m xm = b1
..
.
an1 x1 + . . . + anm xm = bn
heiÿt
a11 . . . a1m
..
..
.
.
an1 . . . anm
die Koezientenmatrix und wir schreiben
b1
..
.
bn
als Spaltenvektor.
9 / 37
Lineare Gleichungssysteme und Matrizen
Denition (Matrix-Vektor Multiplikation)
Wir schreiben Kn×m für die Menge aller n × m Matrizen
aij 16i6n,16j6m über K. Wir denieren die Multiplikation
Kn×m × Km
→
v1
·:
(aij )1616n,16j6m , ... 7→
|
{z
} vn
| {z }
=A
=v
Kn
A·v =Av :=
a11 v1 + . . . + a1m vm
..
.
an1 v1 + . . . + anm vm
10 / 37
Lineare Gleichungssysteme und Matrizen
Beispiel
1
2 0 1
2 · 1 + 0 · (−2) + 1 · 5
7
−2 =
=
1 1 0
1 · 1 + 1 · (−2) + 0 · 5
−1
5
2 1 2·1−1·1
1
1 2 1 = 1 · 1 − 1 · 2 = −1
−1
1 1
1 · 1 + 1 · (−1)
0
11 / 37
Lineare Gleichungssysteme und Matrizen
Bemerkung
Sei A die Matrix des linearen Gleichungssystems
a11 x1 + · · · + a1m xm = b1
..
.
(∗)
an1 x1 + · · · + anm xm = bn
und b =
b1
..
.
bn
!
v1 . Dann gilt: v = ...
ist Lösung von (∗) ⇔
vm
a11 v1 + · · · + a1m vm
..
b = Av =
.
.
an1 v1 + · · · + anm vm
12 / 37
Lineare Gleichungssysteme und Matrizen
Bemerkung (Sprechweise)
A = aij
16i6n,16j6m
und b =
b1
..
.
!
bn
Mit dem linearen Gleichungssystem
a11 x1 + · · · + a1m xm = b1
..
.
(∗)
an1 x1 + · · · + anm xm = bn ,
heiÿt auch
Ax = b
x1 für x = ...
lineares Gleichungssystem und
v xm
1
.. ∈ Km Av = b
LA,b =
.
vm
heiÿt Lösungsmenge des linearen Gleichungssystems
13 / 37
Lineare Gleichungssysteme und Matrizen
Satz 4.1
A ∈ Kn×m , b ∈ Kn .
Dann gilt
(i) Für b =
0K
..
.
!
= 0Kn ist LA,b ein Untervektorraum des Km .
0K
(ii) Für b 6=
0K
..
.
!
= 0Kn gilt entweder
0K
LA,b = ∅
oder
LA,b = v + LA,0Kn = {v + w | w ∈ LA,0Kn }
für ein v ∈ LA,b .
14 / 37
Lineare Gleichungssysteme und Matrizen
Zum Beweis das Satzes benötigen wir folgendes Lemma:
Lemma 4.2
A ∈ Kn×m , v , w ∈ Km , λ, µ ∈ K.
Dann gilt
A(λv + µw ) = λ(Av ) + µ(Aw ).
15 / 37
Lineare Gleichungssysteme und Matrizen
Beweis.
v1
A = (aij )16i6n,16j6m , v =
.
.
.
w1
!
,
w=
vm
Dann ist
.
.
.
!
.
wm
λv1 + µw1
.
.
.
λv + µw =
λvm + µwm
und
A λv + µw
a11 (λv1 + µw1 ) + . . . + a1m (λvm + µwm )
.
.
.
=
an1 (λv1 + µw1 ) + . . . + anm (λvm + µwm )
a11 v1 + . . . + a1m vm
a11 w1 + . . . + a1m wm
.
.
+ µ
.
an1 v1 + . . . + anm vm
an1 w1 + . . . + anm wm
= λ
.
.
.
= λ(Av ) + µ(Aw ).
16 / 37
Lineare Gleichungssysteme und Matrizen
Beweis von Satz 4.1.
(i) a1 , . . . , am ∈ Kn die Spaltenvektoren von A ⇒
LA,0Kn =
λ1 , . . . , λm
λ1 a1 + . . . + λm am = 0Kn
Blatt 4 Aufgabe 2 ⇒ LA,0Kn ist Untervektorraum
(ii) 1. Fall: LA,b = ∅ ⇒ Behauptung
17 / 37
Lineare Gleichungssysteme und Matrizen
Beweis von Satz 4.1, Fortsetung.
2. Fall: LA,b 6= ∅
⇒ gibt v ∈ LA,b
w ∈ LA,0Kn ⇒
A(v + w ) = Av + Aw = b + 0Kn = b.
⇒ v + w ∈ LA,0Kn ⇒ v + LA,0Kn ⊆ LA,b
w ∈ LA,b ⇒
A(w − v ) = Aw − Av = b − b = 0Kn .
⇒ w − v ∈ LA,0Kn ⇒ w = v + (w − v ) ∈ v + LA,0Kn
18 / 37
Lineare Gleichungssysteme und Matrizen
Ziel: Lösungsverfahren für Lineare Gleichungssysteme
Denition (Elementare Zeilenumformungen einer Matrix)
A ∈ Kn×m , A = aij 16i6n,16j6m , ai = (ai 1 , . . . , aim ) der i -te
Zeilenvektor.
Zeilenvertauschung : Sei 1 6 r < s 6 n.
a1
..
.
ar −1
as
ar +1
ZVr ,s
A −−−→ ZVr ,s A = ...
as−1
ar
as+1
..
.
an
19 / 37
Lineare Gleichungssysteme und Matrizen
Denition (Elementare Zeilenumformungen einer Matrix,
Fortsetzung)
Multiplikation einer Zeile mit einem Skalar : Sei 1 6 r 6 n,
λ ∈ K.
a1
..
.
ar −1
ZMr (λ)
A −−−−→ ZMr (λ)A =
λar
ar +1
..
.
an
20 / 37
Lineare Gleichungssysteme und Matrizen
Denition (Elementare Zeilenumformungen einer Matrix,
Fortsetzung)
Addition des Vielfachen einer Zeile zu einer anderen :
1 6 s, r 6 n, λ ∈ K, s 6= r , ×: r < s .
a1
..
.
as−1
ZAr ,s (λ)
a
+
λa
A −−−−−→ ZAr ,s (λ)A =
s
r
as+1
..
.
an
21 / 37
Lineare Gleichungssysteme und Matrizen
Beispiel
1
2
3
4
5
A=
6
7
8
4
3
2
1
8
7
6
5
1
2
3
4
8
ZV2,4 A =
7
6
5
4
3
2
1
5
6
7
8
1
5
ZM3 (−2)A =
−8
2
3
4
6
7
8
−6 −4
8
∈ R4 × 4
7
6
−2
5
1
2
3
4
5
ZA1,3 (−1)A =
3
6
7
8
1
−1
8
7
6
−3
5
22 / 37
Lineare Gleichungssysteme und Matrizen
A ∈ Kn×m , b ∈ Kn
→ schreiben (A b) ∈ Kn×m+1 für Matrix A ergänzt um b als
(m + 1)-sten Spaltenvektor
Satz 4.3
A ∈ Kn×m , b ∈ Kn
A 0 = (A b) ∈ Kn×(m+1) . Ist A 00 = (A b) mit A ∈ Kn×m , b ∈ Kn
eine Matrix, die aus A 0 durch eine Folge von Anwendungen von
ZVr ,s für 1 6 r < s 6 n,
ZMr (λ) für 1 6 r 6 n, λ ∈ K \ {0}
ZAr ,s (λ) für 1 6 r , s 6 n, r 6= s , λ ∈ K
entsteht, so gilt
LA,b = LA,b
Matrix (A b) heiÿt auch erweiterte Koezientenmatrix des
Gleichungssystems Ax = b
23 / 37
Lineare Gleichungssysteme und Matrizen
Beispiel
1
5
A =
4
8
3 4
7 8
2 1
6 5
1 2
5 6
⇒ A 0 = (A b) =
4 3
8 7
2
6
3
7
b=
1
3
−1
1
3
7
2
6
4 1
8 3
1 −1
5 1
1
2
3
5
6
7
A 00 = ZM3 (−1)ZA1,4 (−1)A 0 =
−4 −3 −2
7
5
3
1
2
3 4
5
6
7 8
Satz 4.3
für =====⇒ A =
−4 −3 −2 1 b
7
5
3 1 0
LA,b = LA,b
4 1
8 3
1
1 0
1
=
3
1
0
gilt
24 / 37
Lineare Gleichungssysteme und Matrizen
Beweis von Satz 4.3.
Genügt zu zeigen : eine Anwendung von ZVr ,s , ZMr (λ), ZAr ,s (λ)
lässt die Lösungsmenge invariant
a1 , . . . , an Zeilenvektoren der Matrix A
ai = (ai 1 , . . . , aim ), 1 6 i 6 n,
denieren ai v = ai 1 v1 + · · · + aim vm Form der
Matrixmultiplikation
ZVr ,s : Sei (A b) = ZVr ,s (A b)
Av = b ⇔ a1 v = b1 , . . . , ar v = br , . . . , as v = bs , . . . , an v = bn
⇔ a1 v = b1 , . . . , as v = bs , . . . , ar v = br , . . . , an v = bn
⇔ Av = b
25 / 37
Lineare Gleichungssysteme und Matrizen
Beweis von Satz 4.3, Fortsetzung.
ZMr (λ), λ 6= 0K : Sei (A b) = ZMr (λ)(A b)
Av = b ⇔ a1 v = b1 , . . . , an v = bn
λ6=0
⇔ a1 v = b1 , . . . , λar v = λbr , . . . , an v = bn
⇔ Av = b
26 / 37
Lineare Gleichungssysteme und Matrizen
Beweis von Satz 4.3, Fortsetzung.
ZAr ,s (λ): Sei (A b) = ZAr ,s (λ)(A b)
Av = b ⇔ a1 v = b1 , . . . , an v = bn
⇔ a1 v = b1 , . . . , ar v = br , . . . , λar v + as v = λbr + bs ,
. . . , an v = bn
⇔ a1 v = b1 , . . . , ar v = br , . . . , (λar + as )v = λbr + bs ,
. . . , an v = bn
⇔ Av = b
27 / 37
Lineare Gleichungssysteme und Matrizen
Beispiel
0 1
1
A=
, b=
2 −4
2
Dann ist
A0 =
0 1 1
2 −4 2
Betrachte nun
2 −4 2
A −−−→
0 1 1
1
ZM1 2
1 −2 1
−−−−−→
0 1 1
ZA1,2 (2)
1 0 3
−−−−−→
= A 00
0 1 1
0 ZV1,2
1 0
3
, b=
Also: A =
0 1
1
28 / 37
Lineare Gleichungssysteme und Matrizen
Beispiel (Beispiel: Fortsetzung)
Damit ist
LA,b
v1
=
∈ R2
v2
3
=
1
3
=
+ {0R2 }
1
1v1 + 0v2 = 3
0v1 + 1v2 = 1
29 / 37
Lineare Gleichungssysteme und Matrizen
Denition
A = aij ∈ Kn×m . Wir sagen A ist in Zeilenstufenform , falls
es gibt ein 0 6 s 6 n, so dass der (s + 1)-ste, . . . , n-te
Zeilenvektor der Nullvektor ist und alle andere verscheiden
vom Nullvektor sind,
Ist 1 6 i 6 s , und ji der kleinste Index mit aiji 6= 0, dann ist
aiji = 1,
es gilt j1 < j2 < · · · < js .
A ist in reduzierter Zeilenstufenform , falls zusätzlich,
a1ji = · · · = ai−1 ji = 0 für 2 6 i 6 s .
30 / 37
Lineare Gleichungssysteme und Matrizen
Eine Matrix ist in Zeilenstufenform ,
Form ist:
0 ... 0
1
∗ ...
0 ... ... ... 0
1
..
.
..
.
0 ... ... ... ... ...
0 ... ... ... ... ...
..
.
0 ... ... ... ... ...
wenn sie von der folgenden
... ... ...
∗ ... ...
.. ..
.
.
0
1
∗
... ... ...
... ∗
... ∗
..
.
... ∗
... 0
..
.
... ... ... ... 0
31 / 37
Lineare Gleichungssysteme und Matrizen
Eine Matrix ist in reduzierter Zeilenstufenform , wenn sie von der
folgenden Form ist:
0
0
...
...
∗
... ... ...
0
1
...
...
∗
0
.
.
.
0
0
0
1
.
.
.
∗
∗
.
.
.
...
...
.
.
.
∗
∗
.
.
.
0
∗
∗
.
.
.
.
.
.
0
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
0
1
...
...
∗
...
...
...
...
...
...
...
...
...
...
...
...
...
.
.
.
0
∗
∗
.
.
.
... ∗
... 0
.
.
.
... 0
...
...
32 / 37
Lineare Gleichungssysteme und Matrizen
Data:
A∈
Kn×m ,
b∈
Gauÿ-Algorithmus
Kn
b1
..
A = (aij )16i6n,16j6m , b = .
bn
Dann ist
a11 . . . a1m b1
..
..
A 0 = A b = ...
.
.
an1 . . . anm bn
Result:
LA,b = ∅ oder falls LA,b 6= ∅, Reduzierte
Zeilenstufenform von A 0 = (A b)
33 / 37
Lineare Gleichungssysteme und Matrizen
z := 1.
while
Zeilen z, . . . , n sind nicht alles Nullzeilen
do
s der kleinste Spaltenindex, für den eine Zeile mit Index
z, . . . , n existiert, für die der Eintrag in Spalte s 6= 0 ist.
if
s = m + 1 then
return Lösungsmenge ∅
end
z 6 l1 < . . . < lr 6 n die Zeilenindizes > z , für die ein
Eintrag 6= 0K in Spalte s existiert
λi der Eintrag in Zeile li und Spalte s , 1 6 i 6 r
→ ZVz,l1 falls z 6= l1
→ ZMz λ11
→ ZAz,l2 (−λ2 ), . . . , ZAz,lr (−λr )
z := z + 1
end
A 0 ist jetzt in Zeilenstufenform
34 / 37
Lineare Gleichungssysteme und Matrizen
z := 2.
while
Zeile z nicht der Nullvektor und z 6= n + 1
do
s der kleinste Spaltenindex mit Eintrag 6= 0K in Zeile z
λ1 , . . . , λz−1 die Einträge in Spalte s in den Zeilen
1, . . . , (z − 1).
→ ZAz,1 (−λ1 ), ZAz,2 (−λ2 ), . . ., ZAz,(z−1) (−λz−1 )
z := z + 1
end
return A 0
A 0 ist in reduzierter
Zeilenstufenform
35 / 37
Lineare Gleichungssysteme und Matrizen
Beispiel
1
2 1 3 2
5
A = −1 −2 1 −1 0 , b = −1
2
4 2 6 0
12
1
2 1 3 2 5
1 2 1 3 2 5
ZA1,2 (1)
−1 −2 1 −1 0 −1 −−−−−−→ 0 0 2 2 2 4
ZA1,3 (−2)
2
4 2 6 0 12
0 0 0 0 −4 2
1
1 2 1 3 2 5
ZM2 2
−−−−−→ 0 0 1 1 1 2
0 0 0 0 −4 2
1
1 2 1 3 2 5
ZM3 − 4
−−−−−−→ 0 0 1 1 1 2
0 0 0 0 1 − 12
36 / 37
Lineare Gleichungssysteme und Matrizen
Beispiel (Beispiel: Fortsetzung)
1 2 1 3 2 5
1 2 0 2 1 3
ZA2,1 (−1)
0 0 1 1 1 2 −
−−−−−→ 0 0 1 1 1 2
1
0 0 0 0 1 −2
0 0 0 0 1 − 21
1 2 0 2 0 3 12
ZA3,1 (−1)
−−−−−−→ 0 0 1 1 0 2 12
ZA3,2 (−1)
0 0 0 0 1 − 21
37 / 37
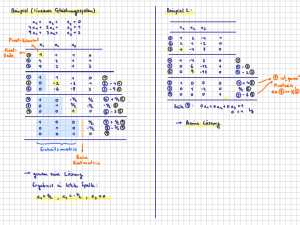
Lineare Gleichungssysteme und Matrizen
Beispiel
1 2 3 4
5
A = 4 3 2 1 , b = 10
2 4 6 8
8
1 2 3 4 5
1
ZA1,2 (−4)
4 3 2 1 10 −
−−−−−→ 0
ZA1,3 (−2)
2 4 6 8 8
0
1
1
ZM2 − 5
−−−−−−→ 0
0
2
3
4
5
−5 −10 −15 −10
0
0
0
−2
2 3 4 5
1 2 3 2
0 0 0 −2
Leere Lösungsmenge wegen 3. Zeile:
0 · x1 + 0 · x2 + 0 · x3 + 0 · x4 = −2.
38 / 37