Wirtschaftsmathematik - für International Management (BA)

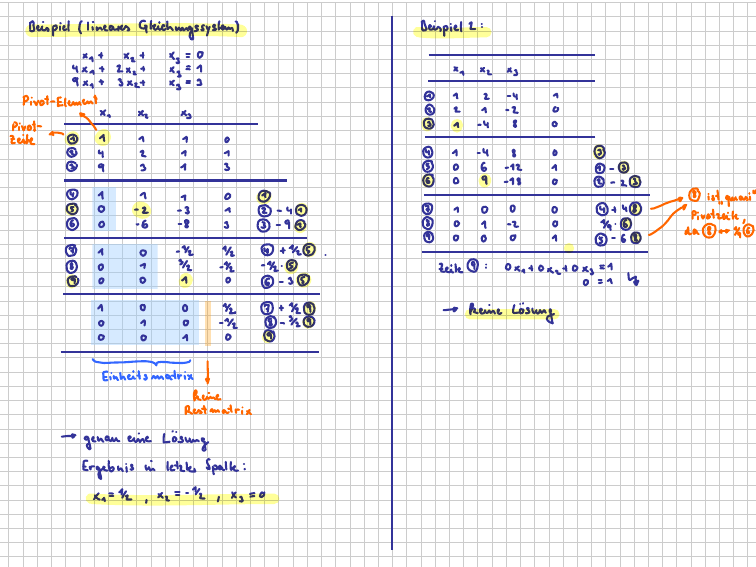
Wirtschaftsmathematik
für International Management (BA)
Wintersemester 2012/13
Stefan Etschberger
Hochschule Augsburg
Lösung von LGS
Mathematik
Stefan Etschberger
Elementare Umformungen
Das sind Umformungen der Koeffizientenmatrix, die die
Lösung nicht verändern. Erlaubt ist
Multiplikation einer Zeile mit beliebigen Zahlen c 6= 0
Addition einer Zeile zu einer anderen Zeile
Vertauschen von Zeilen oder Spalten
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
Lösungsalgorithmus
Lösung mit Verfahren von Gauß-Jordan:
Systematische Umformungen nach obigem
Prinzip, bis Darstellung der Koeffizientenmatrix in Einheits- und Restmatrix ensteht
Algorithmus und Lösungsvarianten
siehe Vorlesung
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
53
Invertierung von Matrizen
Mathematik
Stefan Etschberger
Definition
Gegeben: n × n-Matrix (quadratisch)
Existiert eine n × n-Matrix X mit AX = XA = E, so heißt X
die zu A inverse Matrix.
Schreibweise: X = A−1
⇒ AA
−1
−1
=A
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
A=E
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
Inverse Matrizen und Gleichungssysteme
4. Lineare Programme
Falls A−1 existiert, gilt:
5. Folgen und Reihen
6. Finanzmathematik
Ax = b
⇒
A−1 Ax = A−1 b
⇒
Ex = x = A−1 b
7. Reelle Funktionen
8. Differenzieren 1
Damit existiert genau eine Lösung und zwar:
9. Differenzieren 2
10. Integration
−1
x=A
b
54
BD
Aufgabe 38
Gegeben sind die Matrizen:
AD
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
˘
;
BD
1
1 1 1
1 1 0 0
1 0 1 0
1 0 0 1
a) Zeigen Sie, dass 12 A orthogonal ist.
b) Berechnen Sie B 1 .
c) Lösen Sie das Gleichungssystem AB x D c mit
x T D .x1 ; x2 ; x3 ; x4 / ; c T D .1; 2; 3; 4/
unter Verwendung von b).
˘
1
1 1 1
1 1 0 0
1 0 1 0
1 0 0 1
˘
LGS und Orthogonalität
Mathematik
Stefan Etschberger
Berechnung inverser Matrizen durch den Gaußalgorithmus:
Ansatz:
Ax +
Ey = 0
⇒ A−1 Ax + A−1 Ey = 0
⇒
Ex + A−1 y = 0
Also: Gaußtableau mittels elementarer Umformungen
folgendermaßen umformen:
(A|E) −→
E|A−1
Orthogonale Matrizen
Eine n × n-Matrix A heißt orthogonal, wenn gilt:
T
T
AA = A A = E
1. Grundlegende
Bausteine
2. Grundlegende
Werkzeuge
3. Lineare Algebra
3.1. Matrizen und Vektoren
3.2. Matrixalgebra
3.3. Lineare
Gleichungssysteme
3.4. Inverse Matrizen
4. Lineare Programme
5. Folgen und Reihen
6. Finanzmathematik
7. Reelle Funktionen
8. Differenzieren 1
9. Differenzieren 2
10. Integration
Bei orthogonalen Matrizen A gilt also: A−1 = AT .
Mit A ist damit auch AT orthogonal
55