Gemischte Übungen
Werbung
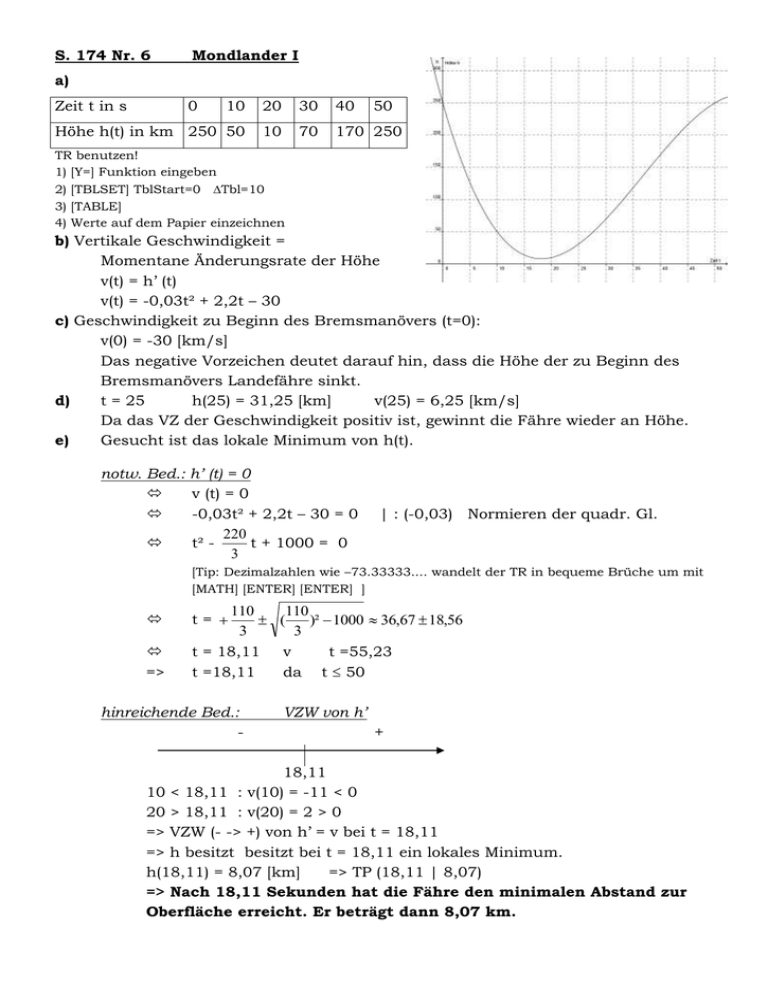
S. 174 Nr. 6 Mondlander I a) Zeit t in s 0 10 20 30 40 50 Höhe h(t) in km 250 50 10 70 170 250 TR benutzen! 1) [Y=] Funktion eingeben 2) [TBLSET] TblStart=0 Tbl=10 3) [TABLE] 4) Werte auf dem Papier einzeichnen b) Vertikale Geschwindigkeit = Momentane Änderungsrate der Höhe v(t) = h’ (t) v(t) = -0,03t² + 2,2t – 30 c) Geschwindigkeit zu Beginn des Bremsmanövers (t=0): v(0) = -30 [km/s] Das negative Vorzeichen deutet darauf hin, dass die Höhe der zu Beginn des Bremsmanövers Landefähre sinkt. d) t = 25 h(25) = 31,25 [km] v(25) = 6,25 [km/s] Da das VZ der Geschwindigkeit positiv ist, gewinnt die Fähre wieder an Höhe. e) Gesucht ist das lokale Minimum von h(t). notw. Bed.: h’ (t) = 0 v (t) = 0 -0,03t² + 2,2t – 30 = 0 220 t² t + 1000 = 0 3 | : (-0,03) Normieren der quadr. Gl. [Tip: Dezimalzahlen wie –73.33333.... wandelt der TR in bequeme Brüche um mit [MATH] [ENTER] [ENTER] ] => 110 110 ( )² 1000 36,67 18,56 3 3 t = 18,11 v t =55,23 t =18,11 da t 50 t= hinreichende Bed.: - VZW von h’ + 18,11 10 < 18,11 : v(10) = -11 < 0 20 > 18,11 : v(20) = 2 > 0 => VZW (- -> +) von h’ = v bei t = 18,11 => h besitzt besitzt bei t = 18,11 ein lokales Minimum. h(18,11) = 8,07 [km] => TP (18,11 | 8,07) => Nach 18,11 Sekunden hat die Fähre den minimalen Abstand zur Oberfläche erreicht. Er beträgt dann 8,07 km. S. 174 Nr. 8 Blutspiegel eines Medikaments a) Beim Zeichnen des Graphen den TR benutzen! 1) [Y=] Funktion eingeben 2) [TBLSET] TblStart=0 Tbl=1 3) [TABLE] 4) Werte auf dem Papier einzeichnen Dem Graphen ist zu entnehmen, dass die Konzentration zur Zeit der Einnahme etwa 80 µg/ml beträgt und das Medikament nach ca. 9 h gänzlich abgebaut ist. b) Berechnung der Maximalkonzentration: Berechne lok. Extrema von c: notw. Bed.: c’ (t) = 0 c’(t) = 3 t² - 34 t + 63 3 t² - 34 t + 63 = 0 34 t² + 21 = 0 3 t= |:3 Normieren der quadr. Gl. 17 17 17 10 ( )² 21 3 3 3 3 [Tip: Dezimalzahlen wie 3.33333.... wandelt der TR in bequeme Brüche um mit [MATH] [ENTER] [ENTER] ] 7 2,33 v 3 hinr. Bed.: VZW von c’ + - t= t= 2,33 0 < 7/3: c’(0) = 63 > 0 7/3 < 3 < 9:c’(3) = -12 < 0 10 > 9: c’(10) = 23 > 0 7 => VZW (+ -> -) von c’ bei t = 3 27 9 3 + 9 => c besitzt bei t = 7 ein lokales Maximum. 3 7 7 ) = 148,15 [µg/ml] => HP( | 148,15) 3 3 2,33 h = 2 h 20 min => Die Maximalkonzentration wird nach etwa 2 h 20 min erreicht und beträgt 148,15 µg/ml. Im Zeitintervall [0 h | 2,33 h] steigt die Konzentration, im Zeitintervall [2,33 h | 9 h] fällt sie wieder. c( c) Gesucht ist das Extremum der Ableitungsfunktion bzw. die Wendestelle: (verringert sich die Konzentration am stärksten) => c’ => Extremum c’’ (t) = 6t – 34 notw. Bed.: c’’(t) = 0 6t – 34 = 0 6t = 34 17 t= 5,67 [h]= 5 h 40 min 3 hinr. Bed.: VZW von c’’ + 5 h 40 min 17 : c’’(0) = -34 < 0 3 17 9> : c’’(9) = 20 > 0 3 => VZW ( - > +) von c’’ 17 => c besitzt bei t = eine Wendestelle 3 17 bzw. c’ besitzt bei t = ein lokales Minimum 3 => Bei t = 5 h 40 min verringert sich die Konzentration am stärksten 0< S. 175 Nr. 1 Funktionsunterschung a) 1) Ableitungen: 1 1 1 1 f(x) = x(x-6)² = x (x² - 12 x + 36) = (x³ - 12 x² + 36 x) = x³ - 2x² + 6 x 6 6 6 6 [Ausmultiplizieren notwendig, um f ableiten zu können. Das Ergebnis sollte unbedingt mit dem TR überprüft werden: Funktion aus Aufgabenstellung Ergebnis ( 1 x(x-6)² bei Y1 eingeben, das selbst berechnete 6 1 x³ - 2x² + 6 x )bei Y2. Funktionen mit [GRAPH] anzeigen lassen. Evtl. 6 sichtbaren Bereich anpassen mit [ZOOM] -> 6ZStandart. Ist nur ein Graph zu sehen, hat man wahrscheinlich richtig gerechnet] f ’ (x) = ½ x²- 4x + 6 [Auch hier bietet sich eine Kontrolle mit dem TR an: Bei Y1 = nDerive(1/6*x*(X²-12X+36) , X, X) eingeben, bei Y2 das berechnete Ergebnis (Y2 = ½ x²- 4x + 6). Wieder mit [GRAPH] beide Graphen auf Übereinstimmung überprüfen. nDerive findet man unter [MATH] -> 8] f ‘’ (x) = x – 4 2) Nullstellen: f(x) = 0 1 x(x-6)² = 0 6 x=0 v (x-6)² = 0 x=0 v x-6 = 0 x=0 v x=6 f besitzt Nullstellen bei 0 und bei 6. 3) Extrema: notw. Bed.: f’(x) = 0 ½ x²- 4x + 6 = 0 | 2 x² - 8x + 12 = 0 x = +4 x=2 4² 12 = 4 2 v x=6 hinr. Bed.: VZW von f’ + 0 < 2: 0<4<6: 7 > 6: Normieren der quadr. Gl. 2 f’(0) = 6 > 0 f’(4) = -2 < 0 f’(7) = 2,5 > 0 - + 6 [Die Funktionswerte sollten nicht einzeln berechnet werden, sondern: Mit Y1 = ½ x²- 4x + 6 f’(x) eingeben ->[TBLSET] TblStart=0 Tbl = 1 -> [TABLE] Wertetabelle anzeigen lassen. Stimmen die berechneten Nullstellen von f’ mit den Tabellenwerten überein? (Achtung: Statt 0 schreibt der Rechner möglicherweise 1.7E-7, also 1,710-7 0. Davon sich nicht beirren lassen!) Dann die anderen 3 Werte der Tabelle entnehmen.] f(2) 5,33 f(6) = 0 => VZW (+ -> - ) von f’ bei x = 2 => f besitzt bei x = 2 ein lok. Maximum. HP (2 | 5,33) => VZW (- -> + ) von f’ bei x = 6 => f besitzt bei x = 6 ein lok. Minimum. TP (6 | 0) 4) Wendepunkte Notw. Bed.: f ’’ (x) = 0 x–4=0 x=4 Hinr. Bed.: VZW von f’’ Alternative 1: - 0< 5> f(4) => => + 4 4: f’’(0) = -4 < 0 4: f’’(5) = 1 > 0 2,67 VZW (- -> +) von f’’ bei x = 4 WP(4 | 2,67) => f besitzt bei x = 4 eine Wendestelle Alternative 2: Da f’’(x) eine lineare Funktion ist, muss bei der Nullstelle ein VZW stattfinden. f(4) 2,67 => WP(4 | 2,67) b) g(x) = 6x => Steigung von g: m = 6 Suche die Stellen von f, an denen die Ableitung gleich der Steigung von g ist: f’(x) = 6 ½ x²- 4x + 6 = 6 ½ x²- 4x = 0 x² - 8x = 0 x (x – 8) = 0 (Zum Nullstellenfinden bietet sich hier die Linearfaktorisierung an) x=0 v x-8 = 0 x=0 v x=8 f(0) = 0 f(8) = 5,33 g(0) = 0 => g hat den Punkt (0 | 0) mit f gemeinsam und die Steigung von g und f beträgt dort 6. => Somit ist g Tangente an den Graphen von f im Punkt (0 | 0). Suche die parallele Tangente: y = f(8) = 5,33 m=6 y = mx + n n = y – mx = 5,33 - 68 = -42,67 => g2(x) = 6x – 42,67 ist eine parallele Tangente zu g(x). c) Ursprungssgerade: h(x) = mx (n = 0) Gemeinsamer Punkt = Schnittpunkt h(x) = f(x) 1 mx = x³ - 2x² + 6 x 6 1 x³ - 2x² + 6 x - mx = 0 |6 6 x³ - 12x² + 36 x - 6mx = 0 x(x² - 12 x + (36-6m) ) = 0 x=0 v x² - 12 x + (36-6m) = 0 x=0 v x = +6 6² (36 6m) Anzahl der Lösungen hängt von der Diskriminante (Rechenausdruck unter der Wurzel) ab: 6² - (36 – 6m) = 36 – 36 + 6m = 6m Ist die Diskriminante 6m, also m < 0, negativ, so gibt es nur eine Lösung (x = 0). Ist 6m = 0, also m = 0, so gibt es zwei Lösungen (x = 0 bzw. x = 6) Ist 6m > 0, also m > 0, so gibt es drei Lösungen. S. 176 Nr. 5 Funktionsuntersuchung f(x) = (x² - 1)² = x4 – 2x² + 1 g(x) = -(x² - 1)(x+1) = -(x3+x²-x-1) = -x³ - x² + x + 1 [Überprüfung mit dem TR: Sind gegebene und berechnete Funktionsgraphen deckungsgleich?) a) Da f nur gerade Exponenten besitz ist f eine achsensymmetrische Funktion. Da g sowohl gerade, als auch ungerade Exponenten besitzt, ist g weder symmetrisch zur y-Achse noch zum Ursprung. Der gegebene Graph, der z. B. ein lok. Max bei x = 0 besitzt, ist also f. b) Schnittpunkt mit der y-Achse : x = 0 g(0) = 1 P(0 | 1) g’(x) = -3x² - 2x + 1 g’(0) = 1 y=1 m=1 y = mx + n n = y –mx = 1 - 10 = 1 t:y=x+1 c) Steigung im Punkt P : m = g’(0) = 1 g’(x) = 1 -3x² - 2x + 1 = 1 -3x² - 2x = 0 x(-3x – 2) = 0 (Zum Nullstellenfinden bietet sich hier die Linearfaktorisierung an) x=0 v -3x – 2 = 0 x=0 v 3x = -2 x=0 v x = -2/3 g(-2/3) = 5/27 (-2/3|5/27) ist ein weiterer Punkt auf dem Graphen von g mit der gleichen Steigung 1. d) g’(x) = -20 -3x² - 2x + 1 = -20 -3x² - 2x + 21 = 0 | :(-3) x² +2/3x – 7 = 0 1 8 1 1 x = - ( )² 7 =- 3 3 3 3 x = 7/3 v x = -9 Bei x = 7/3 und x = -9 hat der Graph die Steigung –20. S. 176 Nr. 6 Wurf auf dem Mond a) f(1) = 31,2 [m] Nach einer Sekunde befindet sich der Stein in 31,2 m Höhe. b) f(t) = 50 -0,8 t² + 30 t + 2 = 50 -0,8 t²+ 30t –48 = 0 t² - 37,5t + 60 =0 |:(-0,8) t = 18,75 18,75² 60 18,75 17,08 t = 1,67 v t = 35,83 Nach 1,67 s und nach 35,83 s befindet sich der Stein in 50 m Höhe. c) Gesucht ist das Maximum der Höhe f(t). Alternative 1: f’(t) = -1,6 t + 30 notw. Bed.: f’(t) = 0 -1,6 t + 30 = 0 1,6t = 30 t = 18,75 hinr. Bed.: VZW von f’ + - 18,75 0 < 18,75: f’(0) = 30 > 0 20 > 18,75: f’(20) = -2 < 0 f(18,75) = 283,25 => VZW (+ -> -) von f’ bei x = 18,75 => f besitzt bei x = 18,75 ein lokales Maximum. => HP (18,75 | 283,25) Nach 18,75 s erreicht der Stein die Gipfelhöhe 283,25 m. Alternative 2: Da der Stein sich nach 1,67s und 35,83 s auf 50 m Höhe befindet, befindet er sich in der Mitte zwischen den beiden Zeitpunkten an seinem höchsten Punkt: t = 18,75 s. f(18,75) = 283,25 Nach 18,75 s erreicht der Stein die Gipfelhöhe 283,25 m. d) Gesucht: Nullstelle von f. f(t) = 0 -0,8 t² + 30 t + 2 = 0 |:(-0,8) t² - 37,5 – 2,5 = 0 t = 18,75 18,75² 2,5 18,75 18,82 => t = 37,57 [s] da t > 0 (Die zweite Lösung ist negativ, da der Astronaut zu Beginn den Stein in der Hand, also über dem Boden hält). Die Flugzeit des Steins dauert 37,57 s. e) Die Geschwindigkeit entspricht der Ableitung f’. f’(37,57) = -30,112 S. 176 Nr. 7 Wasserstand a) Beim Zeichnen des Graphen den TR benutzen! 1) [Y=] Funktion eingeben 2) [TBLSET] TblStart=0 Tbl=1 3) [TABLE] 4) Werte auf dem Papier einzeichnen b) Gesucht ist die durchschnittliche Änderungsrate im Intervall [0 | 100]. h(0) = 120 h(100) = 3,33 h(100) h(0) 3,33 120 1,17 => 100 0 100 Im Mittel fällt der Wasserstand um 1,17 Meter pro Tag. c) Gesucht: momentane Änderungsrate für t = 0 und t = 50 1 f ’ (t) = t–2 f’(0) -2 f’(50 ) -1,17 60 Am Anfang der Trockenperiode sinkt der Wasserstand um 2 Meter pro Tag, in der Mitte sinkt er um 1,17 Meter pro Tag. d) Gesucht ist die Stelle mit f’(t) = -1 1 t – 2 = -1 60 1 t=1 60 t = 60 Nach 60 Tagen fällt der Wasserstand nur noch um 1 Meter pro Tag. e) f(t) = 7,5 1 t² - 2t + 120 = 7,5 120 1 t² - 2t +112,5 = 0 120 t² - 240 t + 13500 = 0 |120 120² 13500 = 120 30 t = 120 => t = 90 v t = 150 t = 90 da t 100 Nach 90 Tagen fällt der Wasserstand unter die kritische 7,5-Marke. f) f(t) = 0 1 t² - 2t +120 = 0 120 t² - 240 t + 14400 = 0 t = 120 |120 120² 14400 = 120 => Nach 120 Tagen wäre der See völlig leer. Nullstellen, Extrema und Wendestellen mit Geogebra a) Beschreibe anhand der linken Abbildung eine Möglichkeit, mit Geogebra Extrema und Wendestellen zu ermitteln. b) Beschreibe anhand der rechten Abbildung eine andere Möglichkeit, mit Geogebra Extrema und Wendestellen zu ermitteln. c) Beschreibe, eine dritte Möglichkeit, Wendestellen zu ermitteln. Geogebra-Befehle: Ableitung[ ... ] Nullstelle[ ... ] Nullstellen, Extrema und Wendestellen mit Geogebra a) Beschreibe anhand der linken Abbildung eine Möglichkeit, mit Geogebra Extrema und Wendestellen zu ermitteln. b) Beschreibe anhand der rechten Abbildung eine andere Möglichkeit, mit Geogebra Extrema und Wendestellen zu ermitteln. c) Beschreibe, eine dritte Möglichkeit, Wendestellen zu ermitteln. Geogebra-Befehle: Ableitung[ ... ] Nullstelle[ ... ]