Die Umkehrfunktion der e-Funktion

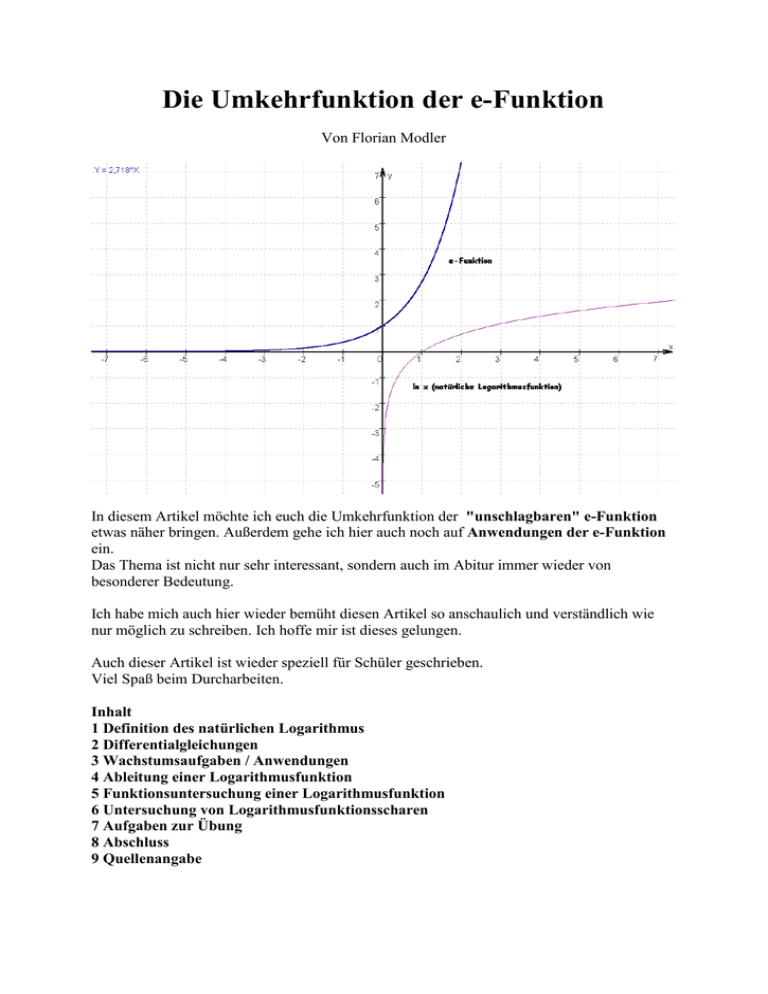
Die Umkehrfunktion der e-Funktion
Von Florian Modler
In diesem Artikel möchte ich euch die Umkehrfunktion der "unschlagbaren" e-Funktion
etwas näher bringen. Außerdem gehe ich hier auch noch auf Anwendungen der e-Funktion
ein.
Das Thema ist nicht nur sehr interessant, sondern auch im Abitur immer wieder von
besonderer Bedeutung.
Ich habe mich auch hier wieder bemüht diesen Artikel so anschaulich und verständlich wie
nur möglich zu schreiben. Ich hoffe mir ist dieses gelungen.
Auch dieser Artikel ist wieder speziell für Schüler geschrieben.
Viel Spaß beim Durcharbeiten.
Inhalt
1 Definition des natürlichen Logarithmus
2 Differentialgleichungen
3 Wachstumsaufgaben / Anwendungen
4 Ableitung einer Logarithmusfunktion
5 Funktionsuntersuchung einer Logarithmusfunktion
6 Untersuchung von Logarithmusfunktionsscharen
7 Aufgaben zur Übung
8 Abschluss
9 Quellenangabe
1 Definition des natürlichen Logarithmus
Die Umkehrfunktion der e-Funktion bezeichnet man als natürliche Logarithmusfunktion.
y  ex
x  ey
y  log e x
Definition:
Der Logarithmus loge zur Basis e heißt natürlicher Logarithmus („logarithmus
naturalis“).
Er wird mit ln bezeichnet:
ln x  log e x
Die Funktion f ( x)  ln x nennt man natürliche Logarithmusfunktion.
2 Differentialgleichungen
Wie leitet man die Exponentialfunktion f ( x)  b x ab?
Lösung:
Man wendet folgendes Logarithmusgesetz an: blogb x  x
eln b  b | (...) x
Dies wird mit x potenziert und wir erhalten:
(eln b ) x  b x
Substitution von ln b  k :
ekx  b x  f ( x)
Bildung der Ableitung:
k  ekx  f '( x)
Rücksubstitution k  ln b :
ln b  (eln b ) x  f '( x)
f '( x)  ln b  b x
Regel:
f ( x)  b x mitx 

/{1} hat für jedes x 
die Ableitung f '( x)  ln b  b x .
Die Ableitung der Funktion f ( x)  ekx ist f '( x)  k  ekx .
Eine solche Gleichung, in der eine Funktion sowie ihre Ableitung (allgemeiner: Ableitungen)
vorkommen, heißt eine Differentialgleichung.
Lösung einer Differentialgleichung sind also Funktionen. Zum Beispiel ist die Funktion
f ( x)  ekx eine Lösung der Gleichung f '  k  f .
Bei einer Differentialgleichung interessieren sämtliche Lösungen, das heißt die gesamte
Lösungsmenge. Gibt es weitere Lösungen f’=kf außer den bekannten Lösungen
f ( x)  a  ekx ? Man kann beweisen, dass die Gleichung f’=kf außer den eben genannten keine
weiteren Lösungen hat.
Satz:
Die Differentialgleichung f’=kf mit k 
besitzt genau die Lösungen x  a  ekx (a  ) .
Beweis:
Es sei u irgendeine Lösung der Differentialgleichung. Dann gilt: u '( x)  k  u ( x) .
u ( x)
Wir bilden die Ableitung des Quotienten f ( x)  kx nach der Quotientenregel (siehe oben):
e
kx
kx
u '( x)  e  ke  u ( x)
. Einsetzen von u '( x)  k  u ( x) ergibt:
f '( x) 
(ekx )²
k  u ( x)  ekx  kekx  u ( x)
0
f '( x) 
 kx  0( x  ) .
kx
(e )²
(e )²
u ( x)
Die Quotientenfunktion kx hat für alle x  die Ableitung 0, sie ist also konstant gleich a
e
u ( x)
mit a : kx  a . Daraus folgt: u( x)  a  ekx .
e
Jede Lösung der Differentialgleichung hat also die Gestalt x  a  e kx .
Da sich jede Exponentialfunktion in der Form f ( x)  a  ekx (a  0, k  ) darstellen lässt,
kann man wegen dem oben angeführten Satz auch sagen:
f’=kf ist die Differentialgleichung der Exponentialfunktion.
3 Wachstumsaufgaben / Anwendungen
Viele Anwendungssituationen können durch Differentialgleichungen beschrieben werden. Ein
Beispiel dafür ist der radioaktive Zerfall.
Radioaktive Präparate zerfallen so, dass die Zerfallsgeschwindigkeit proportional zur jeweils
vorhandenen Masse des Präparats ist. Bezeichnet t die Zeit und gibt N(t) die zum Zeitpunkt t
vorhandene Masse an, so ist die Zerfallsgeschwindigkeit gleich der Ableitung N’(t).
Das Zerfallsgesetz lautet dann also N '(t )  k  N (t ) mit einer gewissen für das gegebene
radioaktive Präparat typischen Konstanten k. Da bei ist k negativ, da die Masse im Laufe der
Zeit abnimmt.
Ein Beispiel in Form einer Aufgabe.
Das Zerfallsgesetz für das Radium A lautet N '(t )  k  N (t ) . Wird t in Minuten gemessen, so
1
) . N(t) werde in mg gemessen. Die zur Zeit t=0 vorhandene Masse
ist k  0, 227(in
min
betrage N (0)  N0 .
a) Berechne die Zerfallsfunktion t  N (t ) .
b) Berechne denjenigen Zeitpunkt tH, an dem nur noch die Hälfte der Anfangssubstanz N0
vorhanden ist. Überlege dann: Wann ist nur noch ein Viertel von N0 vorhanden.
Veranschauliche dies im Graphen von t  N (t ) .
c) Ab wann sind nur noch weniger als 10% von N0 vorhanden?
d) Berechne die Zerfallsgeschwindigkeit N’(t). Wie groß ist diese Geschwindigkeit nach 5
min?
Lösungen:
a) Nach dem oben angeführten Satz gilt N (t )  a  ekt mit einem gewissen a
a=N(0) gilt a  N 0 , somit N (t )  N 0  e kt mit k  0, 227 .
b) Zum Zeitpunkt tH soll gelten N (t H ) 
. Wegen
N0
N
, also N 0  e ktH  0 und somit:
2
2
1
2
Wir logarithmieren auf beiden Seiten, um tH zu isolieren:
1
ln e ktH  ln
2
1
ln
Wegen ln e ktH  kt H gilt somit t H  2  3, 05 .
k
tH ist also abhängig von der Anfangssubstanz N0.
1
Nun gilt: e k (t tH )  e kt  e ktH  e kt  .
2
Die vorhandene Substanz geht demnach jedes Mal auf die Hälfte zurück, wenn t um tH
wächst. (Dies ist eine Grundeigenschaft der Exponentialfunktion (siehe oben)).
e ktH 
Daher ist zum Zeitpunkt 2tH, also nach ungefähr 6,1 Minuten, nur noch die Masse
N0
4
vorhanden.
Der Zeitpunkt tH, zu dem die Anfangssubstanz N0 auf die Hälfte zurückgegangen ist, heißt
Halbwertszeit des radioaktiven Präparates. Die Halbwertszeit von Radium A beträgt
demnach ungefähr 3 Minuten und 3 Sekunden.
c) Zum Zeitpunkt t, zu dem noch genau 10% der Anfangssubstanz vorhanden ist, gilt:
N (t )  0,1  N 0 , d .h.e kt  0,1
ln 0,1
 10,14
Logarithmieren liefert wie oben: t H 
k
Nach etwas mehr als 10 Minuten sind also weniger als 10% der Anfangssubstanz vorhanden.
d) Die Zerfallsgeschwindigkeit beträgt N '(t )  kN 0 e kt (in
mg
) . Für t=5 gilt also
min
N '(5)  0, 027 N 0 e 1,135  0, 073N 0 .
Die Geschwindigkeit ist negativ, da die Substanz abnimmt.
4 Ableitung einer Logarithmusfunktion
Die Ableitung einer Logarithmusfunktion möchte ich an dieser Stelle nicht herleiten, sondern
jedem User es selber überlassen:
Satz:
Die natürliche Logarithmusfunktion f ( x)  ln x hat für jedes x 
1
f '( x )  .
x
Satz:
Die Logarithmusfunktion f ( x)  log b x(b 
1
f '( x) 
.
ln b  x


/{1}) hat für jedes x 
die Ableitung

die Ableitung
5 Funktionsuntersuchung einer
Logarithmusfunktion
Untersuche die Funktion f ( x)  2 x (ln x  1) .
1. Definitionsbereich:
Da ln x nur für x>0 definiert ist, und da negative Wurzeln in der Menge der reellen Zahlen
nicht definiert sind, ist D   .
2. Verhalten für betragsgroße x:
Für x   geht f ( x)   , da
2 x (ln x  1) gegen  strebt.
3. Symmetrie:
Für Achsensymmetrie müsste gelten f(-x)=f(x)
Prüfen von f(-1)=f(1):
2 1(ln  1  1)  2 1(ln1  1) Dies ist eine falsche Aussage, außerdem ist nicht alles
definiert.
Somit liegt keine Achsensymmetrie vor.
Für Punktsymmetrie müsste gelten f(-x)=-f(x)
Prüfen von f(-1)=-f(1):
2 1(ln  1  1)  2 1(ln1  1) Dies ist eine falsche Aussage, außerdem ist nicht alles
definiert.
Somit liegt keine Punktsymmetrie vor.
Daraus kann man schließen, dass der Graph weder achsensymmetrisch noch
punktsymmetrisch ist.
4. Gemeinsame Punkte mit den Koordinatenachsen:
-x=0
f (0)  2 0(ln 0  1)  0
S (0 / 0)
 f ( x)  0
0  2 x (ln x  1) |: 2 x
0  ln x  1| 1
1  ln x | e
x  e  2, 72
5. Ableitungen:
f ( x)  2 x (ln x  1)
f
f
f
f
f
4 32
1
'( x)  x  (ln x  1)  2 x 
3
x
3
4
1 4 3 1
1
''( x)  2 x  (ln x  1)  x 2   x 2   2 x  ( )
3
x 3
x
x²
3
4
1
1
''( x)  2 x 2   2 x  (ln x  1  )
3
x
x²
3
8
1
1
''( x)  x 2   2 x  (ln x  1  )
3
x
x²
3
1 8 2
1
4 32
1
1
1
'''( x)  4 x   x  ( )  x  (ln x  1  )  2 x  (  2 )
x 3
x² 3
x²
x
x³
6. Extrema:
Notwendige Bedingung für das Vorhandensein eines Extrema: f '( x)  0 :
4
1
x  x  (ln x  1)  2 x  |: x
3
x
4
1
0  x  (ln x  1)  2  |  x
3
x
4
0  x ²  (ln x  1)  2 | 2
3
4
3
2  x ²  (ln x  1) | 
3
4
3
  x ²  (ln x  1) | e |: x ²
2
0
e
3
  x 2
2
3
  x 2
 e(ln x 1)
e 2  x 1
x  0, 37
Hinreichende Bedingung für das Vorhandensein eines Extrema: f '( x)  0  f ''( x)  0 :
f ''(0,37)  0 : Minimum
T (0,37 /  2, 43)
7. Wendestellen:
Notwendige Bedingung für das Vorhandensein eines Extrema: f ''( x)  0 :
8 3 1
1
0  x 2   2 x  (ln x  1  ) |: x
3
x
x²
8
1
1
0  x   2  (ln x  1  )
3
x
x²
8
2
2
0   ln x ²  2  | 2 
3
x²
x²
2 8
8
2    ln x ² | 
x² 3
3
2 2
   ln x ² | e
3 x²
2 2
 
e 3 x ²  x²
x  2, 72
Hinreichende Bedingung für das Vorhandensein eines Extrema: f ''( x)  0  f '''( x)  0 :
f '''(2, 72)  0
W (2, 72 / 6)
8. Wertebereich:
W  { y | y  2, 43}
6 Untersuchung von
Logarithmusfunktionsscharen
Untersuche die f k ( x)  ln( x²  k ); k  0 .
1. Definitionsbereich:
D
2. Symmetrie:
Wir haben die Vermutung, dass Achsensymmetrie vorliegt. Somit müssten wir f(-x)=f(x)
nachweisen:
f k ( x)  f k ( x)
ln(( x)²  k )  ln( x ²  k )
ln( x ²  k )  ln( x ²  k )
Daraus folgt, dass der Graph achsensymmetrisch ist.
3. Verhalten für betragsgroße x:
Für x   geht f ( x)   , da
x²  k gegen   geht und somit geht ln( x ²  k ) ebenfalls gegen   .
Für x   geht f ( x)   , da
x²  k gegen   geht und somit geht ln( x ²  k ) ebenfalls gegen   .
Oder man verweist auf die Achsensymmetrie.
4. Gemeinsame Punkte mit den Koordinatenachsen:
- x=0
f (0)  ln( x ²  k )  ln k
S y (0 / ln k )
- Nullstellen: f(x)=0
0  ln( x ²  k ) | e
1  x²  k
1  k  x ² | ...
x1,2    1  k
Fürk  1: eineNullstellebeix  0
Für 0  k  1: 2 Nullstellenbeix1,2    1  k
Fürk  1: keineNullstellen
5. Ableitungen:
1
2x
 2x 
x²  k
x²  k
2( x ²  k )  2 x  2 x 2( x ²  k )  4 x ² 2 x ²  2k  4 x ² 2 x ²  2k
f ''( x) 



( x ²  k )²
( x ²  k )²
( x ²  k )²
( x ²  k )²
(4 x)( x ²  k )  (2 x ²  2k )  2( x ²  k )  2 x
f '''( x) 
( x²  k )4
4 x( x ²  k )  4 x(2 x ²  2k )
f '''( x) 
( x ²  k )³
6. Extrema:
f k ( x)  ln( x ²  k ); f '( x) 
Notwendige Bedingung für das Vorhandensein eines Extrempunktes f '( x)  0 :
2x
0
x²  k
0  2x
x0
Hinreichende Bedingung für das Vorhandensein eines Extrempunktes f '( x)  0  f ''( x)  0 :
2k
f ''(0) 
, dak  0 : 0 : Minimum
k²
f (0)  ln k
T (0 / ln k )
7. Wendestellen:
Notwendige Bedingung für das Vorhandensein eines Extrempunktes f ''( x)  0 :
2 x ²  2k
| ( x ²  k )²
( x ²  k )²
0  2 x ²  2k
0
x  k
Hinreichende Bedingung für das Vorhandensein eines Extrempunktes f '( x)  0  f ''( x)  0 :
f '''( k ) 
4 k  2 k
0
(2k )³
f '''( k ) 
4 k  2k
0
(2k )³
W1 ( k / ln 2k );W2 (  k / ln 2k )
8. Wertebereich:
W  { y | y  ln k}
7 Aufgaben zur Übung
Aufgaben, die sich auf die vorangegangene Funktionsuntersuchung beziehen:
1. Auf welcher Linie liegen alle Wendepunkte der Funktion dieser Schar?
2. Haben verschiedene Funktionsscharen gemeinsame Punkte?
2. Haben verschiedene Funktionsscharen gemeinsame Punkte?
Lösungen:
1.
Der rechte Wendepunkt hat die Koordinaten x  k und y  ln 2k .
Nun forme ich x  k nach k um:
x k |²
k  x²
, dies setze ich in y  ln 2k :
y  ln(2 x ²)
Aus den Koordinaten des linken Wendepunktes erhält man ebenfalls y  ln(2 x ²) .
Also liegen alle Wendepunkte auf dem Graphen y  ln(2 x ²) .
2.
Haben verschiedene Graphen der Funktionsschar, etwa zu den Funktionen fk und fs einen
gemeinsamen Punkt, so gilt an dieser Stelle x:
f k ( x)  f s ( x)
ln( x ²  k )  ln( x ²  s) | e
x²  k  x²  s
ks
Also haben die Funktionen der Schar nur bei gleichen Parametern gemeinsame Punkte: Sie
stimmen dann aber völlig überein.
Graphen mit verschiedenen Parametern haben keine gemeinsamen Punkte.
8 Abschluss
So das war nun mein zweiter Teil zur e-Funktion.
Ich hoffe, ihr habt diesen Artikel mit Freude und Eifer gelesen und freut euch schon auf
meinen zweiten Teil.
Die Idee zu diesem Artikel entspringt der Arbeitsgruppe „Schulmathematik“.
9 Quellenangabe
Ich habe mich sehr an mein wunderschönes, ausführliches und verständliches Schulbuch
gehalten. Hier zu kaufen:
Florian Modler