Document

1. Produktionstechnologien
Die Produktionsfunktion y=f(a,b) gibt an, wie viel man mit einer gegebenen Inputmenge (a,b) maximal vom
Gute Y herstellen kann. Die Produktionsfunktion gibt damit immer das Ergebnis eines technisch effizienten
Produktionsprozesses an.
Beispiele:
y = a+b
y  a 0,5  b 0,5
y = min {a,b}
Die klassischen Inputfaktoren sind Arbeit, Boden, Rohstoffe und Kapital. Heute wird außerdem explizit das
Humankapital genannt. Eine Produktionsfunktion kann bei maximal zwei Inputfaktoren grafisch durch
Isoquanten dargestellt werden. „Eine Isoquante ist die Menge aller möglichen Kombinationen der Inputs 1 und
2, die gerade ausreicht, um eine vorgegebene Menge des Outputs zu erzeugen.“
Grundsätzlich können Produktionstechnologien limitational oder (vollkommen oder begrenzt) substitutiv sein.
Beispiele: Isoquanten verschiedener Produtkionsfunktionen:
1.1 Eigenschaften von Produktionsfunktionen
Gewöhnlich werden Produktionsfunktionen folgende Eigenschaften unterstellt:

Monotonie: Nach einer Erhöhung der Einsatzmenge eines Faktors ist die Outputmenge mindestens
genauso hoch wie zuvor:
y (a  a, b  b)  y (a, b)

Konvexität: Die Mischung zweier Faktorkombinationen, welche auf der gleichen Isoquanten liegen führt
zu mindestens dem gleichen Output wie jede der beiden Faktorkombinationen für sich.
  y(a1 , b1 )  (1   )  y(a2 , b2 )  y(a1 , b1 ) Das Grenzprodukt MP (marginal product) gibt an, um wie
viel der Output sich erhöht, wenn der Einsatz eines Produktionsfaktors marginal erhöht wird.
MP 
y f (a  a, b)  f (a, b)

a
a
;
y y

 MP
a 0 a
a
lim
Typischerweise ist das Grenzprodukt abnehmend.
Die Grenzrate der technischen Substitution (GRtS) gibt an, auf wie viel vom Einsatzfaktor B man in der
Produktion einer bestimmten Outputmenge y verzichten kann, wenn man zusätzlich eine marginale
Mengeneinheit vom Einsatzfaktor A einsetzt.
Grafisch entspricht die Grenzrate der technischen Substitution dem Betrag der Steigung der Isoquanten bei
einer bestimmten Inputkombination (a,b):
Der Betrag der Steigung der Tangente an die Isoquante im Punkt (a,b) drückt die Grenzrate der technischen
Substitution i diesem Punkte aus: Der Betrag der Steigung bestimmt sich durch den Tangens von  :
Betrag der Steigung 
b
a
 GRtS
bzw.
GRtS  tan  
Gegenkathete b

Ankathete
a
Rechnerisch erhält man die Steigung und damit die Grenzrate der technischen Substitution wie folgt: Für alle
Inputkombinationen auf der Isoquanten gilt: y (a, b)  y . Das totale Differential der Isoquanten muss damit 0
sein, weil sich auf der Isoquanten ihr Wert nicht ändert: dy (a, b)  0 .
y
y
y
y
db
db
db MPA
a  
dy 
 da   db  0



GRtS  a 

y
y
a
b
da da
da MPB
b
b
44
Die Produktivität (AP: average productivity) eines Faktors A ist als das Durchschnittsprodukt des Faktors
y
A definiert: APA 
a
Eng mit dem Durchschnittsprodukt und dem Grenzprodukt verbunden ist die Produktionselastizität eines
Faktors A. Sie gibt an, um wie viel Prozent der Output Y wächst, wenn 1% mehr vom Faktor A eingesetzt wird:
y
MPA
y a
y
 y ,a 



a a y
APA
a
Ein weiteres Charakteristikum einer Produktionsfunktion ist ihr Homogenitätsgrad h. Eine Funktion ist
homogen vom Grade h falls gilt:
f (  a,   b)  h  f (a, b)
Der Homogenitätsgrad h gibt an, ob es sich um eine Produktionsfunktion mit fallenden, konstanten oder
steigenden Skalenerträgen SE handelt. Fallende Skalenerträge bedeuten, dass wenn von allen Faktoren
(Inputs) die doppelte Menge eingesetzt wird, der Output sich um weniger als das Doppelte vergrößert. Ein
Grund dafür können beispielsweise Organisationsschwierigkeiten sein, die mit steigender Größe auftreten.
Steigende Skalenerträge bedeuten, dass der Output um mehr als das doppelte zunimmt, wenn sämtliche
Faktoren verdoppelt werden. Mögliche Ursachen können Lerneffekte sein. Meist wird aber davon ausgegangen,
dass konstante Skalenerträge vorliegen, sich der Output also verdoppelt, wenn die Einsatzfaktoren alle
verdoppelt werden. Ein Homogenitätsgrad h bedeutet:

h=1
konstante Skalenerträge

h<1
fallende Skalenerträge

h>1
steigende Skalenerträge
Ist der Homogenitätsgrad h bei unterschiedlichen Werten von  konstant, so heißt die Produktionsfunktion
homogen, ist der Homogenitätsgrad h bei unterschiedlichen Werten von  nicht konstant, so heißt die
Produktionsfunktion inhomogen.
Beträgt der Homogenitätsgrad h gleich 1, liegen also konstante Skalenerträge vor, so heißt die
Produktionsfunktion linear.
1.2 Die Cobb-Douglas-Produktionsfunktion
Eine Produktionsfunktion der Form y(a, b)  a   b  heißt Cobb-Douglas-Produktionsfunktion.
Eine Produktionsfunktion der Form y(a, b)  a   b  mit     1 heißt linear-homogene C-D-P
2. Die Minimalkostenkombination
Der Produzent kennt nun seine Produktionsfunktion, repräsentiert durch Isoquanten. Wenn er eine bestimmte
Menge y produzieren möchte, hat er die Wahl zwischen vielen verschiedenen Inputfaktorkombinationen, mit
denen er die gewünschte Menge von Y produzieren kann. Der Produzent sei Preisnehmer, d.h. er kann die
Preise für die Inputfaktoren nicht beeinflussen. Die Preise für die Inputfaktoren A und B seien p a und p b .
Dann kostet die Beschaffung der Faktoren:
K  p a  a  pb  b
Sofern nichts anderes gesagt ist, schreiben wir auch für unbeeinflussbare Preise p a und p b .
Das Kostenniveau wird grafisch durch die Isokostenlinie repräsentiert.
Die Isokostenlinie ist der geometrische Ort aller Faktorkombinationen (a,b), die bei gegebenen Preisen p a und
p b die gleichen Kosten verursachen.
p
K
Bestimmungsgleichung:
K  p a  p b

b
 a a
a
b
pb

pb

OrdinatenabschnittSteigung
45
Das Auswahlproblem des Produzenten lässt sich grafisch nun lösen, indem man zunächst die Isoquante ein ein
a-b-Diagramm einzeichnet. Dann zeichnet man eine Isokostenlinie ein und verschiebt diese solange parallel, bis
sich die Isoquante und die Isokostenlinie gerade berühren. Der gefundene Punkt entspricht der
Minimalkostenkombination.
Die Minimalkostenkombination läst sich auch rechnerisch mit Hilfe des Lagrange-Ansatzes herleiten:
min K  p a  a  pb  b
a ,b
u.d.N . y  y  y (a, b)
L(a, b,  )  p a  a  pb  b    ( y (a, b)  y )
L
y (a, b) !

y (a, b)
 pa   
 0 
p

a
a
a
 a
 
!
L
y (a, b)
pb y (a, b)
Bedingungen 1. Ordnung: (2)
 pb   
 0 

b
b
b

!
L
(3)
 y ( a, b)  y  0

Ökonomische effizient wird produziert, wenn mit der Minimalkostenkombination produziert wird. Wird
ökonomische Effizient produziert, so auch technisch effizient. Die Umkehrung gilt nicht. Technische Effizienz
ist eine notwendige Bedingung für ökonomische Effizienz.
Aus diesem Ansatz lässt sich nun zweierlei herleiten:
Zum einen die bedingte Nachfrage nach den Produktionsfaktoren. Sie gibt an, wie viel das Unternehmen in
Abhängigkeit der Faktorpreise p a und p b und der Produktionsmenge y von vom jeweiligen Produktionsfaktor
nachfragt:
Dafür müssen wir an dieser Stelle die Produktionsfunktion konkretisieren, z.B.
pa b
p
y
y
y(a, b)  a  b

 b und
 a ; somit

 b*  a  a
a
b
pb a
pb
(1)
pa
pb
pa
 a  a* 
 y analog: b* 
y
pb
pa
pb
Zum anderen lässt sich die Kostenfunktion herleiten. Die Kostenfunktion gibt die minimalen Gesamtkosten
für die Produktion von y an:
Hierfür werden die Terme der bedingten Nachfrage einfach in die Kostengleichung K eingesetzt:
 pb

pa
pb
pa
K ( y )  K (a*, b*)  K 
 y;
 y   pa 
 y  pb 
 y  2  p a  pb  y
 p

pb
pa
pb
a


damit folgt: y  a  b 
y  a
3. Die Kostenfunktion
Die Kostenfunktion gibt also die minimalen Gesamtkosten für die Produktion der Menge y an. Bei der
Herleitung der Kostenfunktion ist es sehr wichtig, sämtliche Kosten zu erfassen, so auch die
Opportunitätskosten: entgangener Profit aus der zweitbesten Alternative. Dazu gehören der kalkulatorische
Unternehmerlohn sowie die kalkulatorischen Zinsen auf eigenes Kapital oder die entgangene Miete, dadurch,
dass die Räume selber benützt werden.
Um die richtigen Entscheidungen (Preisgestaltung der Produkte, Entscheidung über Marktein- oder -austritt
treffen zu können), müssen außerdem verschiedene Kostenarten unterschieden werden:
Variable Kosten (VC oder VK oder Kvar) sind Kosten, die sich bei Änderungen des Produktionsniveaus
ändern. Sie sind also direkt abhängig von der produzierten Menge.

Fixkosten (FC oder FK oder Kfix) sind Kosten, die sich bei Änderungen des Produktionsniveaus nicht
ändern. Sie fallen also an, egal ob und wie viel produziert wird. Sie können nur dadurch vermieden
werden, dass das Unternehmen das Geschäft aufgibt. (Gehälter leitender Führungskräfte, Mieten für
Werkshallen)
46


Quasifixe Kosten sind Kosten, die nicht anfallen, wenn nichts produziert wird, die aber, sobald auch nur
eine Mengeneinheit produziert wird, in von der Produktionsmenge unabhängiger Höhe anfallen.
(Beleuchtungskosten)
Versunkene Kosten (sunk costs) sind Kosten, die nicht rückholbar sind. Das sind beispielsweise die
Aufwendungen für eine Marketingkampagne, Investitionen für Spezialmaschinen, die nicht wieder
verkauft werden können oder Aufwendungen für Forschung, sofern die Forschungsergebnisse nicht
anderweitig vermarktet werden können. Sunk costs sind entscheidungsunrelevant.
Variable
Kosten
Quasifixe
Kosten
Fixe Kosten
Sunk costs
Rohstoffe,
Halbfertigfabrikate
Beleuchtung
Miete der Werkshalle,
Gehälter
Marketingaufwendungen
Spezialmaschinen
Kurze Frist
relevant
Mittlere Frist
relevant
Lange Frist
relevant
unrelevant
relevant
relevant
unrelevant
unrelevant
relevant
unrelevant
unrelevant
unrelevant
In den Kostenfunktionen innerhalb dieses Kurses werden nur die variablen und die fixen Kosten berücksichtigt.
Die Kostenfunktionen haben daher folgende Form:
K ( y )  FK  VK ( y )
Grenzkosten (MC, marginal costs) geben die Erhöhung der Kosten an, die sich ergibt, wenn eine (marginale)
Einheit mehr vom Output erzeugt wird.
K ( y ) VK ( y )
(die Ableitung der Fixkosten nach y ist 0)
MC 

y
y
Da die Grenzkosten gerade die Mehrkosten für eine weitere Einheit von Y umfassen, möchte der Produzent
mindestens einen Preis in Höher der Grenzkoten erzielen. Andererseits würde er beim Absatz der zuletzt
produzierten Mengeneinheit von Y einen Verlust erzielen.
Die durchschnittlichen Gesamtkosten (ATC average total costs, ØK) geben an, wie viel eine produzierte
Mengeneinheit durchschnittlich kostet.
K ( y ) FK VK
ATC  ØK 


y
y
y
Da die Fixkosten von der Ausbringungsmenge unabhängig sind, werden die durchschnittlichen Fixkosten pro
Stück umso geringer, je mehr produziert wird. Dieser Effekt wird auch als Fixkostendegression bezeichnet.
Wenn ein Unternehmer entscheidet, welchen Preis er langfristig verlangt, so wird er ihn mindestens in der Höhe
der durchschnittlichen Gesamtkosten ansetzen. Würde er weniger verlangen, so würde er einen Verlust erzielen.
Fixkostendegression:
Die durchschnittlichen variablen Kosten (AVC, average variable costs, ØVK) geben an, wie viel die
durchschnittlich (pro produzierter Einheit) die von der Produktionsmenge abhängigen Faktoren kosten.
VK(y)
AVC  ØVK 
y
Wenn ein Unternehmer entscheidet, welchen Preis er für eine weitere produzierte Einheit erzielen möchte, so
wird er einen Preis mindestens in Höhe der ØVK wählen, damit zumindest die Kosten für die Rohstoffe und
Halbfertigfabrikate und die Energie etc., die notwendig waren, um diese Einheit zu produzieren, gedeckt sind.
Die durchschnittlichen variablen Kosten werden mit steigender Produktionsmenge infolge der Knappheit als
steigend angenommen. [Wenn immer mehr Aluminium eingesetzt wird, dann steigt der Marktpreis für
Aluminium. Dann werden die Aluminiumproduzenten immer neue Aluminiumvorkommen erschließen, auch
solche, die bislang als unrentabel galten, dadurch steigt der Aluminiumproduktionspreis.]
47
3.1 Der Zusammenhang zwischen Durchschnittskosten und Grenzkosten
'
f
f ' g  fg '
Quotientenregel:   
g2
g
ØK 
K(y)
y
 K ( y )  dK ( y )

d 
 y  K ( y) 1
y 
dØK
1  dK ( y ) K ( y )  1
dy

   MC  ØK 


  

2
dy
dy
y  dy
y  y
y
3.2 Kurzfristige und langfristige Kosten
Langfristige könne alle Einsatzfaktoren optimal gewählt werden, während in der kurzen Frist einige
Einsatzfaktoren als gegeben angenommen werden (z.B. Fabrikgröße, Maschinenbestand).
Die Funktion, die jedem Output die minimalen Kosten zuordnet, wird als langfristige Kostenfunktion
bezeichnet.
Die Funktion, die jedem Output die minimalen Kosten bei einigen gegebenen Einsatzfaktoren zuordnet, wird
als kurzfristige Kostenfunktion bezeichnet.
Das Minimum der kurzfristigen Durchschnittskosten liegt in der Regel oberhalb der langfristigen
Durchschnittskosten.
3.3 Weitere Einflüsse auf die Kostenfunktion
Größenvorteile (economics of scale): Wenn der Output verdoppelt wird, erhöhen sich die Gesamtkosten um
weniger als das Doppelte. Größenvorteile können auf Skaleneffekten beruhen, aber auch darauf, dass bei einer
Zunahme der Größe unter Umstanden andere Einsatzfaktoren benützt werden (Substitution regional durch
überregional beziehbarer Stoffe; Substitution von Handarbeit durch Maschinen).
Ein Maß für die Höhe der Größenvorteile ist die Kosten-Output-Elastizität  K , y :
 K,y
K
K y MC
 K 
 
y
y K AC
y
Grenzkosten


 Durchschni ttskosten
Sie gibt an, um wie viel Prozent sich die Gesamtkosten ändern, wenn der Output um 1% erhöht wird.
Ist  K , y größer als 1, so liegen Größennachteile (diseconomies of scale) vor. Gründe dafür können
Organisationsprobleme sein oder Qualitätsprobleme durch die Zunahe des Produktionsniveaus (bei sehr
spezialisierten Handwerks- und Künstlerarbeiten).
Verbundvorteile (economies of scope) liegen vor, unterschiedliche Produkte besser von einem
Mehrproduktunternehmen gefertigt werden können als wenn die Produkte jeweils separat in einem
Einproduktunternehmen hergestellt werden (Weiterverarbeitung von Kuppelprodukten, Transportbranche:
Vermeidung von Leerfahrten durch Kombination von Gesamtladungen und Teilladungen). Ein Maß für
K ( y1 )  K ( y 2 )  K ( y1 , y 2 )
Verbundvorteile ist folgender Quotient: Grad der Verbundvorteile 
K ( y1 , y 2 )
Falls sich die Produktion der beiden Güter aber gegenseitig negativ beeinflusst (negative externe Effekte), so
liegen Verbundnachteile (diseconomies of scale) vor und die Kosten sind im Einproduktunternehmen
geringer als im Mehrproduktunternehmen.
Lernkurveneffekte liegen dann vor, wenn die Durchschnittskosten dadurch sinken, dass

Arbeitskräfte ihre Tätigkeiten im Laufe der Zeit immer schneller ausführen können (Einarbeitung,
Routine),

Führungskräfte lernen, den Produktionsprozess effektiver zu planen (bessere Kenntnis des
Produktionsprozesses im Laufe der Zeit),

Ingenieure Erfahrung mit dem Produkt sammeln, Toleranzen und Materialeigenschaften besser
einschätzen können,

Zulieferer lernen, die bestellten Teile effizienter zu verarbeiten
48
4. Das Angebot des Produzenten bei vollkommener Konkurrenz
Bei vollkommener Konkurrenz ist für die Produzenten sind die Marktpreise der von ihnen eingesetzten
Faktoren ( p a , p b ) sowie der von ihnen hergestellten Produkte ( p y ) gegeben. Sie sind Preisnehmer, also
Mengenanpasser.
Der Gewinn G(y) (in der Literatur auch Profit  ( y ) ) des Produzenten ergibt sich als Differenz von Umsatz
U(y) und Kosten K(y)
Maximierung des Gewinns (beeinflussbar: y; nicht beeinflussbar: die Preise)
G( y)  U ( y)  K ( y)  p y  y  K ( y)
max G ( y )  p y  y  K ( y )
y
Bedingung erster Ordnung:
dG ( y ) dU ( y ) dK ( y )


dy
d ( y)
dy
!
 0

dU ( y ) dK ( y )

d ( y)
dy
 
Grenzumsatz
dG ( y )

dy
py 
dK ( y )
dy
!
 0

py 
bzw.
Grenzkosten
dK ( y )
dy

Grenzkosten
Bedingung zweiter Ordnung:
d 2 G( y) !
0
dy 2
mit
d 2 G( y)
d 2 ( K ( y)


dy 2
dy 2
Ein Produzent wird also diejenige Menge von Y herstellen und absetzen, bei der für die letzte produzierte
Einheit gilt: Grenzumsatz = Grenzkosten
bzw.
Preis = Grenzkosten
Der gewinnmaximierende Produzent beachtet noch zwei weitere Einschränkungen:

Kurzfristig muss er mindestens seine variablen Kosten decken. Er bietet daher nur oberhalb der
durchschnittlichen variablen Kosten an.

Langfristig muss er auch die fixen Kosten decken. Er bietet daher nur oberhalb der durchschnittlichen
Gesamtkosten an.
Da langfristig sämtliche Faktoren variabel sind, verläuft die langfristige realiter flacher als die kurzfristige.
Falls die langfristigen Durchschnittskosten konstant sind, so verläuft die langfristige Angebotskurve als
Parallele zur Abszisse.
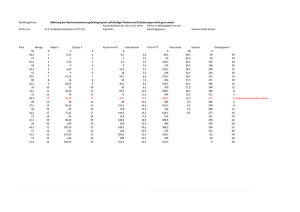
Unter der Produzentenrente (PR; oder ps: producer surplus) wird der Unterschied zwischen dem erzielten
Preis und der Abgabepreisuntergrenze (= Grenzkosten, MC) des Produzenten, kumuliert über alle abgesetzten
Mengeneinheiten verstanden. Kurzfristig entspricht die Produzentenrente also dem Umsatz abzüglich der
variablen Kosten, was dem Gewinn zuzüglich der Fixkosten gleichkommt.
PR( y )  U ( y )  VK ( y )  G ( y )  FK
Da langfristig alle Faktoren variable sind, entspricht die Produzentenrente langfristig dem langfristigen
ökonomischen Gewinn:
PR( y )  U ( y )  VK ( y )
Grafisch lässt sich die Produzentenrente auch als die Fläche zwischen dem Marktpreis und der
Grenzkostenkurve darstellen
49