Kondensatoren

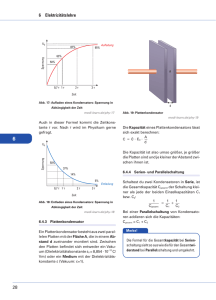
C. B.
Melanie Thompson
25.12.2005
Versuch 8 vom 5.Kurstag dem 06.12.2005:
Auf- und Entladung eines Kondensators, einfaches RC-Netzwerk
Einleitung
Ein Kondensator ist ein elektrisches Bauelement zur Speicherung von Energie in einem
elektrischen Feld.
Zumeist bilden zwei gegeneinander isolierte leitende Flächen beliebiger Größe und
Krümmung einen Kondensator, im einfachsten Fall sind es zwei einander parallel im Abstand
d gegenüberstehende Metallplatten mit der Fläche A.
Die Platten können nun mit jeweils einem Pol einer Spannungsquelle verbunden werden, was
zur Folge hat, dass mit der Zeit exponentiell abnehmender elektrischer Strom fließt.
Bei diesem Vorgang wird eine Platte positiv, die andere negativ aufgeladen, diese Ladung
bleibt erhalten, auch wenn man den Kondensator von der Stromquelle trennt.
Will man den Kondensator entladen verbindet man beide Platten, woraufhin so lang Strom
fließt, bis die Ladungen der Platten ausgeglichen und sie damit neutral sind.
Kondensatoren bieten also die Möglichkeit einer kurzfristigen reversiblen
Ladungsspeicherung.
Die gespeicherte Ladung Q ist proportional zur angelegten Spannung U
U C  Q
oder
´
Q
C
U
, will heißen je höher die Spannung ist, desto mehr Ladung kann gespeichert werden,
C
abhängig ist dieser Proportionalitätsfaktor – die Kapazität C (Einheit 1F  1 ) - von der
V
Bauart des Kondensators.
Die Kapazität C beschreibt damit die Fähigkeit eines Körpers, Ladungen zu speichern, diese
muss bei Kondensatoren geeignet hoch sein, damit die Kondensatoren wirklich effektiv
Ladung speichern.
Die Kapazität eines Kondensators hängt von der Größe der Platten, ihrem Abstand zueinander
und dem Material zwischen den Platten (dem sog. Dielektrikum) ab.
Somit ergibt sich für die Kapazität C des Plattenkondensators:
C   0
A
d
Dabei ist  0 = 8,8542.10-12 As/Vm die elektrische Feldkonstante und,  die (relative)
Dielektrizitätskonstante des Mediums zwischen den Platten.
In einem Schaltkreis können Kondensatoren auch in Reihe oder parallel geschaltet werden,
die Gesamtkapazität wird dann wie folgt berechnet:
Parallelschaltung:
CGesamt  C1  C 2  ...
Reihenschaltung:
1

C Gesamt
1
1

 ...
C1 C 2
Schaltet man bei Gleichspannung einen entladenen Kondensator mit einem Ohmschen
Widerstand in Reihe, so lädt sich der Kondensator auf.
Es fließt so lang Strom, bis die Spannung UC am Kondensator gleich der angelegten
Spannung U0 ist.
Der Ladungsstrom I und die angelegte Spannung hängen durch eine e-Funktion von der Zeit
wie folgt ab:
t
U C (t )  U 0 (1  e RC )
bzw. :
U0
I (t ) 
t
R  e RC
Für die Aufladung des Kondensators gilt analog:
U C (t )  U 0  e
t
RC
und
U C (t ) 
U0
t
R  e RC
RC wird auch als Zeitkonstante  des Netzwerkes beschrieben, sie stellt die Zeit dar, in der
Strom und Spannung eines Netzwerkes auf ihren e-ten Teil abgefallen sind.
Bestimmt man diese Zeitkonstante , so kann man bei bekanntem Widerstand ohne Probleme
die Kapazität C eines Kondensators bestimmen:
RC  
bzw.
C

R
Aufbau und Durchführung
Die in diesem Versuch verwendeten Kondensatoren sind sog. Metall-Papier-Kondensatoren,
bestehend aus zwei dünnen Metallfolien, die durch eine dünne Schicht isolierendes Papier (?)
getrennt und damit aufgewickelt werden.
Der Aufbau der Schaltung sieht wie folgt aus:
Mit Hilfe eines Zweikanal- oder SEVOREC-Schreibers wird die Kapazität der Kondensatoren
wie folgt ermittelt:
Auf den entstandenen Kurven nimmt man zunächst den maximalen Ausschlag und berechnet
anhand der auf dem Papier vorhandenen Kästchen (1Kästchen = 20mA) den mA-Bereich, den
dieser Ausschlag umfasst.
Den hier erhaltenen Wert teilt man durch e, um den e-ten Teil zu erlangen, der dann auf der
fortlaufenden Kurve aufgetragen wird.
Der hier erhaltene Punkt wird mit dem Messpunkt des maximalen Ausschlags verbunden und
der Abstand in mm kann anhand der Fortlaufgeschwindigkeit des Schreibers ohne weiteres in
Sekunden umgerechnet werden.
Diesen Wert  teilt man nun, wie in obiger Formel beschrieben, durch den verwendeten
Widerstand und erhält so die Kapazität C des Kondensators.
Aufgaben
1. Bestimmung der Kapazitäten der Kondensatoren nach oben genannter Messmethode
2. Bestimmung der Kapazitäten der Kondensatoren in Reihen- und Parallelschaltung,
Vergleich der in Aufgabe 1 ermittelten Werte
3. Herleitung folgender Gleichungen:
a) CGesamt  C1  C 2  ... für die Parallelschaltung
1
1
1


 ... für die Reihenschaltung
b)
C Gesamt C1 C 2
Ergebnisse
1.
Kondensator C1
Aufladen
Entladen
Mittelwert
 [s]
10,75s
11s
C [F]
106,9
109,3
108,1
Kondensator C2
Aufladen
Entladen
Mittelwert
 [s]
11s
10,75s
C [F]
109,3
106,9
108,1
2.
Die experimentell in der ersten Aufgabe ermittelten Werte können nun verwendet werden um
rechnerisch die in Aufgabe 2. erwarteten Werte zu erlangen.
In Reihenschaltung lauten die theoretisch ermittelten Werte wie folgt:
CGesamt 
(C1  C 2 )
 54,05F
(C1  C 2 )
Parallel geschaltet würde sich für die Kondensatoren eine theoretische Kapazität wie folgt
ergeben:
CGesamt  C1  C 2  216,2F
Experimentell wurden folgende Werte ermittelt:
C1 und C2 in Reihe
Aufladen
Entladen
Mittelwert
 [s]
5,5s
5,5s
C [F]
54,7
54,7
54,7
C1 und C2 parallel geschaltet
Aufladen
Entladen
Mittelwert
 [s]
21,5s
21,25s
C [F]
214
211
212,5
Wie man erkennen kann, weichen die rechnerisch ermittelten Werte nicht stark von den
experimentell ermittelten Werten ab.
Die bestehenden Abweichungen lassen sich über Messfehler erklären.
3.
Die Gleichungen für die Parallel- und die Reihenschaltung leiten sich wie folgt her:
Bei der Parallelschaltung liegt die gleiche Spannung U an den Kondensatoren an, darum gilt:
Q1  C1  U
und
Q2  C 2  U
woraus folgt:
Q1  Q2  (C1  C2 )  U
Die Gesamtladung entspricht also der Summe aller Einzelladungen, woraus sich für die
Parallelschaltung folgende Kapazität ergibt:
CGesamt  C1  C2
Und folgende Gesamtladung gespeichert werden kann:
QGesamt  Q1  Q2
Bei der Reihenschaltung ist die Gesamtspannung U die Summe der Einzelspannungen U1 und
U2, jeder Kondensator enthält die gleiche Ladung Q, woraus folgt:
Q
 U1
C1
und
Q
 U2
C2
Durch U = U1 + U2 ergibt sich dann:
 1   1
U  Q    
 C1   C 2

Q
 
 C Gesamt
Womit sich für die Reihenschaltung folgende Formel ergibt:
1
C Gesamt

1
1

C1 C 2
oder
C Gesamt 
(C1  C 2 )
(C1  C 2 )
Fehlerrechnung
Mögliche Fehlerquellen in diesem Versuch sind:



Fehler beim Erstellen und Auswerten der Graphen
Ungenaues Einstellen des Schreibers und seines Nullpunktes
Ungenaues betätigen der Taster
Die für die Fehlerrechnung genutzte Formel lautet wie folgt:
C  R


C

R
bzw.
  R 
C  

C
R 
 
Es wird von folgenden Fehlern ausgegangen:
  1s
R
 0,02
R
Damit ergeben sich folgende Fehler für die Messungen:
Kondensator/Schaltung
 [s]
C [F]
C1 (aufladen)
C1 (entladen)
C2 (aufladen)
C2 (entladen)
C1 + C2 in Reihe
(aufladen)
C1 + C2 in Reihe
(entladen)
C1 + C2 parallel
(aufladen)
C1 + C2 parallel
(entladen)
10,75
11
11
10,75
5,5
106,9
109,3
109,3
106,9
54,7
Absoluter Fehler
[F]
12,08
12,12
12,08
12,12
11,04
Prozentualer
Fehler[%]
11,3
11,1
11,1
11,3
20,2
5,5
54,7
11,04
20,2
21,5
214
14,23
6,7
21,25
211
14,15
6,7