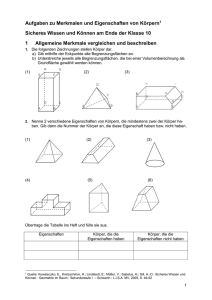
mathbu.ch 9 Aufgabensammlung 6 Pyramide und Prisma 1) Körper

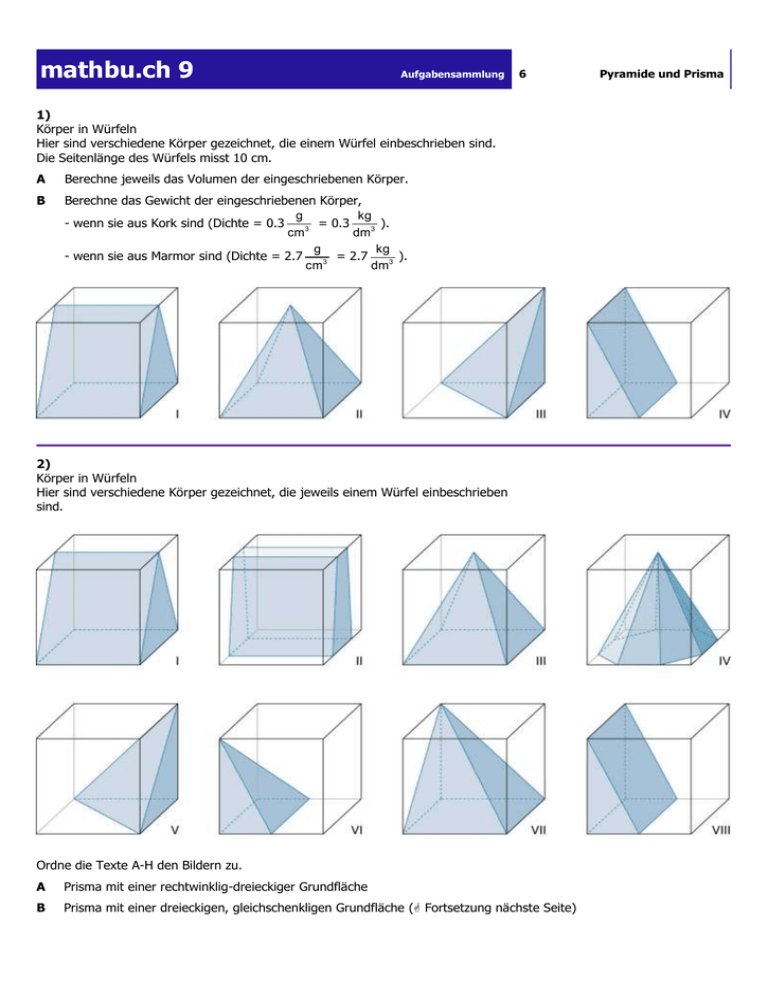
mathbu.ch 9
Aufgabensammlung
6
1)
Körper in Würfeln
Hier sind verschiedene Körper gezeichnet, die einem Würfel einbeschrieben sind.
Die Seitenlänge des Würfels misst 10 cm.
A
Berechne jeweils das Volumen der eingeschriebenen Körper.
B
Berechne das Gewicht der eingeschriebenen Körper,
g
kg
- wenn sie aus Kork sind (Dichte = 0.3
= 0.3
).
3
cm
dm3
g
kg
- wenn sie aus Marmor sind (Dichte = 2.7
= 2.7
).
3
cm
dm3
2)
Körper in Würfeln
Hier sind verschiedene Körper gezeichnet, die jeweils einem Würfel einbeschrieben
sind.
Ordne die Texte A-H den Bildern zu.
A
Prisma mit einer rechtwinklig-dreieckiger Grundfläche
B
Prisma mit einer dreieckigen, gleichschenkligen Grundfläche ( Fortsetzung nächste Seite)
Pyramide und Prisma
mathbu.ch 9
Aufgabensammlung
C
gerade quadratische Pyramide
D
gerade Pyramide mit einer regelmässigen achteckigen Grundfläche
E
schiefe Pyramide mit rechtwinklig-gleichschenkliger Grundfläche
F
schiefe quadratische Pyramide
G
schiefe Pyramide mit rechteckiger Grundfläche
H
Prisma mit einer trapezförmigen, gleichschenkligen Grundfläche
3)
Pyramide herstellen und berechnen
A
Zeichne die Abwicklung einer geraden Pyramide, deren Grundfläche
quadratisch ist (a = 5 cm). Die Pyramide ist 7 cm hoch.
B
Berechne die Mantelfläche, die Grundfläche und das Volumen.
4)
Körper in Würfeln
Die Namen der Körper lauten:
- Quader
- Prisma mit einer dreieckigen, gleichschenkligen Grundfläche
- Prisma mit einer rechtwinklig-dreieckigen Grundfläche
- gerade quadratische Pyramide
A
Ordne die Texte den Bildern zu. Färbe jeweils die Grundfläche.
B
Erstelle eine Reihenfolge vom Körper mit dem grössten Volumen bis zum
Körper mit dem kleinsten Volumen.
6
Pyramide und Prisma
mathbu.ch 9
Aufgabensammlung
5)
Schneidet man die Pyramide auf halber Höhe parallel zur Standfläche durch, und
schneidet man anschliessend aus dem verbleibenden Stumpf mit geraden Schnitten
(wie skizziert) einen Würfel aus, so entstehen insgesamt 5 Teilkörper. Die beiden
kleinen Pyramiden sind gleich gross.
A
Bezeichne die fünf Teilkörper.
B
Wie gross ist das Volumen der grossen Pyramide im Vergleich zum „StartWürfel"?
C
Berechne je das Volumen der 5 Teilkörper, wenn die Seite des „Start-Würfels“
20 cm misst.
6
Pyramide und Prisma
mathbu.ch 9
Aufgabensammlung
6)
Eine Pyramide wird aus einem Würfel geschnitten. Die Würfelseite misst 20 cm.
Berechne das Volumen des Abfalls,
A
wenn die Pyramidenspitze in einer Ecke des Würfels liegt.
B
wenn die Pyramidenspitze in der Mitte der Deckfläche liegt.
7)
Pyramide berechnen (Bild von Nr. 6)
Die Seitenlänge des Würfels misst 6 cm.
A
Zeichne den Mantel dieser Pyramide.
B
Berechne die Mantelfläche.
8)
Pyramide berechnen (Bild von Nr. 6)
Die Seitenlänge des Würfels misst 6 cm.
Berechne das Volumen der Pyramide.
9)
Pyramide mit achteckiger Grundfläche
Die Pyramide ist 10 m hoch. a misst 2 m, d misst 5.2 m und e misst 4.8 m.
Berechne das Volumen der Pyramide.
6
Pyramide und Prisma
mathbu.ch 9
10)
Pyramidenvolumen anhand der Grundfläche berechnen
Alle Pyramiden sind je 10 m hoch. a = 7 cm, ha = 6 cm.
Berechne das Volumen der Pyramiden.
Grundfläche der Pyramide A:
Grundfläche der Pyramide B:
a
Grundfläche der Pyramide C:
Aufgabensammlung
6
Pyramide und Prisma