1 Grundwissen Pyramide

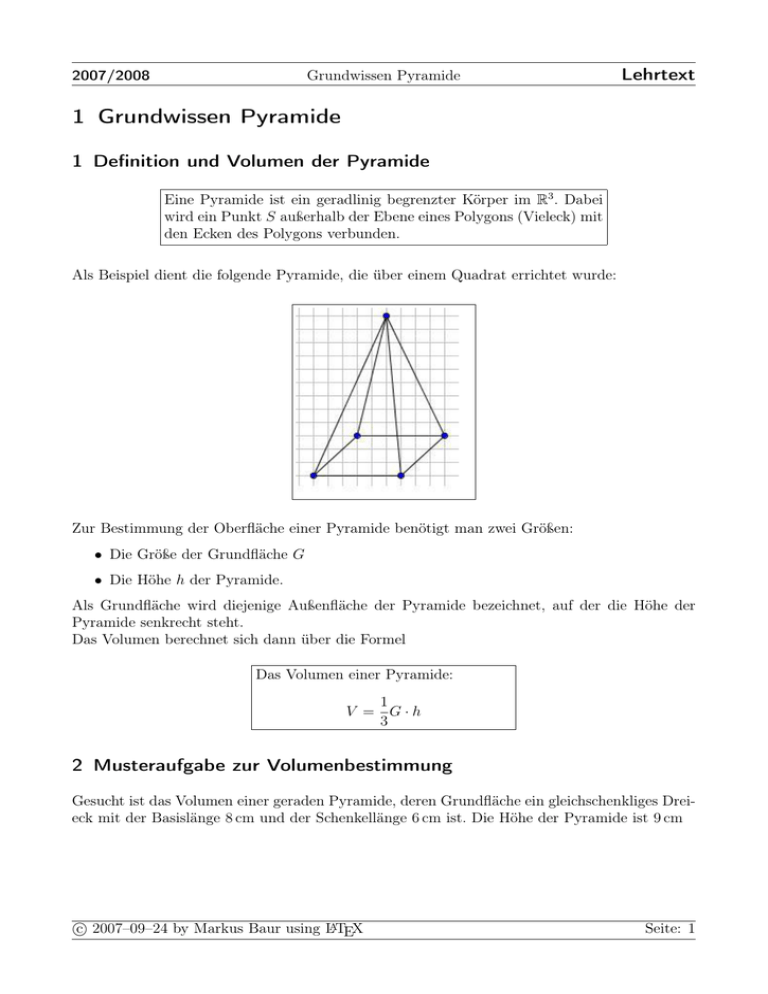
2007/2008
Grundwissen Pyramide
Lehrtext
1 Grundwissen Pyramide
1 Definition und Volumen der Pyramide
Eine Pyramide ist ein geradlinig begrenzter Körper im R3 . Dabei
wird ein Punkt S außerhalb der Ebene eines Polygons (Vieleck) mit
den Ecken des Polygons verbunden.
Als Beispiel dient die folgende Pyramide, die über einem Quadrat errichtet wurde:
Zur Bestimmung der Oberfläche einer Pyramide benötigt man zwei Größen:
• Die Größe der Grundfläche G
• Die Höhe h der Pyramide.
Als Grundfläche wird diejenige Außenfläche der Pyramide bezeichnet, auf der die Höhe der
Pyramide senkrecht steht.
Das Volumen berechnet sich dann über die Formel
Das Volumen einer Pyramide:
1
V = G·h
3
2 Musteraufgabe zur Volumenbestimmung
Gesucht ist das Volumen einer geraden Pyramide, deren Grundfläche ein gleichschenkliges Dreieck mit der Basislänge 8 cm und der Schenkellänge 6 cm ist. Die Höhe der Pyramide ist 9 cm
c 2007–09–24 by Markus Baur using LATEX
Seite: 1
2007/2008
Grundwissen Pyramide
Lehrtext
Lösung der Aufgabe
Die Lösung der Aufgabe zerfällt in zwei Arbeitsschritte:
• Schritt 1: Bestimmung des Flächeninhalt der Grundfläche
Zunächst muss man die Höhe des Dreiecks auf bestimmen, die auf der Basis senkrecht
steht.
Man setzt zur Lösung mit dem Hauptsatz des Pythagoras an:
c 2
2
= b2
hd +
2
h2d + (4 cm)2 = (6 cm)2
h2d + 16 cm2 = 36 cm2
h2d = 20 cm2
√
hd = 20 cm
hd = 4,47 cm
Damit kann man nun mit der Flächenformel für ein Dreieck den Flächeninhalt der Grundfläche bestimmen:
1
G = · 4,47 cm · 8 cm
2
G = 17,88 cm2
• Schritt 2: Anwendung der Volumenformel
V =
1
· 17,88 cm2 · 9 cm
3
V = 53,64 cm3
c 2007–09–24 by Markus Baur using LATEX
Seite: 2
2007/2008
Grundwissen Pyramide
Lehrtext
3 Das Netz einer Pyramide
Trennt man die Pyramide an den Kanten auf und klappt die Seitenflächen der Pyramide in die Ebene der Grundfläche, so entsteht
ein zweidimensionales Faltmodell der Pyramide. Dieses wird in der
Fachsprache als Netz einer Pyramide bezeichnet.
Beispiel
Konstruiere das Netz einer geraden Pyramide, deren Grundfläche ein reguläres 5- Eck ist mit
dem Umkreisradius 3 cm und die Höhe der Pyramide ist 6 cm
Konstruktive Lösung
Konstruktion des Netzes
c 2007–09–24 by Markus Baur using LATEX
Seite: 3
2007/2008
Grundwissen Pyramide
Lehrtext
Benötigte Hilfskonstruktion
Konstruktionsanleitung
1. Konstruiere das reguläre Fünfeck. Da es sich um eine gerade Pyramide handelt ist A der
Fußpunkt der Höhe. A ist gleichzeitig der Mittelpunkt der Grundfläche G.
2. Um das Netz konstruieren zu können benötigt man die Höhe der Seitenflächen. Diese kann
man in einer Hilfskonstruktion über den Satz des Pythagoras ermitteln:
a) Miss mit dem Zirkel den Abstand von A zu dem Mittelpunkt einer Seitenkante der
Grundfläche. Übertrage ihn auf eine waagrechte Gerade. Dadurch ergeben sich in der
Hilfsfigur die Punkte G und H.
b) Errichte das Lot l auf dem Punkt G.
c) Zeichne einen Kreis mit Mittelpunkt G und Radius r = 6 cm. Dadurch ergibt sich
der Punkt I.
d) Die gesuchte Höhe der Seitenfläche ist IH.
3. Errichte auf den Seitenkanten der Grundfläche G die Lot durch deren Mittelpunkt.
4. Zeichne um jeden Mittelpunkt einen Kreis mit Radius r = IH
c 2007–09–24 by Markus Baur using LATEX
Seite: 4
2007/2008
Lehrtext
Grundwissen Pyramide
4 Grundwissenaufgaben zur Pyramide
Aufgaben
Lösungen
Bei einer Pyramide wird die Kantenlänge der
quadratischen Grundfläche verdoppelt. Wie
Richtige Antwort: Das Volumen vervierfacht
ändert sich dabei das Volumen?
sich.
1. Das Volumen verdoppelt sich
2. Das Volumen verdreifacht sich
3. Das Volumen vervierfacht sich
Eine Pyramide hat eine Grundfläche eines
gleichseitigen Dreiecks mit der Seitenlänge
6 cm. Die Höhe beträgt 9 cm Berechne das
Volumen der Pyramide.
1. Berechnung der Grundfläche:
s 2
h2g = s2 −
2
s√
3
hg =
2
hg = 4,33 cm
1
G = shg
2
G = 10,825 cm2
2. Anwendung der Volumenformel
1
V = Gh
3
V = 30,75 cm3
Eine gleichseitige Pyramide hat eine quadratische Grundfläche mit der Kantenlänge
6 cm. Die Höhe der Pyramide ist 4 cm. Berechne die Oberfläche der Pyramide.
1. Berechne die Höhe eine Seitenfläche
über den Satz von Pythagoras:
s 2
2
2
hs = h +
2
√
hs = 32 + 42 = 5 cm
2. Berechnung einer Seitenfläche
1
As = ghs = 15 cm2
2
3. Berechnung der Oberfläche:
O = G + 4As
O = 36 cm2 + 4 · 15 cm2 = 96 cm2
c 2007–09–24 by Markus Baur using LATEX
Seite: 5