Hundekurve_Richtungsfelder_Evoluten_Affensattel

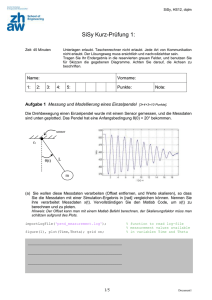
Aufgabenstellung „Hundekurve“:
Ein Herr steht auf einer Seite eines Flusses (im Ursprung eines x-y Koordinatensystems), der
Hund genau gegenüber am anderen Ufer (Koordinate (a,0), a ist die Breite des Flusses)..
Der Fluss fließt (überall mit konstanter) Geschwindigkeit c in y-Richtung.
Der Hund springt nun ins Wasser und schwimmt so, dass seine Schnauze immer
Auf den Herrn zeigt mit konstanter Geschwindigkeit v.
Unter welchen Voraussetzungen erreicht er den Herrn und wie lautet ggf. die Bahnkurve ?
Dazu stelle man eine geeignete Differentialgleichung auf und löse sie.
Man setzt vektoriell an den Geschwindigkeitsvektor des Hundes, dessen
Schnauze immer auf den Herrn zeigt:
v/sqrt(x*x+y*y) mal Vektor (-x,-y), v = Schwimmgeschwindigkeit des Hundes, als
konstant angenommen. Herr steht in (0,0),
Hund springt bei (a,0),a = Flussbreite) ins Wasser x Achse quer zum Fluss
.dazu Vektor (0,c= Geschwindigkeit des Wassers, überall gleich angenommen)
Dieser Vektor entspricht ypunkt/xpunkt.
Nachdem man t (Zeitparameter eliminiert hat und ypunkt/ xpunkt gebildet hat ergibt sich die
DGL: y' = (v*y-c*sqrt(x*x+y*y))/v*x .
y/x wird durch u substituiert, dann ergibt sich die DGL
u'*x = -c*sqrt(1+u*u)/v
Jetzt Trennung der Variablen und integrieren liefert
ln(u+sqrt(1+u*u) ) = -c/v ln(abs(x)) + Konstante
delogarithmieren, u nach rechts, quadrieren,
nach u auflösen und wieder u ersetzen durch y/x liefert
y = 1/2*K*x hoch (-c/v+1) - 1/(2*K) *x hoch (c/v+1) mit K Konstanter, die aus obiger
exponentiell hervorgeht beim Delogarithmieren.
Dann v<c keine Lösung, Hund wird abgetrieben, v=c Verharren in Endposition,
v>c Herr wird erreicht Anfangsbedingung y(0) = a (Reinspringpunkt des Hundes)
noch einarbeiten liefert Bedingung für die Konstante K = a hoch (c/v).
Plot der "Hundekurve" aus der Vorlesung mit Maple Version 9:
> restart;
> a:=10.0; # Breite des Flusses
> cdv := 0.8: #v = Schwinngeschwindigkeit Hund
c = Fliesgeschwindigkeit Fluss cdv = c/v deren Quotient .
> y:= a^cdv/2*x^(-cdv+1) -a^(-cdv)/2*x^(cdv+1);
> plot(y,x=0..10);
Zeichnen von Richtungsfeldern einer DGL (mit Maple 9)
Aus der Kreisgleichung x^2 + y^2 = r^2 folgt
y' = -x/y, DGL aller Kreise um den Ursprung.
> restart:
> with(DEtools):
> dfieldplot(diff(y(x),x) = -x/y(x), y(x), x=-3..3,
> y=-3..3,title=`y'= -x/y`);
DGL y' = y Lösung = K*exp(x)
> dfieldplot(diff(y(x),x) = y(x), y(x), x=-3..3,
> y=-3..3,title=`y'= y`);
Aufgabe zum Selbermachen:
Zeichen Sie das Richtungsfeld der DGL y' =y - y^2, diese DGL
wurde in der Vorlesung behandelt und das Richtungesfeld gezeichnet.
> dfieldplot(diff(y(x),x) = y - y(x)^2,y(x),x=-3..3,y=-3..3);
>
Warning, y is present as both a dependent variable and a name. Inconsistent
specification of the dependent variable is deprecated, and will be removed in
the next release.
Zeichnen mehrerer Lösungskurven einer DGL
> x := 'x':
> y := 'y':
> y - y^2:
> F
:= unapply(%,x,y); # F = rechte Seite der DGL als echte
Funktion
> dgl := diff(y(x),x)=F(x,y(x)): # die DGL
ermittle ALLGEMEINE LÖSUNG der DGL mit der MP dsolve
> dsolve(dgl,y(x));
> subs(_C1 = C,%);
# Lösungen explizit
# I-Konstante _C1 umbenennen in C
#Zeichnen einiger Lösungskurven aus der Schar:
> plot([seq(1/(1+C*exp(-x)),C=-1..1)],x=-1..3,y=-2..2);
>
Berechnung der Evolute für eine Ellipse:
> a := 5: # lange Halbachse der Ellipse
> b := 3: # kleine Halbachse der Ellipse
> x := a*cos(t);
> xpunkt := diff(x,t):
> x2punkt := diff(xpunkt,t):
> y := b*sin(t);
> ypunkt := diff(y,t):
> y2punkt := diff(ypunkt,t):
> nenner := xpunkt*y2punkt-ypunkt*x2punkt:
> bruch := (xpunkt^2+ypunkt^2)/nenner:
> xevo := x - ypunkt*bruch;
> yevo := y + xpunkt*bruch;
> plot([xevo(t),yevo(t),t=0..2*Pi],scaling = constrained);
> plot({[x(t),y(t),t=0..2*Pi],[xevo,yevo,t=0..2*Pi]});
Evolute der Normalparabel:
> x := 'x';
> y := x^2;
> ys := diff(y,x);
> yss := diff(y,x$2):
> bruch:= (1+ys^2)/yss;
> xevo := x - ys*bruch;
> xevo:=simplify(%);
> L:= solve(xwert-4*x^3=0,x):
> L[1];
> yevo := y + bruch;
> ywert:= subs(x=L[1],yevo);# Neilsche Parabel
> plot(y(x),x=-4..4);
> plot([xevo(x),yevo(x),x=-4..4],-4..4,-4..4);
> plot({[x,y(x),x=-4..4],[xevo(x),yevo(x),x=-4..4]},-2..2,0..4);
>
> plot({y(x),[xevo(x),yevo(x),x=-2..2]},x=-2..2);
Man gebe eine Gleichung yevo = f(xevo) der Neilschern Parabel an!
(Dazu ist die erste Gleichung nach x aufzulöen und in die zweite einzusetzen
Affensattel
> restart;
> z := 3*y*x^2-y^3;
>
> plot3d(z,x=-5..5,y=-5..5,title = 'Affensattel');