Übung 1: Signale und Systeme
Werbung
SiSy, HS12, dqtm
SiSy Kurz-Prüfung 1:
Zeit: 45 Minuten
Unterlagen erlaubt. Taschenrechner nicht erlaubt. Jede Art von Kommunikation
nicht erlaubt. Der Lösungsweg muss ersichtlich und nachvollziehbar sein.
Tragen Sie Ihr Endergebnis in die reservierten grauen Felder, und benutzen Sie
für Skizzen die gegebenen Diagramme. Achten Sie darauf, die Achsen zu
beschriften.
Name:
1:
2:
Vorname:
3:
4:
5:
Punkte:
Aufgabe 1 Messung und Modellierung eines Einzelpendel
Note:
[3+4+3=10 Punkte].
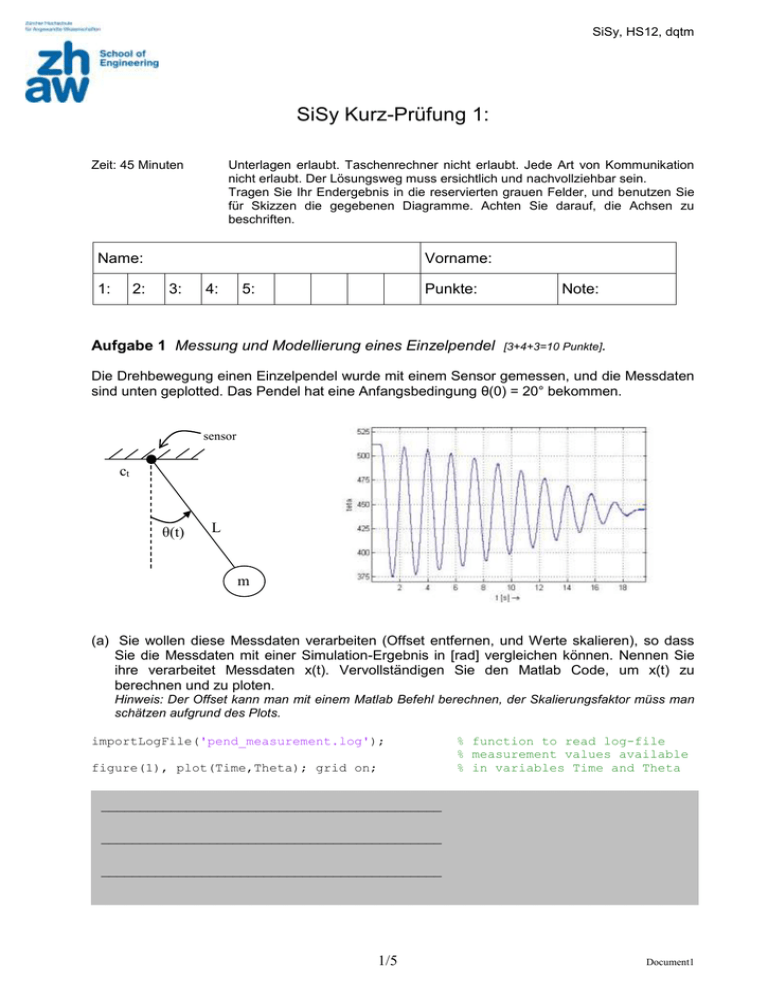
Die Drehbewegung einen Einzelpendel wurde mit einem Sensor gemessen, und die Messdaten
sind unten geplotted. Das Pendel hat eine Anfangsbedingung θ(0) = 20° bekommen.
sensor
ct
θ(t)
L
m
(a) Sie wollen diese Messdaten verarbeiten (Offset entfernen, und Werte skalieren), so dass
Sie die Messdaten mit einer Simulation-Ergebnis in [rad] vergleichen können. Nennen Sie
ihre verarbeitet Messdaten x(t). Vervollständigen Sie den Matlab Code, um x(t) zu
berechnen und zu ploten.
Hinweis: Der Offset kann man mit einem Matlab Befehl berechnen, der Skalierungsfaktor müss man
schätzen aufgrund des Plots.
importLogFile('pend_measurement.log');
figure(1), plot(Time,Theta); grid on;
% function to read log-file
% measurement values available
% in variables Time and Theta
K ____________________________________________
= pi/9/70;
% or similar value, in praxis read out
% factor after removing offset
x_t
=
K*(
Theta
-mean(Theta));
% Offset & Skalierung bearbeiten
____________________________________________
figure(2),plot(Time,x_t)
% Plot x_t
____________________________________________
1/5
Document1
SiSy, HS12, dqtm
(b) Bestimmen Sie die Differentialgleichung, welche die Drehbewegung θ(t) des Pendels
beschreibt. Berücksichtigen Sie den Effekt der Schwerkraft, und der Dämpfung ct.
Hinweis: Vereinfachen Sie ihre DGl mit der Klein-Winkel-Approximation.
DGL : ______________________________________
(c) Bereiten Sie eine Skizze des Blockschaltbildes, mit dem Sie eine Simulation der PendelBewegung in Simulink durchführen können. Vergessen Sie nicht zu kennzeichen, wo man
die Anfangsbedingung eingeben soll.
Aufgabe 2 Bodediagram
θ(t)
[5+5=10 Punkte].
Die Frequenz-Antwort (oder Frequenzgang) G(ω) von einem System ist unten gegeben:
G
10
;
j 1
mit 10 m s
Vervollständigen Sie die Tabelle unten und bereiten Sie eine Skizze des Bodediagrammes.
Vergessen Sie nicht die Achse zu beschriften.
Regions
G(ω) ≈ ……..
abs{G(jω)}
Phase{G(jω)}
ω << 1/τ
Asymptote:
ω = 1/τ
Punkt:
ω=10/ τ :
ω >> 1/τ
ω=100/ τ
Asymptote:
2/5
Document1
SiSy, HS12, dqtm
Aufgabe 3 System Beschreibungsarten
[3+2+3=8 Punkte].
Das Blockschaltbild von einem LTI System ist unten gegeben.
u(t)
A
+
+
1/C
y(t)
B
+
-
D
(a) Bestimmen Sie die Gleichung, welche y(t) gemäss das BSB beschreibt.
Gleichung : __________________________________
(b) Leiten Sie beide Seiten dieser Gleichung bezüglich t ab, um die Differentialgleichung von
System zu bekommen.
DGL : ______________________________________
3/5
Document1
SiSy, HS12, dqtm
(c) Bestimmen Sie die Übertragungsfunktion G(ω), welche dieses System beschreibt.
Benutzen Sie dafür Ihre Ergebnis (Differentialgleichung) von Teilaufgabe (b).
G(ω) : ___________________
Aufgabe 4 Faltung von kontinuierliche Zeitfunktionen [8 Punkte].
yt ut g t
Die Funktion y(t) wird berechnet durch Faltung von u(t) und g(t) :
Vervollständigen Sie in unteren Diagrammen die fehlenden Kurven. Begründen Sie ihre Antwort
mit der Berechnung des Faltungsintegrals bei den gefragten Zeitpunkten.
y t t 1 ?
y t t 0 ?
y t t 1 ?
4/5
Document1
SiSy, HS12, dqtm
Aufgabe 5 Diskretes System [4+4+2=10 Punkte].
Die Differenzengleichung eines diskreten System (LTD) wird unten gegeben:
yn 1 xn 2 xn 1 2 xn 2 1 xn 3
(a) Bereiten Sie eine Skizze der Impulsantwort des Systems.
(b) Vervollständigen Sie das untere Blockschaltbild des Systems.
y[n]
u[n]
(c) Mit welchem Faktor wurden Sie das Ausgangssignal y[n] skalieren, um einen
vergleichbaren Wertbereich für y[n] wie x[n] zu behalten? Begründen Sie ihre
Antwort mit einem kurzen Satz.
Faktor : ______________________________________
5/5
Document1