SiSy_HS12_sempruef_lsg

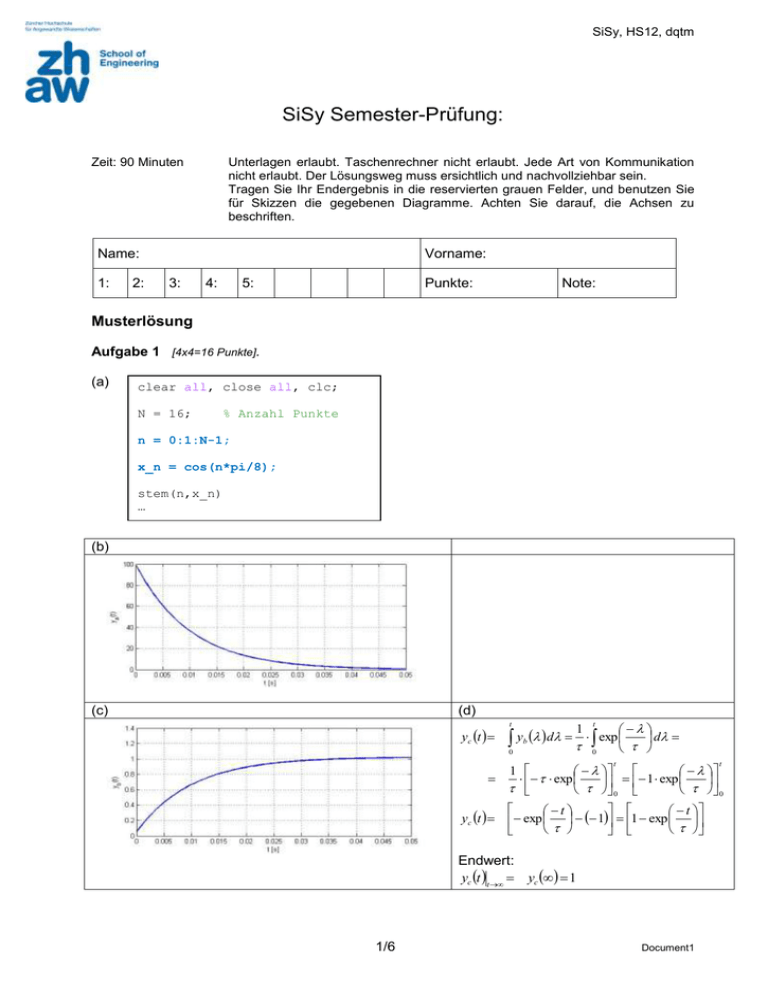
SiSy, HS12, dqtm
SiSy Semester-Prüfung:
Zeit: 90 Minuten
Unterlagen erlaubt. Taschenrechner nicht erlaubt. Jede Art von Kommunikation
nicht erlaubt. Der Lösungsweg muss ersichtlich und nachvollziehbar sein.
Tragen Sie Ihr Endergebnis in die reservierten grauen Felder, und benutzen Sie
für Skizzen die gegebenen Diagramme. Achten Sie darauf, die Achsen zu
beschriften.
Name:
1:
2:
Vorname:
3:
4:
5:
Punkte:
Note:
Musterlösung
Aufgabe 1 [4x4=16 Punkte].
(a)
clear all, close all, clc;
N = 16;
% Anzahl Punkte
n = 0:1:N-1;
x_n = cos(n*pi/8);
stem(n,x_n)
…
(b)
(c)
(d)
yc t  
t
 yb  d 
0
 
 exp 
 d 
 0
  
1
t
t

t
1 
    
   
    exp 
   1  exp 

 


 0 
   0

 
t 
  t 
yc t    exp     1  1  exp  
 
  

 
Endwert:
yc t  t   yc   1
1/6
Document1
SiSy, HS12, dqtm
Aufgabe 2
[5+3=8 Punkte].
(a) Mit Topologie-A kann man ein TPF realisieren.
Vergleich:
1
1
; 02 
;
LC
LC
 k 1
1
 LC  2  1012
0
k02 
 C
2d0  
1
RC
;
1
1
 4
 0,5 109  0,5nF
1
6
R  2d0  10  2 10 10
1012
1012
 L

 2 103  2mH
9
C
0,5 10
(b) Topologie-B implementiert ein BPF.
0dB/dec
Das Nenner von Topologie-B
ist gleich wie Topologie-A ,
aber der Zähler gibt eine
Asymptoten von +20dB/dek,
sodass das gesamte
Amplitudenspektrum sieht so
aus:
-40dB/dec
+20dB/dec
+20dB/dec
Aufgabe 3
[4+2=6 Punkte].
log(1/2d)
-20dB/dec
m t   B0  u t   A0  y t 


 y t   mt   A  y t 
1

(a) Von BSB herauslesen:
 t  ersetzen
Dann die 2te DGl einmal ableiten, und m
yt   m
 t   A1  y t 

yt   B0  ut   A0  yt   A1  y t 
yt   A1  y t   A0  yt   B0  ut 
DGl:
(b) Mit FT und die Ableitung-Eigenschaft:


Y  j    j   A1   j   A0  B0  U  j  ; G j  
2
Y  j 

U  j 
 j 
2
B0
 A1   j   A0

Oder alternative: mit Testsignal exp(jωt), und Ausgangssignal G(jω). exp(jωt) .
2/6
Document1
SiSy, HS12, dqtm
Aufgabe 4
(a)
[6+3=9 Punkte].
 y[0]  1  8  8
 y[1]  1  8  1  4  12

 y[2]  1  8  1  4  1  2  14
n

y[n]   g[k ]  u[n  k ]  y[3]  1  8  1  4  1  2  1 1  15
k  
 y[4]  1  4  1  2  1 1  7

 y[5]  1  2  1 1  3
 y[6]  1 1  1

Und alle andere y[n] = 0
(b) Ein Echo-Effekt wird erzeugt: Wiederholung der Audio-Sequenz mit zeitlichen
Verschiebungen und mit kleineren Amplituden (wegen Faltung mit verschobene DiracStösse mit abklingenden Amplituden).
3/6
Document1
SiSy, HS12, dqtm
Aufgabe 5
[3+4=7 Punkte].
xt   1 
(a)
3




 cos 2  15  t    1  cos 2  45  t  
2
2
2


(b)

 A0  1 oder A0  1 und

3


und 1  
 A1  
2
2



 A3  1 und  3   2
Notation-II:
Ak
2
*
ck  c k
ck 
Zusammenhang:
und

c  1  1  exp  j 
 0

3

3

c1    exp   j     j
4
2
4



1

1

c3    exp   j     j
2
2
2


Notation-III:
Aufgabe 6
for k  1 ;
phaseA0    0  
phaseck   k
for k  1
und
3
c 1  conjc1     j
4
und
1
c 3  conjc3     j
2
[3+2+3=8 Punkte].
(a)
Var-1 :
Var-2 :
N=50 ; fstep = Fs/N = 50kHz/50 = 1kHz
(wie Frequenzauflösung in Plot Var-1 fstep = 5kHz/5)
N=20 ; fstep = Fs/N = 50kHz/20 = 2,5kHz
(wie Frequenzauflösung in Plot Var-2 fstep = 5kHz/2 )
(b) Nein, sie würden nicht verfälscht, weil Fs > 2.Fmax (50kHz > 2.20kHz )
(c)
Bmk: Mehrere Lösungen möglich
z.Bsp:
fsig(1)
fsig(0)
10kHz
30kHz
30kHz
40kHz
20kHz
60kHz
Allgemeiner:
Anteil 10kHz kann auch sein: n.Fs ± 10kHz , z.Bsp.: 40kHz; 60kHz ; 90kHz ; 110kHz; …
Anteil 20kHz kann auch sein: n.Fs ± 20kHz , z.Bsp.: 30kHz; 70kHz ; 80kHz ; 120kHz; …
4/6
Document1
SiSy, HS12, dqtm
Aufgabe 7
[3+6=9 Punkte].
(a) Im Zeitbereich doppel so schnell (oder zweimal kürzer), bedeutet eine Bandbreite doppel
so gross wie das originale Filter, also fg = 2kHz.
Die entsprechende FT-Eigenschaft ist:
Zeit-Bandbreite Produkt oder Zeit-Skalierung oder Unschärfe-Relation.
yt   xa  t 
Time-Scaling or
Time-Bandwidth
Product
Y f 
1
f
 X 
a
a
(b) Durch die Multiplikation der Impulsantwort des Tiefpassfilters mit einem Cosinus
cos(2π.10k.f0.t) , bekommt man ein Bandpassfilter mit Zenterfrequenz fc=10kHz.
Die entsprechenden FT-Eigenschaften sind:
Frequency-Shift
oder
Convolution vs
Multiplication
yt   xt   e j 2 f 0t
Y  f   X  f  f0 
yt   x1 t   x2 t 
Y  f   X1 f   X 2  f 
y(t)
s(t)
Multiplizieren mit cosinus im
Zeitbereich ist äquivalent wie falten
mit Cosinus-Spektrum im
Frequenzbereich (und bewirkt eine
Frequenzverschiebung).
cos(2πf0·t)
S(f)
f

Cosinus-Spektrum
f
f0
-f0
Y(f)
f
f0
-f0
5/6
Document1
SiSy, HS12, dqtm
Aufgabe 8
[4+4=8 Punkte].
(a) Mit Anti-Imaging Filter: TPF 1te Ordnung
(b) Die Impulsantwort gZOH(t) ist wie das Referenz-Signal „square-pulse“ A.rect( t / τ)
(mit A=1 und tau = 2ms) , aber mit einer zeitlichen Verschiebung.
Diese Verschiebung hat nur Effekt bei dem Phasenspektrum (und keinen Effekt bei dem
Amplitudenspektrum). Also das Amplitudenspektrum ist gleich:
GZOH  f   A   sinc  f    1  sinc  f  
mit   0,002s
1
2
3
oder f  0,5kHz ;  1kHz ;  1,5kHz; ...
Die Nullstellen sind bei f   ;  ;  ; ...



6/6
Document1