Der Tunneleffekt beim Alpha

1
II.1 Alpha-Zerfall von Atomkernen
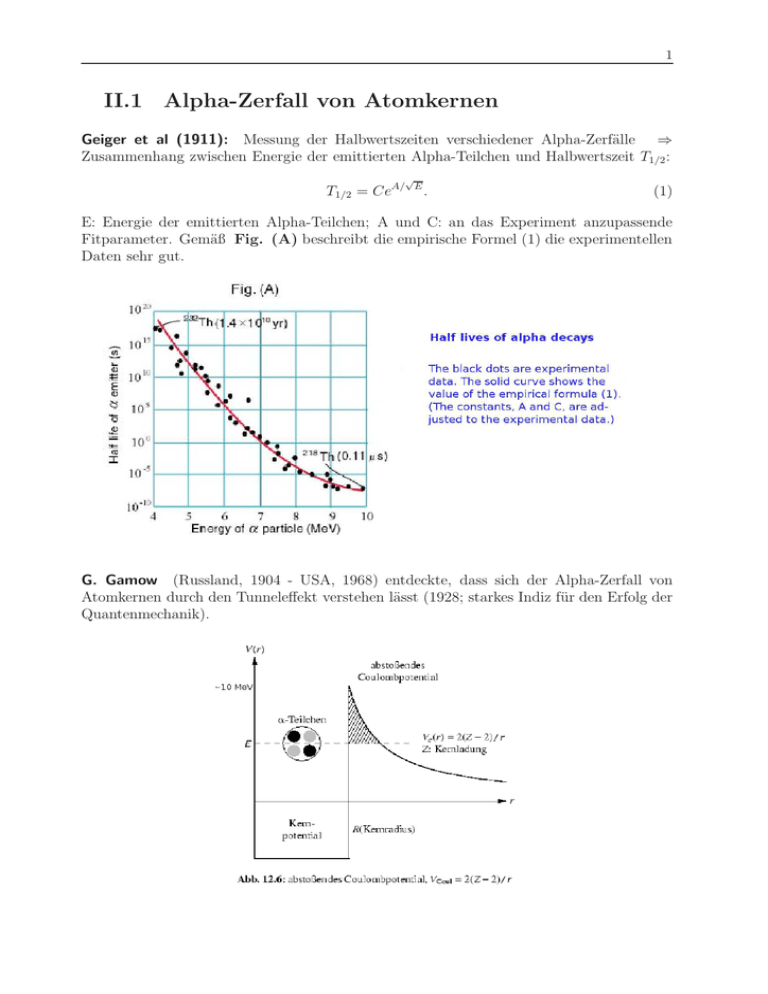
Geiger et al (1911): Messung der Halbwertszeiten verschiedener Alpha-Zerfälle ⇒
Zusammenhang zwischen Energie der emittierten Alpha-Teilchen und Halbwertszeit T1/2 :
√
T1/2 = CeA/
E
.
(1)
E: Energie der emittierten Alpha-Teilchen; A und C: an das Experiment anzupassende
Fitparameter. Gemäß Fig. (A) beschreibt die empirische Formel (1) die experimentellen
Daten sehr gut.
G. Gamow (Russland, 1904 - USA, 1968) entdeckte, dass sich der Alpha-Zerfall von
Atomkernen durch den Tunneleffekt verstehen lässt (1928; starkes Indiz für den Erfolg der
Quantenmechanik).
2
Tunnelwahrscheinlichkeit:
W (E) = exp −
bzw. allg.
W (E) =
n
Y
j=1
Z
b
R
Wj (E) = exp −
x1 = R (Kernradius), x2 = b =
2
h̄
2a q
2m(V0 − E) ≡ T (E),
h̄
2(Z−2)
E
|
Z
x2
x1
(2)
2q
2m(V (x) − E)dx ,
h̄ {z
}
(Gamow−F aktor)
(klassischer Umkehrpunkt,
2(Z−2)
b
= E).
s
Z
b
b
2√
dr 2m(Vc (r) − E) =
−1=
2mE
dr
h̄
r
R


s
s
2
R
2√
R
R
−
− 2 .
=
2mEb arccos
h̄
b
b
b
|
{z
}
√R
π
q
2

W (E) = exp −
2π √
h̄
(3)
−2
b

Z −2
−
2m  √
E
(4)
(5)
f uer b≫R
q
8R(Z − 2)
π


(6)
Die Halbwertszeit T1/2 des Kerns ist umgekehrt proportional zur Tunnelwahrscheinlichkeit (6):
1
v0
∝ W (E) wα ,
(7)
T1/2
2R
wobei wα ein Maß für die Wahrscheinlichkeit ist, ein Alphateilchen im Kern zu finden (dass
sich dort zwei Protonen und zwei Neutronen geeignet zusammenfinden, ist ja nicht eben
selbstverständlich), und v0 /(2R) die Anzahl der Stöße des Alphateilchens an die Coulombbarriere angibt (typische Geschwindigkeit des Alpha-Teilchens sei v0 ).
Aus der entscheidenden E −0.5 - Abhängigkeit in (6) folgt die Geiger-Nuttall-Regel:
1
log10 (T1/2 ) ∝ √ .
E
Anhand der Vorfaktoren in Gl.
unterscheiden.
(8)
(1) lassen sich verschiedene Zerfallsreihen