Exp.Funktionen mit negativer Hochzahl

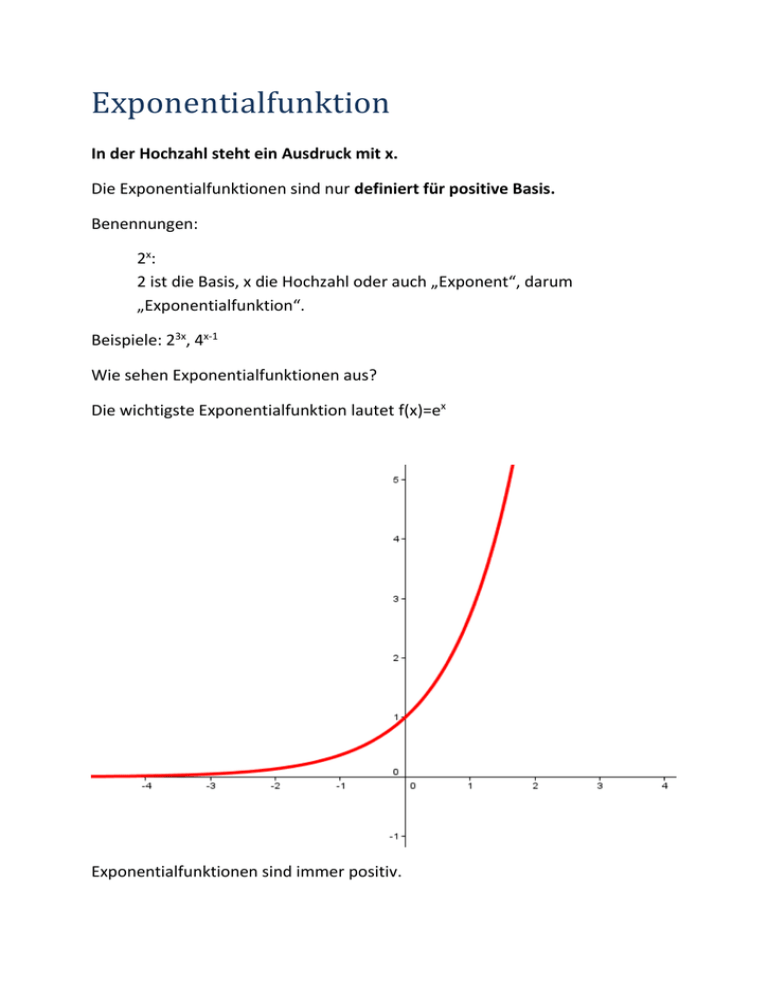
Exponentialfunktion
In der Hochzahl steht ein Ausdruck mit x.
Die Exponentialfunktionen sind nur definiert für positive Basis.
Benennungen:
2x:
2 ist die Basis, x die Hochzahl oder auch „Exponent“, darum
„Exponentialfunktion“.
Beispiele: 23x, 4x-1
Wie sehen Exponentialfunktionen aus?
Die wichtigste Exponentialfunktion lautet f(x)=ex
Exponentialfunktionen sind immer positiv.
An der Stelle x=1 kann man senkrecht nach oben gehen, schneidet man dort
die Exp.Funktion, so erhält man die Basis als y-Wert des Schnittpunktes.
Jede Exp.Funktion geht durch den Punkt (0,1).
Für positive x-Werte ist die Exp.Funktion mit der größeren Basis immer
größer,
Für negative x-Werte ist die Exp.Funktion mit der größeren Basis immer
kleiner.
„Verschobene“ Exp.Funktionen:
Beispiel: 4x-1 ( rot) im Vergleich zu 4x (blau):
4x-1 ist um 1 nach rechts verschoben im Vergleich zu 4x.
Wie sieht nun 4x-1 +2 aus (grün): um 2 nach oben verschoben:
Nun zu
Exp.Funktionen mit negativer Hochzahl:
4-x (schwarz) ist wie 4x, aber gespiegelt an der y-Achse:
2-x
Exp.Funktionen mit negativer Hochzahl werden verwendet als Modell bei
Abbau-Prozessen, Zerfallsprozessen und ähnlichen.
Exp.Funktionen mit positiver Hochzahl werden verwendet als Modell bei
Wachstumsprozessen.
Wie löst man das folgende Beispiel mit GeoGebra:
„Wann ist die Konzentration einer zerfallenden chemischen Substanz auf 40%
ihres Anfangswertes gefallen, wenn sie in 10 min auf die Hälfte des
Anfangswertes fällt?
Eingabe: f(x)=100 *(0.5)x/10 (100 entspricht 100%):
Der Schnittpunkt von y=40 mit f(x) ergibt den Punkt A.
Die x-Koordinate von A ergibt die Zeit, hier ca. 13,2 min.
Eine andere, häufig von PhysikerInnen gewählte Formel für die Berechnung von
Abbauprozessen lautet;
N (t )  N (0)  e
 ln(2 )t
T1 / 2
Erklärung:
N(t)…Anzahl oder Konzentration oder Radioaktivität… zur Zeit t
N(0)…Anzahl oder Konzentration oder Radioaktivität… zur Zeit t=0,
also am Beginn
T1/2…. Halbwertszeit für den Abbauprozess.
Der Ausdruck ln(2) ergibt sich aus der Umrechnung von 0.5x, (was man auch als
(1/2)x oder auch als 2-x schreiben kann(warum?)) auf e-x.
2-x =